2021-2022学年高一上学期数学人教B版(2019)必修第二册4.5增长速度的比较课件(17张ppt)
文档属性
| 名称 | 2021-2022学年高一上学期数学人教B版(2019)必修第二册4.5增长速度的比较课件(17张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-03 00:00:00 | ||
图片预览






文档简介
(共17张PPT)
增长速度的比较
学习目标
课标要求:
1.了解和体会函数模型在实际生活中的广泛应用.2.理解直线上升、指数爆炸、对数增长的含义以及三种函数模型性质的比较.(重点)3.会分析具体的实际问题,能够建模解决实际问题.(难点)
核心素养:
1.通过三种不同增长的函数模型差异的学习,培养逻辑推理的核心素养.2.借助函数模型的应用,提升数学建模的核心素养.
情境与问题
有一套房子,价格为200万元,假设房价每年上涨10%,某人每年固定能攒下40万元,如果他想买这套房子,在不贷款、收入不增加的前提下,这个人需要多少年才能攒够钱买这套房子?
A.5年 B.7年 C.8年
D.9年 E.永远也买不起
问题1:凭直觉,你认为上述问题的答案是什么?为什么?
问题2:房价的增长速度一直都比攒钱的增长速度快吗?
问题3:我们可以怎么刻画它们的增长速度呢?
平均变化率:
温故知新
一般地,当时, 称 为函数
在区间, ]( 时)或, ]( 时)上的
平均变化率.
也可以理解为:
自变量每增加1个单位,函数值平均将增加 个单位.
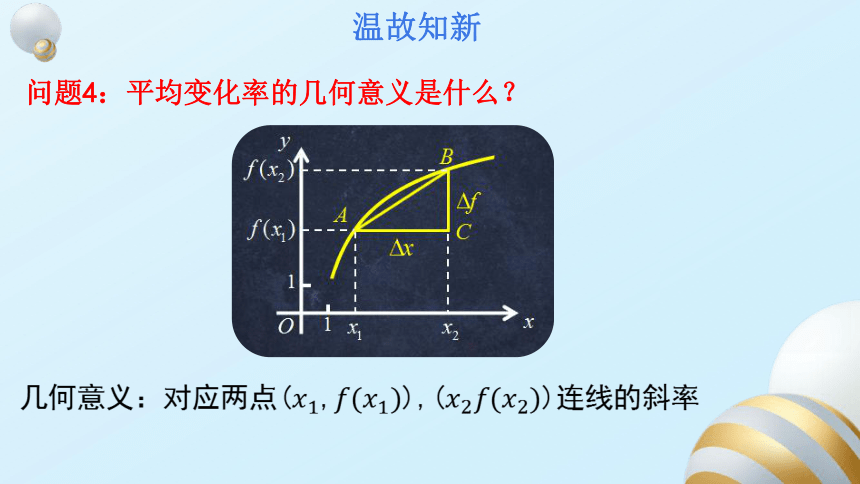
问题4:平均变化率的几何意义是什么?
温故知新
例1. 结合预习学案中求出的f(x)=2x+3,g(x)=3x-2,h(x)=x2-2x-1在区间[1,2]和[2,3]上的平均变化率,并说明,当自变量每增加1个单位时,函数值的变化规律.
典例探究
问题5:在区间[1,2]上,这三个函数平均变化率的大小关系如何?在区间[2,3]上呢?体现在图像上有什么特点?
反思感悟 素养提升
变式训练:
当,任取一个长度为1的区间[,
你能比较 , ,在此区间上的大小吗?
由此,我们能得出怎样的一般规律?
同一函数在不同区间上可能有不同的平均变化率.
反思感悟 素养提升
一次函数的平均变化率是常数;
不同函数在同一区间上可能有不同的平均变化率;
典例探究
反思感悟 素养提升
思考:
①用自己的语言描述这三个函数在区间(0,+∞)的增长趋势.
②结合函数图像,说明
的实际意义.
反思感悟 素养提升
思考3:
你能总结一下我们目前可以用函数进行拟合的增长模型吗?
线性增长:类似一次函数的增长
指数增长:类似指数函数的增长
对数增长:类似对数函数的增长
抛物线增长:类似二次函数的增长
反比例增长:类似反比例函数的增长
……
思考4:
你能举出生活中这些增长模型的例子吗?
回扣情境与问题
有一套房子,价格为200万元,假设房价每年上涨10%,某人每年固定能攒下40万元,如果他想买这套房子,在不贷款、收入不增加的前提下,这个人需要多少年才能攒够钱买这套房子?
A.5年 B.7年 C.8年 D.9年 E.永远也买不起
问题1:凭直觉,你认为上述问题的答案是什么?为什么?
问题2:房价的增长速度一直都比攒钱的增长速度快吗?
例3:我们再来研究本节课开始的问题:
回扣情境与问题
设经过x(x∈N)年后,房价为h(x)万元,这个人攒下的钱共有r(x) 万元,则这两个函数的解析式分别为:
, ,(x∈N) .
在区间 上,
令 ,得: ,所以 ,
即 a≥8时,房价的增长速度比攒钱的增长速度快.
回扣情境与问题
我们也可以列表,直观地看一看这两个函数值(取整数,单位:万元)的变化情况:
x 1 2 3 4 5 6 7 8 9
h(x) 220 242 266 293 322 354 390 429 472
r(x) 80 120 160 200 240 280 320 360 400
课堂小结
2. 函数的平均变化率刻画函数的增长速度的快慢;
3. 简单比较指数增长、线性增长、对数增长的增长速度.
1.数学建模思想:
实际问题
数学问题
平均变化率
当堂检测
作业布置
阅读课本第40页拓展阅读“指数运算与生活哲学”,
并举出一个生活中的指数增长的例子;
2.完成学案中【核心素养专练】(能力提升部分为选做题);
3.学有余力的同学思考:课本第41页习题4-5C第1、2题
增长速度的比较
学习目标
课标要求:
1.了解和体会函数模型在实际生活中的广泛应用.2.理解直线上升、指数爆炸、对数增长的含义以及三种函数模型性质的比较.(重点)3.会分析具体的实际问题,能够建模解决实际问题.(难点)
核心素养:
1.通过三种不同增长的函数模型差异的学习,培养逻辑推理的核心素养.2.借助函数模型的应用,提升数学建模的核心素养.
情境与问题
有一套房子,价格为200万元,假设房价每年上涨10%,某人每年固定能攒下40万元,如果他想买这套房子,在不贷款、收入不增加的前提下,这个人需要多少年才能攒够钱买这套房子?
A.5年 B.7年 C.8年
D.9年 E.永远也买不起
问题1:凭直觉,你认为上述问题的答案是什么?为什么?
问题2:房价的增长速度一直都比攒钱的增长速度快吗?
问题3:我们可以怎么刻画它们的增长速度呢?
平均变化率:
温故知新
一般地,当时, 称 为函数
在区间, ]( 时)或, ]( 时)上的
平均变化率.
也可以理解为:
自变量每增加1个单位,函数值平均将增加 个单位.
问题4:平均变化率的几何意义是什么?
温故知新
例1. 结合预习学案中求出的f(x)=2x+3,g(x)=3x-2,h(x)=x2-2x-1在区间[1,2]和[2,3]上的平均变化率,并说明,当自变量每增加1个单位时,函数值的变化规律.
典例探究
问题5:在区间[1,2]上,这三个函数平均变化率的大小关系如何?在区间[2,3]上呢?体现在图像上有什么特点?
反思感悟 素养提升
变式训练:
当,任取一个长度为1的区间[,
你能比较 , ,在此区间上的大小吗?
由此,我们能得出怎样的一般规律?
同一函数在不同区间上可能有不同的平均变化率.
反思感悟 素养提升
一次函数的平均变化率是常数;
不同函数在同一区间上可能有不同的平均变化率;
典例探究
反思感悟 素养提升
思考:
①用自己的语言描述这三个函数在区间(0,+∞)的增长趋势.
②结合函数图像,说明
的实际意义.
反思感悟 素养提升
思考3:
你能总结一下我们目前可以用函数进行拟合的增长模型吗?
线性增长:类似一次函数的增长
指数增长:类似指数函数的增长
对数增长:类似对数函数的增长
抛物线增长:类似二次函数的增长
反比例增长:类似反比例函数的增长
……
思考4:
你能举出生活中这些增长模型的例子吗?
回扣情境与问题
有一套房子,价格为200万元,假设房价每年上涨10%,某人每年固定能攒下40万元,如果他想买这套房子,在不贷款、收入不增加的前提下,这个人需要多少年才能攒够钱买这套房子?
A.5年 B.7年 C.8年 D.9年 E.永远也买不起
问题1:凭直觉,你认为上述问题的答案是什么?为什么?
问题2:房价的增长速度一直都比攒钱的增长速度快吗?
例3:我们再来研究本节课开始的问题:
回扣情境与问题
设经过x(x∈N)年后,房价为h(x)万元,这个人攒下的钱共有r(x) 万元,则这两个函数的解析式分别为:
, ,(x∈N) .
在区间 上,
令 ,得: ,所以 ,
即 a≥8时,房价的增长速度比攒钱的增长速度快.
回扣情境与问题
我们也可以列表,直观地看一看这两个函数值(取整数,单位:万元)的变化情况:
x 1 2 3 4 5 6 7 8 9
h(x) 220 242 266 293 322 354 390 429 472
r(x) 80 120 160 200 240 280 320 360 400
课堂小结
2. 函数的平均变化率刻画函数的增长速度的快慢;
3. 简单比较指数增长、线性增长、对数增长的增长速度.
1.数学建模思想:
实际问题
数学问题
平均变化率
当堂检测
作业布置
阅读课本第40页拓展阅读“指数运算与生活哲学”,
并举出一个生活中的指数增长的例子;
2.完成学案中【核心素养专练】(能力提升部分为选做题);
3.学有余力的同学思考:课本第41页习题4-5C第1、2题
