切线的判定和性质

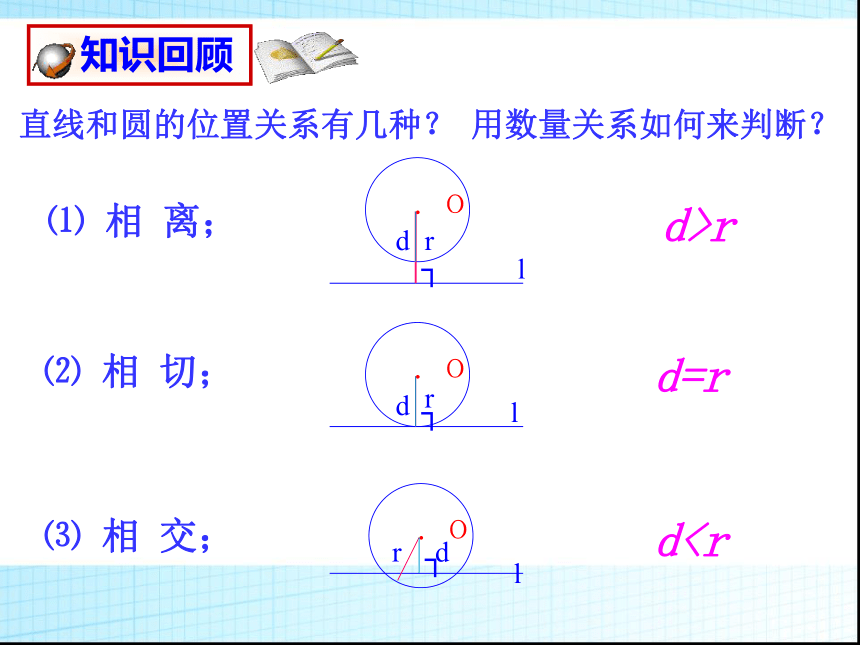
课件24张PPT。义务教育课程标准实验教科书九年级上册切线的判定和性质直线和圆的位置关系有几种？⑴ 相 离；⑵ 相 切；⑶ 相 交；dr用数量关系如何来判断？┐dr┐dr┐dr问题1：下雨天，转动的雨伞上的水滴是
顺着伞的什么方向飞出去的?问题2：砂轮转动时，火花是沿着砂轮的
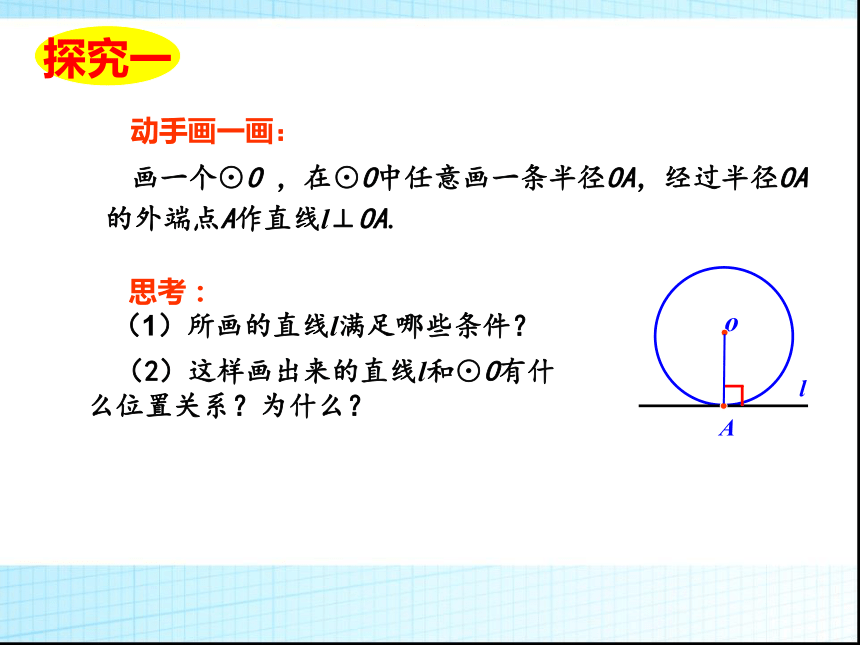
什么方向飞出去的? 动手画一画：
画一个⊙O ，在⊙O中任意画一条半径OA，经过半径OA的外端点A作直线l⊥OA.Alo 思考：
（1）所画的直线l满足哪些条件？ （2）这样画出来的直线l和⊙O有什
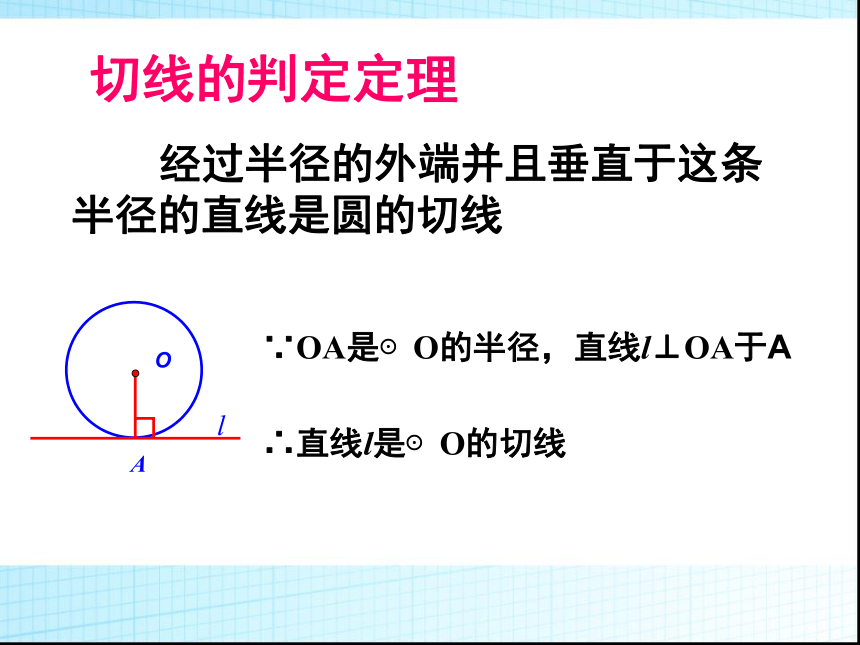
么位置关系？为什么？切线的判定定理 经过半径的外端并且垂直于这条半径的直线是圆的切线
∵OA是⊙O的半径，直线l⊥OA于A
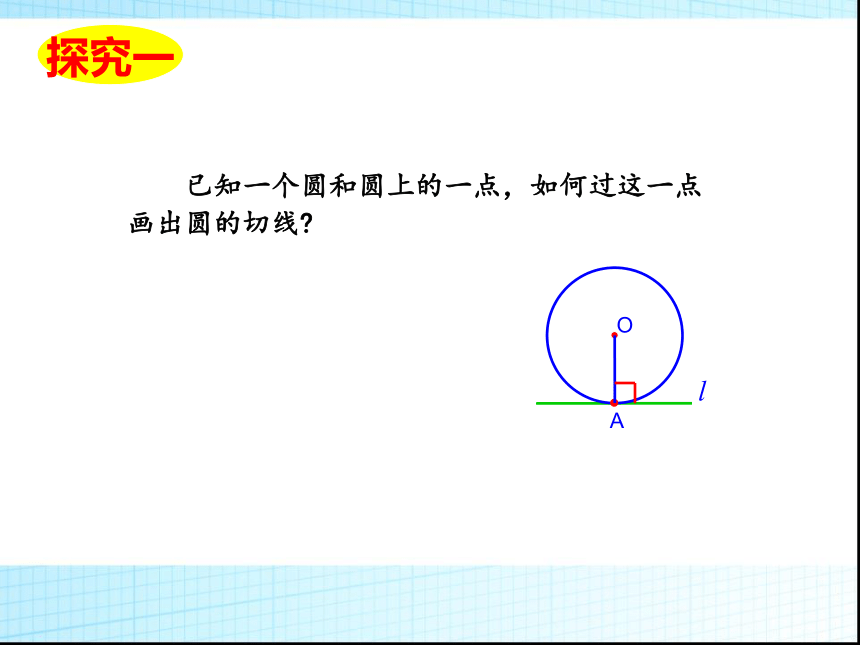
∴直线l是⊙O的切线lAO 已知一个圆和圆上的一点，如何过这一点
画出圆的切线?lAO生活中的问题
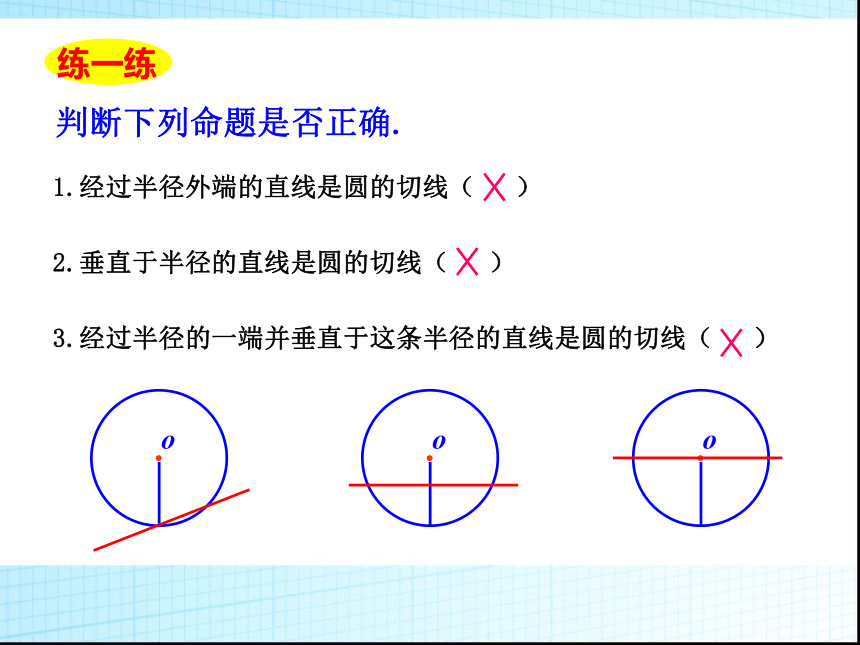
下雨天你快速的转动雨伞,转动的雨伞上的水滴是顺着伞的什么方向飞出的？砂轮转动时，火花是沿着砂轮的什么方向飞出去的？ 转动的雨伞上的水滴,砂轮转动时的火花都是沿着圆的切线的方向飞出去的。1.经过半径外端的直线是圆的切线（ ）
2.垂直于半径的直线是圆的切线（ ）
3.经过半径的一端并垂直于这条半径的直线是圆的切线（ ）
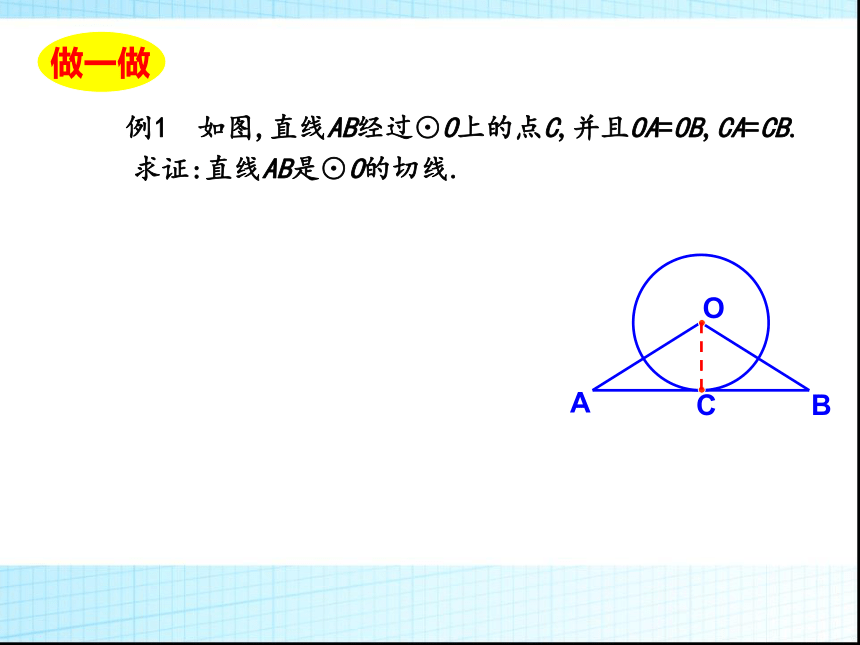
判断下列命题是否正确. 例1 如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB.
求证:直线AB是⊙O的切线. 例2、如右图所示，已知直线AB经过⊙O上的点A，且AB＝OA，∠OBA＝45°，直线AB是⊙O的切线吗？为什么？解：直线AB是⊙O的切线 。理由如下：AB1、以三角形的一边为直径的圆恰好与另一边相切，则此三角 形是__________三角形 直角2、如图，线段AB经过圆心O，交⊙O于点A、C，∠BAD＝∠B＝30°，边BD交圆于点D。BD是⊙O的切线吗？为什么？ 3、如右图所示，已知OC平分∠AOB，D是OC上任意一点，⊙D与OA相切于点E。那么，OB是⊙D的切线吗？请说明理由。 例1、如图，已知AB是⊙O的直径，点C在⊙O上，过点C 的直线与AB的延长线交于点P，∠ACO=∠PCB.
求证：PC是⊙O的切线.拓展应用 例2、如图△ABC中，AB=AC，以AB为直径的⊙O交BC于 P,PD⊥AC于D 求证：PD是⊙O的切线拓展应用学后反思利用切线的判定定理证明圆的切线的一般思路： 1、连接圆心和直线与圆的公共点。（常见辅助线）2、证明直线与已连的半径垂直。1.等腰△OAB中，OA=OB ，AB=10
（1）⊙O与AB相切于C点，则AC= .
（2）若C点是AB的中点，⊙O经过点C，
则⊙O与AB的位置关系是 . 5相切练一练探究新知 2、如图，l为⊙O的切线，A为切点，观察并猜想直线l与半径OA有怎样的位置关系?M定理：圆的切线垂直于过切点的半径证明:假设OA与l不垂直作OM⊥l,则OM 0A(r)即OM r∴ ⊙O与直线l相交这与已知相矛盾∴假设不成立∴ OA ⊥l＜＜切线的性质∵ 直线l是⊙O的切线，A为切点
∴直线l⊥OA圆的切线垂直于过切点的半径例2 如图，⊙O中，AB切⊙O于点C，且OA=OB.
求证：AC=CB.例1 如图,直线AB经过⊙O上的点C,并且OA=OB,CA=CB.
求证:直线AB是⊙O的切线.例2 如图，⊙O中，AB切⊙O于点C，且OA=OB.
求证：AC=CB.连半径 证垂直连半径 得垂直例3、已知AB是⊙O的直径，BC是⊙O的切线，切点为B，OC平行于弦AD
求证：DC是⊙O的切线1342证明：连接OD∵OA=OD∴ ∠1= ∠3又AD ∥ OC∴∠1= ∠2，∠3= ∠4∴ ∠2= ∠4
∵OD=OB,OC公共∴△OCD≌△OCB∴∠ODC= ∠ OBC∵BC与⊙O相切∴∠OBC=900∴OD⊥DC∴DC是⊙O的切线拓展应用二∴∠ODC=900 如图：AB为⊙O的直径，C为⊙O点．AD⊥CD,AC平 分∠DAB.
求证:CD是⊙O的切线.
变式练习
在上题中若将结论“CD是⊙O的切线”与条件“AC平分∠DAB”互换，其他条件不变,该如何证明. ADCBO善于总结是学习的前提条件1、如何判定一条直线是已知圆的切线？(1)只有一个公共点；(2) d=r(3)过半径外端且垂直于这条半径的直线是圆的切线；2、圆的切线有什么性质？（3）圆的切线垂直于经过切点的半径。(1)只有一个公共点；(2) d=r3、解决切线问题时如何添加辅助线呢？（1）若直线与圆公共点明确时： 连半径证垂直；
（2）若直线与圆公共点不确定时：作垂线证半径。
（3）若直线和圆相切于某个点时：连半径得垂直。布置作业
课本 第101页第4题
第103页第14题
相信自己
———有付出就有回报