2021-2022学年高一上学期物理人教版(2019)必修第一册2.4自由落体运动 知识点归纳+课堂检测(word版含答案)
文档属性
| 名称 | 2021-2022学年高一上学期物理人教版(2019)必修第一册2.4自由落体运动 知识点归纳+课堂检测(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 194.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-12-31 00:00:00 | ||
图片预览




文档简介
2 匀变速直线运动的研究
2.4 自由落体运动
一 自由落体运动
1自由落体运动的基本概念:
1、自由落体运动需满足两个条件: (1)初速度为零(2)只受重力
2、现在我们已经知道了自由落体运动的条件,思考一个问题,为什么在地球.上相同的高度处扔一一个铁球和一个羽毛,铁球先落地呢
我们从条件出发,两个物体都是初速度为零,但是羽毛除了受重力以外还受空气阻力,由于羽毛受到的空气阻力相对于自身重力而言是比较大的,因此不是自由落体运动,落地时间要长- -些。
3、物体自由下落时,忽略空气阻力,都可近似看做自由落体。自由落体运动同“光滑水平面”、“理想电流表”、“光线”等概念-一样,是一种理想化的模型。
2、自由落体运动的特点:
1、自由落体运动是否是初速度为零的匀加速直线运动呢 我们做个小实验即可证明。
利用间隔0.1s的频闪相机去拍摄一一个空中自由下落的小球,并将底片放在刻度尺上,读取每个影像间的距离,记作s1、 s2、 3...经计算可得As= aT2,因此自由落体运动确实是一个初速度为零的匀加速直线运动。
2、.上述实验中,a≈9.8m/s2。这个在本节课中叫做重力加速度,用g表示,即g≈9.8m/s2。 注意重力加速度g是个矢量,方向是竖直向下的。
3、重力加速度
地球上纬度不同的地方通常重力加速度的大小是不同的,如下表:
显然:纬度越高,对应的重力加速度越大;纬度越低,对应的重力加速度越小。
同时,重力加速度还跟高度有关:纬度相同的地方,高度越高,重力加速度越小。
重力加速度常取g=9.8m/s2,粗略计算时取g= 10m/s2。月球上的重力加速度只有地球表面的1/6, 约为1.6m/s2。
二 应用自由落体运动规律解题
1、自由落体运动规律
自由落体是初速为零的匀加速直线运动,匀变速直线运动的规律完全适用,不过需要简单的变形。
匀变速直线运动的规律如下:
vt= Vo+ at
在自由落体运动中,用g表示加速度,用h表示位移。又由于初速度v。=0,故自由落体运动规律可用下列公式表示:
三 自由落体运动规律的灵活应用
自由落体运动是初速度为零的匀加速直线运动,所以前面的比例法也满足自由落体运动;前面图像法和解析法证明了初速度为零的匀加速直线运动的各种比例;现在直接进行复习和归纳。
推论1:初速度为零的匀加速直线运动,通过连续相等的时间
(1)1t末、2t末、3t....瞬时速度之比:.
12....:n
(2) 1t末、2t末、3t ....位移之比:: .
1:4....:n2
(3)第1个t内、第2个t内、第3个t.....位移之比::
1.3.... (2n-1)
推论2:初速度为零的匀加速直线运动,通过连续相等的位移
(1) 1x内、2x内、3x内....时间之比:
(2) 1x末、2x末、3x 末..速度之比::
(3)第1个x内、第2个x内、第3个x内...时间之比:
1: (√2-1) ... (√n-√n- 1)
通过分析v-t图像、结合相似三角形中“两个相似三角形面积比等于相似比的平方”来理解记忆两组比例关系。
(2) 总结:比例法在解决自由落体运动时非常方便,所以要熟记各种情况下的比例以及对应条件,在做题目时出现从头开始等时间或等位移条件时可优先考虑比例的应用,再结合相应的公式解决整个问题。当然一些匀减速运动的题目也可运动逆向思维利用比例法解题。
四 测重力加速度
1测重力加速度的方法.
1、频闪照片法
(1)原理:相等时间间隔位移差
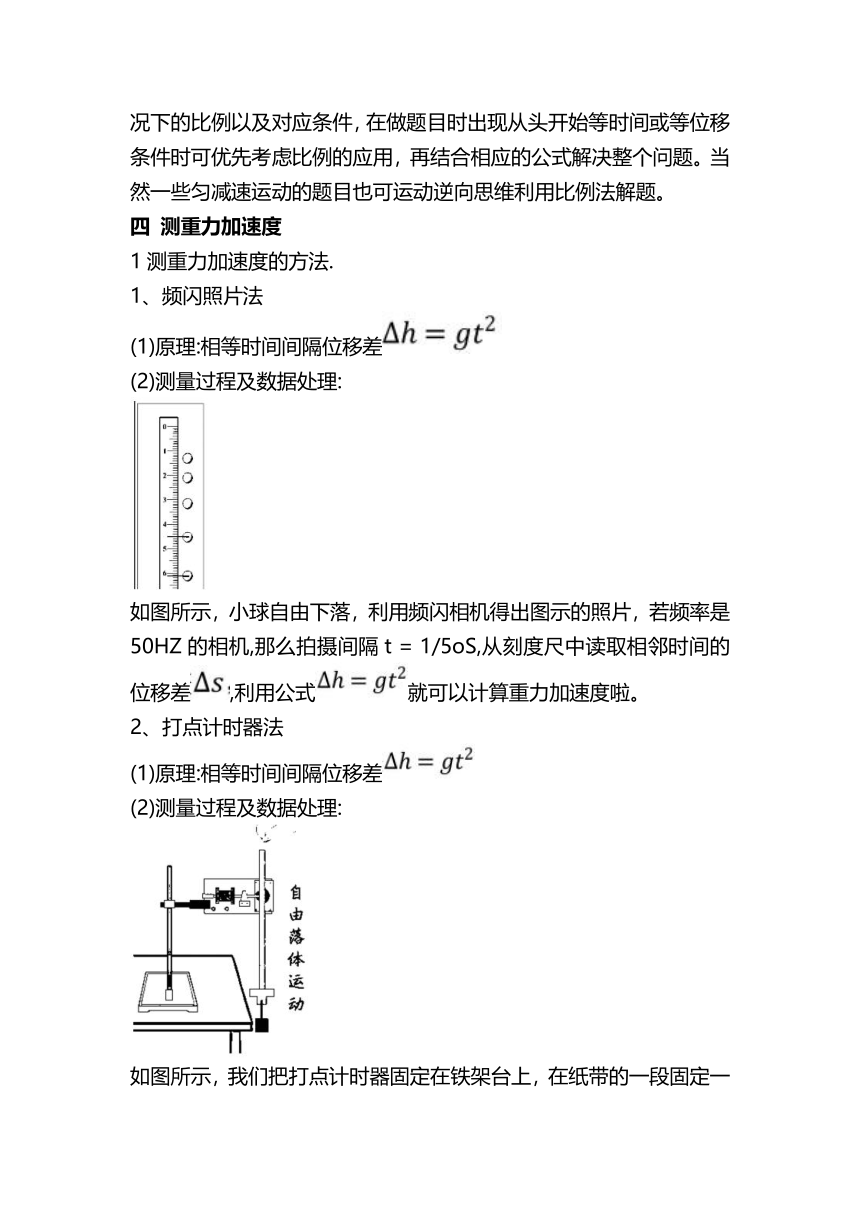
(2)测量过程及数据处理:
如图所示,小球自由下落,利用频闪相机得出图示的照片,若频率是50HZ的相机,那么拍摄间隔t = 1/5oS,从刻度尺中读取相邻时间的位移差,利用公式就可以计算重力加速度啦。
2、打点计时器法
(1)原理:相等时间间隔位移差
(2)测量过程及数据处理:
如图所示,我们把打点计时器固定在铁架台上,在纸带的一段固定一 个重物,让其自由下落,留下一条带有点的纸带。
若交流电频率是50HZ,那么两个点之间的时间间隔是t=5oS。根据纸带上的距离的测量数值,使用逐差法去计算g即可。
3、滴水法
(1)器材:刻度尺,秒表,可以滴水的水龙头,盘子。
(2)操作方法及数据处理:实验时仔细调整水龙头的阀门,在第一滴 水刚落入盘中听到响声的瞬间,让第二滴水正好从管口落下,这样两次响声之间的时间,就是水滴下落的时间。为了保证测量的准确性,我们测量第一声到第n声的总时间t点,这就是(n- 1)滴水下落的时间,所以一个水滴下落的时间就是,再利用刻度尺测出水龙头离盘子的距离h,利用公式h =1/ 2gt就可以计算重力加速度了。
2、关于三个方法的使用说明
方法一和方法二对于匀变速直线运动都是通用的,而方法三是专门用来测量自由落体的,因此局限性比较大。同学们在学习的过程中,对这几个方法要熟练的掌握。
课堂检测
1如图所示,在足够高的空间内,小球位于空心管的正上方h处,空心管长为L,小球球心与管的轴线重合,并在竖直线上。当释放小球,小球可能穿过空心管,不计空气阻力,则下列判断正确的是( )
A两者同时无初速度释放,小球不能穿过管
B两者同时释放,小球具有竖直向下的初速度v0,管无初速度,则小球一定能穿过管,且穿过管的时间与当地重力加速度有关
C两者同时释放,小球具有竖直向下的初速度v0,管无初速度,则小球一定能穿过管,但穿过管的时间与当地重力加速度无关
D两者均无初速度释放,但小球提前了时间释放,则小球一定能穿过管,但穿过管的时间与当地重力加速度无关
2 关于自由落体运动,下列说法正确的是( )
A不考虑空气阻力的运动就是自由落体运动
B做自由落体运动的物体不受任何外力
C做自由落体运动的物体,从静止开始在连续相等的时间间隔内位移比是1:3:5…:(2n﹣1)
D在同一地点,质量不同的物体做自由落体运动的加速度相同
3 下列图象中,能反映自由落体运动规律的是( )
A
B
C
D
4 在同一地点,质量不同的两个物体从同一高度同时开始做自由落体运动,则( )
A质量大的物体下落的加速度大
B质量大的物体先落地
C质量小的物体先落地
D两个物体同时落地
5 甲、乙两物体质量之比为=5:1,甲从高H处自由落下的同时乙从2H处自由落下,不计空气阻力,以下说法错误的是( )
A在下落过程中,同一时刻二者速度相等
B甲落地时,乙距地面的高度为H
C甲落地时,乙的速度的大小为√2gH
D甲、乙在空中运动的时间之比为1:2
6 一个物体从45m高的地方静止释放,做自由落体运动(g取10m/s2),则物体到达地面时的速度为___1___m/s,物体下落的时间为___2___s,物体下落最后1s内的位移为___3___m.
7 一竖直的墙壁上AE被分成四个相等的部分,一物体由A点从静止释放做自由落体运动,如图所示,下列结论正确的是( )
A物体到达各点的速率vB vC vD vE=1:2:3:4
B物体通过每一部分时,其速度增量vB﹣vA=vC﹣vB=vD﹣vC=vE﹣vD
C物体从A到E的平均速度 v=vB
D物体从A到E的平均速度 v=vC
8由于当年实验条件的限制,伽利略无法直接对落体运动进行实验研究,但在今天我们可通过频闪照相的方式直接对自由落体进行研究.如图是某次实验拍摄的小球下落频闪照片的一部分,频闪间隔是130s.不同时刻小球的位置和相邻两时刻小球位移已标注图中,单位是cm,计算结果均保留三位有效数字. (1)根据此照片可以判断小球做匀变速直线运动,其依据为:小球在连续相等时间内的位移之差___1___(选填:“增大”、“减小”或“相等”) (2)小球下落的加速度大小为___2___m/s2;(计算结果保留2位小数) (3)小球在2.18cm位置处的速度大小为___3___m/s.(计算结果保留3位有效数字)
参考答案
1解:A、若两者无初速度同时释放,则在相同时间内下降的高度相同,可知小球在空中不能穿过管,故A正确。 BC、两者同时释放,小球具有向下的初速度,管无初速度,根据Δx=v0t+12gt2 12gt2=v0t=h+L知,经过t=h+Lv0,小球穿过管,穿过管的时间与当地重力加速度无关,故B错误,C正确。 D、两者均无初速度释放,但小球提前了t时间释放,根据x=12g(t+Δt)2 12gt2=12gΔt2+gtΔt=h+L.可知小球能穿过管,穿过管的时间与当地的重力加速度有关。故D错误。 故选:AC。
2 解:A、自由落体运动是初速度为零的匀加速直线运动。故A错误。 B、做自由落体运动的物体只受到重力,故B错误; C、做自由落体运动的物体,在时间t内通过的位移h=12gt2,故前ts,前2ts,前3ts内通过的位移之比为1:4:5:…:n2,从静止开始在连续相等的时间间隔内位移比是1:3:5…:(2n﹣1),故C正确 D、在同一地点,质量不同的物体做自由落体运动的加速度相同,故D正确 故选:CD
3 解:AB、自由落体运动的加速度不变,做初速度为零的匀变速直线运动,根据s=12gt2知,位移与时间既不是成正比关系,也不是保持不变,故AB错误. CD、根据v=gt,知速度随时间成正比,由于竖直向下为正方向,所以速度为正值,故D正确,C错误. 故选:D
4 解:根据自由落体运动的公式h=12gt2,t=√2hg,知落地时间与质量无关,所以两个物体同时落地.故D正确,A、B、C错误. 故选D.
5 解:A、因为甲乙物体同时做自由落体运动,它们的初速度为零,加速度为g,任意时刻的速度为:v=gt,所以两物体下落过程中,在同一时刻甲的速度与乙的速度相等,故A正确。 B、甲落地时,甲乙运动的位移都为H,所以乙离地面的高度为:2H﹣H=H,故B正确; C、甲落地时,由位移速度关系式:v2=2gH,可得v=√2gH,它们的速度相同,故C正确; D、因为甲乙物体均做自由落体运动,加速度为g,甲下落的时间为√2Hg,乙下落的时间为√4Hg,所以甲、乙在空中运动的时间之比为1:√2,故D错误。 本题选错误的 故选:D
6 解:物体做自由落体运动,已知位移,根据位移时间关系公式,有h=1/2gt2 解得t=√2hg=√2×4510s=3s 根据速度时间关系公式,有 v=gt=10×3=30m/s 前2s的位移h1=12gt12=12×10×4=20m 故第3s的位移为h2h2=h﹣h1=45﹣20=25m 故答案为:30m/s,3s,25m.
7解:A、根据运动学公式v2v2﹣v02v02=2ax得:物体由A点从静止释放,所以v2=2ax,所以物体到达各点的速率之比vB vC vD vE=1 √2 √3 √4,故A错误;
B、物体做加速运动,物体通过每一部分时,所用时间逐渐减少,故速度增量逐渐减小,故B错误;
C、根据自由落体运动的前两段相等时间内的位移比为1:3.故下落到B点时的时间为总时间的一半,由中间时刻的瞬时速度等于此段时间的平均速度可知,C正确;
D、由C知,故D错误. 故选:C.
8 解:(1)因为连续相等时间内的位移之差为一恒量,可知小球做匀变速直线运动.
(2)由图可知,在连续相等时间内的位移之差△x=1.09cm,根据△x=aT2得,加速度g=(h3+h4) (h1+h2)4T2=((4.90+3.81) (1.64+2.72))×10 24×1900m/s2≈9.79m/s2.
(3)小球在2.18cm位置处的速度大小v=(1.64+2.72)×10 22×130m/s=0.654m/s. 故答案为:(1)相等(2)9.79,(3)0.654.
2.4 自由落体运动
一 自由落体运动
1自由落体运动的基本概念:
1、自由落体运动需满足两个条件: (1)初速度为零(2)只受重力
2、现在我们已经知道了自由落体运动的条件,思考一个问题,为什么在地球.上相同的高度处扔一一个铁球和一个羽毛,铁球先落地呢
我们从条件出发,两个物体都是初速度为零,但是羽毛除了受重力以外还受空气阻力,由于羽毛受到的空气阻力相对于自身重力而言是比较大的,因此不是自由落体运动,落地时间要长- -些。
3、物体自由下落时,忽略空气阻力,都可近似看做自由落体。自由落体运动同“光滑水平面”、“理想电流表”、“光线”等概念-一样,是一种理想化的模型。
2、自由落体运动的特点:
1、自由落体运动是否是初速度为零的匀加速直线运动呢 我们做个小实验即可证明。
利用间隔0.1s的频闪相机去拍摄一一个空中自由下落的小球,并将底片放在刻度尺上,读取每个影像间的距离,记作s1、 s2、 3...经计算可得As= aT2,因此自由落体运动确实是一个初速度为零的匀加速直线运动。
2、.上述实验中,a≈9.8m/s2。这个在本节课中叫做重力加速度,用g表示,即g≈9.8m/s2。 注意重力加速度g是个矢量,方向是竖直向下的。
3、重力加速度
地球上纬度不同的地方通常重力加速度的大小是不同的,如下表:
显然:纬度越高,对应的重力加速度越大;纬度越低,对应的重力加速度越小。
同时,重力加速度还跟高度有关:纬度相同的地方,高度越高,重力加速度越小。
重力加速度常取g=9.8m/s2,粗略计算时取g= 10m/s2。月球上的重力加速度只有地球表面的1/6, 约为1.6m/s2。
二 应用自由落体运动规律解题
1、自由落体运动规律
自由落体是初速为零的匀加速直线运动,匀变速直线运动的规律完全适用,不过需要简单的变形。
匀变速直线运动的规律如下:
vt= Vo+ at
在自由落体运动中,用g表示加速度,用h表示位移。又由于初速度v。=0,故自由落体运动规律可用下列公式表示:
三 自由落体运动规律的灵活应用
自由落体运动是初速度为零的匀加速直线运动,所以前面的比例法也满足自由落体运动;前面图像法和解析法证明了初速度为零的匀加速直线运动的各种比例;现在直接进行复习和归纳。
推论1:初速度为零的匀加速直线运动,通过连续相等的时间
(1)1t末、2t末、3t....瞬时速度之比:.
12....:n
(2) 1t末、2t末、3t ....位移之比:: .
1:4....:n2
(3)第1个t内、第2个t内、第3个t.....位移之比::
1.3.... (2n-1)
推论2:初速度为零的匀加速直线运动,通过连续相等的位移
(1) 1x内、2x内、3x内....时间之比:
(2) 1x末、2x末、3x 末..速度之比::
(3)第1个x内、第2个x内、第3个x内...时间之比:
1: (√2-1) ... (√n-√n- 1)
通过分析v-t图像、结合相似三角形中“两个相似三角形面积比等于相似比的平方”来理解记忆两组比例关系。
(2) 总结:比例法在解决自由落体运动时非常方便,所以要熟记各种情况下的比例以及对应条件,在做题目时出现从头开始等时间或等位移条件时可优先考虑比例的应用,再结合相应的公式解决整个问题。当然一些匀减速运动的题目也可运动逆向思维利用比例法解题。
四 测重力加速度
1测重力加速度的方法.
1、频闪照片法
(1)原理:相等时间间隔位移差
(2)测量过程及数据处理:
如图所示,小球自由下落,利用频闪相机得出图示的照片,若频率是50HZ的相机,那么拍摄间隔t = 1/5oS,从刻度尺中读取相邻时间的位移差,利用公式就可以计算重力加速度啦。
2、打点计时器法
(1)原理:相等时间间隔位移差
(2)测量过程及数据处理:
如图所示,我们把打点计时器固定在铁架台上,在纸带的一段固定一 个重物,让其自由下落,留下一条带有点的纸带。
若交流电频率是50HZ,那么两个点之间的时间间隔是t=5oS。根据纸带上的距离的测量数值,使用逐差法去计算g即可。
3、滴水法
(1)器材:刻度尺,秒表,可以滴水的水龙头,盘子。
(2)操作方法及数据处理:实验时仔细调整水龙头的阀门,在第一滴 水刚落入盘中听到响声的瞬间,让第二滴水正好从管口落下,这样两次响声之间的时间,就是水滴下落的时间。为了保证测量的准确性,我们测量第一声到第n声的总时间t点,这就是(n- 1)滴水下落的时间,所以一个水滴下落的时间就是,再利用刻度尺测出水龙头离盘子的距离h,利用公式h =1/ 2gt就可以计算重力加速度了。
2、关于三个方法的使用说明
方法一和方法二对于匀变速直线运动都是通用的,而方法三是专门用来测量自由落体的,因此局限性比较大。同学们在学习的过程中,对这几个方法要熟练的掌握。
课堂检测
1如图所示,在足够高的空间内,小球位于空心管的正上方h处,空心管长为L,小球球心与管的轴线重合,并在竖直线上。当释放小球,小球可能穿过空心管,不计空气阻力,则下列判断正确的是( )
A两者同时无初速度释放,小球不能穿过管
B两者同时释放,小球具有竖直向下的初速度v0,管无初速度,则小球一定能穿过管,且穿过管的时间与当地重力加速度有关
C两者同时释放,小球具有竖直向下的初速度v0,管无初速度,则小球一定能穿过管,但穿过管的时间与当地重力加速度无关
D两者均无初速度释放,但小球提前了时间释放,则小球一定能穿过管,但穿过管的时间与当地重力加速度无关
2 关于自由落体运动,下列说法正确的是( )
A不考虑空气阻力的运动就是自由落体运动
B做自由落体运动的物体不受任何外力
C做自由落体运动的物体,从静止开始在连续相等的时间间隔内位移比是1:3:5…:(2n﹣1)
D在同一地点,质量不同的物体做自由落体运动的加速度相同
3 下列图象中,能反映自由落体运动规律的是( )
A
B
C
D
4 在同一地点,质量不同的两个物体从同一高度同时开始做自由落体运动,则( )
A质量大的物体下落的加速度大
B质量大的物体先落地
C质量小的物体先落地
D两个物体同时落地
5 甲、乙两物体质量之比为=5:1,甲从高H处自由落下的同时乙从2H处自由落下,不计空气阻力,以下说法错误的是( )
A在下落过程中,同一时刻二者速度相等
B甲落地时,乙距地面的高度为H
C甲落地时,乙的速度的大小为√2gH
D甲、乙在空中运动的时间之比为1:2
6 一个物体从45m高的地方静止释放,做自由落体运动(g取10m/s2),则物体到达地面时的速度为___1___m/s,物体下落的时间为___2___s,物体下落最后1s内的位移为___3___m.
7 一竖直的墙壁上AE被分成四个相等的部分,一物体由A点从静止释放做自由落体运动,如图所示,下列结论正确的是( )
A物体到达各点的速率vB vC vD vE=1:2:3:4
B物体通过每一部分时,其速度增量vB﹣vA=vC﹣vB=vD﹣vC=vE﹣vD
C物体从A到E的平均速度 v=vB
D物体从A到E的平均速度 v=vC
8由于当年实验条件的限制,伽利略无法直接对落体运动进行实验研究,但在今天我们可通过频闪照相的方式直接对自由落体进行研究.如图是某次实验拍摄的小球下落频闪照片的一部分,频闪间隔是130s.不同时刻小球的位置和相邻两时刻小球位移已标注图中,单位是cm,计算结果均保留三位有效数字. (1)根据此照片可以判断小球做匀变速直线运动,其依据为:小球在连续相等时间内的位移之差___1___(选填:“增大”、“减小”或“相等”) (2)小球下落的加速度大小为___2___m/s2;(计算结果保留2位小数) (3)小球在2.18cm位置处的速度大小为___3___m/s.(计算结果保留3位有效数字)
参考答案
1解:A、若两者无初速度同时释放,则在相同时间内下降的高度相同,可知小球在空中不能穿过管,故A正确。 BC、两者同时释放,小球具有向下的初速度,管无初速度,根据Δx=v0t+12gt2 12gt2=v0t=h+L知,经过t=h+Lv0,小球穿过管,穿过管的时间与当地重力加速度无关,故B错误,C正确。 D、两者均无初速度释放,但小球提前了t时间释放,根据x=12g(t+Δt)2 12gt2=12gΔt2+gtΔt=h+L.可知小球能穿过管,穿过管的时间与当地的重力加速度有关。故D错误。 故选:AC。
2 解:A、自由落体运动是初速度为零的匀加速直线运动。故A错误。 B、做自由落体运动的物体只受到重力,故B错误; C、做自由落体运动的物体,在时间t内通过的位移h=12gt2,故前ts,前2ts,前3ts内通过的位移之比为1:4:5:…:n2,从静止开始在连续相等的时间间隔内位移比是1:3:5…:(2n﹣1),故C正确 D、在同一地点,质量不同的物体做自由落体运动的加速度相同,故D正确 故选:CD
3 解:AB、自由落体运动的加速度不变,做初速度为零的匀变速直线运动,根据s=12gt2知,位移与时间既不是成正比关系,也不是保持不变,故AB错误. CD、根据v=gt,知速度随时间成正比,由于竖直向下为正方向,所以速度为正值,故D正确,C错误. 故选:D
4 解:根据自由落体运动的公式h=12gt2,t=√2hg,知落地时间与质量无关,所以两个物体同时落地.故D正确,A、B、C错误. 故选D.
5 解:A、因为甲乙物体同时做自由落体运动,它们的初速度为零,加速度为g,任意时刻的速度为:v=gt,所以两物体下落过程中,在同一时刻甲的速度与乙的速度相等,故A正确。 B、甲落地时,甲乙运动的位移都为H,所以乙离地面的高度为:2H﹣H=H,故B正确; C、甲落地时,由位移速度关系式:v2=2gH,可得v=√2gH,它们的速度相同,故C正确; D、因为甲乙物体均做自由落体运动,加速度为g,甲下落的时间为√2Hg,乙下落的时间为√4Hg,所以甲、乙在空中运动的时间之比为1:√2,故D错误。 本题选错误的 故选:D
6 解:物体做自由落体运动,已知位移,根据位移时间关系公式,有h=1/2gt2 解得t=√2hg=√2×4510s=3s 根据速度时间关系公式,有 v=gt=10×3=30m/s 前2s的位移h1=12gt12=12×10×4=20m 故第3s的位移为h2h2=h﹣h1=45﹣20=25m 故答案为:30m/s,3s,25m.
7解:A、根据运动学公式v2v2﹣v02v02=2ax得:物体由A点从静止释放,所以v2=2ax,所以物体到达各点的速率之比vB vC vD vE=1 √2 √3 √4,故A错误;
B、物体做加速运动,物体通过每一部分时,所用时间逐渐减少,故速度增量逐渐减小,故B错误;
C、根据自由落体运动的前两段相等时间内的位移比为1:3.故下落到B点时的时间为总时间的一半,由中间时刻的瞬时速度等于此段时间的平均速度可知,C正确;
D、由C知,故D错误. 故选:C.
8 解:(1)因为连续相等时间内的位移之差为一恒量,可知小球做匀变速直线运动.
(2)由图可知,在连续相等时间内的位移之差△x=1.09cm,根据△x=aT2得,加速度g=(h3+h4) (h1+h2)4T2=((4.90+3.81) (1.64+2.72))×10 24×1900m/s2≈9.79m/s2.
(3)小球在2.18cm位置处的速度大小v=(1.64+2.72)×10 22×130m/s=0.654m/s. 故答案为:(1)相等(2)9.79,(3)0.654.
