【培优讲义】第11讲:圆的周长、面积 答案版
文档属性
| 名称 | 【培优讲义】第11讲:圆的周长、面积 答案版 |

|
|
| 格式 | docx | ||
| 文件大小 | 778.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-31 16:50:04 | ||
图片预览



文档简介
答案版
第11讲:圆的周长与面积
教学目标
1、掌握圆的面积计算公式及应用;
2、掌握圆环面积公式及应用;
3、掌握圆的周长、面积与四边形的关系;
4、圆各部分与圆周长、圆面积的关系。
教学重难点
1、掌握圆的面积与圆环的面积;
2、掌握圆的周长、面积与四边形的关系;
3、圆各部分与圆周长、圆面积的关系。
三、教学过程
课堂回顾
讲评第11讲课后习题
(二)精讲精练
知识点1:圆的面积公式
圆的面积公式的推导:
把一个圆分成若干(偶数)等份,拼成一个近似的长方形,如果分成的分数越多,每一份就会越少,拼成的图形就会越接近长方形。这个长方形的长相当于圆的( 周长的一半 ),宽相当于圆的( 半径 ),公式( )。
例1:请把下面的表格填完整。
半径(r) 直径(d) 圆的周长(c) 圆的面积(s)
0.5m 1m 3.14 0.785
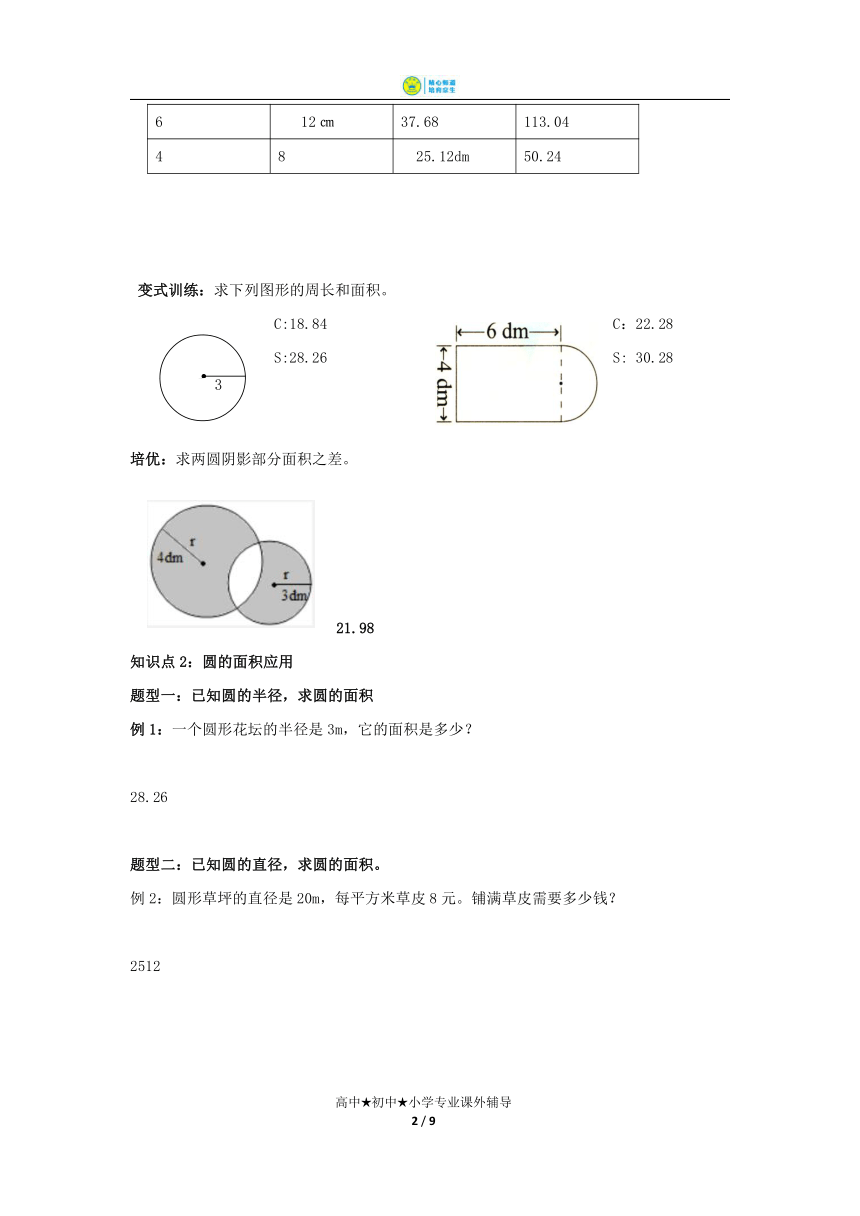
6 12㎝ 37.68 113.04
4 8 25.12dm 50.24
变式训练:求下列图形的周长和面积。
C:18.84 C:22.28
S:28.26 S: 30.28
培优:求两圆阴影部分面积之差。
21.98
知识点2:圆的面积应用
题型一:已知圆的半径,求圆的面积
例1:一个圆形花坛的半径是3m,它的面积是多少?
28.26
题型二:已知圆的直径,求圆的面积。
例2:圆形草坪的直径是20m,每平方米草皮8元。铺满草皮需要多少钱?
2512
题型三:已知圆的周长,求圆的面积
例3:一个圆形蓄水池的周长是25.12m,它的占地面积是多少平方米?
50.24
变式训练:
1. 草地的木桩上拴着一头牛,绳长4米,这头牛能够吃到草的最大面积是多少平方米?
50.24
2.一个运动场(如右图),两端是半圆形,中间是长方形。
沿着这个运动场跑1圈,要跑多少米?
388.4
给这个运动场铺上草坪,一共要铺草坪多少平方米?
8826
3. 把一张长6dm,宽4dm的纸剪成一个最大的圆,剩下部分的面积是多少平方分米?
11.44
知识点3:圆环面积公式
圆环外半径是R,内半径是r,外面大圆的面积是:3.14×R×R,
里面小圆的面积是:3.14×r×r,
圆环面积=大圆面积-小圆面积=3.14×R×R-3.14×r×r=3.14×(R -r )
例1:求出圆环面积。(单位:㎝)
87.92
例2: 在一个直径是16米的圆形喷水池周围铺设一条3米宽的水泥路,这条水泥路的面积是多少平方米?
178.98
变式训练:一块环形铁皮,外圆直径是1.6m,环宽是0.1m.这块铁皮的面积是多少平方厘米?
0.471
培优:
已知阴影部分的面积是5cm ,求圆环的面积。
31.4
知识点4、四边形与圆的关系
在正方形内画最大的圆,圆的直径就等于正方形的边长;在长方形内画一个最大的圆,圆的直径就是长方形的宽;在圆内画出一个最大正方形,圆的直径就等于正方形的对角线。
例1:试在正方形内画出最大的圆,在圆内画出最大的正方形。
2、在一个边长6分米的正方形里剪下一个最大的圆,剩下部分的面积( 7.74 )平方厘米。
变式训练:
1、如右图,圆的周长是( 6.28 )dm,长方形的周长是( 10 )dm。
2、如右图,正方形的周长是4cm,圆的周长是( C )cm。
A.4π B.2π C.π D.π
一张长方形的纸,长是18㎝,宽是12㎝。用这张长方形纸剪一个最大的圆,这个圆的半径多少㎝,周长多少㎝? 6 37.68
4、在一个长20厘米,宽10厘米的长方形纸片里减去一个最大的圆,剩下部分的面积是多少平方厘米。121.5
培优:
1.如下图,已知正方形的面积是20平方厘米,求圆的面积。
62.8
2. 求出下面图中阴影部分的面积。
7.74
知识点5、圆各部分与圆周长、圆面积的关系
圆的半径扩大为原来的几倍,直径、周长也扩大为原来的几倍;面积扩大为原来的平方倍。
例1、判断题:
(1)半径2米的圆,它的周长和面积相等。 ( × )
(2)圆的直径扩大到原来的6倍,它的面积就会扩大到原来的36倍。( √ )
(3)两个圆周长的比一定等于它们面积的比。 ( × )
变式训练:
1、小圆的直径等于大圆的半径,小圆的面积与大圆面积的是( B )。
A. 1∶2 B. 1∶4 C.1∶8
2、如右图,大圆O1和小圆O2面积的比是( B )
A.1:2 B. 1:4
C.2:1 D.4:1
3、如右图,圆面积与正方形面积的比是( C )
π:2 B.2:π C.π:4 D.4:π
培优:
1、如下图所示,两个小圆的周长之和与大圆的周长相比,谁长一些?请说明理由。
一样长
2、一根铁丝分别围成一个长方形、正方形、圆形,( C )的面积最大。
A.长方形 B.正方形 C.圆形 D.不能确定
课堂小测
一.填空
1.把一根6.28米长的铁丝围成一个正方形,则正方形的面积是( 2.4649 )平方米;若围成一个圆,则圆的面积是( 3.14 )平方米。
2.甲圆的半径是乙圆半径的2倍,那么,甲圆的直径是乙圆直径的( 2 )倍,甲圆的周长是乙圆周长的( 2 )倍,甲圆的面积是乙圆面积的( 4 )倍。
3.大圆周长是小圆周长的3倍,大圆面积是小圆面积的( 9 )倍。
4.一个半圆塑料板,半径是1分米,它的周长是( 5.14 )分米。
5.小圆半径是大圆半径的,那么小圆直径是大圆直径的,小圆周长是大圆周长的,小圆面积是大圆面积的。
6.一个圆的半径扩大到原来的4倍,它的周长就扩大到原来的( 4 )倍,面积就扩大到原来的( 16 )倍。
二.计算下图中阴影部分的面积。
251.2 28.5
三.解决问题。
1.一种独轮车的半径是20厘米,向前转动8圈,前进多少米?
10.048
2.学校花坛的周长是25.12米,它的面积是多少平方米?
50.24
3.从一个长9分米、宽8分米的长方形木板上锯下一个最大的圆,剩下的木板是多少平方分米?
21.76
一个花坛的周长是47.1米。小明在花坛周围滚铁环,铁环直径是30厘米,围着花坛转一周,铁环要转多少圈?
50
课堂小结
(1)圆和圆环面积的公式及应用
(2)圆与四边形(正方形、长方形)的关系
(3)圆的半径、直径、周长、面积之间的关系
圆的半径扩大为原来的几倍,直径、周长也扩大为原来的几倍;面积扩大为原来的平方倍。
课后作业
一、火眼金睛,明辨是非。
1. 在同一个圆里,两条半径就是一条直径。 ( × )
2. 两端都在圆上的线段叫做直径。 ( × )
3. 大圆的圆周率比小圆的圆周率大。 ( × )
4. 如果一个圆的半径增加3厘米,直径就增加6厘米。 ( √ )
5. 圆的周长越长,它的面积越大。 ( √ )
二、反复比较,认真选择。
1. 圆的半径扩大3倍,它的面积扩大( C )倍。
A. 3 B. 6 C. 9
2. 用铁丝围成面积相等的正方形、长方形和圆,( A )用的铁丝最长。
A. 长方形 B. 正方形 C. 圆
3. 半径2米的圆,面积和周长( C )。
A. 相等 B. 不相等 C. 无法比较
4. 把一个圆沿着直径剪成两半,它的面积和周长( A )。
A. 面积不变,周长增加 B. 面积增加,周长不变 C. 面积周长都变
三、求下图形阴影部分的面积。
28.26 50
四、走进生活,解决问题。
1. 一个圆形花坛,直径12米,在它的周围有一条宽2米的环形小路,小路的面积是多少平方米?
87.92
2. 保龄球的半径大约是1dm,球道的长度约为18m,保龄球从球道的一端滚到另一端,最少要滚动多少周?
29
3. 一只闹钟,它的分针长4㎝,这根分针的尖端转动一昼夜所走的路程是多少厘米?
602.88
4.从一个长10分米,宽8分米的长方形木板上锯下一个最大的半圆,剩下的木板是多少平方分米?
54.88
高中★初中★小学专业课外辅导
1 / 9
第11讲:圆的周长与面积
教学目标
1、掌握圆的面积计算公式及应用;
2、掌握圆环面积公式及应用;
3、掌握圆的周长、面积与四边形的关系;
4、圆各部分与圆周长、圆面积的关系。
教学重难点
1、掌握圆的面积与圆环的面积;
2、掌握圆的周长、面积与四边形的关系;
3、圆各部分与圆周长、圆面积的关系。
三、教学过程
课堂回顾
讲评第11讲课后习题
(二)精讲精练
知识点1:圆的面积公式
圆的面积公式的推导:
把一个圆分成若干(偶数)等份,拼成一个近似的长方形,如果分成的分数越多,每一份就会越少,拼成的图形就会越接近长方形。这个长方形的长相当于圆的( 周长的一半 ),宽相当于圆的( 半径 ),公式( )。
例1:请把下面的表格填完整。
半径(r) 直径(d) 圆的周长(c) 圆的面积(s)
0.5m 1m 3.14 0.785
6 12㎝ 37.68 113.04
4 8 25.12dm 50.24
变式训练:求下列图形的周长和面积。
C:18.84 C:22.28
S:28.26 S: 30.28
培优:求两圆阴影部分面积之差。
21.98
知识点2:圆的面积应用
题型一:已知圆的半径,求圆的面积
例1:一个圆形花坛的半径是3m,它的面积是多少?
28.26
题型二:已知圆的直径,求圆的面积。
例2:圆形草坪的直径是20m,每平方米草皮8元。铺满草皮需要多少钱?
2512
题型三:已知圆的周长,求圆的面积
例3:一个圆形蓄水池的周长是25.12m,它的占地面积是多少平方米?
50.24
变式训练:
1. 草地的木桩上拴着一头牛,绳长4米,这头牛能够吃到草的最大面积是多少平方米?
50.24
2.一个运动场(如右图),两端是半圆形,中间是长方形。
沿着这个运动场跑1圈,要跑多少米?
388.4
给这个运动场铺上草坪,一共要铺草坪多少平方米?
8826
3. 把一张长6dm,宽4dm的纸剪成一个最大的圆,剩下部分的面积是多少平方分米?
11.44
知识点3:圆环面积公式
圆环外半径是R,内半径是r,外面大圆的面积是:3.14×R×R,
里面小圆的面积是:3.14×r×r,
圆环面积=大圆面积-小圆面积=3.14×R×R-3.14×r×r=3.14×(R -r )
例1:求出圆环面积。(单位:㎝)
87.92
例2: 在一个直径是16米的圆形喷水池周围铺设一条3米宽的水泥路,这条水泥路的面积是多少平方米?
178.98
变式训练:一块环形铁皮,外圆直径是1.6m,环宽是0.1m.这块铁皮的面积是多少平方厘米?
0.471
培优:
已知阴影部分的面积是5cm ,求圆环的面积。
31.4
知识点4、四边形与圆的关系
在正方形内画最大的圆,圆的直径就等于正方形的边长;在长方形内画一个最大的圆,圆的直径就是长方形的宽;在圆内画出一个最大正方形,圆的直径就等于正方形的对角线。
例1:试在正方形内画出最大的圆,在圆内画出最大的正方形。
2、在一个边长6分米的正方形里剪下一个最大的圆,剩下部分的面积( 7.74 )平方厘米。
变式训练:
1、如右图,圆的周长是( 6.28 )dm,长方形的周长是( 10 )dm。
2、如右图,正方形的周长是4cm,圆的周长是( C )cm。
A.4π B.2π C.π D.π
一张长方形的纸,长是18㎝,宽是12㎝。用这张长方形纸剪一个最大的圆,这个圆的半径多少㎝,周长多少㎝? 6 37.68
4、在一个长20厘米,宽10厘米的长方形纸片里减去一个最大的圆,剩下部分的面积是多少平方厘米。121.5
培优:
1.如下图,已知正方形的面积是20平方厘米,求圆的面积。
62.8
2. 求出下面图中阴影部分的面积。
7.74
知识点5、圆各部分与圆周长、圆面积的关系
圆的半径扩大为原来的几倍,直径、周长也扩大为原来的几倍;面积扩大为原来的平方倍。
例1、判断题:
(1)半径2米的圆,它的周长和面积相等。 ( × )
(2)圆的直径扩大到原来的6倍,它的面积就会扩大到原来的36倍。( √ )
(3)两个圆周长的比一定等于它们面积的比。 ( × )
变式训练:
1、小圆的直径等于大圆的半径,小圆的面积与大圆面积的是( B )。
A. 1∶2 B. 1∶4 C.1∶8
2、如右图,大圆O1和小圆O2面积的比是( B )
A.1:2 B. 1:4
C.2:1 D.4:1
3、如右图,圆面积与正方形面积的比是( C )
π:2 B.2:π C.π:4 D.4:π
培优:
1、如下图所示,两个小圆的周长之和与大圆的周长相比,谁长一些?请说明理由。
一样长
2、一根铁丝分别围成一个长方形、正方形、圆形,( C )的面积最大。
A.长方形 B.正方形 C.圆形 D.不能确定
课堂小测
一.填空
1.把一根6.28米长的铁丝围成一个正方形,则正方形的面积是( 2.4649 )平方米;若围成一个圆,则圆的面积是( 3.14 )平方米。
2.甲圆的半径是乙圆半径的2倍,那么,甲圆的直径是乙圆直径的( 2 )倍,甲圆的周长是乙圆周长的( 2 )倍,甲圆的面积是乙圆面积的( 4 )倍。
3.大圆周长是小圆周长的3倍,大圆面积是小圆面积的( 9 )倍。
4.一个半圆塑料板,半径是1分米,它的周长是( 5.14 )分米。
5.小圆半径是大圆半径的,那么小圆直径是大圆直径的,小圆周长是大圆周长的,小圆面积是大圆面积的。
6.一个圆的半径扩大到原来的4倍,它的周长就扩大到原来的( 4 )倍,面积就扩大到原来的( 16 )倍。
二.计算下图中阴影部分的面积。
251.2 28.5
三.解决问题。
1.一种独轮车的半径是20厘米,向前转动8圈,前进多少米?
10.048
2.学校花坛的周长是25.12米,它的面积是多少平方米?
50.24
3.从一个长9分米、宽8分米的长方形木板上锯下一个最大的圆,剩下的木板是多少平方分米?
21.76
一个花坛的周长是47.1米。小明在花坛周围滚铁环,铁环直径是30厘米,围着花坛转一周,铁环要转多少圈?
50
课堂小结
(1)圆和圆环面积的公式及应用
(2)圆与四边形(正方形、长方形)的关系
(3)圆的半径、直径、周长、面积之间的关系
圆的半径扩大为原来的几倍,直径、周长也扩大为原来的几倍;面积扩大为原来的平方倍。
课后作业
一、火眼金睛,明辨是非。
1. 在同一个圆里,两条半径就是一条直径。 ( × )
2. 两端都在圆上的线段叫做直径。 ( × )
3. 大圆的圆周率比小圆的圆周率大。 ( × )
4. 如果一个圆的半径增加3厘米,直径就增加6厘米。 ( √ )
5. 圆的周长越长,它的面积越大。 ( √ )
二、反复比较,认真选择。
1. 圆的半径扩大3倍,它的面积扩大( C )倍。
A. 3 B. 6 C. 9
2. 用铁丝围成面积相等的正方形、长方形和圆,( A )用的铁丝最长。
A. 长方形 B. 正方形 C. 圆
3. 半径2米的圆,面积和周长( C )。
A. 相等 B. 不相等 C. 无法比较
4. 把一个圆沿着直径剪成两半,它的面积和周长( A )。
A. 面积不变,周长增加 B. 面积增加,周长不变 C. 面积周长都变
三、求下图形阴影部分的面积。
28.26 50
四、走进生活,解决问题。
1. 一个圆形花坛,直径12米,在它的周围有一条宽2米的环形小路,小路的面积是多少平方米?
87.92
2. 保龄球的半径大约是1dm,球道的长度约为18m,保龄球从球道的一端滚到另一端,最少要滚动多少周?
29
3. 一只闹钟,它的分针长4㎝,这根分针的尖端转动一昼夜所走的路程是多少厘米?
602.88
4.从一个长10分米,宽8分米的长方形木板上锯下一个最大的半圆,剩下的木板是多少平方分米?
54.88
高中★初中★小学专业课外辅导
1 / 9
