新人教版八年级下册19.1.1平行四边形性质(1)
文档属性
| 名称 | 新人教版八年级下册19.1.1平行四边形性质(1) |  | |
| 格式 | zip | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-02 19:14:35 | ||
图片预览






文档简介
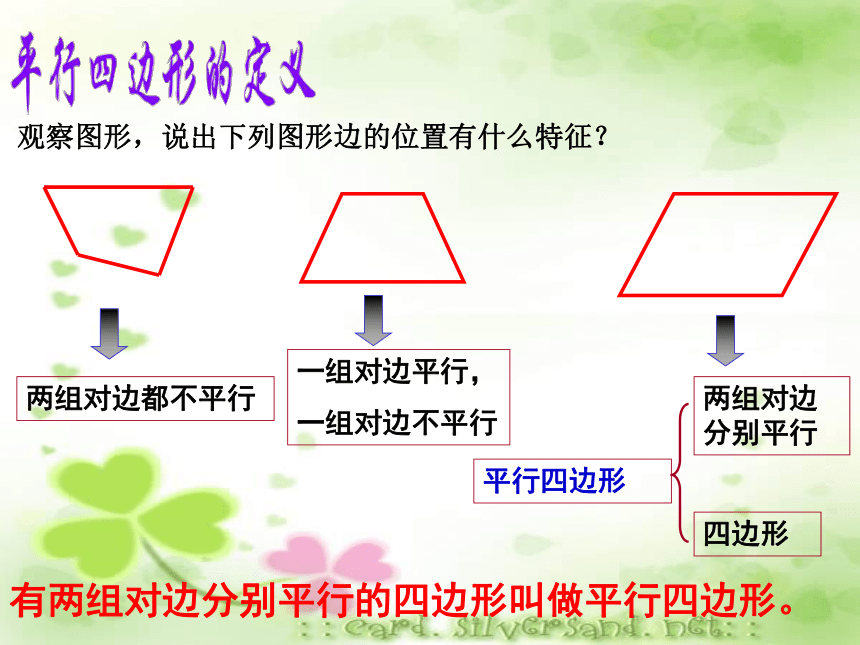
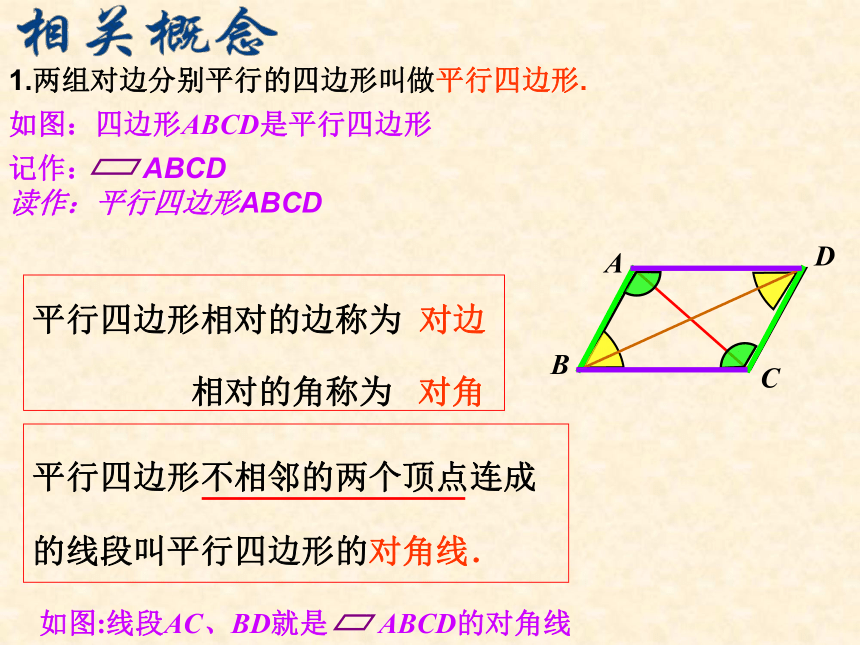
课件71张PPT。平行四边形的性质两组对边都不平行一组对边平行,
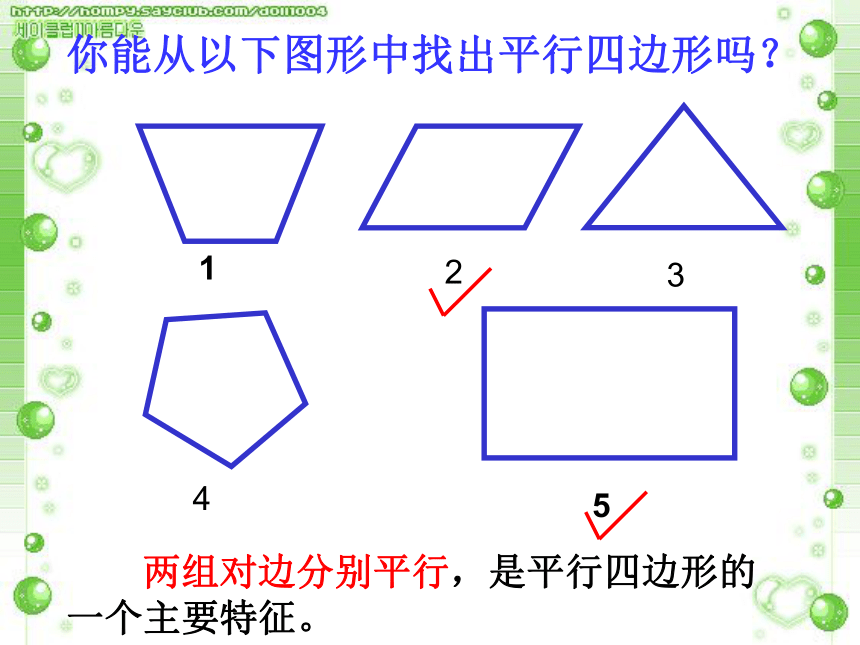
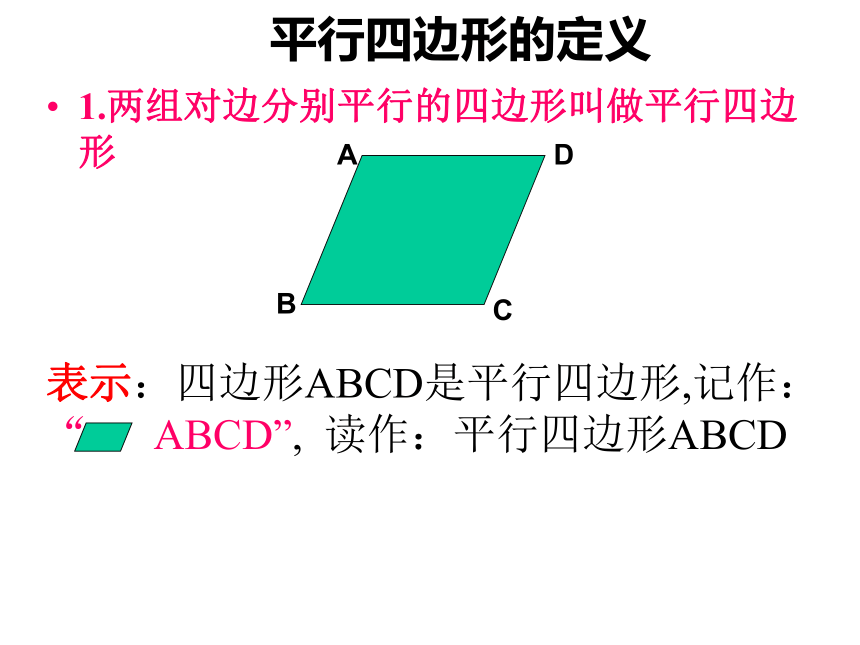
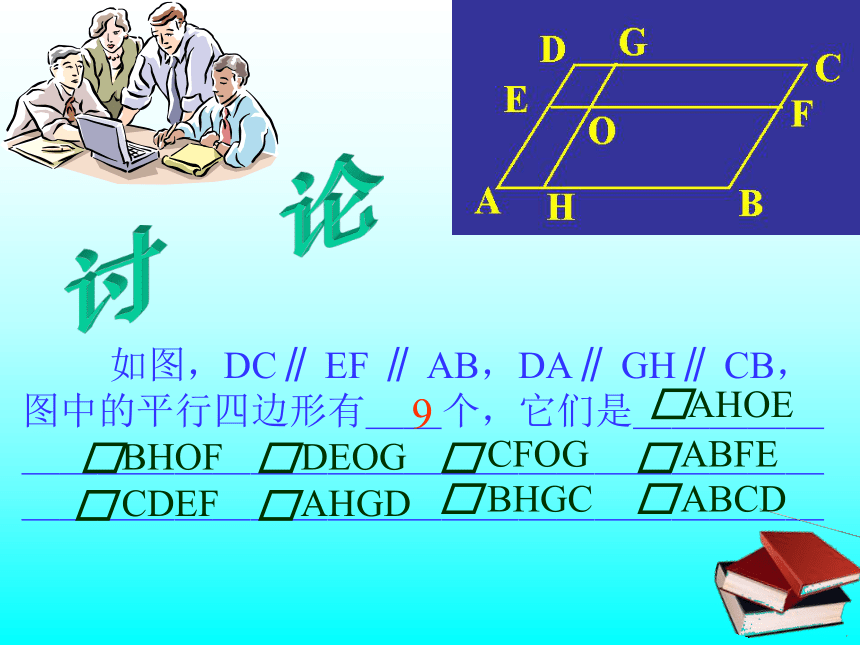
一组对边不平行有两组对边分别平行的四边形叫做平行四边形。观察图形,说出下列图形边的位置有什么特征?你能从以下图形中找出平行四边形吗? 两组对边分别平行,是平行四边形的一个主要特征。231451.两组对边分别平行的四边形叫做平行四边形表示:四边形ABCD是平行四边形,记作: “ ABCD”, 读作:平行四边形ABCDABCD平行四边形的定义 如图,DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有__个,它们是_______________________________________________讨 论91.平行四边形的定义两组对边分别 ????的四边形是平行四边形.答案:平行新 课 早 知2.在四边形ABCD中,AD∥BC,要判定四边形ABCD是平行四边形,那 么还应满足( ????).A.∠A+∠C=180° ????B.∠B+∠D=180°C.∠A+∠B=180° ????D.∠A+∠D=180°答案:D1.四边形的内角和是_____.学 前 温 故2.平行线的性质:(1)两直线平行,同位角____;(2)两直线平行,内错角______;(3)两直线平行,同旁内角____.360°相等相等互补平行四边形相对的边称为 对边
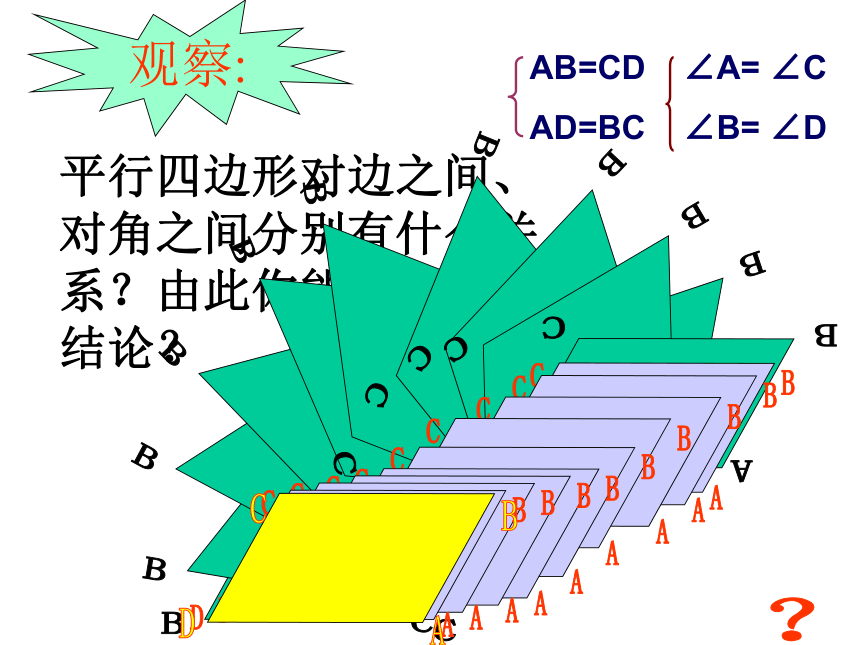
相对的角称为 对角观察:平行四边形对边之间、对角之间分别有什么关系?由此你能得到什么结论? ?ABDC平行四边形对边间的关系用几何语言怎样表示?平行四边形的对边平行.∵四边形ABCD是平行四边形∴AB ∥ CD,BC ∥ AD.∵四边形ABCD是平行四边形∴AB=CD,BC=AD.平行四边形的对边相等.平行四边形的对角相等.∵四边形ABCD是平行四边形
∴∠A= ∠C
∠B= ∠D平行四边形性质平行四边形的两组对边平行且相等观察、测量、实验都不等于证明!你能证明它吗?归纳ACDB已知:如图:四边形ABCD是平行四边形。
求证:AD=BC,AB=CD.
证明:连接AC.∵四边形ABCD是平行四边形, ∴ AD∥BC,AB∥DC. ∴ ∠1=∠2,∠3=∠4.(两直线平行,内错角相等)∴ △ACD≌△CAB. (ASA)
∴AD=CB,AB=CD. (全等三角形的对应边相等)241试一试∵ AC=CA,34.如图,在?ABCD中,∠A=120°,则∠D= ????,∠C= ????.? 答案:60° 120°5.如图,在?ABCD中,AB=5 cm,BC=4 cm,则?ABCD的周长为 ???? ???? cm.? 答案:186.已知?ABCD的面积为4,O为两条对角线的交点,则△AOB的面积 是( ????).A.1 ????B.2 ????C.3 ????D.无法确定答案:A探究 旋转平行四边形,探究平行四边形的对称性平行四边形是中心对称图形.平行四边形的性质几何语言:性质2:平行四边形的两组对边分别平行且相等.(边)∵ 四边形ABCD是平行四边形∴ AB=CD,AD=BC.(平行四边形的对边相等)或∠A= ∠C, ∠B= ∠D(平行四边形的对角相等) ∠A= ∠C, ∠B= ∠D(平行四边形的对角相等) 性质3:平行四边形的两组对角分别相等.(角)性质1:平行四边形是中心对称图形。 思考:平行四边形中相邻的两角有什么关系呢∵四边形ABCD是平行四边形
∴ ∠A+∠B= 180°
∠C+∠D= 180°
1.平行四边形的对边平行且相等. 3.平行四边形的邻角互补: ∠A+∠B= 180°
∠C+∠D= 180°平行四边形的性质 2.平行四边形的对角相等. 4.平行四边形的内角和360°,外角和也为360 °5. 平行四边形是中心对称图形,不是轴对称图形。 如图,四边形ABCD是平行四边形,则:
1)∠ADC= , ∠BCD= ;
2)边AB= ,BC = .58°2832122°叫你的好朋友回答!已知 ABCD中,∠A=80°,你能求出其他各个内角的度数吗?说说你的理由。想一想变式训练一:把条件∠A=80°改成∠A+∠C= 100°,你能求出每个内角的度数吗?变式训练二:把条件∠A=80°改成∠A: ∠B=1:4,你能求出每个内角的度数吗?小组抢答ABCD回可可说:AB=CD=5, BC=AD=8
乐乐:∠A=∠C=40o,∠B= ∠D=130o
聪聪:AB∥CD,BC∥AD
哈哈:∠A+∠C=80o,BC=AD问题2。想一想:谁的测量有误?
(1)可可,乐乐,聪聪,哈哈正在测量
ABCD
回问题3:如图,四边形ABCD和CEFG均为平行四边行。1234ABCD6758FEG可可:∠1+∠8=180o
乐乐:∠4+∠6=180o
聪聪:∠2+ ∠8=180o
哈哈:∠1+ ∠5=180o
谁又错了?回 例题
教学求四边形ABCD的面积回∠BAC=107°请你回答!∠ BAD=133°ABDCE9cm5cm若BE平分∠ABC,则ED=4cm1235cm5cm4cm你可选择答,也可选择别人答!例2.如图 小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少? 解:∵ 四边形ABCD是平行四边形, 且AB=8m
∴AB=CD=8m, AD=BC
又AB+BC+CD+AD=36,
∴ AD=BC=10m知识应用8cm解:∵四边形ABCD是平行四边形(已知)
∴ AB=CD,BC=AD(平行四边形的对边相等)
又∵□ABCD的周长为60cm.
∴AB + BC=30cm.
又AB:BC=3:2,即AB=1.5BC.
则 1.5BC + BC=30 , 解得 BC=12 (cm).
而 AB=1.5×12=18 (cm).变式练习10cm,5cm2运用探究练习2.在 中,周长为24cm,
AD-AB=4cm且 ∠A:∠B=3:1 ,
1)求AB的长度
2)求∠C 的度数。
ABCD变式:若改成求证 FAB= ECD呢?例题探究运用探究26拓展:若点E在CD的延长线上呢?运用探究平行四边形性质的应用【例1】 如图所示,?ABCD的周长为60 cm,对角线相交于点O,△ AOB的周长比△BOC的周长少8 cm,求AB与AD的长.解:设AB=x cm,AD=y cm,根据题意和平行四边形的性质,得?解得? 即AB与AD的长分别为11 cm和19 cm.点拨:数形结合是一种重要的数学思想方法.把几何量之间的关系巧 妙地通过方程组求解,是几何计算中经常用到的方法.【例2】 如图所示,在?ABCD中,BE⊥CD,BF⊥AD,垂足分别是E,F, CE=1,DF=?,∠EBF=60°,则?ABCD的面积为多少?解:∵四边形ABCD是平行四边形,∴AD∥BC.∴∠CBF=∠AFB=90°.∴∠CBE=90°-∠EBF=90°-60°=30°.在Rt△BCE中,BC=2CE=2,BE=?=?,∴AF=?.在Rt△ABF中,∵∠ABF=30°,∴AB=2AF=3.∴S?ABCD=AB·BE=3×?=3?.点拨:在直角三角形中,已知一边和一锐角,可以求出其他的边和角. 在本题中,我们通过解直角三角形,达到求平行四边形面积的目的.【例3】 如图所示,E,F是?ABCD的对角线AC上的点,CE=AF.请你 猜想:BE与DF有怎样的位置关系和数量关系?并对你的猜想加以证 明.分析:根据平行四边形的条件,很容易可以证明△BCE≌△DAF,得出 BE=DF,∠3=∠4,从而可以得出BE∥DF.解:猜想:BE∥DF,BE=DF,证明过程如下:如图所示.∵四边形ABCD是平行四边形.∴BC=AD,BC∥AD.∴∠1=∠2.又∵CE=AF,∴△BCE≌△DAF.∴BE=DF,∠3=∠4.∴BE∥DF点拨:通过观察图形,可猜想线段平行且相等,找线段所在的三角形全 等可以证明所猜想的结论.如果解题时遇到猜想两条线段关系的问 题,无论是否指明,都需要从位置关系和数量关系两方面考虑.情境问题1 一位饱经苍桑的老人,经过一辈子的
辛勤劳动,到晚年的时候,终于拥有
了一块平行四边形的土地,由于年迈
体弱,他决定把这块土地平均分给他的四个孩子,他的三个儿子想出了三种方案,都认为自己是对的,你说他们分得对吗?老二老三老大老大老大分地合理吗?EGFH情境问题2老二分地合理吗?情境问题3老三分地合理吗?老三EF情境问题4 老四想把土地分成相同的四块,
形状如图所示,你能帮他想想办法吗?
?老四我是设计师拼一拼 利用如图的4张小纸片,我们先来动
动手 ,能不能拼成一个平行四边形? 我是设计师想一想老四应该怎么分?学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),现在学校希望这四棵树能组成一个平行四边形,你觉得第四棵树应该栽在哪里?A1A3A2平行四边形的对边平行且相等;平行四边形的对角相等;邻角互补。平行四边形是中心对称图形。有两组对边分别平行的四边形是平行四边形。在 ABCD 中, 已知一个内角的度数是60°,则其余三个内角的度数分别为:大声回答120°、60°、120° 如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?可要细心哟在 ABCD 中, ∠A与∠B 的度数之比为4:5,∠A= , ∠B= , ∠C= ∠D= 。 80°100°80°100° 4.如图,四边形ABCD是平行四边形,若
∠B+∠D= 120°,周长为20,AD:AB=3:2则
1)∠D=_____, ∠BCD=___ ;
2)边CD=____,BC = ____.比一比谁的反应快130°50°33cm15cm100°80°10cm 4、 ABCD的周长为40cm,⊿ABC的周长为25cm,
则对角 线AC长为( )
A、5cm B、15cm C、6cm D、 16cmA 1.如图,在?ABCD中,E是AB延长线上的一点,若∠A=60°,则∠1的度 数为( ????).? A.120° ????B.60° ????C.45° ????D.30°答案:B2.(2011·广州中考)已知?ABCD的周长为32,AB=4,则BC=( ????).A.4 ????B.12 ????C.24 ????D.28解析:由平行四边形的对边分别相等,得BC=?(32-4×2)=12.答案:B3.(2011·湖南邵阳中考)如图所示,在?ABCD中,对角线AC,BD相交 于点O,且AB≠AD,则下列式子不正确的是( ????).? A.AC⊥BD ????B.AB=CDC.BO=OD ? ???D.∠BAD=∠BCD答案:A4.如图,在?ABCD中,∠A=130°,在AD上取DE=DC,则∠ECB的度数 是 ????.? 解析:在?ABCD中,AB∥CD,∠A=130°,∴∠D=180°-∠A=50°.又∵DE=DC,∴∠DCE=65°.∴∠ECB=130°-65°=65°.答案:65°5.若平行四边形的周长是100 cm,且一组邻边的差是30 cm,则较短的 边长是 ????cm;若平行四边形的周长为56 cm,两条邻边的比 是4∶3,则较长边是 ???? cm.答案:10 166.如图所示,在?ABCD中,已知对角线AC和BD相交于点O,△AOB 的周长为15,AB=6,那么对角线AC与BD的和是多少?分析:由平行四边形的对角线互相平分,则AC+BD=2(AO+BO),根据 △AOB的周长和AB的长度可以求出AO与BO的和.解:在?ABCD中,已知AB=6,AO+BO+AB=15,∴AO+BO=15-6=9.又∵AO=OC,BO=OD,∴AC+BD=2AO+2BO=2(AO+BO)=2×9=18.7.如图,在?ABCD中,点E是AD的中点,连接CE并延长,交BA的延长 线于点F.求证:FA=AB.证明:∵四边形ABCD是平行四边形,∴AB=DC,AB∥DC.∴∠FAE=∠D,∠F=∠ECD.又∵EA=ED,∴△AFE≌△DCE.∴AF=DC.∴AF=AB.祝同学们学习进步!课后作业
P98 练习1.2.
一组对边不平行有两组对边分别平行的四边形叫做平行四边形。观察图形,说出下列图形边的位置有什么特征?你能从以下图形中找出平行四边形吗? 两组对边分别平行,是平行四边形的一个主要特征。231451.两组对边分别平行的四边形叫做平行四边形表示:四边形ABCD是平行四边形,记作: “ ABCD”, 读作:平行四边形ABCDABCD平行四边形的定义 如图,DC∥ EF ∥ AB,DA∥ GH∥ CB,图中的平行四边形有__个,它们是_______________________________________________讨 论91.平行四边形的定义两组对边分别 ????的四边形是平行四边形.答案:平行新 课 早 知2.在四边形ABCD中,AD∥BC,要判定四边形ABCD是平行四边形,那 么还应满足( ????).A.∠A+∠C=180° ????B.∠B+∠D=180°C.∠A+∠B=180° ????D.∠A+∠D=180°答案:D1.四边形的内角和是_____.学 前 温 故2.平行线的性质:(1)两直线平行,同位角____;(2)两直线平行,内错角______;(3)两直线平行,同旁内角____.360°相等相等互补平行四边形相对的边称为 对边
相对的角称为 对角观察:平行四边形对边之间、对角之间分别有什么关系?由此你能得到什么结论? ?ABDC平行四边形对边间的关系用几何语言怎样表示?平行四边形的对边平行.∵四边形ABCD是平行四边形∴AB ∥ CD,BC ∥ AD.∵四边形ABCD是平行四边形∴AB=CD,BC=AD.平行四边形的对边相等.平行四边形的对角相等.∵四边形ABCD是平行四边形
∴∠A= ∠C
∠B= ∠D平行四边形性质平行四边形的两组对边平行且相等观察、测量、实验都不等于证明!你能证明它吗?归纳ACDB已知:如图:四边形ABCD是平行四边形。
求证:AD=BC,AB=CD.
证明:连接AC.∵四边形ABCD是平行四边形, ∴ AD∥BC,AB∥DC. ∴ ∠1=∠2,∠3=∠4.(两直线平行,内错角相等)∴ △ACD≌△CAB. (ASA)
∴AD=CB,AB=CD. (全等三角形的对应边相等)241试一试∵ AC=CA,34.如图,在?ABCD中,∠A=120°,则∠D= ????,∠C= ????.? 答案:60° 120°5.如图,在?ABCD中,AB=5 cm,BC=4 cm,则?ABCD的周长为 ???? ???? cm.? 答案:186.已知?ABCD的面积为4,O为两条对角线的交点,则△AOB的面积 是( ????).A.1 ????B.2 ????C.3 ????D.无法确定答案:A探究 旋转平行四边形,探究平行四边形的对称性平行四边形是中心对称图形.平行四边形的性质几何语言:性质2:平行四边形的两组对边分别平行且相等.(边)∵ 四边形ABCD是平行四边形∴ AB=CD,AD=BC.(平行四边形的对边相等)或∠A= ∠C, ∠B= ∠D(平行四边形的对角相等) ∠A= ∠C, ∠B= ∠D(平行四边形的对角相等) 性质3:平行四边形的两组对角分别相等.(角)性质1:平行四边形是中心对称图形。 思考:平行四边形中相邻的两角有什么关系呢∵四边形ABCD是平行四边形
∴ ∠A+∠B= 180°
∠C+∠D= 180°
1.平行四边形的对边平行且相等. 3.平行四边形的邻角互补: ∠A+∠B= 180°
∠C+∠D= 180°平行四边形的性质 2.平行四边形的对角相等. 4.平行四边形的内角和360°,外角和也为360 °5. 平行四边形是中心对称图形,不是轴对称图形。 如图,四边形ABCD是平行四边形,则:
1)∠ADC= , ∠BCD= ;
2)边AB= ,BC = .58°2832122°叫你的好朋友回答!已知 ABCD中,∠A=80°,你能求出其他各个内角的度数吗?说说你的理由。想一想变式训练一:把条件∠A=80°改成∠A+∠C= 100°,你能求出每个内角的度数吗?变式训练二:把条件∠A=80°改成∠A: ∠B=1:4,你能求出每个内角的度数吗?小组抢答ABCD回可可说:AB=CD=5, BC=AD=8
乐乐:∠A=∠C=40o,∠B= ∠D=130o
聪聪:AB∥CD,BC∥AD
哈哈:∠A+∠C=80o,BC=AD问题2。想一想:谁的测量有误?
(1)可可,乐乐,聪聪,哈哈正在测量
ABCD
回问题3:如图,四边形ABCD和CEFG均为平行四边行。1234ABCD6758FEG可可:∠1+∠8=180o
乐乐:∠4+∠6=180o
聪聪:∠2+ ∠8=180o
哈哈:∠1+ ∠5=180o
谁又错了?回 例题
教学求四边形ABCD的面积回∠BAC=107°请你回答!∠ BAD=133°ABDCE9cm5cm若BE平分∠ABC,则ED=4cm1235cm5cm4cm你可选择答,也可选择别人答!例2.如图 小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少? 解:∵ 四边形ABCD是平行四边形, 且AB=8m
∴AB=CD=8m, AD=BC
又AB+BC+CD+AD=36,
∴ AD=BC=10m知识应用8cm解:∵四边形ABCD是平行四边形(已知)
∴ AB=CD,BC=AD(平行四边形的对边相等)
又∵□ABCD的周长为60cm.
∴AB + BC=30cm.
又AB:BC=3:2,即AB=1.5BC.
则 1.5BC + BC=30 , 解得 BC=12 (cm).
而 AB=1.5×12=18 (cm).变式练习10cm,5cm2运用探究练习2.在 中,周长为24cm,
AD-AB=4cm且 ∠A:∠B=3:1 ,
1)求AB的长度
2)求∠C 的度数。
ABCD变式:若改成求证 FAB= ECD呢?例题探究运用探究26拓展:若点E在CD的延长线上呢?运用探究平行四边形性质的应用【例1】 如图所示,?ABCD的周长为60 cm,对角线相交于点O,△ AOB的周长比△BOC的周长少8 cm,求AB与AD的长.解:设AB=x cm,AD=y cm,根据题意和平行四边形的性质,得?解得? 即AB与AD的长分别为11 cm和19 cm.点拨:数形结合是一种重要的数学思想方法.把几何量之间的关系巧 妙地通过方程组求解,是几何计算中经常用到的方法.【例2】 如图所示,在?ABCD中,BE⊥CD,BF⊥AD,垂足分别是E,F, CE=1,DF=?,∠EBF=60°,则?ABCD的面积为多少?解:∵四边形ABCD是平行四边形,∴AD∥BC.∴∠CBF=∠AFB=90°.∴∠CBE=90°-∠EBF=90°-60°=30°.在Rt△BCE中,BC=2CE=2,BE=?=?,∴AF=?.在Rt△ABF中,∵∠ABF=30°,∴AB=2AF=3.∴S?ABCD=AB·BE=3×?=3?.点拨:在直角三角形中,已知一边和一锐角,可以求出其他的边和角. 在本题中,我们通过解直角三角形,达到求平行四边形面积的目的.【例3】 如图所示,E,F是?ABCD的对角线AC上的点,CE=AF.请你 猜想:BE与DF有怎样的位置关系和数量关系?并对你的猜想加以证 明.分析:根据平行四边形的条件,很容易可以证明△BCE≌△DAF,得出 BE=DF,∠3=∠4,从而可以得出BE∥DF.解:猜想:BE∥DF,BE=DF,证明过程如下:如图所示.∵四边形ABCD是平行四边形.∴BC=AD,BC∥AD.∴∠1=∠2.又∵CE=AF,∴△BCE≌△DAF.∴BE=DF,∠3=∠4.∴BE∥DF点拨:通过观察图形,可猜想线段平行且相等,找线段所在的三角形全 等可以证明所猜想的结论.如果解题时遇到猜想两条线段关系的问 题,无论是否指明,都需要从位置关系和数量关系两方面考虑.情境问题1 一位饱经苍桑的老人,经过一辈子的
辛勤劳动,到晚年的时候,终于拥有
了一块平行四边形的土地,由于年迈
体弱,他决定把这块土地平均分给他的四个孩子,他的三个儿子想出了三种方案,都认为自己是对的,你说他们分得对吗?老二老三老大老大老大分地合理吗?EGFH情境问题2老二分地合理吗?情境问题3老三分地合理吗?老三EF情境问题4 老四想把土地分成相同的四块,
形状如图所示,你能帮他想想办法吗?
?老四我是设计师拼一拼 利用如图的4张小纸片,我们先来动
动手 ,能不能拼成一个平行四边形? 我是设计师想一想老四应该怎么分?学校买了四棵树,准备栽在花园里,已经栽了三棵(如图),现在学校希望这四棵树能组成一个平行四边形,你觉得第四棵树应该栽在哪里?A1A3A2平行四边形的对边平行且相等;平行四边形的对角相等;邻角互补。平行四边形是中心对称图形。有两组对边分别平行的四边形是平行四边形。在 ABCD 中, 已知一个内角的度数是60°,则其余三个内角的度数分别为:大声回答120°、60°、120° 如图,小明用一根36m长的绳子围成了一个平行四边形的场地,其中一条边AB长为8m,其他三条边各长多少?可要细心哟在 ABCD 中, ∠A与∠B 的度数之比为4:5,∠A= , ∠B= , ∠C= ∠D= 。 80°100°80°100° 4.如图,四边形ABCD是平行四边形,若
∠B+∠D= 120°,周长为20,AD:AB=3:2则
1)∠D=_____, ∠BCD=___ ;
2)边CD=____,BC = ____.比一比谁的反应快130°50°33cm15cm100°80°10cm 4、 ABCD的周长为40cm,⊿ABC的周长为25cm,
则对角 线AC长为( )
A、5cm B、15cm C、6cm D、 16cmA 1.如图,在?ABCD中,E是AB延长线上的一点,若∠A=60°,则∠1的度 数为( ????).? A.120° ????B.60° ????C.45° ????D.30°答案:B2.(2011·广州中考)已知?ABCD的周长为32,AB=4,则BC=( ????).A.4 ????B.12 ????C.24 ????D.28解析:由平行四边形的对边分别相等,得BC=?(32-4×2)=12.答案:B3.(2011·湖南邵阳中考)如图所示,在?ABCD中,对角线AC,BD相交 于点O,且AB≠AD,则下列式子不正确的是( ????).? A.AC⊥BD ????B.AB=CDC.BO=OD ? ???D.∠BAD=∠BCD答案:A4.如图,在?ABCD中,∠A=130°,在AD上取DE=DC,则∠ECB的度数 是 ????.? 解析:在?ABCD中,AB∥CD,∠A=130°,∴∠D=180°-∠A=50°.又∵DE=DC,∴∠DCE=65°.∴∠ECB=130°-65°=65°.答案:65°5.若平行四边形的周长是100 cm,且一组邻边的差是30 cm,则较短的 边长是 ????cm;若平行四边形的周长为56 cm,两条邻边的比 是4∶3,则较长边是 ???? cm.答案:10 166.如图所示,在?ABCD中,已知对角线AC和BD相交于点O,△AOB 的周长为15,AB=6,那么对角线AC与BD的和是多少?分析:由平行四边形的对角线互相平分,则AC+BD=2(AO+BO),根据 △AOB的周长和AB的长度可以求出AO与BO的和.解:在?ABCD中,已知AB=6,AO+BO+AB=15,∴AO+BO=15-6=9.又∵AO=OC,BO=OD,∴AC+BD=2AO+2BO=2(AO+BO)=2×9=18.7.如图,在?ABCD中,点E是AD的中点,连接CE并延长,交BA的延长 线于点F.求证:FA=AB.证明:∵四边形ABCD是平行四边形,∴AB=DC,AB∥DC.∴∠FAE=∠D,∠F=∠ECD.又∵EA=ED,∴△AFE≌△DCE.∴AF=DC.∴AF=AB.祝同学们学习进步!课后作业
P98 练习1.2.
