新人教版八年级下册19.1.2平行四边形的判定(1)
文档属性
| 名称 | 新人教版八年级下册19.1.2平行四边形的判定(1) |  | |
| 格式 | zip | ||
| 文件大小 | 992.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-02 19:15:02 | ||
图片预览



文档简介
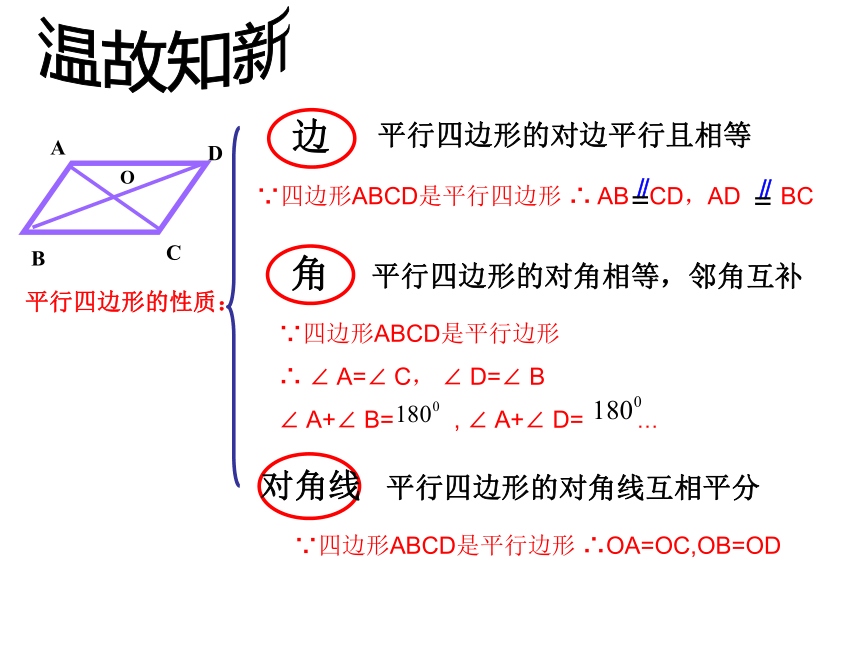
课件69张PPT。平行四边形的判定 (1)平行四边形的对边平行且相等 平行四边形的对角线互相平分 温故知新平行四边形的性质:O平行四边形的对角相等,邻角互补
∵四边形ABCD是平行边形
∴ ∠ A=∠ C, ∠ D=∠ B
∠ A+∠ B= , ∠ A+∠ D= …
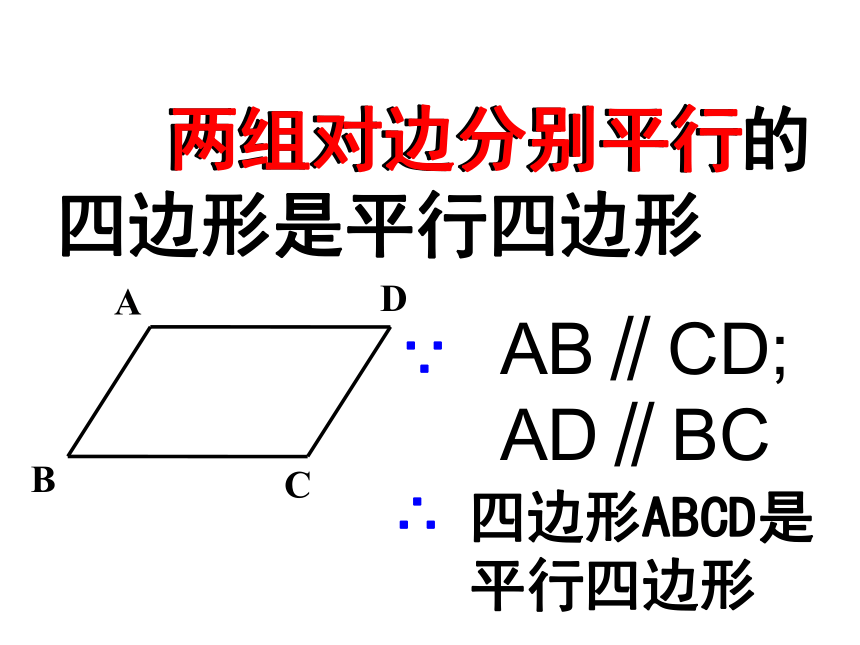
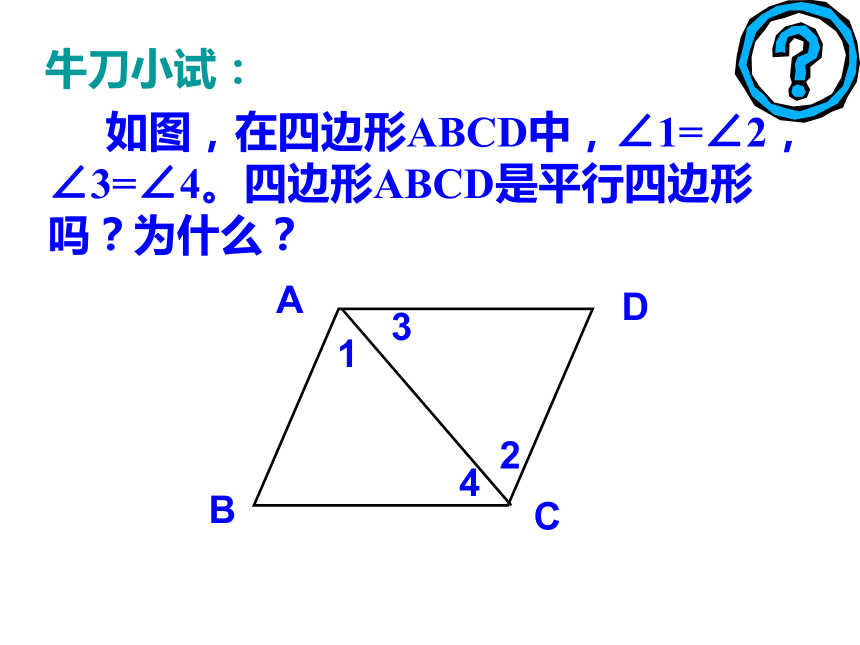
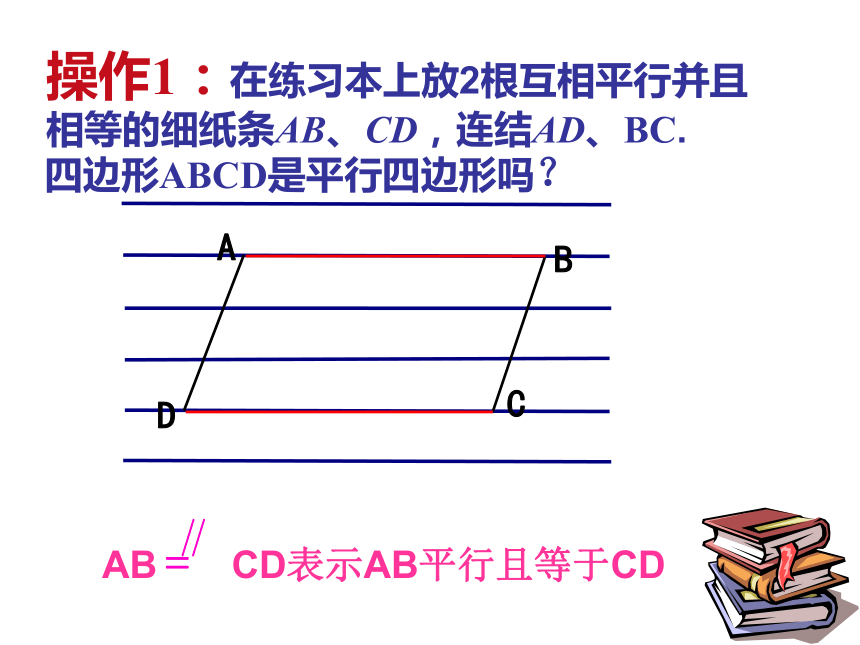
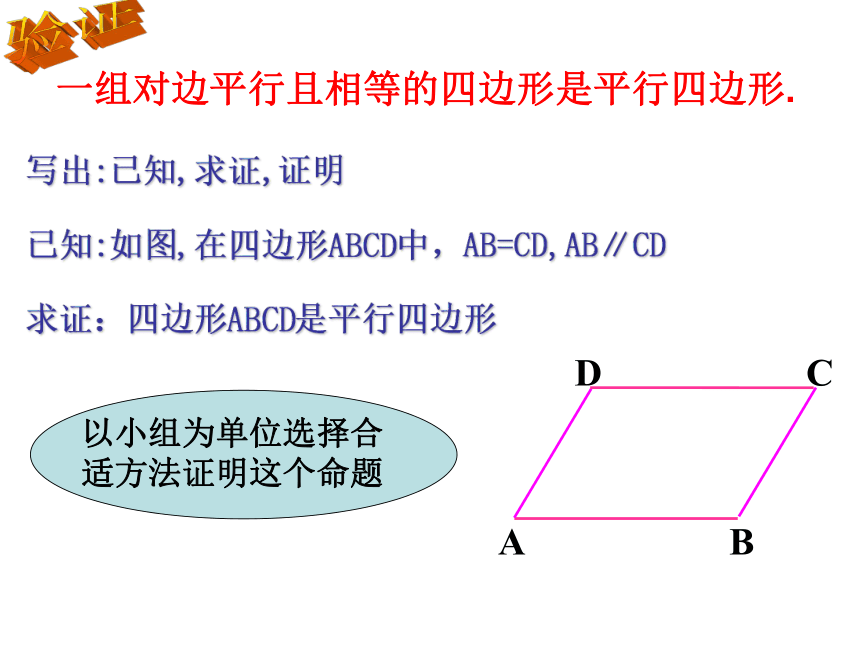
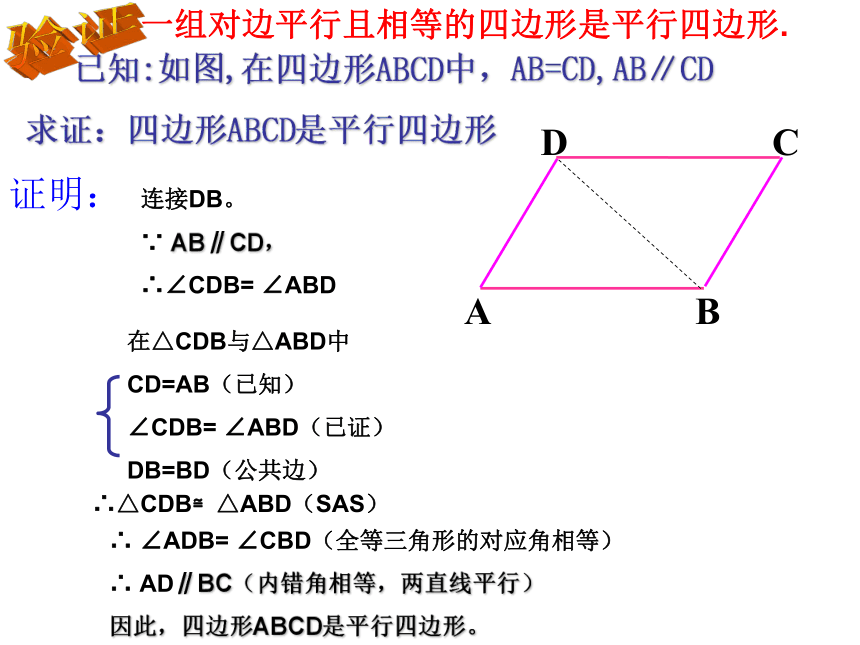
∵四边形ABCD是平行边形 ∴OA=OC,OB=OD 温故知新什么样的四边形是平行四边形?我们学过的 两组对边分别平行的 四边形是平行四边形两组对边分别平行∵∴四边形ABCD是平行四边形AB∥CD; AD∥BC 如图,在四边形ABCD中,∠1=∠2,∠3=∠4。四边形ABCD是平行四边形吗?为什么?牛刀小试:操作1:在练习本上放2根互相平行并且相等的细纸条AB、CD,连结AD、BC.四边形ABCD是平行四边形吗?ADBCAB CD表示AB平行且等于CD一组对边平行且相等的四边形是平行四边形. 写出:已知,求证,证明已知:如图,在四边形ABCD中,AB=CD,AB∥CD求证:四边形ABCD是平行四边形验证已知:如图,在四边形ABCD中,AB=CD,AB∥CD求证:四边形ABCD是平行四边形验证证明:连接DB。
∵ AB∥CD,
∴∠CDB= ∠ABD在△CDB与△ABD中
CD=AB(已知)
∠CDB= ∠ABD(已证)
DB=BD(公共边) ∴△CDB≌△ABD(SAS)∴ ∠ADB= ∠CBD(全等三角形的对应角相等)
∴ AD∥BC(内错角相等,两直线平行)
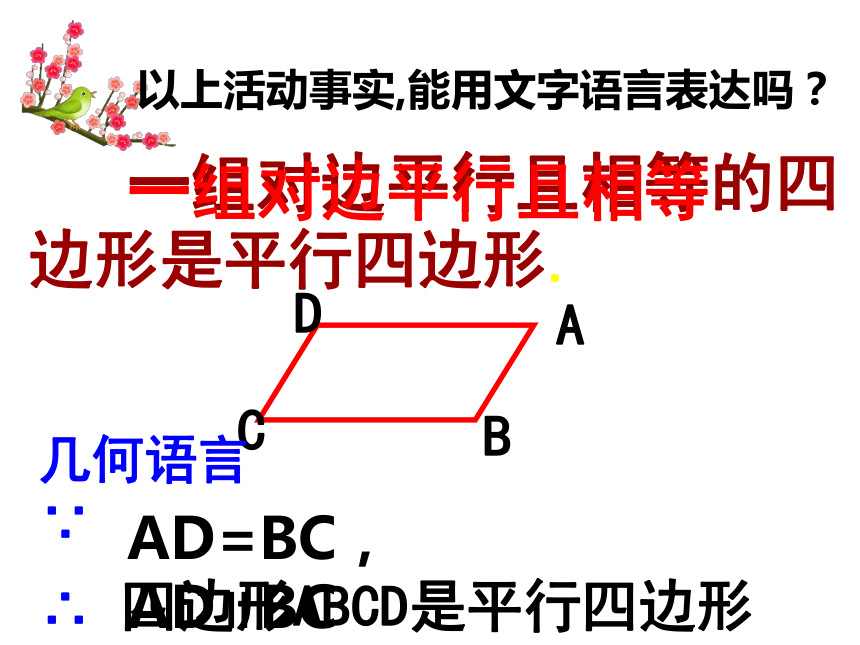
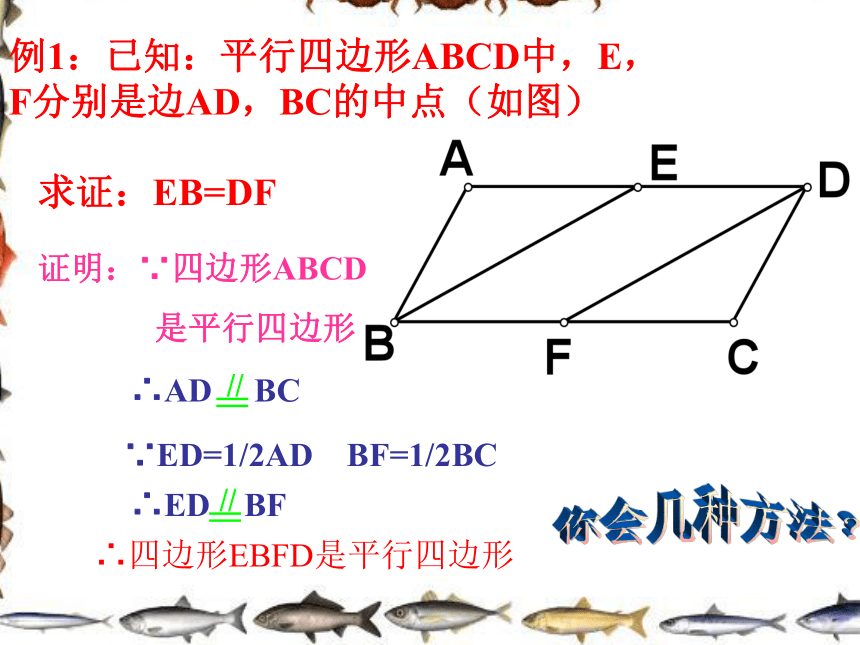
因此,四边形ABCD是平行四边形。一组对边平行且相等的四边形是平行四边形. 几何语言∵∴AD=BC, AD∥BC四边形ABCD是平行四边形 一组对边平行且相等的四边形是平行四边形.一组对边平行且相等 以上活动事实,能用文字语言表达吗? 例1:已知:平行四边形ABCD中,E,F分别是边AD,BC的中点(如图) 求证:EB=DF 证明:∵四边形ABCD
是平行四边形 ∴AD BC ∵ED=1/2AD BF=1/2BC ∴ED BF ∴四边形EBFD是平行四边形
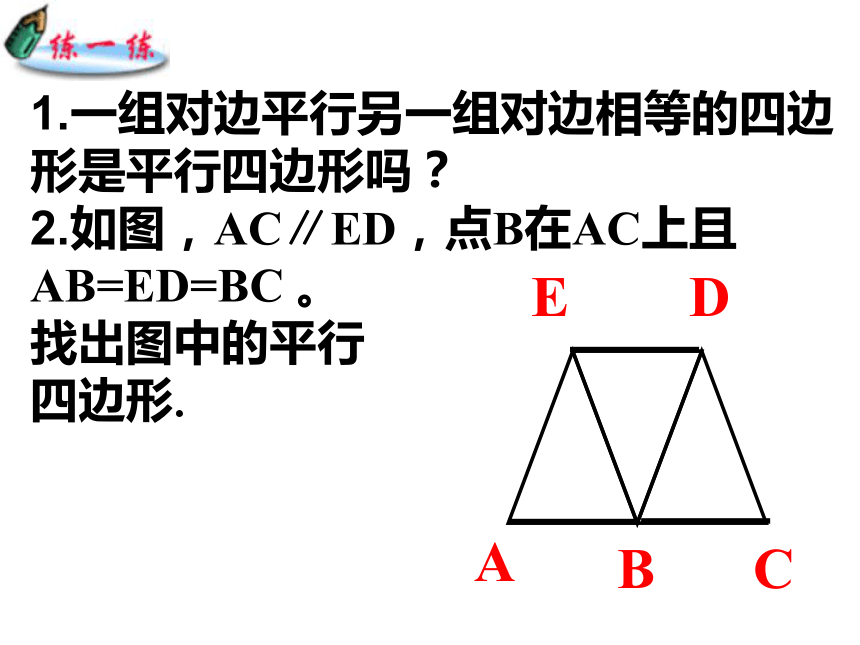
你会几种方法?1.一组对边平行另一组对边相等的四边形是平行四边形吗?
2.如图,AC∥ED,点B在AC上且AB=ED=BC 。
找出图中的平行
四边形.
操作2工具:两对长度分别相等的细纸条. 动手:能否在平面内用这四根细纸条摆成一个平行四边形?试试看!思考:你能说明你们摆出的四边形
是平行四边形吗?平行四边形的对边相等。
逆命题:两组对边分别相等的四边形是平行四边形。已知:四边形ABCD, AB=CD,AD=BC
求证:四边形ABCD是平行四边形证明:
∵ 在△ABC与△CDA中
AB=CD(已知)
AD=BC (已知)
AC=CA (公共边)
∴△ABC≌△CDA(SSS)∴∠1=∠2,∠3=∠4(全等三角形的对应边相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
∴四边形ABCD是平行四边形BDAC2134验证连结AC,几何语言∵∴AD=BC,DC=AB四边形ABCD是平行四边形以上活动事实,能用文字语言表达吗? 两组对边分别相等的四边形是平行四边形.两组对边分别相等 工人师傅做铝合金窗框分下面三个步骤进行:
(1) 先截出两对符合规格的铝合金窗料(如图①)使AB=CD,EF=GH;
(2)摆放成如图②的四边形,则这时铝合金窗框的形状是 ,
根据的数学道理是: ;
平行四边形两组对边分别相等的四边行是平行四边形驶向胜利的彼岸 如图将两长两短的四根细木条用小钉绞合在一起,做成一个四边形,使等长的木条成为对边.转动这个四边形,使它形状改变,在图形变化的过程中,它一直是一个平行四边形吗?1. 对于四边形ABCD,如果从条件①AB∥CD
②AD∥BC③AB=CD④BC=AD中选出2个,
那么能 说明四边形ABCD是平行四边形的有
_______(填序号,填出符合条件的一种情
况即可)
对角相等的四边形是平行四边形。平行四边形的对角相等的逆命题是:已知四边形ABCD中∠A=∠ C,∠B=∠D,
求证:四边形ABCD是平行四边形。证明:∵∠A+∠B+∠C+∠D=360°且∠C=∠A ,∠D=∠B∴∠A+∠B+∠A+∠B=360°即:2∠A+2∠B=360°2(∠A+∠B)=360°∠A+∠B=180°∴AD∥BC同理:AB∥CD ∴四边形ABCD是平行
四边形对角线互相平分的四边形是平行四边形。平行四边形的对角线互相平分的逆命题是:已知四边形ABCD的对角线AC,BD相交于点O,并且 AO=CO,BO=DO,
求证:四边形ABCD是平行四边形。证明:在△AOB和△COD中∴ △AOB ≌ △COD (SAS)∴AB=CD同理 : AD=CB∴四边形ABCD是平行四边形(两组对边分别相等的四 边形是平行四边形。) 如图,将两根细木条AC、BD的中心重叠,用小钉绞合在一起,用橡皮筋连接木条的顶点,做成一个四边形ABCD,转动两根木条,它一直是一个平行四边形吗?你能证明吗?你又能得到什么结论? 对角线互相平分的四边形是平行四边形你也试一试从边来判定1、两组对边分别平行的四边形是平行四边形(定义) 2、两组对边分别相等的四边形是平行四边形3、一组对边平行且相等的四边形是平行四边形从角来判定两组对角分别相等的四边形是平行四边形从对角线来判定两条对角线互相平分的四边形是平行四边形四、理一理平行四边形的判定方法1、请你识别下列四边形哪些是平行四边形?为什么?⑴⑷
⑶ABCD120°60°5㎝5㎝BADC4.8㎝4.8㎝⑵7.6㎝7.6㎝五、试一试 2、在下列条件中,不能判定四边形是平行四边形的是( )
AB∥CD,AD∥BC
AB=CD,AD=BC
(C)AB∥CD,AB=CD
(D) AB∥CD,AD=BC
(E) AB∥CD, ∠A=∠CD(两组对边分别平行)(两组对边分别相等)(一组对边平行且相等)(两组对角分别相等)开心一练:1.根据下列条件,不能判定一个四边形为平行四边形的是( )
(A)两组对边分别相等
(B)两条对角线互相平分
(C)两条对角线相等
(D)两组对边分别平行C挑战第一关:驶向胜利的彼岸已知:如图求证:四边形MNOP是
平行四边形.数学联想:1、小强给我们了一些什么条件?2、由MO⊥ON联想到什么?边长(含X)、MO⊥ON勾股定理、求x同学们真棒!
这是一道综合运用勾股定理、方程、平行四边形的题目,由这道题我们可以看出,有些几何问题能用代数知识解决。 1、下列条件中,不能判定四边形ABCD是平行四边形的是( )
A、∠A=∠C,∠B=∠D
∠A=∠B=∠C=90
∠A+∠B=180 ,∠B+∠C=180
∠A+∠B=180 ,∠C+∠D=180D2、如图,在平行四边形ABCD的一组对边AD、BC上截取EF=MN,连接EM、FN,EM和FN有怎样的关系?为什么?巩固练习BDACMNEF例1 如图,AB =DC=EF, AD=BC,DE=CF,则图中有哪些互相平行的线段?看谁最快AB ∥ DC∥ EFAD ∥ BCDE ∥ CF例2 已知: 中,M、N、P、Q分别是AB、BC、CD、DA的中点
求证:四边形MNPQ是平行四边形好题大家练例3 如图:四边形ABCD是梯形,在底边AB上求作一点E,使四边形AECD为平行四边形。大显身手大显身手证明一: 四边形ABCD是平行四边形AD ∥ BC且AD =BCEAD= FCBAE=CF
EAD= FCB
AD=BCAED ≌ CFB(SAS)DE=BF四边形BFDE是平行四边形在 AED和 CFB中同理可证:BE=DF4、已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形大显身手4、已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形DOABCEF证明二:作对角线BD,交AC于点O。
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形
大显身手变式1:已知:E、F是平行四边形ABCD对角线AC上的两点,并且
求证:四边形BFDE是平行四边形DABCEFBE∥DF大显身手变式2:已知:E、F是平行四边形ABCD对角线AC上的两点,并且
求证:四边形BFDE是平行四边形DABCEFBE⊥AC于E,DF⊥AC于F大显身手变式3:已知:E、F是平行四边形ABCD对角线AC上的两点,并且
求证:四边形BFDE是平行四边形DABCEFBE=DF动动脑ABCDMNPQO已知:在平行四边形ABCD中,对角线AC 、BD相交于点,M 、 N 、 P、 Q分别是OA 、OB 、OC 、 OD
的中点
求证 四边形MNPQ是平行四边形15 例2(2009年新疆)如图,是四边形的对角线上两点,AF=CE,DF=BE,DF∥BE 求证:(1) (2)四边形ABCD是平行四边形. 证明:(1) ,
问题2:若将这三个点放入到平面直角坐标系中,其中A点坐标为(4,5),B点坐标为(2,0),C点坐标为(7,0),你能求出以A、B、C、D四点为顶点构成平行四边形的第四个顶点点D的坐标吗?活动四:应用定理 昨天初一的李明同学在生物实验室做实验时,不小心碰碎了实验室的一块平行四边形的实验用的玻璃片,只剩下如图所示部分,他想明天星期六回家去割一块赔给学校,带上玻璃剩下部分去玻璃店不安全,于是他想把原来的平行四边形重新在纸上画出来?然后带上图纸去就行了,可原来的平行四边形怎么给它画出来呢?(A,B,C为三顶点,即找出第四个顶点D)生活实际的挑战方法(一)DAB∥CD,AD∥BC∴四边形ABCD是平行四边形方法(二)D两组对边分别相等的四边形是平行四边形方法(三)D方法(四)D两组对角分别相等的四边形是平行四边形方法(五)DO对角线互相平分的四边形是平行四边形已知:如图,在平行四边形ABCD的周长为20cm,O是对角线AC和BD的交点
(1)若△ABC的周长是7cm,求OC的长
(2)若△OAB的周长比△OBC的周长短4cm,求AB的长O4.如图 四边形 ABCD和四边形BEDF都是平行四边形, 请你说明(1) AE=CF的理由
O变式:如图 已知 四边形 ABCD都是平行四边形, AE=CF,请你说明四边形BEDF是平行四边形
拓展训练1 2、已知:AD为△ABC的角平分线,DE∥AB ,在AB上截取BF=AE。
求证:EF=BD
123
3、已知 平行四边形 ABCD中,直线MN // AC,分别交DA延长线于M,DC延长线于N,AB于P,BC于Q。
求证:PM=QN。例2:如图,在△ABC中,AB=14,BC=18,AD是AC边上的中线,求BD的取值范围。两组对边分别相等两组对角分别相等对角线互相平分两组对边分别平行平行四边形的判定方法一组对边平行且相等四边形是平行四边形边角对角线:谈谈你有何收获吧!六、说一说:
1.本节课你学会了几种平行四边形的判定方法2.本节课所学的解决问题的思路是: (2)碰到平行四边形的问题常转化为三角形来解决.(1)解决一个数学问题,常要通过”动手实践”-----”
猜想”-----”验证猜想(证明)”-----”得出结论”2.能够判定四边形ABCD是平行四边形的条件是( ????).A.AB∥CD,AD=BCB.∠A=∠B,∠C=∠DC.AB=CD,AD=BCD.AB=AD,CB=CD答案:C3.如右图所示,四边形ABCD的对角线AC和BD相交于点O,下列判断 正确的是( ????).A.若AO=OC,则四边形ABCD是平行四边形B.若AC=BD,则四边形ABCD是平行四边形C.若AO=BO,CO=DO,则四边形ABCD是平行四边形D.若AO=OC,BO=OD,则四边形ABCD是平行四边形答案:D4.连接三角形两边 ????的线段叫做三角形的中位线.答案:中点5.三角形中位线定理三角形的中位线 ????于三角形的第三边,且等于第三边的 ????.答案:平行 一半6.已知在△ABC中,BC=6 cm,E,F分别是AB,AC的中点,那么EF的长是 ???? cm.答案:37.两条平行线间的任何两条平行线段都 ????.答案:相等1.平行四边形的性质与判定的综合应用【例1】 已知,如图所示,AD为△ABC的中线,E为AC上一点,连接BE 交AD于F,且AE=FE.求证:BF=AC.? 分析:延长AD到N,使DN=AD,构造出平行四边形ABNC求解即可.证明:延长AD到N,使DN=AD,连接BN,CN,∵BD=CD,AD=ND,∴四边形ABNC是平行四边形.∴BN=AC,BN∥AC.∴∠FAE=∠BND.∵AE=FE,∴∠FAE=∠AFE.∵∠AFE=∠BFD,∠FAE=∠BND,∴∠BFD=∠BND,∴BN=BF.∴BF=AC.点拨:有三角形中线时,常延长中线构造平行四边形,然后再利用平行 四边形的性质转化线段或角的相等进行证题.2.三角形中位线定理的运用【例2】 如图所示,已知E,F,G,H分别是线段AB,BD,CD,CA的中点, 求证:四边形EFGH是平行四边形.分析:本题出现多个中点,应想到三角形中位线.E,H分别为AB,AC的中点,那么连接BC后,EH为△ABC的中位线,可 利用中位线证明.证明:连接BC,AD,∵H为AC的中点,E为AB的中点,∴EH∥BC,EH=?BC.又∵G为CD的中点,F为BD的中点,∴GF∥BC,GF=?BC.∴EH∥GF且EH=GF.∴四边形EFGH为平行四边形.点拨:当题目中已知线段的中点时,一般应考虑运用三角形的中位线 定理,取中点构造中位线是作辅助线的常用方法.1.下列条件不能判断四边形ABCD是平行四边形的是( ????).A.∠A=∠C,∠B=∠D ????B.AD=BC,AB=CDC.AB=CD,AD∥BC ????D.AB∥CD,AD∥BC解析:一组对边平行且相等的四边形是平行四边形,故C错误.答案:C2.小明的爸爸在钉制平行四边形框架时,采用了一种方法:将两根木 条AC,BD的中点重叠,并用钉子固定,则四边形ABCD就是平行四边 形,这种方法的依据是( ????).A.两组对边分别平行的四边形是平行四边形B.对角线互相平分的四边形是平行四边形C.一组对边平行且相等的四边形是平行四边形D.两组对角分别相等的四边形是平行四边形答案:B3.(2011·山东德州中考)如图,D,E,F分别为△ABC三边的中点,则图中 平行四边形的个数为 ????.解析:由三角形的中位线定理得,DE∥AC,DF∥BC,EF∥AB.所以由 平行四边形的定义得,四边形ADEF、四边形BEFD、四边形ECFD 是平行四边形.答案:34.在四边形ABCD中,AB∥CD,要使四边形ABCD为平行四边形,则可 添加的条件为 ????.(填一个即可)答案:答案不唯一,如AB=CD或∠A=∠C或AD∥BC5.在?ABCD中,分别以AD,BC为边向内作等边△ADE和等边△ BCF,连接BE,DF.求证:四边形BEDF是平行四边形.证明:∵四边形ABCD是平行四边形,∴CD=AB,AD=CB,∠DAB=∠BCD.又∵△ADE和△CBF都是等边三角形,∴DE=BF,AE=CF,∠DAE=∠BCF=60°.∵∠DCF=∠BCD-∠BCF,∠BAE=∠DAB-∠DAE,∴∠DCF=∠ BAE.∴△DCF≌△BAE(SAS).∴DF=BE.∴四边形BEDF是平行四边形.6.如图,在?ABCD中,点E是AD的中点,BE的延长线与CD的延长线 相交于点F.(1)求证:△ABE≌△DFE;(2)连接BD,AF,判断四边形ABDF的形状,并证明你的结论.分析:(1)应用平行四边形的性质证三角形全等.(2)可由AE=DE,再证BE=FE.(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD.∴∠BAD=∠EDF,∠ABE=∠DFE.又∵E是AD的中点,∴AE=DE.∴△ABE≌△DFE(AAS).(2)解:四边形ABDF是平行四边形.证明如下:∵△ABE≌△DFE,∴BE=FE.又AE=ED,∴四边形ABDF是平行四边形.
∵四边形ABCD是平行边形
∴ ∠ A=∠ C, ∠ D=∠ B
∠ A+∠ B= , ∠ A+∠ D= …
∵四边形ABCD是平行边形 ∴OA=OC,OB=OD 温故知新什么样的四边形是平行四边形?我们学过的 两组对边分别平行的 四边形是平行四边形两组对边分别平行∵∴四边形ABCD是平行四边形AB∥CD; AD∥BC 如图,在四边形ABCD中,∠1=∠2,∠3=∠4。四边形ABCD是平行四边形吗?为什么?牛刀小试:操作1:在练习本上放2根互相平行并且相等的细纸条AB、CD,连结AD、BC.四边形ABCD是平行四边形吗?ADBCAB CD表示AB平行且等于CD一组对边平行且相等的四边形是平行四边形. 写出:已知,求证,证明已知:如图,在四边形ABCD中,AB=CD,AB∥CD求证:四边形ABCD是平行四边形验证已知:如图,在四边形ABCD中,AB=CD,AB∥CD求证:四边形ABCD是平行四边形验证证明:连接DB。
∵ AB∥CD,
∴∠CDB= ∠ABD在△CDB与△ABD中
CD=AB(已知)
∠CDB= ∠ABD(已证)
DB=BD(公共边) ∴△CDB≌△ABD(SAS)∴ ∠ADB= ∠CBD(全等三角形的对应角相等)
∴ AD∥BC(内错角相等,两直线平行)
因此,四边形ABCD是平行四边形。一组对边平行且相等的四边形是平行四边形. 几何语言∵∴AD=BC, AD∥BC四边形ABCD是平行四边形 一组对边平行且相等的四边形是平行四边形.一组对边平行且相等 以上活动事实,能用文字语言表达吗? 例1:已知:平行四边形ABCD中,E,F分别是边AD,BC的中点(如图) 求证:EB=DF 证明:∵四边形ABCD
是平行四边形 ∴AD BC ∵ED=1/2AD BF=1/2BC ∴ED BF ∴四边形EBFD是平行四边形
你会几种方法?1.一组对边平行另一组对边相等的四边形是平行四边形吗?
2.如图,AC∥ED,点B在AC上且AB=ED=BC 。
找出图中的平行
四边形.
操作2工具:两对长度分别相等的细纸条. 动手:能否在平面内用这四根细纸条摆成一个平行四边形?试试看!思考:你能说明你们摆出的四边形
是平行四边形吗?平行四边形的对边相等。
逆命题:两组对边分别相等的四边形是平行四边形。已知:四边形ABCD, AB=CD,AD=BC
求证:四边形ABCD是平行四边形证明:
∵ 在△ABC与△CDA中
AB=CD(已知)
AD=BC (已知)
AC=CA (公共边)
∴△ABC≌△CDA(SSS)∴∠1=∠2,∠3=∠4(全等三角形的对应边相等)
∴ AB∥CD,AD∥BC (内错角相等,两直线平行)
∴四边形ABCD是平行四边形BDAC2134验证连结AC,几何语言∵∴AD=BC,DC=AB四边形ABCD是平行四边形以上活动事实,能用文字语言表达吗? 两组对边分别相等的四边形是平行四边形.两组对边分别相等 工人师傅做铝合金窗框分下面三个步骤进行:
(1) 先截出两对符合规格的铝合金窗料(如图①)使AB=CD,EF=GH;
(2)摆放成如图②的四边形,则这时铝合金窗框的形状是 ,
根据的数学道理是: ;
平行四边形两组对边分别相等的四边行是平行四边形驶向胜利的彼岸 如图将两长两短的四根细木条用小钉绞合在一起,做成一个四边形,使等长的木条成为对边.转动这个四边形,使它形状改变,在图形变化的过程中,它一直是一个平行四边形吗?1. 对于四边形ABCD,如果从条件①AB∥CD
②AD∥BC③AB=CD④BC=AD中选出2个,
那么能 说明四边形ABCD是平行四边形的有
_______(填序号,填出符合条件的一种情
况即可)
对角相等的四边形是平行四边形。平行四边形的对角相等的逆命题是:已知四边形ABCD中∠A=∠ C,∠B=∠D,
求证:四边形ABCD是平行四边形。证明:∵∠A+∠B+∠C+∠D=360°且∠C=∠A ,∠D=∠B∴∠A+∠B+∠A+∠B=360°即:2∠A+2∠B=360°2(∠A+∠B)=360°∠A+∠B=180°∴AD∥BC同理:AB∥CD ∴四边形ABCD是平行
四边形对角线互相平分的四边形是平行四边形。平行四边形的对角线互相平分的逆命题是:已知四边形ABCD的对角线AC,BD相交于点O,并且 AO=CO,BO=DO,
求证:四边形ABCD是平行四边形。证明:在△AOB和△COD中∴ △AOB ≌ △COD (SAS)∴AB=CD同理 : AD=CB∴四边形ABCD是平行四边形(两组对边分别相等的四 边形是平行四边形。) 如图,将两根细木条AC、BD的中心重叠,用小钉绞合在一起,用橡皮筋连接木条的顶点,做成一个四边形ABCD,转动两根木条,它一直是一个平行四边形吗?你能证明吗?你又能得到什么结论? 对角线互相平分的四边形是平行四边形你也试一试从边来判定1、两组对边分别平行的四边形是平行四边形(定义) 2、两组对边分别相等的四边形是平行四边形3、一组对边平行且相等的四边形是平行四边形从角来判定两组对角分别相等的四边形是平行四边形从对角线来判定两条对角线互相平分的四边形是平行四边形四、理一理平行四边形的判定方法1、请你识别下列四边形哪些是平行四边形?为什么?⑴⑷
⑶ABCD120°60°5㎝5㎝BADC4.8㎝4.8㎝⑵7.6㎝7.6㎝五、试一试 2、在下列条件中,不能判定四边形是平行四边形的是( )
AB∥CD,AD∥BC
AB=CD,AD=BC
(C)AB∥CD,AB=CD
(D) AB∥CD,AD=BC
(E) AB∥CD, ∠A=∠CD(两组对边分别平行)(两组对边分别相等)(一组对边平行且相等)(两组对角分别相等)开心一练:1.根据下列条件,不能判定一个四边形为平行四边形的是( )
(A)两组对边分别相等
(B)两条对角线互相平分
(C)两条对角线相等
(D)两组对边分别平行C挑战第一关:驶向胜利的彼岸已知:如图求证:四边形MNOP是
平行四边形.数学联想:1、小强给我们了一些什么条件?2、由MO⊥ON联想到什么?边长(含X)、MO⊥ON勾股定理、求x同学们真棒!
这是一道综合运用勾股定理、方程、平行四边形的题目,由这道题我们可以看出,有些几何问题能用代数知识解决。 1、下列条件中,不能判定四边形ABCD是平行四边形的是( )
A、∠A=∠C,∠B=∠D
∠A=∠B=∠C=90
∠A+∠B=180 ,∠B+∠C=180
∠A+∠B=180 ,∠C+∠D=180D2、如图,在平行四边形ABCD的一组对边AD、BC上截取EF=MN,连接EM、FN,EM和FN有怎样的关系?为什么?巩固练习BDACMNEF例1 如图,AB =DC=EF, AD=BC,DE=CF,则图中有哪些互相平行的线段?看谁最快AB ∥ DC∥ EFAD ∥ BCDE ∥ CF例2 已知: 中,M、N、P、Q分别是AB、BC、CD、DA的中点
求证:四边形MNPQ是平行四边形好题大家练例3 如图:四边形ABCD是梯形,在底边AB上求作一点E,使四边形AECD为平行四边形。大显身手大显身手证明一: 四边形ABCD是平行四边形AD ∥ BC且AD =BCEAD= FCBAE=CF
EAD= FCB
AD=BCAED ≌ CFB(SAS)DE=BF四边形BFDE是平行四边形在 AED和 CFB中同理可证:BE=DF4、已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形大显身手4、已知:E、F是平行四边形ABCD对角线AC上的两点,并且AE=CF。
求证:四边形BFDE是平行四边形DOABCEF证明二:作对角线BD,交AC于点O。
∵四边形ABCD是平行四边形
∴ AO=CO,BO=DO
∵AE=CF
∴AO-AE=CO-CF
∴EO=FO
又 BO=DO
∴ 四边形BFDE是平行四边形
大显身手变式1:已知:E、F是平行四边形ABCD对角线AC上的两点,并且
求证:四边形BFDE是平行四边形DABCEFBE∥DF大显身手变式2:已知:E、F是平行四边形ABCD对角线AC上的两点,并且
求证:四边形BFDE是平行四边形DABCEFBE⊥AC于E,DF⊥AC于F大显身手变式3:已知:E、F是平行四边形ABCD对角线AC上的两点,并且
求证:四边形BFDE是平行四边形DABCEFBE=DF动动脑ABCDMNPQO已知:在平行四边形ABCD中,对角线AC 、BD相交于点,M 、 N 、 P、 Q分别是OA 、OB 、OC 、 OD
的中点
求证 四边形MNPQ是平行四边形15 例2(2009年新疆)如图,是四边形的对角线上两点,AF=CE,DF=BE,DF∥BE 求证:(1) (2)四边形ABCD是平行四边形. 证明:(1) ,
问题2:若将这三个点放入到平面直角坐标系中,其中A点坐标为(4,5),B点坐标为(2,0),C点坐标为(7,0),你能求出以A、B、C、D四点为顶点构成平行四边形的第四个顶点点D的坐标吗?活动四:应用定理 昨天初一的李明同学在生物实验室做实验时,不小心碰碎了实验室的一块平行四边形的实验用的玻璃片,只剩下如图所示部分,他想明天星期六回家去割一块赔给学校,带上玻璃剩下部分去玻璃店不安全,于是他想把原来的平行四边形重新在纸上画出来?然后带上图纸去就行了,可原来的平行四边形怎么给它画出来呢?(A,B,C为三顶点,即找出第四个顶点D)生活实际的挑战方法(一)DAB∥CD,AD∥BC∴四边形ABCD是平行四边形方法(二)D两组对边分别相等的四边形是平行四边形方法(三)D方法(四)D两组对角分别相等的四边形是平行四边形方法(五)DO对角线互相平分的四边形是平行四边形已知:如图,在平行四边形ABCD的周长为20cm,O是对角线AC和BD的交点
(1)若△ABC的周长是7cm,求OC的长
(2)若△OAB的周长比△OBC的周长短4cm,求AB的长O4.如图 四边形 ABCD和四边形BEDF都是平行四边形, 请你说明(1) AE=CF的理由
O变式:如图 已知 四边形 ABCD都是平行四边形, AE=CF,请你说明四边形BEDF是平行四边形
拓展训练1 2、已知:AD为△ABC的角平分线,DE∥AB ,在AB上截取BF=AE。
求证:EF=BD
123
3、已知 平行四边形 ABCD中,直线MN // AC,分别交DA延长线于M,DC延长线于N,AB于P,BC于Q。
求证:PM=QN。例2:如图,在△ABC中,AB=14,BC=18,AD是AC边上的中线,求BD的取值范围。两组对边分别相等两组对角分别相等对角线互相平分两组对边分别平行平行四边形的判定方法一组对边平行且相等四边形是平行四边形边角对角线:谈谈你有何收获吧!六、说一说:
1.本节课你学会了几种平行四边形的判定方法2.本节课所学的解决问题的思路是: (2)碰到平行四边形的问题常转化为三角形来解决.(1)解决一个数学问题,常要通过”动手实践”-----”
猜想”-----”验证猜想(证明)”-----”得出结论”2.能够判定四边形ABCD是平行四边形的条件是( ????).A.AB∥CD,AD=BCB.∠A=∠B,∠C=∠DC.AB=CD,AD=BCD.AB=AD,CB=CD答案:C3.如右图所示,四边形ABCD的对角线AC和BD相交于点O,下列判断 正确的是( ????).A.若AO=OC,则四边形ABCD是平行四边形B.若AC=BD,则四边形ABCD是平行四边形C.若AO=BO,CO=DO,则四边形ABCD是平行四边形D.若AO=OC,BO=OD,则四边形ABCD是平行四边形答案:D4.连接三角形两边 ????的线段叫做三角形的中位线.答案:中点5.三角形中位线定理三角形的中位线 ????于三角形的第三边,且等于第三边的 ????.答案:平行 一半6.已知在△ABC中,BC=6 cm,E,F分别是AB,AC的中点,那么EF的长是 ???? cm.答案:37.两条平行线间的任何两条平行线段都 ????.答案:相等1.平行四边形的性质与判定的综合应用【例1】 已知,如图所示,AD为△ABC的中线,E为AC上一点,连接BE 交AD于F,且AE=FE.求证:BF=AC.? 分析:延长AD到N,使DN=AD,构造出平行四边形ABNC求解即可.证明:延长AD到N,使DN=AD,连接BN,CN,∵BD=CD,AD=ND,∴四边形ABNC是平行四边形.∴BN=AC,BN∥AC.∴∠FAE=∠BND.∵AE=FE,∴∠FAE=∠AFE.∵∠AFE=∠BFD,∠FAE=∠BND,∴∠BFD=∠BND,∴BN=BF.∴BF=AC.点拨:有三角形中线时,常延长中线构造平行四边形,然后再利用平行 四边形的性质转化线段或角的相等进行证题.2.三角形中位线定理的运用【例2】 如图所示,已知E,F,G,H分别是线段AB,BD,CD,CA的中点, 求证:四边形EFGH是平行四边形.分析:本题出现多个中点,应想到三角形中位线.E,H分别为AB,AC的中点,那么连接BC后,EH为△ABC的中位线,可 利用中位线证明.证明:连接BC,AD,∵H为AC的中点,E为AB的中点,∴EH∥BC,EH=?BC.又∵G为CD的中点,F为BD的中点,∴GF∥BC,GF=?BC.∴EH∥GF且EH=GF.∴四边形EFGH为平行四边形.点拨:当题目中已知线段的中点时,一般应考虑运用三角形的中位线 定理,取中点构造中位线是作辅助线的常用方法.1.下列条件不能判断四边形ABCD是平行四边形的是( ????).A.∠A=∠C,∠B=∠D ????B.AD=BC,AB=CDC.AB=CD,AD∥BC ????D.AB∥CD,AD∥BC解析:一组对边平行且相等的四边形是平行四边形,故C错误.答案:C2.小明的爸爸在钉制平行四边形框架时,采用了一种方法:将两根木 条AC,BD的中点重叠,并用钉子固定,则四边形ABCD就是平行四边 形,这种方法的依据是( ????).A.两组对边分别平行的四边形是平行四边形B.对角线互相平分的四边形是平行四边形C.一组对边平行且相等的四边形是平行四边形D.两组对角分别相等的四边形是平行四边形答案:B3.(2011·山东德州中考)如图,D,E,F分别为△ABC三边的中点,则图中 平行四边形的个数为 ????.解析:由三角形的中位线定理得,DE∥AC,DF∥BC,EF∥AB.所以由 平行四边形的定义得,四边形ADEF、四边形BEFD、四边形ECFD 是平行四边形.答案:34.在四边形ABCD中,AB∥CD,要使四边形ABCD为平行四边形,则可 添加的条件为 ????.(填一个即可)答案:答案不唯一,如AB=CD或∠A=∠C或AD∥BC5.在?ABCD中,分别以AD,BC为边向内作等边△ADE和等边△ BCF,连接BE,DF.求证:四边形BEDF是平行四边形.证明:∵四边形ABCD是平行四边形,∴CD=AB,AD=CB,∠DAB=∠BCD.又∵△ADE和△CBF都是等边三角形,∴DE=BF,AE=CF,∠DAE=∠BCF=60°.∵∠DCF=∠BCD-∠BCF,∠BAE=∠DAB-∠DAE,∴∠DCF=∠ BAE.∴△DCF≌△BAE(SAS).∴DF=BE.∴四边形BEDF是平行四边形.6.如图,在?ABCD中,点E是AD的中点,BE的延长线与CD的延长线 相交于点F.(1)求证:△ABE≌△DFE;(2)连接BD,AF,判断四边形ABDF的形状,并证明你的结论.分析:(1)应用平行四边形的性质证三角形全等.(2)可由AE=DE,再证BE=FE.(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD.∴∠BAD=∠EDF,∠ABE=∠DFE.又∵E是AD的中点,∴AE=DE.∴△ABE≌△DFE(AAS).(2)解:四边形ABDF是平行四边形.证明如下:∵△ABE≌△DFE,∴BE=FE.又AE=ED,∴四边形ABDF是平行四边形.
