华东师大版数学九年级上册 23.3.3 相似三角形的性质课件课件(共22张PPT)
文档属性
| 名称 | 华东师大版数学九年级上册 23.3.3 相似三角形的性质课件课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-02 00:00:00 | ||
图片预览





文档简介
(共22张PPT)
23.3 相似三角形
第4课时:相似三角形的性质
华东师大版九年级数学上册
1. 相似三角形的判定方法有哪些?
2. 相似三角形的性质有哪些?
3. 全等三角形有哪些性质?
一. 温故而知新
全等三角形与相似三角形性质比较
全等三角形 相似三角形
对应边相等 对应边的比等于相似比
对应角相等 对应角相等
对应高相等 对应高……
对应中线相等 对应中线……
对应角平分线相等 对应角平分线……
周长相等 周长……
面积相等 面积……
展开想象的翅膀
二.问题探究
画一画:
请你在课本后面的方格纸图中,画出两个相似但不全等的三角形,再画一组对应高。
C1
B1
A1
A
C
B
D
D1
量一量:
你画的两个相似三角形的相似比是多少?对应高AD与A1D1的比是多少?相似比与对应高的比相等吗?
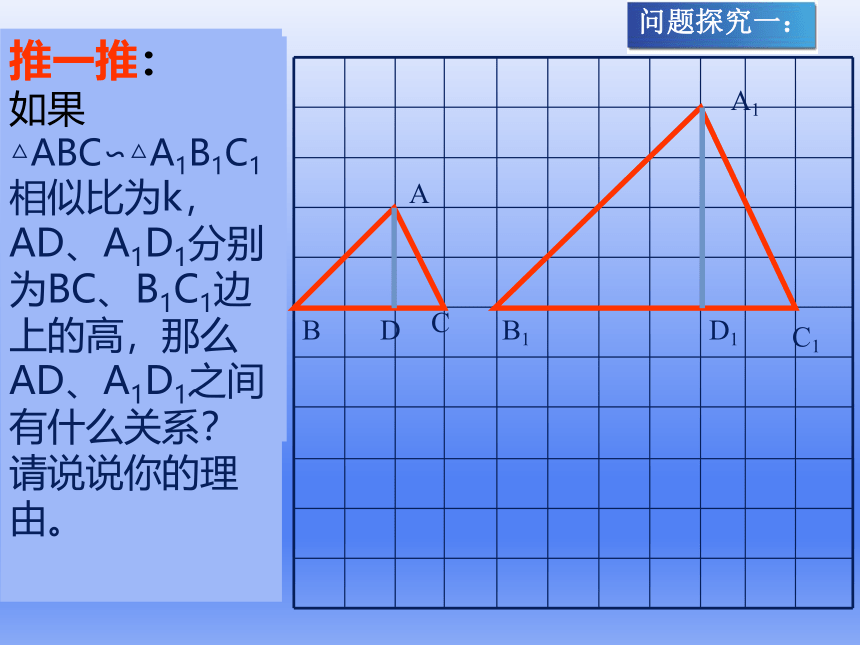
推一推:
如果△ABC∽△A1B1C1相似比为k, AD、A1D1分别为BC、B1C1边上的高,那么AD、A1D1之间有什么关系?请说说你的理由。
问题探究一:
∴ ∠B =∠B1
又 ∠ADB=∠A1D1B1 = 90°,
∴ △ABC∽ △A1B1C1
C1
B1
A1
A
C
B
D
D1
已知:如图,△ABC∽ △A1B1C1, △ABC与 △A1B1C1的相似比是k, AD、A1D1是对应高。
求证:
∵ △ABC∽ ,
证明:
△
A1B1C1
C1
B1
A1
A
C
B
D
D1
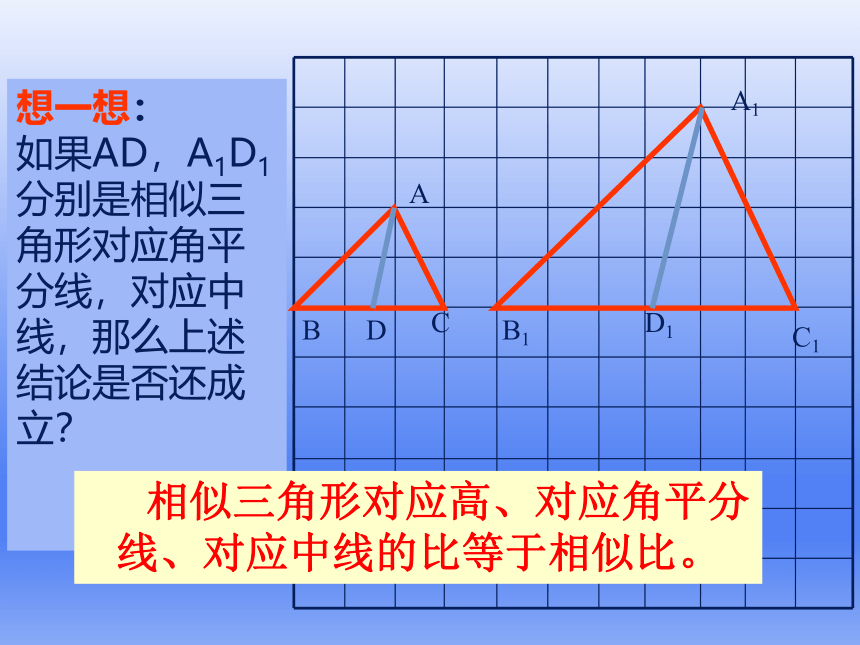
想一想:
如果AD,A1D1分别是相似三角形对应角平分线,对应中线,那么上述结论是否还成立?
相似三角形对应高、对应角平分线、对应中线的比等于相似比。
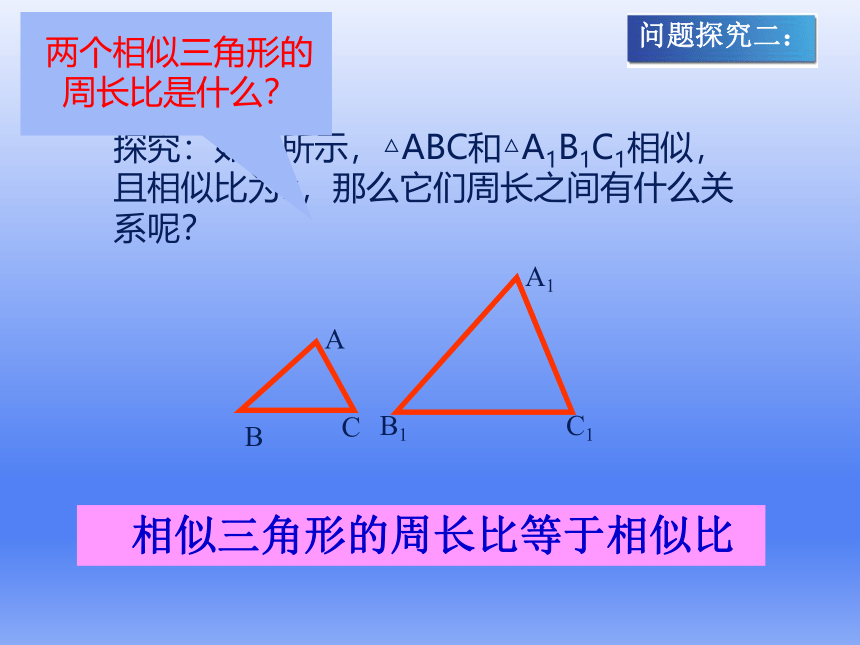
探究:如图所示,△ABC和△A1B1C1相似,且相似比为k,那么它们周长之间有什么关系呢?
两个相似三角形的周长比是什么?
相似三角形的周长比等于相似比
C1
B1
A1
A
C
B
问题探究二:
结论
通过前面的实验、探索、推理,我们得到相似三角形有如下性质:
.相似三角形的周长比等于相似比.
.相似三角形对应高、对应中线、对应角平分线的比等于相似比.
做一做
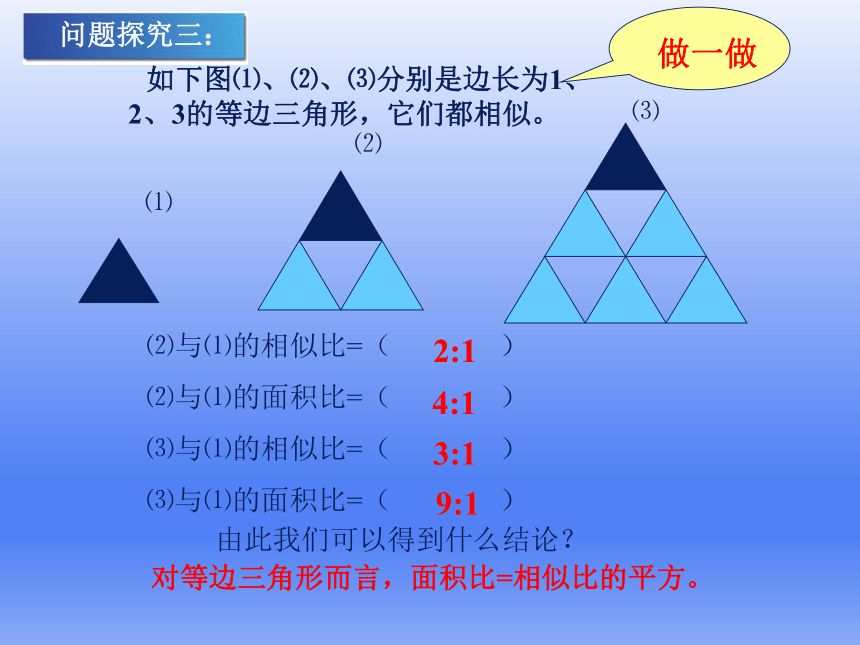
如下图⑴、⑵、⑶分别是边长为1、2、3的等边三角形,它们都相似。
⑴
⑵
⑶
⑵与⑴的相似比=( )
⑵与⑴的面积比=( )
⑶与⑴的相似比=( )
⑶与⑴的面积比=( )
由此我们可以得到什么结论?
对等边三角形而言,面积比=相似比的平方。
2:1
4:1
3:1
9:1
问题探究三:
动动你聪明的
脑子,想一想
上述结论是否适用于一般的相似三角形?
A
B
C
A′
B′
C′
D
D′
证明:
分别过A、A′,
作AD⊥BC于D,
∵
∴
∴
∴
相似三角形的面积比等于相似比的平方。
∽ △
△
结论
我们从特殊的等边三角形入手,发展到一般的三角形,
经过实验探究,推理探究,得出以下结论:
.相似三角形面积比等于相似比的平方.
例:小王有一块三角形余料ABC,它的边BC=60cm,高线AD=40cm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上。
A
B
C
S
R
E
P
D
Q
(1) △ ASR与△ ABC相似吗?为什么?
(2)求正方形SPQR的面积。
三. 知识运用
例 题 解 析
(1)△ASR与△ABC相似吗 为什么
(2)求正方形PQRS的面积.
分析:(1) △ASR∽△ABC.理由是:
四边形PQRS是正方形
RS∥BC
∠ASR= ∠B
∠ARS= ∠C
△ASR∽△ABC.
例 题 解 析
A
B
C
S
R
E
P
D
Q
40
60
(1)△ASR与△ABC相似吗 为什么
(2)求正方形PQRS的面积.
分析:
(2)由(1)可知, △ASR∽△ABC.
设正方形PQRS的边长为x cm, 则AE=(40-x)cm,
解得,x=24.
所以正方形PQRS的面积为576cm2.
(相似三角形对应高的比等于相似比)
A
B
C
S
R
E
P
D
Q
40
60
例 题 解 析
1、相似三角形对应边的比为3∶5 ,那么相似比为_________,对应角的角平分线的比为______,对应边的中线比为_______,周长的比为_____,面积的比为_______。
3∶5
3∶5
3∶5
9∶25
3∶5
2、两个相似三角形对应的中线长分别是6cm和18cm,若较大三角形的周长是42cm,面积是12cm2,则较小三角形的周长是 cm,面积 cm2。
14
四. 巩固练习
3. 如图,DF∥EG∥BC,且AD=DE=EB,
则△ABC被分成的三部分的面积比S1:S2:S3= 。
S3
B
E
D
A
S1
F
G
C
S2
S3
B
E
D
A
S1
解:∵DF∥EG∥BC,
∴△ADF∽△AEG∽△ABC,
又∵AD=DE=EB,
∴三个三角形的相似比是1:2:3,
∴面积的比是1:4:9,
设△ADF的面积是a,
则△AEG与△ABC的面积分别是4a,9a,
∴S2=3a,S3=5a,
则S1:S2:S3=1:3:5.
全等三角形 相似三角形
对应边相等 对应边的比等于相似比
对应角相等 对应角相等
对应高相等 对应高的比等于相似比
对应中线相等 对应中线的比等于相似比
对应角平分线相等 对应角平分线的比等于相似比
周长相等 周长的比等于相似比
面积相等 面积的比等于相似比的平方
相似三角形的性质
五. 小结与复习
1、两个矩形相似,它们的对角线之比是1:3,那么它们的相似比是 ,周长比是 ,面积比是 .
2、若两个相似三角形的相似比是3:5,其中第一个三角形的周长为21cm,则第二个三角形的周长为 cm.
3、如果把一个三角形每条边的长都扩大为原来的5倍,那么它的周长扩大为原来的 倍,而面积扩大为原来的 倍.
4、如图,已知△ABC∽△ADE,且BC=2DE,则△ADE与四边形BCDE的面积比为( )
(A)1:2 (B)1:3 (C)1;4 (D)1:5
A
B
C
D
E
六. 自我测试
思考题:
A
B
D
C
E
在△ABC中,BC=m,DE∥BC,交AB于E,交AC于D, ,求DE的长度。
1.书p74,练习题1.2.
2.同步练习册23.3(四)
七. 课后作业
23.3 相似三角形
第4课时:相似三角形的性质
华东师大版九年级数学上册
1. 相似三角形的判定方法有哪些?
2. 相似三角形的性质有哪些?
3. 全等三角形有哪些性质?
一. 温故而知新
全等三角形与相似三角形性质比较
全等三角形 相似三角形
对应边相等 对应边的比等于相似比
对应角相等 对应角相等
对应高相等 对应高……
对应中线相等 对应中线……
对应角平分线相等 对应角平分线……
周长相等 周长……
面积相等 面积……
展开想象的翅膀
二.问题探究
画一画:
请你在课本后面的方格纸图中,画出两个相似但不全等的三角形,再画一组对应高。
C1
B1
A1
A
C
B
D
D1
量一量:
你画的两个相似三角形的相似比是多少?对应高AD与A1D1的比是多少?相似比与对应高的比相等吗?
推一推:
如果△ABC∽△A1B1C1相似比为k, AD、A1D1分别为BC、B1C1边上的高,那么AD、A1D1之间有什么关系?请说说你的理由。
问题探究一:
∴ ∠B =∠B1
又 ∠ADB=∠A1D1B1 = 90°,
∴ △ABC∽ △A1B1C1
C1
B1
A1
A
C
B
D
D1
已知:如图,△ABC∽ △A1B1C1, △ABC与 △A1B1C1的相似比是k, AD、A1D1是对应高。
求证:
∵ △ABC∽ ,
证明:
△
A1B1C1
C1
B1
A1
A
C
B
D
D1
想一想:
如果AD,A1D1分别是相似三角形对应角平分线,对应中线,那么上述结论是否还成立?
相似三角形对应高、对应角平分线、对应中线的比等于相似比。
探究:如图所示,△ABC和△A1B1C1相似,且相似比为k,那么它们周长之间有什么关系呢?
两个相似三角形的周长比是什么?
相似三角形的周长比等于相似比
C1
B1
A1
A
C
B
问题探究二:
结论
通过前面的实验、探索、推理,我们得到相似三角形有如下性质:
.相似三角形的周长比等于相似比.
.相似三角形对应高、对应中线、对应角平分线的比等于相似比.
做一做
如下图⑴、⑵、⑶分别是边长为1、2、3的等边三角形,它们都相似。
⑴
⑵
⑶
⑵与⑴的相似比=( )
⑵与⑴的面积比=( )
⑶与⑴的相似比=( )
⑶与⑴的面积比=( )
由此我们可以得到什么结论?
对等边三角形而言,面积比=相似比的平方。
2:1
4:1
3:1
9:1
问题探究三:
动动你聪明的
脑子,想一想
上述结论是否适用于一般的相似三角形?
A
B
C
A′
B′
C′
D
D′
证明:
分别过A、A′,
作AD⊥BC于D,
∵
∴
∴
∴
相似三角形的面积比等于相似比的平方。
∽ △
△
结论
我们从特殊的等边三角形入手,发展到一般的三角形,
经过实验探究,推理探究,得出以下结论:
.相似三角形面积比等于相似比的平方.
例:小王有一块三角形余料ABC,它的边BC=60cm,高线AD=40cm,要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上。
A
B
C
S
R
E
P
D
Q
(1) △ ASR与△ ABC相似吗?为什么?
(2)求正方形SPQR的面积。
三. 知识运用
例 题 解 析
(1)△ASR与△ABC相似吗 为什么
(2)求正方形PQRS的面积.
分析:(1) △ASR∽△ABC.理由是:
四边形PQRS是正方形
RS∥BC
∠ASR= ∠B
∠ARS= ∠C
△ASR∽△ABC.
例 题 解 析
A
B
C
S
R
E
P
D
Q
40
60
(1)△ASR与△ABC相似吗 为什么
(2)求正方形PQRS的面积.
分析:
(2)由(1)可知, △ASR∽△ABC.
设正方形PQRS的边长为x cm, 则AE=(40-x)cm,
解得,x=24.
所以正方形PQRS的面积为576cm2.
(相似三角形对应高的比等于相似比)
A
B
C
S
R
E
P
D
Q
40
60
例 题 解 析
1、相似三角形对应边的比为3∶5 ,那么相似比为_________,对应角的角平分线的比为______,对应边的中线比为_______,周长的比为_____,面积的比为_______。
3∶5
3∶5
3∶5
9∶25
3∶5
2、两个相似三角形对应的中线长分别是6cm和18cm,若较大三角形的周长是42cm,面积是12cm2,则较小三角形的周长是 cm,面积 cm2。
14
四. 巩固练习
3. 如图,DF∥EG∥BC,且AD=DE=EB,
则△ABC被分成的三部分的面积比S1:S2:S3= 。
S3
B
E
D
A
S1
F
G
C
S2
S3
B
E
D
A
S1
解:∵DF∥EG∥BC,
∴△ADF∽△AEG∽△ABC,
又∵AD=DE=EB,
∴三个三角形的相似比是1:2:3,
∴面积的比是1:4:9,
设△ADF的面积是a,
则△AEG与△ABC的面积分别是4a,9a,
∴S2=3a,S3=5a,
则S1:S2:S3=1:3:5.
全等三角形 相似三角形
对应边相等 对应边的比等于相似比
对应角相等 对应角相等
对应高相等 对应高的比等于相似比
对应中线相等 对应中线的比等于相似比
对应角平分线相等 对应角平分线的比等于相似比
周长相等 周长的比等于相似比
面积相等 面积的比等于相似比的平方
相似三角形的性质
五. 小结与复习
1、两个矩形相似,它们的对角线之比是1:3,那么它们的相似比是 ,周长比是 ,面积比是 .
2、若两个相似三角形的相似比是3:5,其中第一个三角形的周长为21cm,则第二个三角形的周长为 cm.
3、如果把一个三角形每条边的长都扩大为原来的5倍,那么它的周长扩大为原来的 倍,而面积扩大为原来的 倍.
4、如图,已知△ABC∽△ADE,且BC=2DE,则△ADE与四边形BCDE的面积比为( )
(A)1:2 (B)1:3 (C)1;4 (D)1:5
A
B
C
D
E
六. 自我测试
思考题:
A
B
D
C
E
在△ABC中,BC=m,DE∥BC,交AB于E,交AC于D, ,求DE的长度。
1.书p74,练习题1.2.
2.同步练习册23.3(四)
七. 课后作业
