华东师大版数学九年级上册 第24章 解直角三角形复习课课件(共10张PPT)
文档属性
| 名称 | 华东师大版数学九年级上册 第24章 解直角三角形复习课课件(共10张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 831.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-02 14:23:19 | ||
图片预览


文档简介
(共10张PPT)
华师大版九年级
数学(上)
第24章 解直角三角形
(复习课)
【复习目标】
一、回顾测量的知识
1.利用三角形相似可以设计方案测量不可到达的
两地之间的距离,或不可直接测量出的物体
的高度和宽度.
2.勾股定理在测量问题中的应用.
二、回顾直角三角形的性质.
三、回顾锐角三角函数的定义、特殊角的三角函数值.
四、回顾解直角三角形的定义、解直角三角形的实际
应用.体会数形结合思想、转化思想、方程思想
【复习指导】带着以下问题进行复习(5分钟)
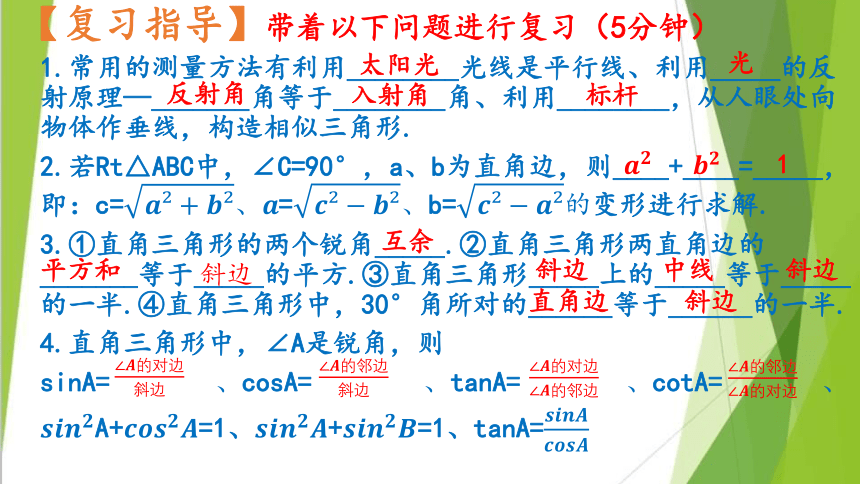
1.常用的测量方法有利用________光线是平行线、利用_____的反射原理—_______角等于________角、利用________,从人眼处向物体作垂线,构造相似三角形.
2.若Rt△ABC中,∠C=90°,a、b为直角边,则____+____=_____,即:c==b=变形进行求解.
3.①直角三角形的两个锐角_____.②直角三角形两直角边的_______等于_____的平方.③直角三角形_____上的_____等于_____的一半.④直角三角形中,30°角所对的______等于______的一半.
4.直角三角形中,∠A是锐角,则
sinA=cosA=tanA=cotA=
A+=1、+=1、tanA=
太阳光
光
反射角
入射角
标杆
1
互余
平方和
斜边
中线
斜边
直角边
斜边
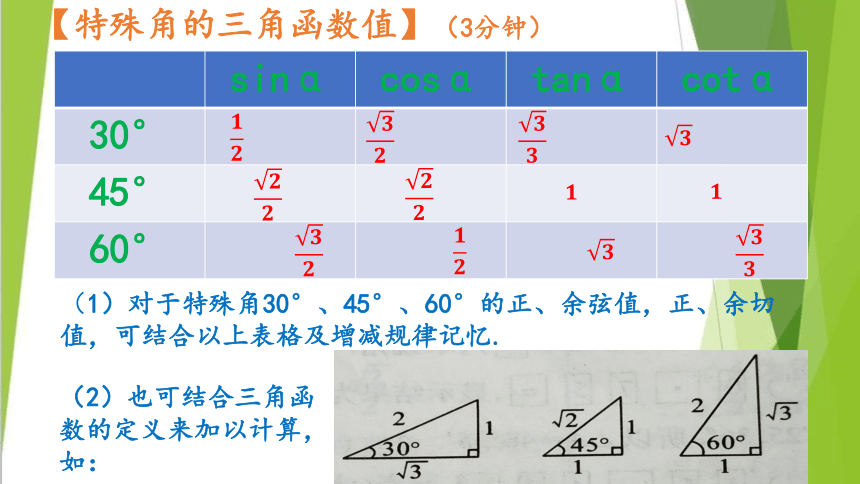
【特殊角的三角函数值】(3分钟)
sinα cosα tanα cotα
30°
45°
60°
(1)对于特殊角30°、45°、60°的正、余弦值,正、余切值,可结合以上表格及增减规律记忆.
(2)也可结合三角函数的定义来加以计算,如:
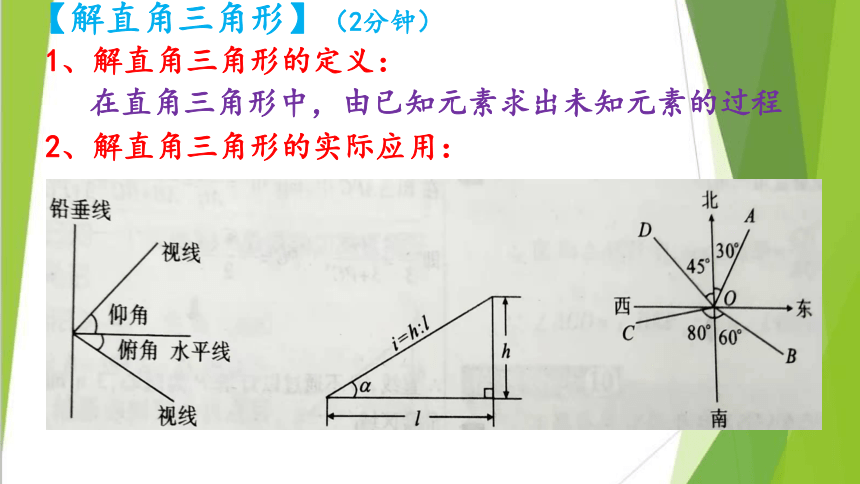
【解直角三角形】(2分钟)
1、解直角三角形的定义:
2、解直角三角形的实际应用:
在直角三角形中,由已知元素求出未知元素的过程
【复习巩固】(结合已学知识细心解答)
1、(配练P74第3题)如图所示,为测量某建筑物AB的高度,在平地C处测得建筑物顶端A的仰角为30°,沿CD方向前进12m到达D处,在D处测得建筑物顶端A的仰角为45°,求建筑物AB的高度.
解:在Rt △ABC中,
设建筑物AB的高度为x m,由题意可知:
BD=AB=x m,
则:tan30°=,即
:
答:建筑物AB的高度为
方法总结:未知元素可用设未知数的方法,结合锐角三角函数
解直接三角形的来解决.
2.(配练P74第7题)河堤横断面如图所示,堤高BC=5m,迎水坡AB的坡比是1:(坡比是坡面的铅垂高度BC与水平宽度AC之比),求AC的长.
解:在Rt△ABC中
∵BC=5m
BC:AC=1:
∴
∴AC= m
方法总结:涉及坡度或坡比()、坡面的铅垂高度()、水平长度()这些元素的求法,可根据坡度(或坡比)公式:
= = tan来求解.
3. 如图所示,一艘船向正北行,在A处看到灯塔S在船的北偏东30°的方向上,航行12海里到达B点,在B处看到灯塔S在船的北偏东60°的方向上,求此船继续沿正北方向航行的过程中距灯塔S的最近距离.
解:作SC垂直于AB于C
∵∠A=30°
∴∠S=30°,AB=SB=12海里
在Rt △SCB中
∵∠SBC=60°,SB=12海里
∴sin60°=
即SC=12×6海里
∴此船继续沿正北方向航行的过程中距灯塔S的最近距离是6海里.
方法总结:先由题意构建直角三角形,再应用锐角三角函数来解决
【小结与反思】
1、解直角三角形是中考的重要内容之一,直角三角形边、角关
系的知识是解直角三角形的基础;解直角三角形时,要注意
三角函数的选取,避免计算复杂;在解题时,若求解的边、
角不在直角三角形中,应先添加辅助线,构造直角三角形.
2、与解直角三角形有关的应用问题逐步成为命题的热点,主要
有轮船、卫星定位问题、堤坝工程问题、建筑测量问题、高
度测量问题等,解决各类应用问题时要注意把握各类图形的
特征及解法.
反思:用“割补法”构造直角三角形求解的技巧
有关非直角三角形、四边形,尤其是等腰三角形、梯形等问题,一般通过作辅助线(主要是高线或垂线)对图形进行“割”或“补”,构造直角三角形.
【课后作业】
1、运用已学知识认真、仔细完成配套练习P74页章检测题,注意运算、书写和格式正确性.
2、按时、独立完成作业.
华师大版九年级
数学(上)
第24章 解直角三角形
(复习课)
【复习目标】
一、回顾测量的知识
1.利用三角形相似可以设计方案测量不可到达的
两地之间的距离,或不可直接测量出的物体
的高度和宽度.
2.勾股定理在测量问题中的应用.
二、回顾直角三角形的性质.
三、回顾锐角三角函数的定义、特殊角的三角函数值.
四、回顾解直角三角形的定义、解直角三角形的实际
应用.体会数形结合思想、转化思想、方程思想
【复习指导】带着以下问题进行复习(5分钟)
1.常用的测量方法有利用________光线是平行线、利用_____的反射原理—_______角等于________角、利用________,从人眼处向物体作垂线,构造相似三角形.
2.若Rt△ABC中,∠C=90°,a、b为直角边,则____+____=_____,即:c==b=变形进行求解.
3.①直角三角形的两个锐角_____.②直角三角形两直角边的_______等于_____的平方.③直角三角形_____上的_____等于_____的一半.④直角三角形中,30°角所对的______等于______的一半.
4.直角三角形中,∠A是锐角,则
sinA=cosA=tanA=cotA=
A+=1、+=1、tanA=
太阳光
光
反射角
入射角
标杆
1
互余
平方和
斜边
中线
斜边
直角边
斜边
【特殊角的三角函数值】(3分钟)
sinα cosα tanα cotα
30°
45°
60°
(1)对于特殊角30°、45°、60°的正、余弦值,正、余切值,可结合以上表格及增减规律记忆.
(2)也可结合三角函数的定义来加以计算,如:
【解直角三角形】(2分钟)
1、解直角三角形的定义:
2、解直角三角形的实际应用:
在直角三角形中,由已知元素求出未知元素的过程
【复习巩固】(结合已学知识细心解答)
1、(配练P74第3题)如图所示,为测量某建筑物AB的高度,在平地C处测得建筑物顶端A的仰角为30°,沿CD方向前进12m到达D处,在D处测得建筑物顶端A的仰角为45°,求建筑物AB的高度.
解:在Rt △ABC中,
设建筑物AB的高度为x m,由题意可知:
BD=AB=x m,
则:tan30°=,即
:
答:建筑物AB的高度为
方法总结:未知元素可用设未知数的方法,结合锐角三角函数
解直接三角形的来解决.
2.(配练P74第7题)河堤横断面如图所示,堤高BC=5m,迎水坡AB的坡比是1:(坡比是坡面的铅垂高度BC与水平宽度AC之比),求AC的长.
解:在Rt△ABC中
∵BC=5m
BC:AC=1:
∴
∴AC= m
方法总结:涉及坡度或坡比()、坡面的铅垂高度()、水平长度()这些元素的求法,可根据坡度(或坡比)公式:
= = tan来求解.
3. 如图所示,一艘船向正北行,在A处看到灯塔S在船的北偏东30°的方向上,航行12海里到达B点,在B处看到灯塔S在船的北偏东60°的方向上,求此船继续沿正北方向航行的过程中距灯塔S的最近距离.
解:作SC垂直于AB于C
∵∠A=30°
∴∠S=30°,AB=SB=12海里
在Rt △SCB中
∵∠SBC=60°,SB=12海里
∴sin60°=
即SC=12×6海里
∴此船继续沿正北方向航行的过程中距灯塔S的最近距离是6海里.
方法总结:先由题意构建直角三角形,再应用锐角三角函数来解决
【小结与反思】
1、解直角三角形是中考的重要内容之一,直角三角形边、角关
系的知识是解直角三角形的基础;解直角三角形时,要注意
三角函数的选取,避免计算复杂;在解题时,若求解的边、
角不在直角三角形中,应先添加辅助线,构造直角三角形.
2、与解直角三角形有关的应用问题逐步成为命题的热点,主要
有轮船、卫星定位问题、堤坝工程问题、建筑测量问题、高
度测量问题等,解决各类应用问题时要注意把握各类图形的
特征及解法.
反思:用“割补法”构造直角三角形求解的技巧
有关非直角三角形、四边形,尤其是等腰三角形、梯形等问题,一般通过作辅助线(主要是高线或垂线)对图形进行“割”或“补”,构造直角三角形.
【课后作业】
1、运用已学知识认真、仔细完成配套练习P74页章检测题,注意运算、书写和格式正确性.
2、按时、独立完成作业.
