苏科版九年级上册3.3.7 菱形的判定
文档属性
| 名称 | 苏科版九年级上册3.3.7 菱形的判定 |  | |
| 格式 | zip | ||
| 文件大小 | 817.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-02 19:42:06 | ||
图片预览





文档简介
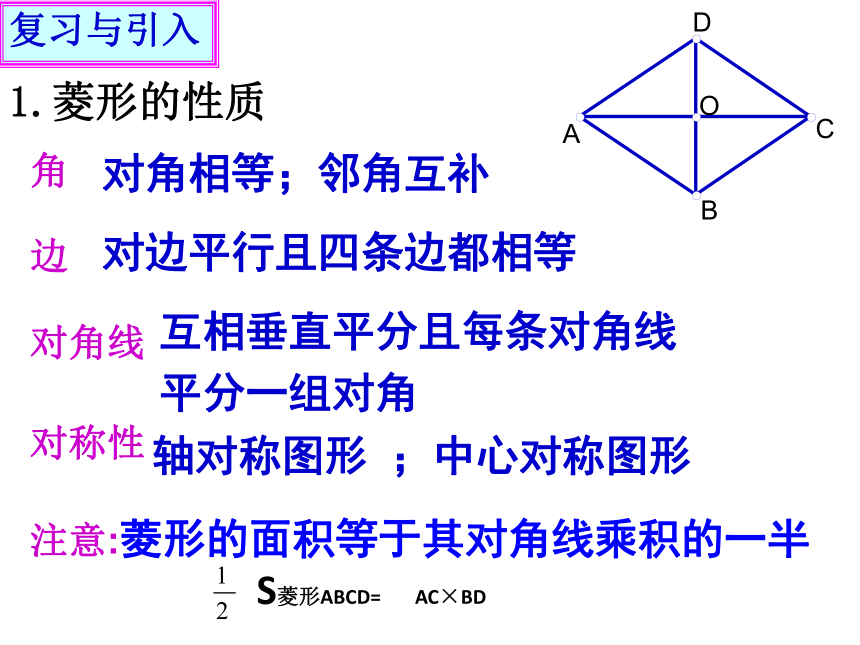
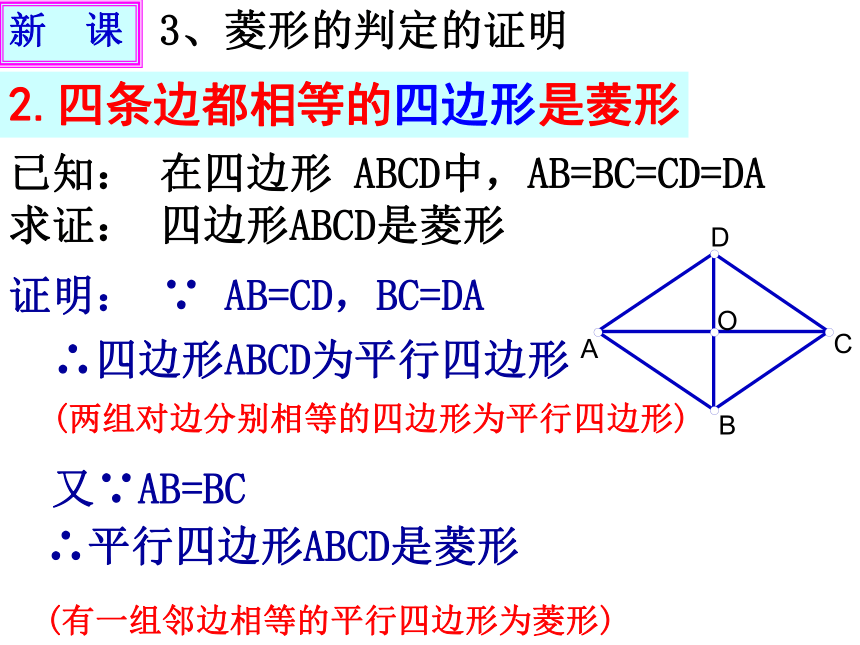
课件32张PPT。1.3.7 菱形的判定1.菱形的性质复习与引入角对角相等;邻角互补边对边平行且四条边都相等对角线互相垂直平分且每条对角线
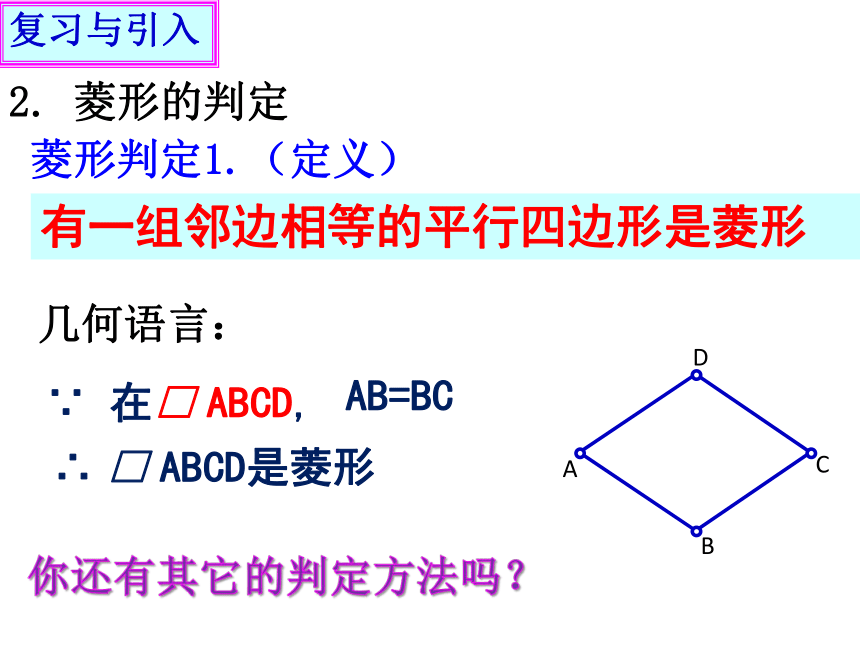
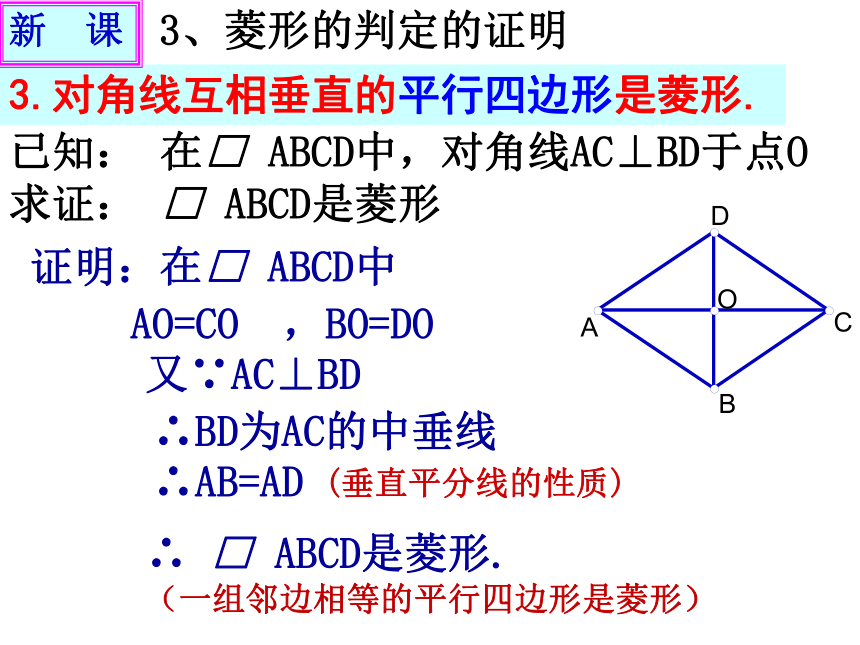
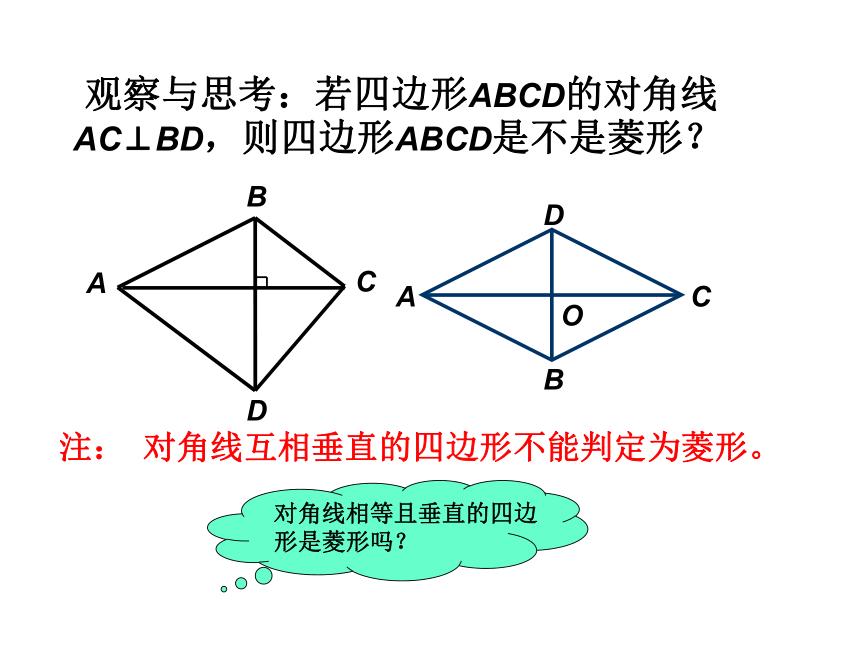
平分一组对角对称性轴对称图形 ;中心对称图形 注意:菱形的面积等于其对角线乘积的一半菱形判定1.(定义)有一组邻边相等的平行四边形是菱形∵ 在□ ABCD,AB=BC∴ □ ABCD是菱形几何语言:2. 菱形的判定你还有其它的判定方法吗?复习与引入∴ □ ABCD是菱形. (一组邻边相等的平行四边形是菱形)3.对角线互相垂直的平行四边形是菱形.证明:在□ ABCD中又∵AC⊥BD∴BD为AC的中垂线∴AB=ADAO=CO ,BO=DO已知: 在□ ABCD中,对角线AC⊥BD于点O 求证: □ ABCD是菱形(垂直平分线的性质)新 课3、菱形的判定的证明 观察与思考:若四边形ABCD的对角线AC⊥BD,则四边形ABCD是不是菱形?注: 对角线互相垂直的四边形不能判定为菱形。 你能用直尺和圆规作一个菱形吗?请作图并说明理由。思考与探索2.四条边都相等的四边形是菱形证明: ∵ AB=CD,BC=DA∴四边形ABCD为平行四边形又∵AB=BC∴平行四边形ABCD是菱形已知: 在四边形 ABCD中,AB=BC=CD=DA 求证: 四边形ABCD是菱形(两组对边分别相等的四边形为平行四边形)(有一组邻边相等的平行四边形为菱形)新 课3、菱形的判定的证明菱形的判定:一组邻边相等的平行四边形是菱形.对角线互相垂直的平行四边形是菱形.四条边都相等的四边形是菱形.小结:练习1、已知 □ ABCD的对角线AC、BD相交于点O,分别添加下列条件:(1)∠ABC=900 (2)AC ⊥BD (3)AB=BC (4)AC平分∠BAD (5)AO=DO 使得四边形ABCD是菱形的条件的序号有__________
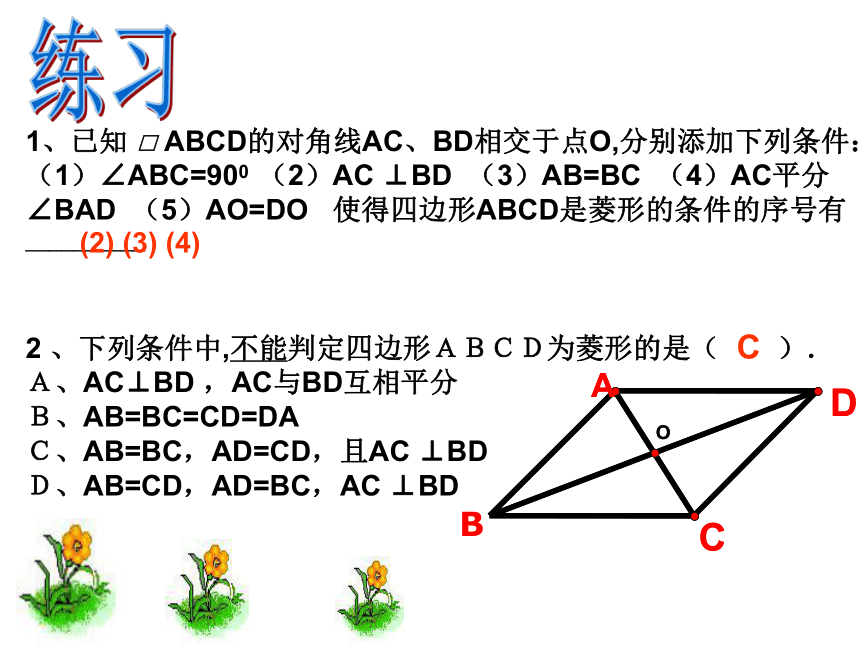
2 、下列条件中,不能判定四边形ABCD为菱形的是( ).
A、AC⊥BD ,AC与BD互相平分
B、AB=BC=CD=DA
C、AB=BC,AD=CD,且AC ⊥BD
D、AB=CD,AD=BC,AC ⊥BD
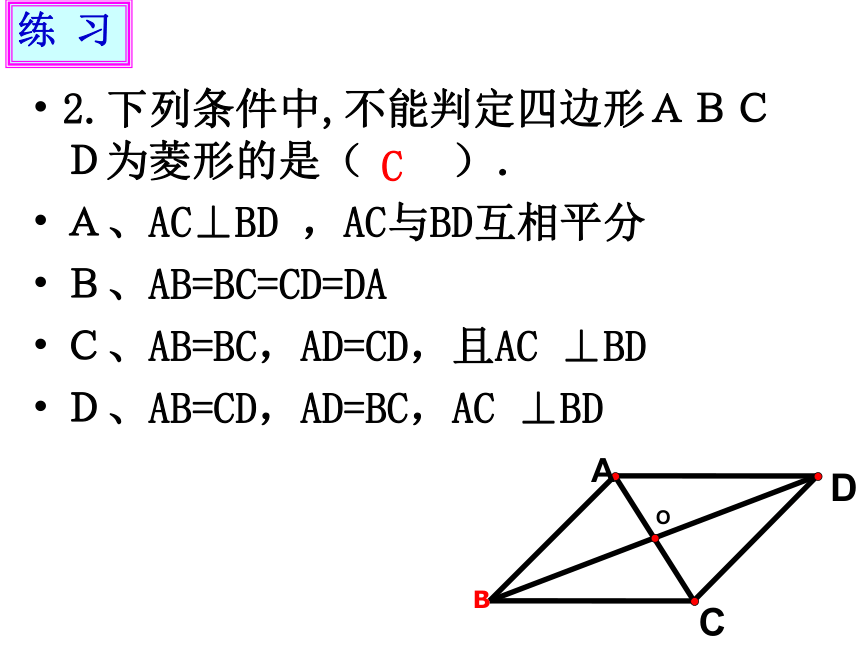
B(2) (3) (4)C2.下列条件中,不能判定四边形ABCD为菱形的是( ).
A、AC⊥BD ,AC与BD互相平分
B、AB=BC=CD=DA
C、AB=BC,AD=CD,且AC ⊥BD
D、AB=CD,AD=BC,AC ⊥BDB练 习C(4)有一组邻边相等的四边形是菱形; 1、判断下列命题是否正确,并说明理由:(1)对角线互相平分且邻边相等的四边
形是菱形;(2)两组对边分别平行且一组邻边相等
的四边形是菱形;(3)邻角相等的四边形是菱形;练 习XX(8)一条对角线平分一个内角的平行四边形是菱形。 (5)两组对角分别相等且对角线互相垂直的四边形是菱形;(6)对角线互相垂直的四边形是菱形;(7)对角线互相垂直平分的四边形是菱形;练 习X判断下列说法是否正确:1.有一条对角线平分一组对角的四边形是菱形3.对角线相等且互相平分的四边形是菱形矩形2.对角线互相垂直,且一条对角线平分一组对角的四边形是菱形4.对角线互相垂直平分的四边形是菱形邻边相等对角线互相垂直AD=DC AC⊥BD 四边相等AD=DC=CB=BA对角线互相垂直平分AC⊥BD,AO=CO,BO=DO归 纳
例2:如图,已知AD平分∠BAC,DE//AC,DF//AB,AE=5.
(1)判断四边形AEDF的形状?
(2)四边形AEDF的周长为多少?
例1.已知:平行四边形ABCD的对角线AC的垂直平分线与边AD,BC分别交于E,F。 求证:四边形AFCE是菱形。ABEDCFO12证明:平行四边形ABCD中AD∥BC∴∠1=∠2,∠3=∠443EF垂直平分AC∴AO=CO,AF=CF,AE=CE∴ △AOF≌△COE∴ AF=CE∴ AF=CF=AE=CE∴四边形AFCE是菱形四条边都相等的四边形是菱形例1.已知:平行四边形ABCD的对角线AC的垂直平分线与边AD,BC分别交于E,F。 求证:四边形AFCE是菱形。ABEDCFO12证明:平行四边形ABCD中AD∥BC∴∠1=∠2,∠3=∠443EF垂直平分AC∴AO=CO,AF=CF,∴ △AOF≌△COE∴ AF=CE∴平行四边形四边形AFCE是菱形又AF∥CE∴四边形AFCE是平行四边形一组邻边相等的平行四边形是菱形例1.已知:平行四边形ABCD的对角线AC的垂直平分线与边AD,BC分别交于E,F。 求证:四边形AFCE是菱形。ABEDCFO123’证明:平行四边形ABCD中AD∥BC∴∠1=∠2,∠3=∠443EF垂直平分AC∴AO=CO,AC⊥EF,∴ △AOF≌△COE∴ AF=CE∴平行四边形四边形AFCE是菱形又AF∥CE∴四边形AFCE是平行四边形对角线互相垂直的平行四边形是菱形例3.如图,已知AD是△ABC的角平分线,
DE∥AC交AB于E,DF∥AB交AC于F,
求证:AD⊥EF。
1 2
3
证明:∵DE∥AC ,DF∥AB∴四边形AEDF是平行四边形∴ ∠2=∠3∵ AD是△ABC的角平分线∴ ∠1=∠2∴ ∠1=∠3∴ AE=DE∴ □AEDF是菱形∴ AD⊥EF∵DE∥AC 例1、把两张等宽的纸条交叉重叠在一起,试探究重叠部分ABCD的形状,并说明理由。
ACDBABCDEF12解:重叠部分为菱形,理由如下:
过点A作AE⊥BC于E,AF⊥CD于F
因纸条等宽,故AE=AF
又 AB∥CD,AD∥BC
∴四边形ABCD为平行四边形
∵S □ ABCD=BC·AE=CD·AF
∴BC=CD
∴四边形ABCD为菱形例1、把两张等宽的纸条交叉重叠在一起,试探究重叠部分ABCD的形状,并说明理由。
ACDBABCDEF思考:若例1中,已知∠ABC=600,纸条宽为6厘米,试求出重叠部分ABCD的面积。21∵∠AEB=900
∠ABC=600
∴∠BAE=300
∴AB=2BE
设BE=x,则AB=2x
在Rt△AEB中
AE2+BE2=AB2
∴62+x2=(2x)2
∴x=
∴BE=
BC=AB=
∴S菱形ABCD=BC·AE=3、已知:如图,矩形ABCD的对角线AC、BD相交于点O,AP∥BD,DP∥AC,AP、DP相交于点P。求证:四边形AODP是菱形。练 习例2、已知:如图(1), □ ABCD的对角线AC的垂直平分线与边AD,BC分别交于E,F.
求证:四边形AFCE是菱形
AECFBD思考:如图(2),若将例2中的“□ ABCD”改成“矩形ABCD”,其他条件不变,若AB=4厘米,BC=8厘米,求四边形AFCE的面积。(1)(2)O4、如图, 在△ABC中, AB=AC, 点M在边BC上, 过点M分别作AB、AC的平行线, 与AC、AB分别相交于点D、E. 当点M位于BC的什么位置时, 四边形AEMD是菱形?请给予证明.证明:∵EM∥AC,DM∥AB∴四边形AEMD是平行四边形若EM=DM,则□AEMD是菱形∵AB=AC, ∴ ∠B=∠C又∵EM∥AC,DM∥AB∴∠BEM=∠EMD=∠MDC∠B=∠C, ∠BEM=∠CDM, EM=DM在△BME和△CMD中∴ △BME≌ △CDM∴BM=CM∴当M为BC的中点时,四边形AEMD是菱形例2.如图,△ABC中,AB=AC,D为BC的中点,DE⊥AB于E,DF⊥AC于F, EH⊥AC于H, FG⊥AB于G.GF,EH相交于P. 求证:四边形PEDF是菱形。 ABEDCGHFP证明:连接AD∵△ABC中,AB=AC, D为BC的中点∴AD平分∠BAC∵DE⊥AB ,DF⊥AC∴DE=DF∵ DE⊥AB , FG⊥AB∴DE∥FG同理可证∴DF∥EH∴四边形PEDF是平行四边形∴四边形PEDF是菱形。∴∠DEG=∠FGA=90°5、已知:如图,在□ABCD中,AD=2AB,E、F在直线AB上,且AE=AB=BF,求证:CE⊥DF。练 习6、已知:如图,Rt△ABC中,∠ACB=90°,∠BAC=60°,DE垂直平分BC,垂足为D,交AB于E,又点F在DE的延长线上,且AF=CE。求证:四边形ACEF是菱形。练 习7、已知如图,在△ABC,∠ACB=900,AD是角平分线,点E、F分别在AB、AD上,且AE=AC,EF∥BC。
求证:四边形CDEF是菱形O12练 习例3、如图,将一张边长为4的菱形纸片ABCD固定在一个建立了平面直角坐标系的木板上,A,B在x轴上,D在y轴的正半轴上,C在第一象限, ∠BAD=60° 。
(1)求A、B、C、D的坐标;
(2)求过B、C两点的直线的解析式。E课后思考:
如图, □ ABCD中,AB⊥AC,AB=1,BC= ,对角线AC、BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.
(1)证明:当旋转角为90°时,四边形ABEF是平行四边形;
(2)试说明在旋转过程中,线段AF与EC总保留持相等;
(3)在旋转过程中,四边形BEDF可能是菱形吗?如果不能,请说明理由;如果能,试说明理由并求出此时AC绕点O顺时针旋转的度数。ABCDOEF
平分一组对角对称性轴对称图形 ;中心对称图形 注意:菱形的面积等于其对角线乘积的一半菱形判定1.(定义)有一组邻边相等的平行四边形是菱形∵ 在□ ABCD,AB=BC∴ □ ABCD是菱形几何语言:2. 菱形的判定你还有其它的判定方法吗?复习与引入∴ □ ABCD是菱形. (一组邻边相等的平行四边形是菱形)3.对角线互相垂直的平行四边形是菱形.证明:在□ ABCD中又∵AC⊥BD∴BD为AC的中垂线∴AB=ADAO=CO ,BO=DO已知: 在□ ABCD中,对角线AC⊥BD于点O 求证: □ ABCD是菱形(垂直平分线的性质)新 课3、菱形的判定的证明 观察与思考:若四边形ABCD的对角线AC⊥BD,则四边形ABCD是不是菱形?注: 对角线互相垂直的四边形不能判定为菱形。 你能用直尺和圆规作一个菱形吗?请作图并说明理由。思考与探索2.四条边都相等的四边形是菱形证明: ∵ AB=CD,BC=DA∴四边形ABCD为平行四边形又∵AB=BC∴平行四边形ABCD是菱形已知: 在四边形 ABCD中,AB=BC=CD=DA 求证: 四边形ABCD是菱形(两组对边分别相等的四边形为平行四边形)(有一组邻边相等的平行四边形为菱形)新 课3、菱形的判定的证明菱形的判定:一组邻边相等的平行四边形是菱形.对角线互相垂直的平行四边形是菱形.四条边都相等的四边形是菱形.小结:练习1、已知 □ ABCD的对角线AC、BD相交于点O,分别添加下列条件:(1)∠ABC=900 (2)AC ⊥BD (3)AB=BC (4)AC平分∠BAD (5)AO=DO 使得四边形ABCD是菱形的条件的序号有__________
2 、下列条件中,不能判定四边形ABCD为菱形的是( ).
A、AC⊥BD ,AC与BD互相平分
B、AB=BC=CD=DA
C、AB=BC,AD=CD,且AC ⊥BD
D、AB=CD,AD=BC,AC ⊥BD
B(2) (3) (4)C2.下列条件中,不能判定四边形ABCD为菱形的是( ).
A、AC⊥BD ,AC与BD互相平分
B、AB=BC=CD=DA
C、AB=BC,AD=CD,且AC ⊥BD
D、AB=CD,AD=BC,AC ⊥BDB练 习C(4)有一组邻边相等的四边形是菱形; 1、判断下列命题是否正确,并说明理由:(1)对角线互相平分且邻边相等的四边
形是菱形;(2)两组对边分别平行且一组邻边相等
的四边形是菱形;(3)邻角相等的四边形是菱形;练 习XX(8)一条对角线平分一个内角的平行四边形是菱形。 (5)两组对角分别相等且对角线互相垂直的四边形是菱形;(6)对角线互相垂直的四边形是菱形;(7)对角线互相垂直平分的四边形是菱形;练 习X判断下列说法是否正确:1.有一条对角线平分一组对角的四边形是菱形3.对角线相等且互相平分的四边形是菱形矩形2.对角线互相垂直,且一条对角线平分一组对角的四边形是菱形4.对角线互相垂直平分的四边形是菱形邻边相等对角线互相垂直AD=DC AC⊥BD 四边相等AD=DC=CB=BA对角线互相垂直平分AC⊥BD,AO=CO,BO=DO归 纳
例2:如图,已知AD平分∠BAC,DE//AC,DF//AB,AE=5.
(1)判断四边形AEDF的形状?
(2)四边形AEDF的周长为多少?
例1.已知:平行四边形ABCD的对角线AC的垂直平分线与边AD,BC分别交于E,F。 求证:四边形AFCE是菱形。ABEDCFO12证明:平行四边形ABCD中AD∥BC∴∠1=∠2,∠3=∠443EF垂直平分AC∴AO=CO,AF=CF,AE=CE∴ △AOF≌△COE∴ AF=CE∴ AF=CF=AE=CE∴四边形AFCE是菱形四条边都相等的四边形是菱形例1.已知:平行四边形ABCD的对角线AC的垂直平分线与边AD,BC分别交于E,F。 求证:四边形AFCE是菱形。ABEDCFO12证明:平行四边形ABCD中AD∥BC∴∠1=∠2,∠3=∠443EF垂直平分AC∴AO=CO,AF=CF,∴ △AOF≌△COE∴ AF=CE∴平行四边形四边形AFCE是菱形又AF∥CE∴四边形AFCE是平行四边形一组邻边相等的平行四边形是菱形例1.已知:平行四边形ABCD的对角线AC的垂直平分线与边AD,BC分别交于E,F。 求证:四边形AFCE是菱形。ABEDCFO123’证明:平行四边形ABCD中AD∥BC∴∠1=∠2,∠3=∠443EF垂直平分AC∴AO=CO,AC⊥EF,∴ △AOF≌△COE∴ AF=CE∴平行四边形四边形AFCE是菱形又AF∥CE∴四边形AFCE是平行四边形对角线互相垂直的平行四边形是菱形例3.如图,已知AD是△ABC的角平分线,
DE∥AC交AB于E,DF∥AB交AC于F,
求证:AD⊥EF。
1 2
3
证明:∵DE∥AC ,DF∥AB∴四边形AEDF是平行四边形∴ ∠2=∠3∵ AD是△ABC的角平分线∴ ∠1=∠2∴ ∠1=∠3∴ AE=DE∴ □AEDF是菱形∴ AD⊥EF∵DE∥AC 例1、把两张等宽的纸条交叉重叠在一起,试探究重叠部分ABCD的形状,并说明理由。
ACDBABCDEF12解:重叠部分为菱形,理由如下:
过点A作AE⊥BC于E,AF⊥CD于F
因纸条等宽,故AE=AF
又 AB∥CD,AD∥BC
∴四边形ABCD为平行四边形
∵S □ ABCD=BC·AE=CD·AF
∴BC=CD
∴四边形ABCD为菱形例1、把两张等宽的纸条交叉重叠在一起,试探究重叠部分ABCD的形状,并说明理由。
ACDBABCDEF思考:若例1中,已知∠ABC=600,纸条宽为6厘米,试求出重叠部分ABCD的面积。21∵∠AEB=900
∠ABC=600
∴∠BAE=300
∴AB=2BE
设BE=x,则AB=2x
在Rt△AEB中
AE2+BE2=AB2
∴62+x2=(2x)2
∴x=
∴BE=
BC=AB=
∴S菱形ABCD=BC·AE=3、已知:如图,矩形ABCD的对角线AC、BD相交于点O,AP∥BD,DP∥AC,AP、DP相交于点P。求证:四边形AODP是菱形。练 习例2、已知:如图(1), □ ABCD的对角线AC的垂直平分线与边AD,BC分别交于E,F.
求证:四边形AFCE是菱形
AECFBD思考:如图(2),若将例2中的“□ ABCD”改成“矩形ABCD”,其他条件不变,若AB=4厘米,BC=8厘米,求四边形AFCE的面积。(1)(2)O4、如图, 在△ABC中, AB=AC, 点M在边BC上, 过点M分别作AB、AC的平行线, 与AC、AB分别相交于点D、E. 当点M位于BC的什么位置时, 四边形AEMD是菱形?请给予证明.证明:∵EM∥AC,DM∥AB∴四边形AEMD是平行四边形若EM=DM,则□AEMD是菱形∵AB=AC, ∴ ∠B=∠C又∵EM∥AC,DM∥AB∴∠BEM=∠EMD=∠MDC∠B=∠C, ∠BEM=∠CDM, EM=DM在△BME和△CMD中∴ △BME≌ △CDM∴BM=CM∴当M为BC的中点时,四边形AEMD是菱形例2.如图,△ABC中,AB=AC,D为BC的中点,DE⊥AB于E,DF⊥AC于F, EH⊥AC于H, FG⊥AB于G.GF,EH相交于P. 求证:四边形PEDF是菱形。 ABEDCGHFP证明:连接AD∵△ABC中,AB=AC, D为BC的中点∴AD平分∠BAC∵DE⊥AB ,DF⊥AC∴DE=DF∵ DE⊥AB , FG⊥AB∴DE∥FG同理可证∴DF∥EH∴四边形PEDF是平行四边形∴四边形PEDF是菱形。∴∠DEG=∠FGA=90°5、已知:如图,在□ABCD中,AD=2AB,E、F在直线AB上,且AE=AB=BF,求证:CE⊥DF。练 习6、已知:如图,Rt△ABC中,∠ACB=90°,∠BAC=60°,DE垂直平分BC,垂足为D,交AB于E,又点F在DE的延长线上,且AF=CE。求证:四边形ACEF是菱形。练 习7、已知如图,在△ABC,∠ACB=900,AD是角平分线,点E、F分别在AB、AD上,且AE=AC,EF∥BC。
求证:四边形CDEF是菱形O12练 习例3、如图,将一张边长为4的菱形纸片ABCD固定在一个建立了平面直角坐标系的木板上,A,B在x轴上,D在y轴的正半轴上,C在第一象限, ∠BAD=60° 。
(1)求A、B、C、D的坐标;
(2)求过B、C两点的直线的解析式。E课后思考:
如图, □ ABCD中,AB⊥AC,AB=1,BC= ,对角线AC、BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.
(1)证明:当旋转角为90°时,四边形ABEF是平行四边形;
(2)试说明在旋转过程中,线段AF与EC总保留持相等;
(3)在旋转过程中,四边形BEDF可能是菱形吗?如果不能,请说明理由;如果能,试说明理由并求出此时AC绕点O顺时针旋转的度数。ABCDOEF
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
