2021-2022学年华东师大版八年级数学上学期《第14章勾股定理》期末综合复习训练(word版含答案)
文档属性
| 名称 | 2021-2022学年华东师大版八年级数学上学期《第14章勾股定理》期末综合复习训练(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 290.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-02 16:53:51 | ||
图片预览




文档简介
2021-2022学年华师大版八年级数学上册《第14章勾股定理》期末综合复习训练(附答案)
1.已知Rt△ABC的两直角边分别是6cm,8cm,则Rt△ABC的斜边上的高是( )
A.4.8cm B.2.4cm C.48cm D.10cm
2.在周长为24的直角三角形中,斜边长为11,则该三角形的面积为( )
A.6 B.12 C.24 D.48
3.已知直角三角形纸片的两条直角边分别为m和n(m<n),过此三角形锐角的顶点把该纸片剪成两个三角形,若这两个三角形都为等腰三角形,则有( )
A.m2+2mn+n2=0 B.m2﹣2mn+n2=0
C.m2+2mn﹣n2=0 D.m2﹣2mn﹣n2=0
4.《九章算术》中的“折竹抵地”问题:今有竹高二丈,末折抵地,去根九尺,问折高者几何?意思是一根竹子,原高两丈(一丈=10尺),一阵风将竹子折断,其竹稍恰好抵地,抵地处离竹子底部9尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为( )
A.x2﹣9=(20﹣x)2 B.x2﹣92=(20﹣x)2
C.x2+9=(20﹣x)2 D.x2+92=(20﹣x)2
5.如图,∠AOB=60°,C是BO延长线上一点,OC=12cm,动点P从点C出发沿CB以2cm/s的速度移动,动点Q从点O出发沿OA以1cm/s的速度移动,如果点P,Q同时出发,用t表示移动的时间,若△POQ是等腰三角形,此时t的值是( )
A.6或12 B.4或12 C.4或6 D.6或8
6.《九章算术》提供了许多整勾股数,如(3,4,5),(5,12,13),(7,24,25)等,并把一组勾股数中最大的数称为“弦数”.后人在此基础上进一步研究,得到如下规律:若m是大于1的奇数,把它平方后拆成相邻的两个整数,那么m与这两个整数构成组勾股数;若m是大于2的偶数,把它除以2后再平方,然后把这个平方数分别减1,加1得到两个整数,那么m与这两个整数构成一组勾股数.由上述方法得到的勾股数称为“由m生成的勾股数”.根据以上规律,“由8生成的勾股数”的“弦数”为( )
A.16 B.17 C.25 D.64
7.如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形.如果AB=10,AH=6,那么EF等于( )
A.8 B.6 C.4 D.2
8.已知△ABC的三边分别为a,b,c,下列条件无法判定△ABC是直角三角形的是( )
A.a2+b2=c2 B.a:b:c=2:2:3
C.∠A:∠B:∠C=5:2:3 D.∠A=∠C﹣∠B
9.如图所示,是一块由花园小道围成的边长为12米的正方形绿地,在离C处5米的绿地旁边B处有健身器材,为提醒居住在A处的居民爱护绿地,不直接穿过绿地从A到B,而是沿小道从A→C→B.小丽想在A处树立一个标牌“沿路多走■米,共建美丽家园”请问:小丽在标牌■填上的数字是 .
10.如图,甲、乙两艘客轮同时离开港口C,各自沿一固定方向航行,甲客轮每小时航行16nmile,乙客轮每小时航行12nmile,它们离开港口一个半小时后分别位于点A、B处,且相距30nmile.如果知道甲客轮沿着北偏西45°方向航行,则乙客轮的航行方向可能是 .
11.如图,在正方形形成的网格上点A、B、C都在网格线交点上,则∠ACB= °.
12.如图, ABCD中,∠BCD和∠ABC的平分线分别交AD于E.F两点,CE、BF交于点G,若AB=3,BC=4,则EG2+FG2= .
13.如图,在△ABC中,已知:∠ACB=90°,AB=10cm,AC=6cm,动点P从点B出发,沿射线BC以1cm/s的速度运动,设运动的时间为t秒,连接PA,当△ABP为等腰三角形时,t的值为 .
14.如图是马口生态公园的一角,有人为了抄近道而避开横平竖直的路的拐角∠ABC,而走“捷径AC”,于是在草坪内走出了一条不该有的“路AC”.已知AB=40米,BC=30米,他们踩坏草坪,只为少走 米的路.
15.一艘轮船和一艘渔船同时沿各自的航向从港口O出发,如图所示,轮船从港口O沿北偏西20°的方向航行60海里到达点A处,同一时刻渔船已航行到与港口O相距80海里的点B处,若A、B两点相距100海里,则渔船在港口南偏西 °的方向.
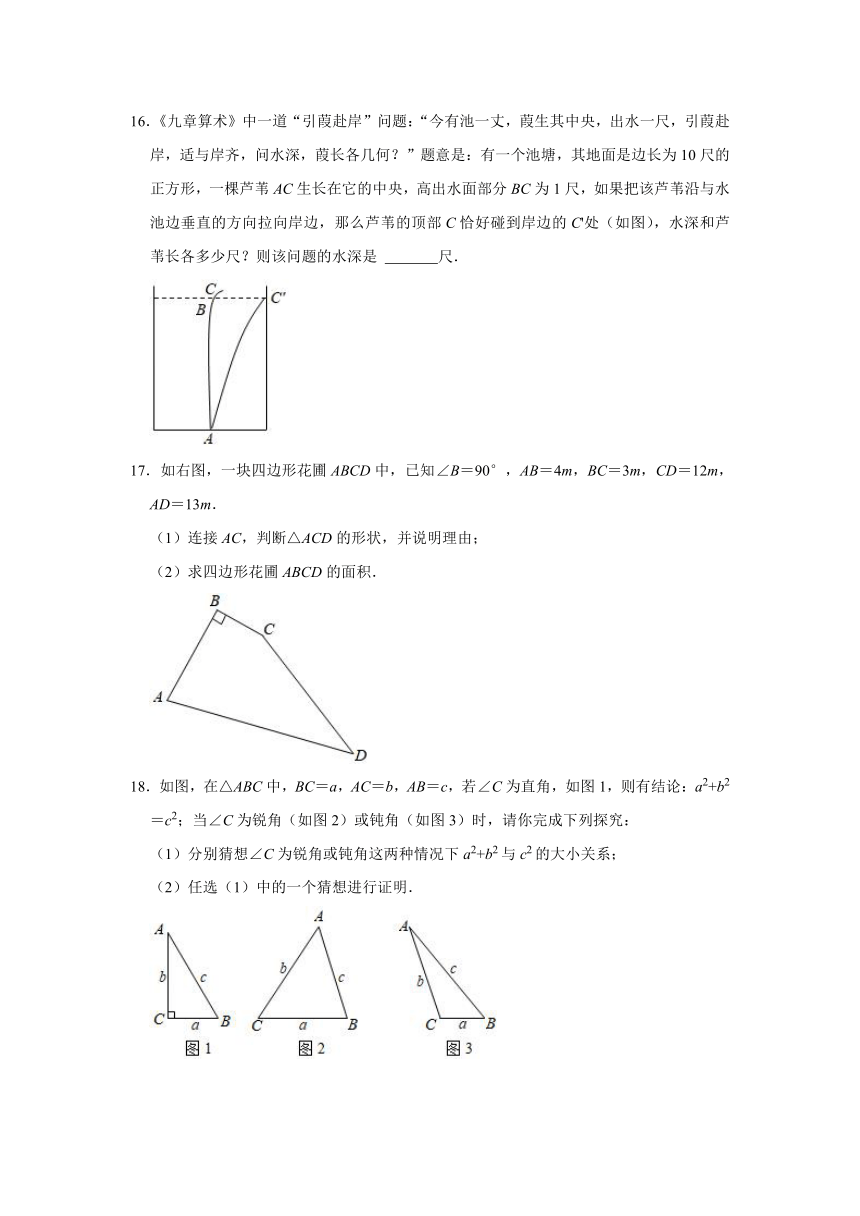
16.《九章算术》中一道“引葭赴岸”问题:“今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深,葭长各几何?”题意是:有一个池塘,其地面是边长为10尺的正方形,一棵芦苇AC生长在它的中央,高出水面部分BC为1尺,如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部C恰好碰到岸边的C'处(如图),水深和芦苇长各多少尺?则该问题的水深是 尺.
17.如右图,一块四边形花圃ABCD中,已知∠B=90°,AB=4m,BC=3m,CD=12m,AD=13m.
(1)连接AC,判断△ACD的形状,并说明理由;
(2)求四边形花圃ABCD的面积.
18.如图,在△ABC中,BC=a,AC=b,AB=c,若∠C为直角,如图1,则有结论:a2+b2=c2;当∠C为锐角(如图2)或钝角(如图3)时,请你完成下列探究:
(1)分别猜想∠C为锐角或钝角这两种情况下a2+b2与c2的大小关系;
(2)任选(1)中的一个猜想进行证明.
19.如图,某港口P位于东西方向的海岸线上.“综合执法1号”、“综合执法2号”轮船同时离开港口,各自沿一定方向执法巡逻,“综合执法1号”每小时航行16nmile,“综合执法2号”每小时航行12nmile,它们离开港口一个半小时后分别位于点Q,R处,且相距30nmile.
(1)求PQ,PR的长度;
(2)如果知道“综合执法1号”沿北偏东61°方向航行,能知道“综合执法2号”沿哪个方向航行吗?
20.为了积极宣传防疫知识,某地政府采用了移动车进行广播.如图,小明家在一条笔直的公路MN的一侧点A处,且到公路MN的距离AB为600m.若广播车周围1000m以内都能听到广播宣传,则当广播车以250m/min的速度在公路MN上沿MN方向行驶时,在小明家是否能听到广播宣传?若能,请求出在小明家共能听到多长时间的广播宣传.
21.如图,某港口O位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.
(1)若它们离开港口一个半小时后分别位于A、B处,且相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?说明理由.
(2)若“远航”号沿北偏东60°方向航行,经过两个小时后位于F处,此时船上有一名乘客需要紧急回到PE海岸线上,若他从F处出发,乘坐的快艇的速度是每小时80海里.他能在半小时内回到海岸线吗?说明理由.
22.勾股定理神奇而美妙,它的证法多种多样,在学习了教材中介绍的拼图证法以后,小华突发灵感,给出了如图拼图:
两个全等的直角三角板ABC和直角三角板DEF,顶点F在BC边上,顶点C、D重合,连接AE、EB.设AB、DE交于点G.∠ACB=∠DFE=90°,BC=EF=a,AC=DF=b(a>b),AB=DE=c.请你回答以下问题:
(1)填空:∠AGE= °,S四边形ADBE= c2.
(2)请用两种方法计算四边形ACBE的面积,并以此为基础证明勾股定理.
23.在△ABC中,
(1)如图1,AC=15,AD=9,CD=12,BC=20,求△ABC的面积;
(2)如图2,AC=13,BC=20,AB=11,求△ABC的面积.
参考答案
1.解:设Rt△ABC斜边上的高为hcm,
∵Rt△ABC的两直角边分别是6cm,8cm,
∴斜边长==10(cm),
∵×10×h=×6×8,
∴h=4.8(cm),
即Rt△ABC的斜边上的高是4.8cm,
故选:A.
2.解:设直角三角形的一直角边长为x,另一直角边为y,
由题意可得:x+y=24﹣11=13,
∴(x+y)2=132①,
由勾股定理可得:x2+y2=112②,
①﹣②得:2xy=48,
∴xy=24,
∴该三角形的面积为:xy=×24=12,
故选:B.
3.解:如图,
m2+m2=(n﹣m)2,
2m2=n2﹣2mn+m2,
m2+2mn﹣n2=0.
故选:C.
4.解:如图,设折断处离地面的高度为x尺,则AB=(20﹣x)尺,BC=9尺,
在Rt△ABC中,AC2+BC2=AB2,即x2+92=(20﹣x)2.
故选:D.
5.解:分两种情况:(1)当点P在线段OC上时,
设t时后△POQ是等腰三角形,
有OP=OC﹣CP=OQ,
即12﹣2t=t,
解得,t=4;
(2)当点P在CO的延长线上时,此时经过CO时的时间已用6s,
当△POQ是等腰三角形时,∵∠POQ=60°,
∴△POQ是等边三角形,
∴OP=OQ,
即2(t﹣6)=t,
解得,t=12,
故选:B.
6.解:∵由8生成的勾股数”的“弦数”记为A,
∴()2=16,16﹣1=15,16+1=17,
故A=17,
故选:B.
7.解:∵△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,
∴AH=DE=6,AD=AB=10,
在Rt△ADE中,
AE===8,
∴HE=AE﹣AH=8﹣6=2,
∵四边形EFGH是正方形,
∴EF=HE=2,
故选:D.
8.解:设△ABC中,∠A的对边是a,∠B的对边是b,∠C的对边是c,
A.∵a2+b2=c2,
∴∠C=90°,
∴△ABC是直角三角形,故本选项不符合题意;
B.∵a:b:c=2:2:3,
∴a2+b2≠c2,
∴最大角∠C≠90°,
∴△ABC不是直角三角形,故本选项符合题意;
C.∵∠A:∠B:∠C=5:2:3,∠A+∠B+∠C=180°,
∴∠A=×180°=90°,
∴△ABC是直角三角形,故本选项不符合题意;
D.∵∠A=∠C﹣∠B,
∴∠A+∠B=∠C,
∵∠A+∠B+∠C=180°,
∴2∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形,故本选项不符合题意;
故选:B.
9.解:在Rt△ABC中,AB为斜边,
∴==13米,
少走的距离为
AC+BC﹣AB=(12+5)﹣13(米)=4米
答:小明在标牌■填上的数字是4.
故答案为:4.
10.解:AC的长度为:16×1.5=24(n mile),
BC的长度为:12×1.5=18(n mile),
∵302=242+182,
∴AB2=AC2+BC2,
∴△ABC是直角三角形,∠ACB=90°,
∵甲客轮沿着北偏西45°方向航行,
∴乙客轮的航行方向可能是北偏东45°,
故答案为:北偏东45°.
11.解:连接AB,如图所示:
由勾股定理得:AB=BC=,BC=,
∴AB2+BC2=AC2,
∴△ABC是直角三角形,
∵AB=BC,
∴△ABC是等腰直角三角形,
∴∠ACB=45°,
故答案为:45.
12.解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,AB=CD,
∴∠ABC+∠DCE=180°,∠AFB=∠CBF,∠DEC=∠BCE,∠ABC+∠DCE=180°,
∵∠BCD和∠ABC的平分线分别交AD于E,F两点,
∴∠ABF=∠CBF=∠ABC,∠BCE=∠DCE=∠BCD,
∴∠ABF=∠AFB,∠DCE=∠DEC,∠CBF+∠BCE=(∠ABC+BCD)=90°,
∴AF=AB,DE=CD,∠BGC=90°,
∴AF=DE,
∵四边形ABCD是平行四边形,
∴AD=BC=4,AF=DE=AB=3,
∴EF=AF+DE﹣AD=2,
∵∠EGF=∠BGC=90°,
∴EG2+FG2=EF2=4.
故答案为:4.
13.解:在△ABC中,∠ACB=90°,
由勾股定理得:BC=cm,
∵△ABP为等腰三角形,
当AB=AP时,则BP=2BC=16cm,即t=16;
当BA=BP=10cm时,则t=10;
当PA=PB时,如图:设BP=PA=x,则PC=8﹣x,
在Rt△ACP中,由勾股定理得:
PC2+AC2=AP2,
∴(8﹣x)2+62=x2,
解得x=,
∴t=.
综上所述:t的值为16或10或.
故答案为:16或10或.
14.解:在Rt△ABC中,∵AB=40米,BC=30米,
∴AC==50,30+40﹣50=20,
∴他们踩坏了50米的草坪,只为少走20米的路.
故答案为:20.
15.解:∵OA=60海里,OB=80海里,AB=100海里,
∴OA2+OB2=AB2,
∴∠AOB=90°
∵∠NOA=20°,
∴∠BOS=180°﹣20°﹣90°=70°,
故渔船在港口南偏西70°的方向,
故答案为:70.
16.解:依题意画出图形,
设芦苇长AC=AC′=x尺,
则水深AB=(x﹣1)尺,
∵C′E=10尺,
∴C′B=5尺,
在Rt△AC′B中,
52+(x﹣1)2=x2,
解得x=13,
即芦苇长13尺,水深为12尺,
故答案为:12.
17.解:(1)连接AC,
因为∠B=90°,所以直角△ABC中,由勾股定理得:
AC2=AB2+BC2,
AC2=42+32,
AC2=25,
∴AC=5m,又CD=12m,AD=13m,
所以△ACD中,AC2+CD2=AD2,
所以△ACD是直角三角形;
(2)S四边形ABCD=AC CD+AB BC
S四边形ABCD=×5×12+×4×3
=30+6
=36(m2),
答:该花圃的面积为36m2.
18.解:(1)猜想:若∠C为锐角时,a2+b2>c2,若∠C为钝角时,a2+b2<c2;
(2)当∠C为锐角时,a2+b2>c2,证明如下:
如图,过点A作AD⊥CB于点D,设CD=x,则BD=a﹣x,
在直角三角形ACD中,AD2=b2﹣x2,
在直角三角形ABD中,AD2=c2﹣(a﹣x)2,
∴b2﹣x2=c2﹣(a﹣x)2,即a2+b2=c2+2ax,
∵a>0,x>0,
∴a2+b2>c2,
当∠C为钝角时,a2+b2<c2,证明如下:
如图,过点A作BC的垂线交BC的延长线于点M,CM=y,则BM=a+y,
在直角三角形ACM中,AM2=b2﹣y2,
在直角三角形ABM中,AM2=c2﹣(a+y)2,
∴b2﹣y2=c2﹣(a+y)2,即a2+b2=c2﹣2ay,
∵a>0,y>0,
∴a2+b2<c2.
19.解:(1)由题意可得:RP=12×1.5=18(海里),PQ=16×1.5=24(海里);
(2)能,
理由:∵RP=12×1.5=18海里,PQ=16×1.5=24海里,QR=30海里,
∵182+242=302,
∴△RPQ是直角三角形,
∴∠RPQ=90°,
∵“综合执法1号”沿北偏东61°方向航行,
∴∠QPS=61°,
∴∠SPR=90°﹣61°=29°,
∴“综合执法2号”沿北偏西29°方向航行方向航行.
20.解:小明能听到宣传,
理由:∵村庄A到公路MN的距离为600米<1000米,
∴小明能听到宣传;
如图:假设当宣讲车行驶到P点开始小明听到广播,行驶到Q点小明听不到广播,
则AP=AQ=1000米,AB=600米,
∴BP=BQ==800(米),
∴PQ=1600米,
∴小明听到广播的时间为:1600÷250=6.4(分钟),
∴他总共能听到6.4分钟的广播.
21.解:(1)∵OA=16×1.5=24,OB=12×1.5=18,AB=30,
∴OA2+OB2=AB2,
∴△AOB是直角三角形,
∴∠AOB=90°,
∵“远航”号沿东北方向航行,
∴∠AON=45°,
∴∠BON=90°﹣45°=45°,
∴“海天”号沿西北方向航行;
(2)过点F作FD⊥PE于D,
OF=16×2=32,
∵∠NOF=60°,
∴∠FOD=90°﹣60°=30°,
∴FD=,
∴16÷80=0.2(小时),
∵0.2<0.5,
∴能在半小时内回到海岸线.
22.解:(1)∵△ABC≌△DEF,
∴∠EDF=∠CAB,
∵∠EDF+∠CAE=90°,
∴∠ACE+∠CAB=90°,
∴∠AGC=90°,
∴∠AGE=180°﹣∠AGC=90°;
∴DE⊥AB,
∴S四边形ADBE=S△ACB+S△ABE=AB DG+AB EG=AB (DG+EG)=AB DE=c2,
故答案为:90,;
(2)∵四边形ACBE的面积=S△ACB+S△ABE=AB DG+AB EG=AB (DG+EG)=AB DE=c2,
四边形ACBE的面积=S四边形ACFE+S△EFB=×(AC+EF) CF+BF EF=(b+a)b+(a﹣b) a=b2+ab+a2﹣ab=a2+b2,
∴c2=a2+b2,
即a2+b2=c2.
23.解:(1)∵CD2+AD2=144+81=225,AC2=225,
∴CD2+AD2=CA2,
∴△△ADC是直角三角形,
∴∠ADC=90°,
∴CD⊥AB,
∴∠ADC=90°,
∴BD==16,
∴AB=AD+DB=16+9=25,
∴△ABC的面积=×25×12=150;
(2)过C作CD⊥BA的延长线于点D,
∵CD⊥AB,
∴∠CDB=90°,
设AD为x,DB=(x+11),由勾股定理得:CD2=AC2﹣AD2,CD2=BC2﹣DB2,
即AC2﹣AD2=BC2﹣DB2,
则132﹣x2=202﹣(x+11)2,
解得:x=5,
∴CD===12,
∴△ABC的面积= AB CD=×11×12=66.
1.已知Rt△ABC的两直角边分别是6cm,8cm,则Rt△ABC的斜边上的高是( )
A.4.8cm B.2.4cm C.48cm D.10cm
2.在周长为24的直角三角形中,斜边长为11,则该三角形的面积为( )
A.6 B.12 C.24 D.48
3.已知直角三角形纸片的两条直角边分别为m和n(m<n),过此三角形锐角的顶点把该纸片剪成两个三角形,若这两个三角形都为等腰三角形,则有( )
A.m2+2mn+n2=0 B.m2﹣2mn+n2=0
C.m2+2mn﹣n2=0 D.m2﹣2mn﹣n2=0
4.《九章算术》中的“折竹抵地”问题:今有竹高二丈,末折抵地,去根九尺,问折高者几何?意思是一根竹子,原高两丈(一丈=10尺),一阵风将竹子折断,其竹稍恰好抵地,抵地处离竹子底部9尺远,问折断处离地面的高度是多少?设折断处离地面的高度为x尺,则可列方程为( )
A.x2﹣9=(20﹣x)2 B.x2﹣92=(20﹣x)2
C.x2+9=(20﹣x)2 D.x2+92=(20﹣x)2
5.如图,∠AOB=60°,C是BO延长线上一点,OC=12cm,动点P从点C出发沿CB以2cm/s的速度移动,动点Q从点O出发沿OA以1cm/s的速度移动,如果点P,Q同时出发,用t表示移动的时间,若△POQ是等腰三角形,此时t的值是( )
A.6或12 B.4或12 C.4或6 D.6或8
6.《九章算术》提供了许多整勾股数,如(3,4,5),(5,12,13),(7,24,25)等,并把一组勾股数中最大的数称为“弦数”.后人在此基础上进一步研究,得到如下规律:若m是大于1的奇数,把它平方后拆成相邻的两个整数,那么m与这两个整数构成组勾股数;若m是大于2的偶数,把它除以2后再平方,然后把这个平方数分别减1,加1得到两个整数,那么m与这两个整数构成一组勾股数.由上述方法得到的勾股数称为“由m生成的勾股数”.根据以上规律,“由8生成的勾股数”的“弦数”为( )
A.16 B.17 C.25 D.64
7.如图是“赵爽弦图”,△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,四边形ABCD和EFGH都是正方形.如果AB=10,AH=6,那么EF等于( )
A.8 B.6 C.4 D.2
8.已知△ABC的三边分别为a,b,c,下列条件无法判定△ABC是直角三角形的是( )
A.a2+b2=c2 B.a:b:c=2:2:3
C.∠A:∠B:∠C=5:2:3 D.∠A=∠C﹣∠B
9.如图所示,是一块由花园小道围成的边长为12米的正方形绿地,在离C处5米的绿地旁边B处有健身器材,为提醒居住在A处的居民爱护绿地,不直接穿过绿地从A到B,而是沿小道从A→C→B.小丽想在A处树立一个标牌“沿路多走■米,共建美丽家园”请问:小丽在标牌■填上的数字是 .
10.如图,甲、乙两艘客轮同时离开港口C,各自沿一固定方向航行,甲客轮每小时航行16nmile,乙客轮每小时航行12nmile,它们离开港口一个半小时后分别位于点A、B处,且相距30nmile.如果知道甲客轮沿着北偏西45°方向航行,则乙客轮的航行方向可能是 .
11.如图,在正方形形成的网格上点A、B、C都在网格线交点上,则∠ACB= °.
12.如图, ABCD中,∠BCD和∠ABC的平分线分别交AD于E.F两点,CE、BF交于点G,若AB=3,BC=4,则EG2+FG2= .
13.如图,在△ABC中,已知:∠ACB=90°,AB=10cm,AC=6cm,动点P从点B出发,沿射线BC以1cm/s的速度运动,设运动的时间为t秒,连接PA,当△ABP为等腰三角形时,t的值为 .
14.如图是马口生态公园的一角,有人为了抄近道而避开横平竖直的路的拐角∠ABC,而走“捷径AC”,于是在草坪内走出了一条不该有的“路AC”.已知AB=40米,BC=30米,他们踩坏草坪,只为少走 米的路.
15.一艘轮船和一艘渔船同时沿各自的航向从港口O出发,如图所示,轮船从港口O沿北偏西20°的方向航行60海里到达点A处,同一时刻渔船已航行到与港口O相距80海里的点B处,若A、B两点相距100海里,则渔船在港口南偏西 °的方向.
16.《九章算术》中一道“引葭赴岸”问题:“今有池一丈,葭生其中央,出水一尺,引葭赴岸,适与岸齐,问水深,葭长各几何?”题意是:有一个池塘,其地面是边长为10尺的正方形,一棵芦苇AC生长在它的中央,高出水面部分BC为1尺,如果把该芦苇沿与水池边垂直的方向拉向岸边,那么芦苇的顶部C恰好碰到岸边的C'处(如图),水深和芦苇长各多少尺?则该问题的水深是 尺.
17.如右图,一块四边形花圃ABCD中,已知∠B=90°,AB=4m,BC=3m,CD=12m,AD=13m.
(1)连接AC,判断△ACD的形状,并说明理由;
(2)求四边形花圃ABCD的面积.
18.如图,在△ABC中,BC=a,AC=b,AB=c,若∠C为直角,如图1,则有结论:a2+b2=c2;当∠C为锐角(如图2)或钝角(如图3)时,请你完成下列探究:
(1)分别猜想∠C为锐角或钝角这两种情况下a2+b2与c2的大小关系;
(2)任选(1)中的一个猜想进行证明.
19.如图,某港口P位于东西方向的海岸线上.“综合执法1号”、“综合执法2号”轮船同时离开港口,各自沿一定方向执法巡逻,“综合执法1号”每小时航行16nmile,“综合执法2号”每小时航行12nmile,它们离开港口一个半小时后分别位于点Q,R处,且相距30nmile.
(1)求PQ,PR的长度;
(2)如果知道“综合执法1号”沿北偏东61°方向航行,能知道“综合执法2号”沿哪个方向航行吗?
20.为了积极宣传防疫知识,某地政府采用了移动车进行广播.如图,小明家在一条笔直的公路MN的一侧点A处,且到公路MN的距离AB为600m.若广播车周围1000m以内都能听到广播宣传,则当广播车以250m/min的速度在公路MN上沿MN方向行驶时,在小明家是否能听到广播宣传?若能,请求出在小明家共能听到多长时间的广播宣传.
21.如图,某港口O位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16海里,“海天”号每小时航行12海里.
(1)若它们离开港口一个半小时后分别位于A、B处,且相距30海里.如果知道“远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?说明理由.
(2)若“远航”号沿北偏东60°方向航行,经过两个小时后位于F处,此时船上有一名乘客需要紧急回到PE海岸线上,若他从F处出发,乘坐的快艇的速度是每小时80海里.他能在半小时内回到海岸线吗?说明理由.
22.勾股定理神奇而美妙,它的证法多种多样,在学习了教材中介绍的拼图证法以后,小华突发灵感,给出了如图拼图:
两个全等的直角三角板ABC和直角三角板DEF,顶点F在BC边上,顶点C、D重合,连接AE、EB.设AB、DE交于点G.∠ACB=∠DFE=90°,BC=EF=a,AC=DF=b(a>b),AB=DE=c.请你回答以下问题:
(1)填空:∠AGE= °,S四边形ADBE= c2.
(2)请用两种方法计算四边形ACBE的面积,并以此为基础证明勾股定理.
23.在△ABC中,
(1)如图1,AC=15,AD=9,CD=12,BC=20,求△ABC的面积;
(2)如图2,AC=13,BC=20,AB=11,求△ABC的面积.
参考答案
1.解:设Rt△ABC斜边上的高为hcm,
∵Rt△ABC的两直角边分别是6cm,8cm,
∴斜边长==10(cm),
∵×10×h=×6×8,
∴h=4.8(cm),
即Rt△ABC的斜边上的高是4.8cm,
故选:A.
2.解:设直角三角形的一直角边长为x,另一直角边为y,
由题意可得:x+y=24﹣11=13,
∴(x+y)2=132①,
由勾股定理可得:x2+y2=112②,
①﹣②得:2xy=48,
∴xy=24,
∴该三角形的面积为:xy=×24=12,
故选:B.
3.解:如图,
m2+m2=(n﹣m)2,
2m2=n2﹣2mn+m2,
m2+2mn﹣n2=0.
故选:C.
4.解:如图,设折断处离地面的高度为x尺,则AB=(20﹣x)尺,BC=9尺,
在Rt△ABC中,AC2+BC2=AB2,即x2+92=(20﹣x)2.
故选:D.
5.解:分两种情况:(1)当点P在线段OC上时,
设t时后△POQ是等腰三角形,
有OP=OC﹣CP=OQ,
即12﹣2t=t,
解得,t=4;
(2)当点P在CO的延长线上时,此时经过CO时的时间已用6s,
当△POQ是等腰三角形时,∵∠POQ=60°,
∴△POQ是等边三角形,
∴OP=OQ,
即2(t﹣6)=t,
解得,t=12,
故选:B.
6.解:∵由8生成的勾股数”的“弦数”记为A,
∴()2=16,16﹣1=15,16+1=17,
故A=17,
故选:B.
7.解:∵△ABH、△BCG、△CDF和△DAE是四个全等的直角三角形,
∴AH=DE=6,AD=AB=10,
在Rt△ADE中,
AE===8,
∴HE=AE﹣AH=8﹣6=2,
∵四边形EFGH是正方形,
∴EF=HE=2,
故选:D.
8.解:设△ABC中,∠A的对边是a,∠B的对边是b,∠C的对边是c,
A.∵a2+b2=c2,
∴∠C=90°,
∴△ABC是直角三角形,故本选项不符合题意;
B.∵a:b:c=2:2:3,
∴a2+b2≠c2,
∴最大角∠C≠90°,
∴△ABC不是直角三角形,故本选项符合题意;
C.∵∠A:∠B:∠C=5:2:3,∠A+∠B+∠C=180°,
∴∠A=×180°=90°,
∴△ABC是直角三角形,故本选项不符合题意;
D.∵∠A=∠C﹣∠B,
∴∠A+∠B=∠C,
∵∠A+∠B+∠C=180°,
∴2∠C=180°,
∴∠C=90°,
∴△ABC是直角三角形,故本选项不符合题意;
故选:B.
9.解:在Rt△ABC中,AB为斜边,
∴==13米,
少走的距离为
AC+BC﹣AB=(12+5)﹣13(米)=4米
答:小明在标牌■填上的数字是4.
故答案为:4.
10.解:AC的长度为:16×1.5=24(n mile),
BC的长度为:12×1.5=18(n mile),
∵302=242+182,
∴AB2=AC2+BC2,
∴△ABC是直角三角形,∠ACB=90°,
∵甲客轮沿着北偏西45°方向航行,
∴乙客轮的航行方向可能是北偏东45°,
故答案为:北偏东45°.
11.解:连接AB,如图所示:
由勾股定理得:AB=BC=,BC=,
∴AB2+BC2=AC2,
∴△ABC是直角三角形,
∵AB=BC,
∴△ABC是等腰直角三角形,
∴∠ACB=45°,
故答案为:45.
12.解:∵四边形ABCD是平行四边形,
∴AB∥CD,AD∥BC,AB=CD,
∴∠ABC+∠DCE=180°,∠AFB=∠CBF,∠DEC=∠BCE,∠ABC+∠DCE=180°,
∵∠BCD和∠ABC的平分线分别交AD于E,F两点,
∴∠ABF=∠CBF=∠ABC,∠BCE=∠DCE=∠BCD,
∴∠ABF=∠AFB,∠DCE=∠DEC,∠CBF+∠BCE=(∠ABC+BCD)=90°,
∴AF=AB,DE=CD,∠BGC=90°,
∴AF=DE,
∵四边形ABCD是平行四边形,
∴AD=BC=4,AF=DE=AB=3,
∴EF=AF+DE﹣AD=2,
∵∠EGF=∠BGC=90°,
∴EG2+FG2=EF2=4.
故答案为:4.
13.解:在△ABC中,∠ACB=90°,
由勾股定理得:BC=cm,
∵△ABP为等腰三角形,
当AB=AP时,则BP=2BC=16cm,即t=16;
当BA=BP=10cm时,则t=10;
当PA=PB时,如图:设BP=PA=x,则PC=8﹣x,
在Rt△ACP中,由勾股定理得:
PC2+AC2=AP2,
∴(8﹣x)2+62=x2,
解得x=,
∴t=.
综上所述:t的值为16或10或.
故答案为:16或10或.
14.解:在Rt△ABC中,∵AB=40米,BC=30米,
∴AC==50,30+40﹣50=20,
∴他们踩坏了50米的草坪,只为少走20米的路.
故答案为:20.
15.解:∵OA=60海里,OB=80海里,AB=100海里,
∴OA2+OB2=AB2,
∴∠AOB=90°
∵∠NOA=20°,
∴∠BOS=180°﹣20°﹣90°=70°,
故渔船在港口南偏西70°的方向,
故答案为:70.
16.解:依题意画出图形,
设芦苇长AC=AC′=x尺,
则水深AB=(x﹣1)尺,
∵C′E=10尺,
∴C′B=5尺,
在Rt△AC′B中,
52+(x﹣1)2=x2,
解得x=13,
即芦苇长13尺,水深为12尺,
故答案为:12.
17.解:(1)连接AC,
因为∠B=90°,所以直角△ABC中,由勾股定理得:
AC2=AB2+BC2,
AC2=42+32,
AC2=25,
∴AC=5m,又CD=12m,AD=13m,
所以△ACD中,AC2+CD2=AD2,
所以△ACD是直角三角形;
(2)S四边形ABCD=AC CD+AB BC
S四边形ABCD=×5×12+×4×3
=30+6
=36(m2),
答:该花圃的面积为36m2.
18.解:(1)猜想:若∠C为锐角时,a2+b2>c2,若∠C为钝角时,a2+b2<c2;
(2)当∠C为锐角时,a2+b2>c2,证明如下:
如图,过点A作AD⊥CB于点D,设CD=x,则BD=a﹣x,
在直角三角形ACD中,AD2=b2﹣x2,
在直角三角形ABD中,AD2=c2﹣(a﹣x)2,
∴b2﹣x2=c2﹣(a﹣x)2,即a2+b2=c2+2ax,
∵a>0,x>0,
∴a2+b2>c2,
当∠C为钝角时,a2+b2<c2,证明如下:
如图,过点A作BC的垂线交BC的延长线于点M,CM=y,则BM=a+y,
在直角三角形ACM中,AM2=b2﹣y2,
在直角三角形ABM中,AM2=c2﹣(a+y)2,
∴b2﹣y2=c2﹣(a+y)2,即a2+b2=c2﹣2ay,
∵a>0,y>0,
∴a2+b2<c2.
19.解:(1)由题意可得:RP=12×1.5=18(海里),PQ=16×1.5=24(海里);
(2)能,
理由:∵RP=12×1.5=18海里,PQ=16×1.5=24海里,QR=30海里,
∵182+242=302,
∴△RPQ是直角三角形,
∴∠RPQ=90°,
∵“综合执法1号”沿北偏东61°方向航行,
∴∠QPS=61°,
∴∠SPR=90°﹣61°=29°,
∴“综合执法2号”沿北偏西29°方向航行方向航行.
20.解:小明能听到宣传,
理由:∵村庄A到公路MN的距离为600米<1000米,
∴小明能听到宣传;
如图:假设当宣讲车行驶到P点开始小明听到广播,行驶到Q点小明听不到广播,
则AP=AQ=1000米,AB=600米,
∴BP=BQ==800(米),
∴PQ=1600米,
∴小明听到广播的时间为:1600÷250=6.4(分钟),
∴他总共能听到6.4分钟的广播.
21.解:(1)∵OA=16×1.5=24,OB=12×1.5=18,AB=30,
∴OA2+OB2=AB2,
∴△AOB是直角三角形,
∴∠AOB=90°,
∵“远航”号沿东北方向航行,
∴∠AON=45°,
∴∠BON=90°﹣45°=45°,
∴“海天”号沿西北方向航行;
(2)过点F作FD⊥PE于D,
OF=16×2=32,
∵∠NOF=60°,
∴∠FOD=90°﹣60°=30°,
∴FD=,
∴16÷80=0.2(小时),
∵0.2<0.5,
∴能在半小时内回到海岸线.
22.解:(1)∵△ABC≌△DEF,
∴∠EDF=∠CAB,
∵∠EDF+∠CAE=90°,
∴∠ACE+∠CAB=90°,
∴∠AGC=90°,
∴∠AGE=180°﹣∠AGC=90°;
∴DE⊥AB,
∴S四边形ADBE=S△ACB+S△ABE=AB DG+AB EG=AB (DG+EG)=AB DE=c2,
故答案为:90,;
(2)∵四边形ACBE的面积=S△ACB+S△ABE=AB DG+AB EG=AB (DG+EG)=AB DE=c2,
四边形ACBE的面积=S四边形ACFE+S△EFB=×(AC+EF) CF+BF EF=(b+a)b+(a﹣b) a=b2+ab+a2﹣ab=a2+b2,
∴c2=a2+b2,
即a2+b2=c2.
23.解:(1)∵CD2+AD2=144+81=225,AC2=225,
∴CD2+AD2=CA2,
∴△△ADC是直角三角形,
∴∠ADC=90°,
∴CD⊥AB,
∴∠ADC=90°,
∴BD==16,
∴AB=AD+DB=16+9=25,
∴△ABC的面积=×25×12=150;
(2)过C作CD⊥BA的延长线于点D,
∵CD⊥AB,
∴∠CDB=90°,
设AD为x,DB=(x+11),由勾股定理得:CD2=AC2﹣AD2,CD2=BC2﹣DB2,
即AC2﹣AD2=BC2﹣DB2,
则132﹣x2=202﹣(x+11)2,
解得:x=5,
∴CD===12,
∴△ABC的面积= AB CD=×11×12=66.
