沪科版数学九年级上册 23.2 解直角三角形课件(共18张PPT)
文档属性
| 名称 | 沪科版数学九年级上册 23.2 解直角三角形课件(共18张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-02 14:41:50 | ||
图片预览




文档简介
(共18张PPT)
23.2 解直角三角形及其应用
第1课时 解直角三角形
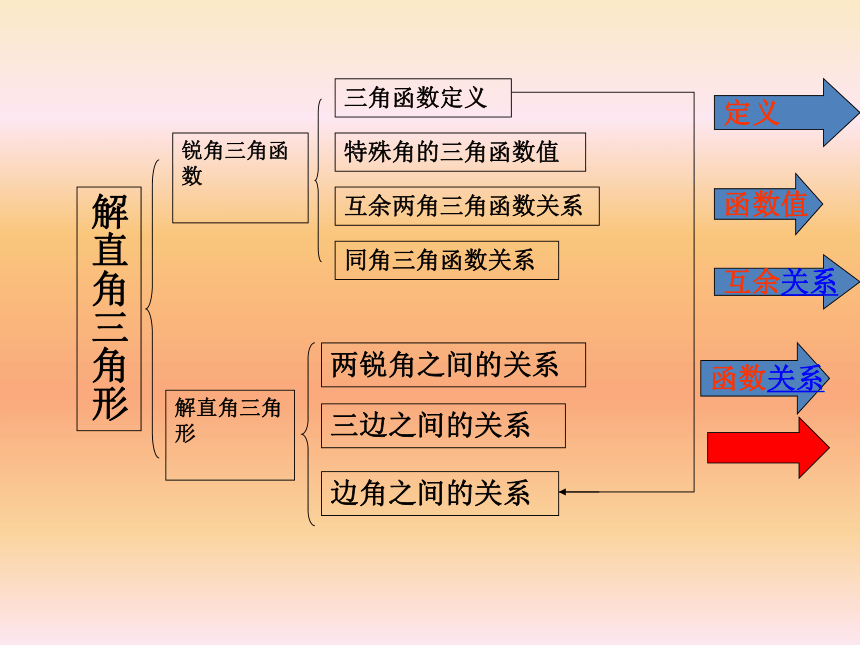
解直角三角形
锐角三角函数
解直角三角形
三角函数定义
特殊角的三角函数值
互余两角三角函数关系
同角三角函数关系
两锐角之间的关系
三边之间的关系
边角之间的关系
定义
函数值
互余关系
函数关系
1.理解直角三角形中边与边之间的关系,角与角之间的关系和边与角之间的关系.
2.会运用勾股定理、直角三角形的两个锐角互余,以及锐角三角函数解直角三角形.
3.通过综合运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形,逐步培养分析问题、解决问题的能力.
学习目标
自主学习,感知教材
1、带着目标阅读课本124到125页。
2、小组交流自学过程的收获与疑惑。
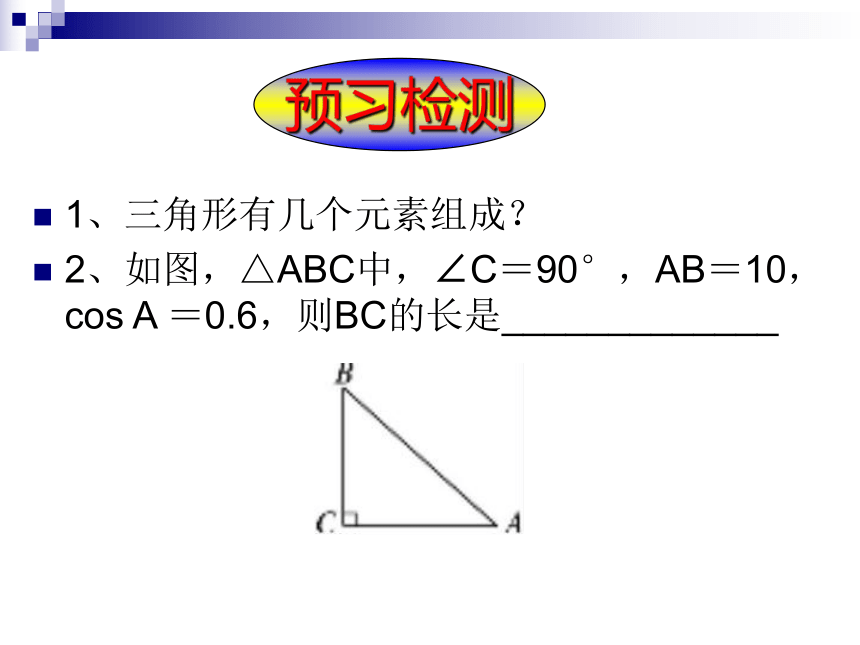
1、三角形有几个元素组成?
2、如图,△ABC中,∠C=90°,AB=10,cos A =0.6,则BC的长是_____________
预习检测
知识生成
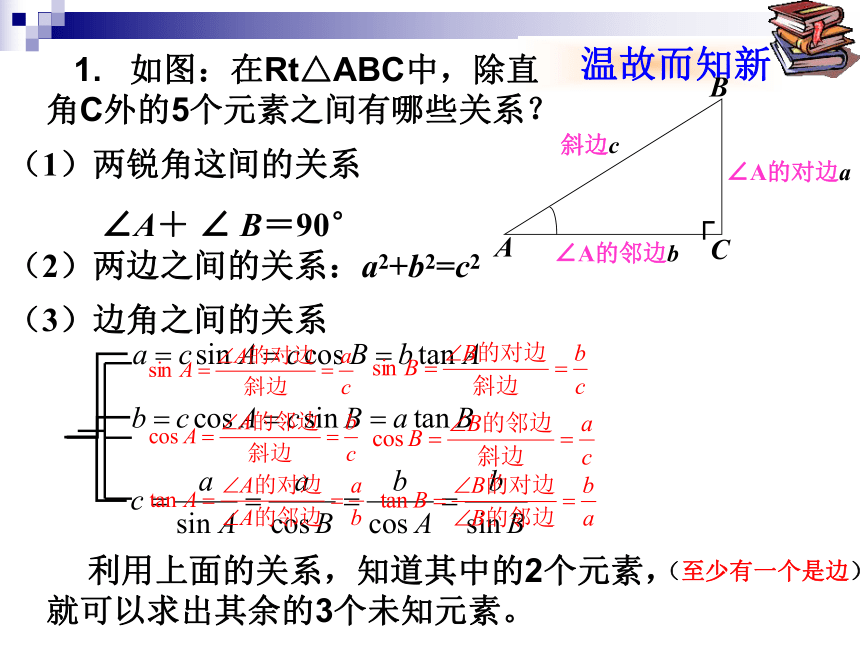
(1)两锐角这间的关系
∠A+ ∠ B=90°
(2)两边之间的关系:a2+b2=c2
(3)边角之间的关系
温故而知新
A
B
∠A的对边a
C
∠A的邻边b
┌
斜边c
1. 如图:在Rt△ABC中,除直角C外的5个元素之间有哪些关系?
利用上面的关系,知道其中的2个元素,
就可以求出其余的3个未知元素。
(至少有一个是边)
2.定义:
一般地,直角三角形中,除直角外,共有5个元素,即3条边和2个锐角,由直角三角形中除直角外的已知元素,求出其余元素的过程,叫做解直角三角形
典例分析
解直角三角形的原则:
(1)有角先求角,无角先求边
(2)有斜用弦, 无斜用切;
宁乘毋除, 取原避中。
例1:在Rt△ABC中,∠C=900,AC= ,BC= ,解这个直角三角形。
例2:在Rt△ABC中, ∠C=900, ∠ B=300,b=20,解这个直角三角形。(结果保留小数点后一位)
跟踪练习
思考:
在解直角三角形过程中需要注意哪些问题?
1、在下列直角三角形中不能求解的是( )
A、已知一直角边一锐角
B、已知一斜边一锐角
C、已知两边 D、已知两角
2、在Rt△ABC中,∠C=90°,根据下列条件解 直角三角形: (1)a=3,b=3
(2)∠B=60°, b=3.
D
当堂检测
小结
谈谈通过本节课的学习有哪些收获与困惑?
谢谢!再见
23.2 解直角三角形及其应用
第1课时 解直角三角形
解直角三角形
锐角三角函数
解直角三角形
三角函数定义
特殊角的三角函数值
互余两角三角函数关系
同角三角函数关系
两锐角之间的关系
三边之间的关系
边角之间的关系
定义
函数值
互余关系
函数关系
1.理解直角三角形中边与边之间的关系,角与角之间的关系和边与角之间的关系.
2.会运用勾股定理、直角三角形的两个锐角互余,以及锐角三角函数解直角三角形.
3.通过综合运用勾股定理,直角三角形的两个锐角互余及锐角三角函数解直角三角形,逐步培养分析问题、解决问题的能力.
学习目标
自主学习,感知教材
1、带着目标阅读课本124到125页。
2、小组交流自学过程的收获与疑惑。
1、三角形有几个元素组成?
2、如图,△ABC中,∠C=90°,AB=10,cos A =0.6,则BC的长是_____________
预习检测
知识生成
(1)两锐角这间的关系
∠A+ ∠ B=90°
(2)两边之间的关系:a2+b2=c2
(3)边角之间的关系
温故而知新
A
B
∠A的对边a
C
∠A的邻边b
┌
斜边c
1. 如图:在Rt△ABC中,除直角C外的5个元素之间有哪些关系?
利用上面的关系,知道其中的2个元素,
就可以求出其余的3个未知元素。
(至少有一个是边)
2.定义:
一般地,直角三角形中,除直角外,共有5个元素,即3条边和2个锐角,由直角三角形中除直角外的已知元素,求出其余元素的过程,叫做解直角三角形
典例分析
解直角三角形的原则:
(1)有角先求角,无角先求边
(2)有斜用弦, 无斜用切;
宁乘毋除, 取原避中。
例1:在Rt△ABC中,∠C=900,AC= ,BC= ,解这个直角三角形。
例2:在Rt△ABC中, ∠C=900, ∠ B=300,b=20,解这个直角三角形。(结果保留小数点后一位)
跟踪练习
思考:
在解直角三角形过程中需要注意哪些问题?
1、在下列直角三角形中不能求解的是( )
A、已知一直角边一锐角
B、已知一斜边一锐角
C、已知两边 D、已知两角
2、在Rt△ABC中,∠C=90°,根据下列条件解 直角三角形: (1)a=3,b=3
(2)∠B=60°, b=3.
D
当堂检测
小结
谈谈通过本节课的学习有哪些收获与困惑?
谢谢!再见
