4.5最小公倍数(课件)- 数学五年级下册(共26张PPT)人教版
文档属性
| 名称 | 4.5最小公倍数(课件)- 数学五年级下册(共26张PPT)人教版 |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-01 08:56:13 | ||
图片预览




文档简介
(共26张PPT)
人教版五年级数学下册
最小公倍数
教学目标:
1、掌握公倍数、最小公倍数两个概念。
2、理解求最小公倍数的算理,掌握求最小公倍数的方法。
重点: 建立公倍数和最小公倍数的概念,掌握求两个数最小公倍数的方法。
难点:用不同的方法寻找最小公倍数
一、自主探究,建立概念
导学提示:用列举法求公倍数和最小公倍数。
任务:1、4和6的公倍数有哪些?用你喜欢的方法试着找一找。
2、你还能说出既是4又是6的倍数的数吗?(48,60 ……)
找得完吗?找不完我们用什么表示呢?
3、你能找到4和6的最大公倍数吗?
如果找不到最大的,我们可以找到它们最小的公倍数吗?
4、用自己的话说一说什么是公倍数和最小公倍数。.
5、请你向学习最大公因数那样,用几何图的方式表示出4和
6的公倍数和最小公倍数。
流程:独学—交流---汇报
评价:自学认真,交流积极,展示精彩。
奖励:表现优秀奖励星星一颗。
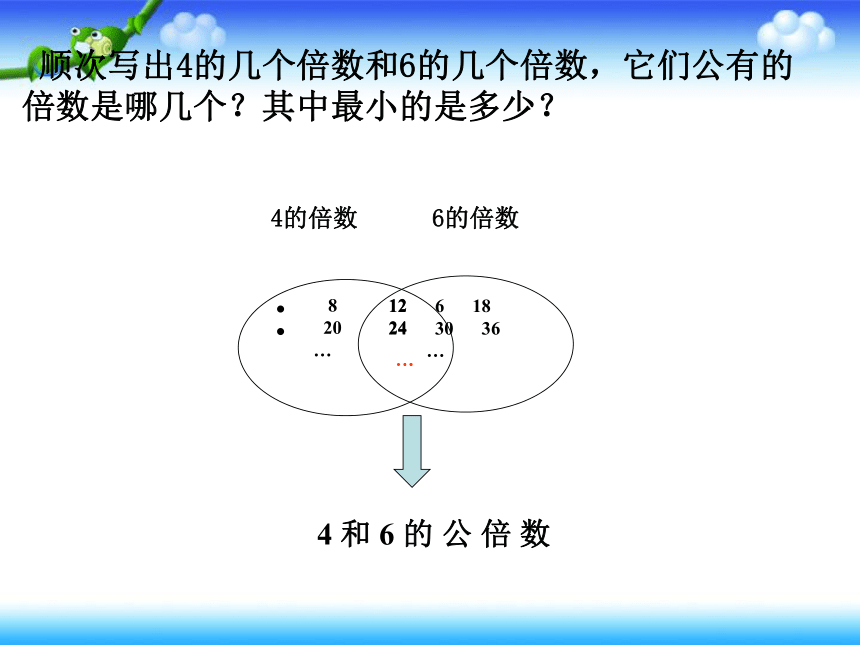
顺次写出4的几个倍数和6的几个倍数,它们公有的
倍数是哪几个?其中最小的是多少?
4的倍数
8 12
20 24
…
6的倍数
12 6 18
24 30 36
…
顺次写出4的几个倍数和6的几个倍数,它们公有的
倍数是哪几个?其中最小的是多少?
4的倍数
8 12
20 24
…
6的倍数
12 6 18
24 30 36
…
顺次写出4的几个倍数和6的几个倍数,它们公有的
倍数是哪几个?其中最小的是多少?
4的倍数
8 12
20 24
…
6的倍数
12 6 18
24 30 36
…
顺次写出4的几个倍数和6的几个倍数,它们公有的
倍数是哪几个?其中最小的是多少?
4的倍数
8 12
20 24
…
6的倍数
12 6 18
24 30 36
…
顺次写出4的几个倍数和6的几个倍数,它们公有的
倍数是哪几个?其中最小的是多少?
4的倍数
8 12
20 24
…
6的倍数
12 6 18
24 30 36
…
顺次写出4的几个倍数和6的几个倍数,它们公有的
倍数是哪几个?其中最小的是多少?
4的倍数
8 12
20 24
…
6的倍数
12 6 18
24 30 36
…
顺次写出4的几个倍数和6的几个倍数,它们公有的
倍数是哪几个?其中最小的是多少?
4的倍数
8 12
20 24
…
6的倍数
12 6 18
24 30 36
…
4 和 6 的 公 倍 数
…
②4的倍数:4,8,12,16,20,24,28,32,36……
6的倍数: 6,12,18,24,30,36,42,48 ……
① 4的倍数:4,8,12,16,20,24,28,32,36
6的倍数: 6,12,18,24,30,36,42,48,……
12,24,36,48,60 ……这些数就叫做4和6的公倍数。
4的倍数
6的倍数
4,8,16,20,
28,32,40,
……
12,24,
36,
6,18,
30,42,……
……
4和6的公倍数,
其中12是它们的最小公倍数。
几个数公有的倍数,叫做这几个数的公倍数,其中最小的一个,叫做这几个数的最小公倍数
,……
两个数有没有最大的公倍数?
因为每一个数的倍数的个数都是无限的,所以两个数的公倍数的个数也是无限的.因此,两个数没有最大的倍数.
50以内4和6的公倍数有几个?最大的是几?
50以内4和6的公倍数有4个:12、24 、36、 48
最大的是:48
如果给定一个范围,最大公倍数是存在的
二、自主探究,掌握方法
导学提示二:求两个数的最小公倍数的方法
任务:1.、请你用自己喜欢的方式找一找6和8的最小公倍数。
2、除了24和48,你还能找到更多的6和8的公倍数吗?时间1分钟,看看哪个同学找到得多。
3、 请找到6和8的倍数最多的同学进行展示。
问题:你怎么找得这么快又这么准呢?有什么好方法吗?.
4、两个数的公倍数和它们的最小公倍数之间有什么关系呢?请你自己举例验证一下。
流程:独学—交流---汇报
评价:自学认真,交流积极,展示精彩。
奖励:表现优秀奖励星星一颗。
②筛选法:
6的倍数:6,12,18,24,30,36,42,48 ……
其中24,48也是8的倍数,其中24最小。
①排列法:
6的倍数:6,12,18,24,30,36,42,48 ……
8的倍数:8,16,24,32,40,48 ……
6和8的公倍数:24,48 ……
最小公倍数是24。
我们也可以利用分解质因数的方法,比较简便
地求出两个数的最小公倍数。
例如:
60 = 2×2×3×5
42 = 2×3×7
60 和 42 的最小公倍数 = 2×3×2×5×7 = 420。
60和42公有的质因数
60独有的质因数
42独有的质因数
用分解质因数的方法求下列每组数的最小公倍数。
12和15
12=
15=
2×2×3
3×5
12和15的最小公倍数:
3×2×2×5=60
用短除法找两个数的最小公倍数
60 42
2
30
21
3
10
7
60和42的最小公倍数:
2×3×10×7=420
60 = 2×2×3×5
42 = 2×3×7
[60 ,42] = 2×3×2×5×7 = 420
自学提示:
①每次用什么做除数去除。
②除到什么时候为止。
③怎样求出两个数的最小公倍数。
求两个数的最小公倍数,先用这两个数公有的质因数连续去除(一般从最小的开始),一直除到所得的商是互质数为止,然后把所有的除数和最后的两个商连乘起来.
导学提示三:求两个数的最小公倍数的特殊情况
任务: 找出下列每组数的最小公倍数,你有什么发现?
(1)、3和6 2和8 (2)、5和6 4和9
1、找出每组数的最小公倍数。
2、观察每组中两个数的特点。
3、探究每组中两个数的最小公倍数与这两个数的关系。
流程:独学—交流---汇报
评价:自学认真,交流积极,展示精彩。
奖励:表现优秀奖励星星一颗。
3和6的最小公倍数是6,2和8的最小公倍数是8。
5和6的最小公倍数是30,4和9的最小公倍数是36。
总结提升规律:
如果两个数互质,最小公倍数是它们的乘积;
如果两个数是倍数关系,较大数是它们的最小公倍数。
1. 下面每组数的公倍数中有没有 36 有没有48 有
没有 84
6 和 18 21 和 14 12 和 8 9和24
36是6和18的公倍数。
84是21和14的公倍数。
48是12和8的公倍数。
三、巩固练习,提升认识
流程:独立完成,快速抢答 评价:反应迅速,回答正确
9和6
7和8
6和10
15和12
2、求最小公倍数
9和6的最小公倍数是18
7和8的最小公倍数是56
6和10的最小公倍数是30
15和12的最小公倍数是60
流程:独立思考,交流汇报,
评价:回答正确,表述清楚
3. 先分类,再求下列每组数的最小公倍数。
6 和 18 9 和 11 6 和 15
4 和 5 12 和 24 4 和 10
如果两个数成倍数关系,它们的最小公倍数是较大数
如果两个数的公因数只有1,它们的最小公倍数是两个数的积。
如果a是b的倍数,那么a和b的最小公倍数是( )
a
流程:组内交流,分组汇报
评价:分工明确,表述清楚的奖励星星一颗
4、判 断
1.两个数成倍数关系,其中一个数一定是这两个数的
最小公倍数。
2.两个数的公因数只有1,这两个数的最小公倍数就是1。
3.两个数的最小公倍数一定大于这两个数的最大公因数。
4.两个数的最小公倍数一定比这两个数都大。
5.两个数的积不一定是这两个数的公倍数。
√
×
×
×
×
不同
一定
有可能等于较大数
6、两个数的积一定是这两个数的最小公倍数
例如:2和4的积是8,但是2和4的最小公倍数是4
×
流程:独立完成,快速抢答 评价:反应迅速,回答正确
7:14
7:21
7:28
7:35
7:42
7:49
7:56
7:16
7:24
7:32
7:40
7:48
7:56
8:04
求7和8的最小公倍数是56.
7时+56分=7时56分。
流程:组内交流,分组汇报
评价:分工明确,表述清楚的奖励星星一颗
6和8的最小公倍数是24。
7月31日+24日=8月24日。
流程:
1、独立思考解决问题。
2、小组内交流思考方法。
3、全班交流展示、分享。
评价:自学认真,交流积极,展示精彩
四、反思回顾,提升认识
通过今天的学习你有什么收获?你还有什么问题吗?
表述清楚,明白
五、课后延伸
有一包糖果,无论是分给8个人,还是分给10个人,都能正好分完。这包糖果至少有多少块?
如果把“正好分完”改成“都剩3块”,这包糖至少有多少块?为什么?
人教版五年级数学下册
最小公倍数
教学目标:
1、掌握公倍数、最小公倍数两个概念。
2、理解求最小公倍数的算理,掌握求最小公倍数的方法。
重点: 建立公倍数和最小公倍数的概念,掌握求两个数最小公倍数的方法。
难点:用不同的方法寻找最小公倍数
一、自主探究,建立概念
导学提示:用列举法求公倍数和最小公倍数。
任务:1、4和6的公倍数有哪些?用你喜欢的方法试着找一找。
2、你还能说出既是4又是6的倍数的数吗?(48,60 ……)
找得完吗?找不完我们用什么表示呢?
3、你能找到4和6的最大公倍数吗?
如果找不到最大的,我们可以找到它们最小的公倍数吗?
4、用自己的话说一说什么是公倍数和最小公倍数。.
5、请你向学习最大公因数那样,用几何图的方式表示出4和
6的公倍数和最小公倍数。
流程:独学—交流---汇报
评价:自学认真,交流积极,展示精彩。
奖励:表现优秀奖励星星一颗。
顺次写出4的几个倍数和6的几个倍数,它们公有的
倍数是哪几个?其中最小的是多少?
4的倍数
8 12
20 24
…
6的倍数
12 6 18
24 30 36
…
顺次写出4的几个倍数和6的几个倍数,它们公有的
倍数是哪几个?其中最小的是多少?
4的倍数
8 12
20 24
…
6的倍数
12 6 18
24 30 36
…
顺次写出4的几个倍数和6的几个倍数,它们公有的
倍数是哪几个?其中最小的是多少?
4的倍数
8 12
20 24
…
6的倍数
12 6 18
24 30 36
…
顺次写出4的几个倍数和6的几个倍数,它们公有的
倍数是哪几个?其中最小的是多少?
4的倍数
8 12
20 24
…
6的倍数
12 6 18
24 30 36
…
顺次写出4的几个倍数和6的几个倍数,它们公有的
倍数是哪几个?其中最小的是多少?
4的倍数
8 12
20 24
…
6的倍数
12 6 18
24 30 36
…
顺次写出4的几个倍数和6的几个倍数,它们公有的
倍数是哪几个?其中最小的是多少?
4的倍数
8 12
20 24
…
6的倍数
12 6 18
24 30 36
…
顺次写出4的几个倍数和6的几个倍数,它们公有的
倍数是哪几个?其中最小的是多少?
4的倍数
8 12
20 24
…
6的倍数
12 6 18
24 30 36
…
4 和 6 的 公 倍 数
…
②4的倍数:4,8,12,16,20,24,28,32,36……
6的倍数: 6,12,18,24,30,36,42,48 ……
① 4的倍数:4,8,12,16,20,24,28,32,36
6的倍数: 6,12,18,24,30,36,42,48,……
12,24,36,48,60 ……这些数就叫做4和6的公倍数。
4的倍数
6的倍数
4,8,16,20,
28,32,40,
……
12,24,
36,
6,18,
30,42,……
……
4和6的公倍数,
其中12是它们的最小公倍数。
几个数公有的倍数,叫做这几个数的公倍数,其中最小的一个,叫做这几个数的最小公倍数
,……
两个数有没有最大的公倍数?
因为每一个数的倍数的个数都是无限的,所以两个数的公倍数的个数也是无限的.因此,两个数没有最大的倍数.
50以内4和6的公倍数有几个?最大的是几?
50以内4和6的公倍数有4个:12、24 、36、 48
最大的是:48
如果给定一个范围,最大公倍数是存在的
二、自主探究,掌握方法
导学提示二:求两个数的最小公倍数的方法
任务:1.、请你用自己喜欢的方式找一找6和8的最小公倍数。
2、除了24和48,你还能找到更多的6和8的公倍数吗?时间1分钟,看看哪个同学找到得多。
3、 请找到6和8的倍数最多的同学进行展示。
问题:你怎么找得这么快又这么准呢?有什么好方法吗?.
4、两个数的公倍数和它们的最小公倍数之间有什么关系呢?请你自己举例验证一下。
流程:独学—交流---汇报
评价:自学认真,交流积极,展示精彩。
奖励:表现优秀奖励星星一颗。
②筛选法:
6的倍数:6,12,18,24,30,36,42,48 ……
其中24,48也是8的倍数,其中24最小。
①排列法:
6的倍数:6,12,18,24,30,36,42,48 ……
8的倍数:8,16,24,32,40,48 ……
6和8的公倍数:24,48 ……
最小公倍数是24。
我们也可以利用分解质因数的方法,比较简便
地求出两个数的最小公倍数。
例如:
60 = 2×2×3×5
42 = 2×3×7
60 和 42 的最小公倍数 = 2×3×2×5×7 = 420。
60和42公有的质因数
60独有的质因数
42独有的质因数
用分解质因数的方法求下列每组数的最小公倍数。
12和15
12=
15=
2×2×3
3×5
12和15的最小公倍数:
3×2×2×5=60
用短除法找两个数的最小公倍数
60 42
2
30
21
3
10
7
60和42的最小公倍数:
2×3×10×7=420
60 = 2×2×3×5
42 = 2×3×7
[60 ,42] = 2×3×2×5×7 = 420
自学提示:
①每次用什么做除数去除。
②除到什么时候为止。
③怎样求出两个数的最小公倍数。
求两个数的最小公倍数,先用这两个数公有的质因数连续去除(一般从最小的开始),一直除到所得的商是互质数为止,然后把所有的除数和最后的两个商连乘起来.
导学提示三:求两个数的最小公倍数的特殊情况
任务: 找出下列每组数的最小公倍数,你有什么发现?
(1)、3和6 2和8 (2)、5和6 4和9
1、找出每组数的最小公倍数。
2、观察每组中两个数的特点。
3、探究每组中两个数的最小公倍数与这两个数的关系。
流程:独学—交流---汇报
评价:自学认真,交流积极,展示精彩。
奖励:表现优秀奖励星星一颗。
3和6的最小公倍数是6,2和8的最小公倍数是8。
5和6的最小公倍数是30,4和9的最小公倍数是36。
总结提升规律:
如果两个数互质,最小公倍数是它们的乘积;
如果两个数是倍数关系,较大数是它们的最小公倍数。
1. 下面每组数的公倍数中有没有 36 有没有48 有
没有 84
6 和 18 21 和 14 12 和 8 9和24
36是6和18的公倍数。
84是21和14的公倍数。
48是12和8的公倍数。
三、巩固练习,提升认识
流程:独立完成,快速抢答 评价:反应迅速,回答正确
9和6
7和8
6和10
15和12
2、求最小公倍数
9和6的最小公倍数是18
7和8的最小公倍数是56
6和10的最小公倍数是30
15和12的最小公倍数是60
流程:独立思考,交流汇报,
评价:回答正确,表述清楚
3. 先分类,再求下列每组数的最小公倍数。
6 和 18 9 和 11 6 和 15
4 和 5 12 和 24 4 和 10
如果两个数成倍数关系,它们的最小公倍数是较大数
如果两个数的公因数只有1,它们的最小公倍数是两个数的积。
如果a是b的倍数,那么a和b的最小公倍数是( )
a
流程:组内交流,分组汇报
评价:分工明确,表述清楚的奖励星星一颗
4、判 断
1.两个数成倍数关系,其中一个数一定是这两个数的
最小公倍数。
2.两个数的公因数只有1,这两个数的最小公倍数就是1。
3.两个数的最小公倍数一定大于这两个数的最大公因数。
4.两个数的最小公倍数一定比这两个数都大。
5.两个数的积不一定是这两个数的公倍数。
√
×
×
×
×
不同
一定
有可能等于较大数
6、两个数的积一定是这两个数的最小公倍数
例如:2和4的积是8,但是2和4的最小公倍数是4
×
流程:独立完成,快速抢答 评价:反应迅速,回答正确
7:14
7:21
7:28
7:35
7:42
7:49
7:56
7:16
7:24
7:32
7:40
7:48
7:56
8:04
求7和8的最小公倍数是56.
7时+56分=7时56分。
流程:组内交流,分组汇报
评价:分工明确,表述清楚的奖励星星一颗
6和8的最小公倍数是24。
7月31日+24日=8月24日。
流程:
1、独立思考解决问题。
2、小组内交流思考方法。
3、全班交流展示、分享。
评价:自学认真,交流积极,展示精彩
四、反思回顾,提升认识
通过今天的学习你有什么收获?你还有什么问题吗?
表述清楚,明白
五、课后延伸
有一包糖果,无论是分给8个人,还是分给10个人,都能正好分完。这包糖果至少有多少块?
如果把“正好分完”改成“都剩3块”,这包糖至少有多少块?为什么?
