第3章 数据的集中趋势和离散程度 单元测试卷 2021-2022学年苏科版九年级上册数学(word版含解析)
文档属性
| 名称 | 第3章 数据的集中趋势和离散程度 单元测试卷 2021-2022学年苏科版九年级上册数学(word版含解析) |
|
|
| 格式 | doc | ||
| 文件大小 | 288.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-03 00:00:00 | ||
图片预览





文档简介
九年级上册数学《第3章 数据的集中趋势和离散程度》
一.选择题
1.某人上山的平均速度为3km/h,沿原路下山的平均速度为5km/h,上山用1h,则此人上下山的平均速度为( )
A.4km/h B.3.75km/h C.3.5km/h D.4.5km/h
2.关于如图所示的统计图中(单位:万元),正确的说法是( )
A.第一季度总产值4.5万元 B.第二季度平均产值6万元
C.第二季度比第一季度增加5.8万元 D.第二季度比第一季度增长33.5%
3.某快递公司快递员张海六月第三周投放快递物品件数为:有1天是41件,有2天是35件,有4天是37件,这周里张海日平均投递物品件数为( )
A.36件 B.37件 C.38件 D.38.5件
4.某中学规定学生的学期体育成绩满分为100分,其中课外体育占20%,期中考试成绩占30%,期末考试成绩占50%.小彤的三项成绩(百分制)次为95,90,88,则小彤这学期的体育成绩为( )
A.89 B.90 C.92 D.93
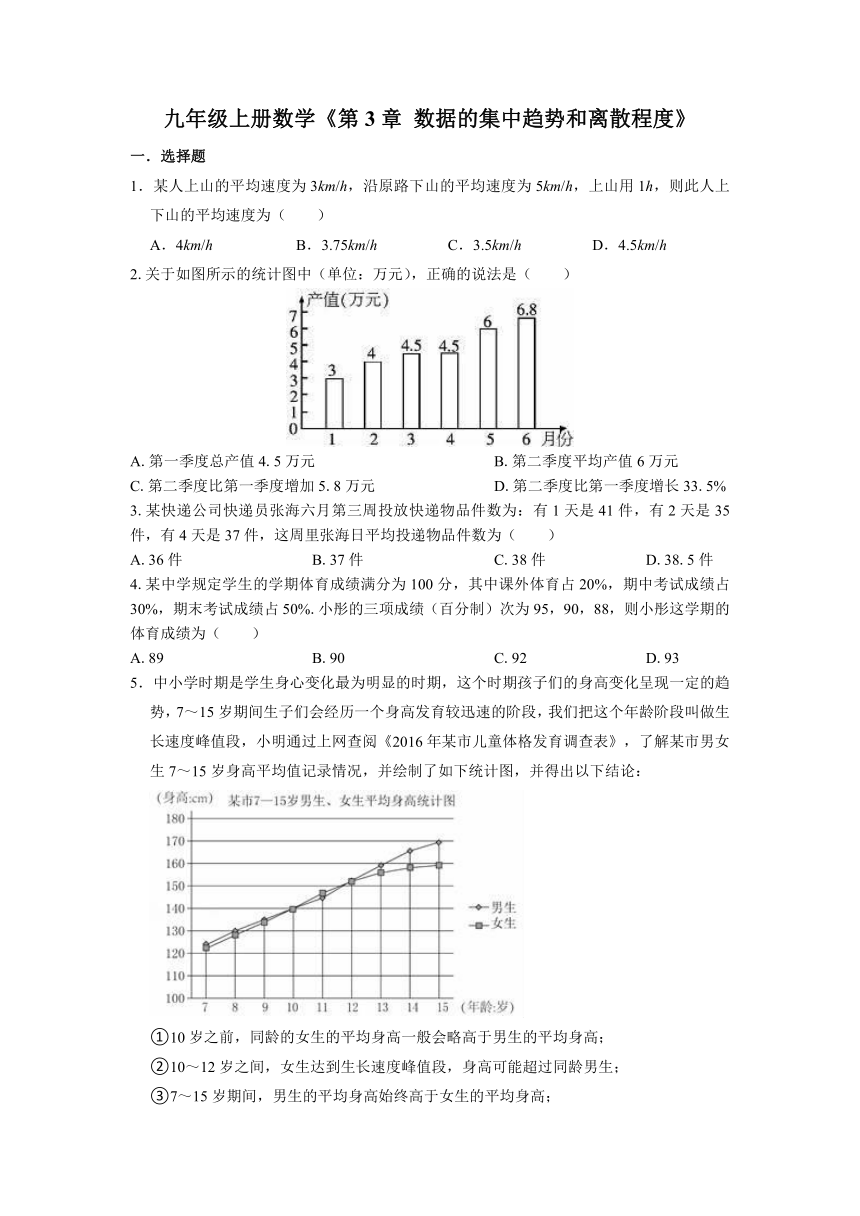
5.中小学时期是学生身心变化最为明显的时期,这个时期孩子们的身高变化呈现一定的趋势,7~15岁期间生子们会经历一个身高发育较迅速的阶段,我们把这个年龄阶段叫做生长速度峰值段,小明通过上网查阅《2016年某市儿童体格发育调查表》,了解某市男女生7~15岁身高平均值记录情况,并绘制了如下统计图,并得出以下结论:
①10岁之前,同龄的女生的平均身高一般会略高于男生的平均身高;
②10~12岁之间,女生达到生长速度峰值段,身高可能超过同龄男生;
③7~15岁期间,男生的平均身高始终高于女生的平均身高;
④13~15岁男生身高出现生长速度峰值段,男女生身高差距可能逐渐加大.
以上结论正确的是( )
A.①③ B.②③ C.②④ D.③④
6.小广,小娇分别统计了自己近5次数学测试成绩,下列统计量中能用来比较两人成绩稳定性的是( )
A.方差 B.平均数 C.众数 D.中位数
7.甲、乙、丙、丁四人进行射箭测试,每人10次射箭成绩的平均成绩都相同,方差分别是S甲2=0.65,S乙2=0.55,S丙2=0.50,S丁2=0.45,则射箭成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
8.已知一组数据:92,94,98,91,95的中位数为a,方差为b,则a+b=( )
A.98 B.99 C.100 D.102
二.填空题
9.五箱苹果的质量分别为(单位:千克)18,20,21,22,19.则这五箱苹果质量的平均数为 .
10.某生在一次考试中,语文、数学、英语三门学科的平均分为80分,物理、政治两科的平均分为85,则该生这5门学科的平均分为 分.
11.甲、乙两人进行飞镖比赛,每人各投6次,甲的成绩(单位:环)为9,8,9,6,10,6.如果甲、乙两人的平均成绩相同,乙成绩的方差为4环2,那么成绩较为稳定的是 .(填“甲”或“乙”)
12.小明参加了某电视台招聘记者的三项素质测试,成绩如下:采访写作70分,计算机操作60分,创意设计88分.若采访写作、计算机操作和创意设计的成绩按4∶1∶3计算,则他的素质测试的平均成绩为 分.
13.甲、乙两班举行数学知识竞赛,参赛学生的竞赛成绩统计结果如下表:
班级 参赛人数 平均数(分) 中位数(分) 方差(分2)
甲 45 83 86 82
乙 45 83 84 135
某同学分析上表后得到如下结论:
①甲、乙两班学生的平均成绩相同;
②乙班优秀的人数少于甲班优秀的人数(竞赛成绩≥85分为优秀);
③甲班成绩的波动性比乙班小.
上述结论中正确的是 .(填写所有正确结论的序号)
14.一个样本为1、3、2、2、a,b,c.已知这个样本的众数为3,平均数为2,那么这个样本的方差为_____.
15.有两名学员小林和小明练习射击,第一轮10枪打完后两人打靶的环数如图所示,通常新手的成绩不太稳定,那么根据图中的信息,估计小林和小明两人中新手是_______.
16.未测试两种电子表的走时误差,做了如下统计
平均数 方差
甲 0.4 0.026
乙 0.4 0.137
则这两种电子表走时稳定的是 .
三.解答题
17.将若干由1开始的连续自然数写在纸上,然后删去其中一个数,则余下的数的平均数为53,问删去的那个数是多少?
18.某工厂的一台机床,将生产的毛坯加工成直径为10cm的圆孔零件,生产质量的指标是合格品的圆孔直径不超出±0.01的误差,否则为次品.现抽样50件产品,测得产品的圆孔直径数据如下表所示:
圆孔的直径(cm) 9.97 9.98 9.99 10.00 10.01 10.02 10.03
个数 2 3 8 12 18 4 3
求这批产品的众数、中位数、平均数和合格率.
19.甲、乙两名学生参加数学素质测试(有四项),每项测试成绩(单位:分)采用百分制,成绩如表:
学生 数与代数 空间与图形 统计与概率 综合与实践 平均成绩 众数 中位数 方差
甲 95 90 a 85 x b 90 12.5
乙 90 c 80 95 x 95 d 37.5
(1)根据表中信息判断哪个学生数学素质测试成绩更稳定?请说明理由.
(2)表格中的数据a= ;b= ;c= ;d= ;
(3)若数学素质测试的四个项目的重要程度有所不同,而给予“数与代数”、“空间与图形”、“统计与概率”、“综合与实践”四个项目在综合成绩中所占的比例分别为40%,30%,10%,20%.计算得到乙的综合成绩为91.5分,请你计算甲的综合成绩,并说明谁的综合成绩更好?
20.甲、乙、丙三位运动员在相同条件下各射靶10次,每次射靶的成绩如下:
甲:9,10,8,5,7,8,10,8,8,7;
乙:5,7,8,7,8,9,7,9,10,10;
丙:7,6,8,5,4,7,6,3,9,5.
(1)根据以上数据完成下表:
平均数 中位数 方差
甲 8 8
乙 8 8 2.2
丙 6 3
(2)依据表中数据分析,哪位运动员的成绩最稳定,并简要说明理由.
21.甲、乙两位同学进行投篮比赛,每人在相同时间内分别投6场,下表是甲、乙两位同学每场投中篮球个数的统计情况.
对象 一 二 三 四 五 六
甲 6 7 5 9 5 10
乙 6 5 6 7 9 9
下面是甲、乙两位同学的三种说法.
①乙:我的投篮成绩比甲稳定;
②甲:若每一场我多投中一个球,投篮成绩就比乙稳定;
③乙:若每场我投中的个数是原来的3倍,而甲每场投中的个数是原来的2倍,则我的投篮成绩的稳定程度比甲好.
请判断他们说法的正确性,并说明理由.
22.某工厂甲、乙两名工人参加操作技能培训,现分别从他们在培训期间参加的若干次测试成绩中随机抽取5次,记录如下:
甲 85 88 84 85 83
乙 83 87 84 86 85
(1)请你分别计算这两组数据的平均数;
(2)现要从中选派一人参加操作技能比赛,从统计学的角度考虑,你认为选派哪名工人参加合适?请说明理由.
23.在“全民读书月”活动中,小明调查了班级里40名同学本学期计划购买课外书的花费情况,并将结果绘制成如图所示的统计图,请根据相关信息,解答下列问题:(直接填写结果)
(1)本次调查获取的样本数据的众数是 ;
(2)这次调查获取的样本数据的中位数是 ;
(3)若该校共有学生1000人,根据样本数据,估计本学期计划购买课外书花费50元的学生有 人.
参考答案与试题解析
一.选择题
1.解:根据题意得,路程s=上山的平均速度v1×上山时间t1=3km/h×1h=3km,
∴下山时间t2===0.6h,
∴平均速度v==3.75km/h,
故选:B.
2.【答案】C
【解析】解:依次分析选项可得:A、第一季度总产值万元,错误;B、第二季度平均产值为万元,错误;C、第二季度比第一季度增加万元,正确;D、第二季度比第一季度增长,错误;故选:C.
【考点】条形统计图的综合运用
3.【答案】B
【解析】解:由题意可得,这周里张海日平均投递物品件数为:(件).故选:B.
【考点】加权平均数
4.【答案】B
【解析】解:根据题意得:(分).即小彤这学期的体育成绩为90分.故选:B.
【考点】加权平均数
5.解:①10岁之前,同龄的女生的平均身高与男生的平均身高基本相同,故该说法错误;
②10~12岁之间,女生达到生长速度峰值段,身高可能超过同龄男生,故该说法正确;
③7~15岁期间,男生的平均身高不一定高于女生的平均身高,如11岁的男生的平均身高低于女生的平均身高,故该说法错误;
④13~15岁男生身高出现生长速度峰值段,男女生身高差距可能逐渐加大,故该说法正确.
故选:C.
6.A
【解析】平均数,众数,中位数都是反映数字集中趋势的数量,方差是反映数据离散水平的数据,也就会说反映数据稳定程度的数据是方差
故选A
7.D
【解析】∵射箭成绩的平均成绩都相同,方差分别是S甲2=0.65,S乙2=0.55,S丙2=0.50,S丁2=0.45,
∴S2甲>S2乙>S2丙>S2丁,
∴射箭成绩最稳定的是丁;
故选D.
8.C
【解析】数据:92,94,98,91,95从小到大排列为91,92,94,95,98,处于中间位置的数是94,
则该组数据的中位数是94,即a=94,
该组数据的平均数为×(92+94+98+91+95)=94,
其方差为×[(92﹣94)2+(94﹣94)2+(98﹣94)2+(91﹣94)2+(95﹣94)2]
=6,所以b=6,
所以a+b=94+6=100,
故选C.
二.填空题
9.解:这五箱苹果质量的平均数为:=20.
故答案为:20.
10.解:由题意知,语文、数学、英语三门学科的总分=3×80=240,物理、政治两科的总分=85×2=170,
∴该生这5门学科的平均分=(240+170)÷5=410÷5=82(分).
故填82.
11.解:(2×2+3×2+4×10+5×6)÷20
=(4+6+40+30)÷20
=80÷20
=4(次).
∴这20名男生该周参加篮球运动次数的平均数是4次.
故答案为:4.
12.8.5 8
【解析】∵一名射击运动员连续打靶8次,成绩排序为:7,8,8,8,9,9,10,10,(单位:环),
∴中位数为:(8+9)÷2=8.5(环),
∵8环出现的次数最多,
∴众数为:8(环),
故答案是:8.5,8.
13.1 ; l.1.
【解析】由统计图可知,共有(人),中位数应为第20与第21个数的平均数,而第20个数和第2l个数都是1小时,则中位数是1小时,被调查学生阅读时间的平均数是(时).
12.[答案] 75.5
[解析] 根据题意,得(70×4+60+88×3)÷8=75.5(分).
13.[答案] ①②③
[解析] 由表格可知,甲、乙两班学生的平均成绩相同;
根据中位数可以确定,乙班优秀的人数少于甲班优秀的人数;
根据方差可知,甲班成绩的波动性比乙班小.故①②③正确.故答案为①②③.
14.解:(1)这10名男生立定跳远成绩的极差是2.60-1.87=0.73(米),
这10名男生立定跳远成绩的平均数是
(1.96+2.38+2.56+2.04+2.34+2.17+2.60+2.26+1.87+2.32)=2.25(米).
(2)这10名男生的立定跳远得分(单位:分)依次是
7,10,10,8,10,8,10,9,6,9.按从小到大排列为6,7,8,8,9,9,10,10,10,10.故这10名男生立定跳远得分的中位数是9分,众数是10分.
(3)因为抽查的10名男生中得分为9分(含9分)以上的有6人,
所以480×=288(人),
所以估计这480名男生中得优秀的人数是288人.
14..
【解析】解:因为众数为3,可设a=3,b=3,c未知
平均数=(1+3+2+2+3+3+c)=2,解得c=0
根据方差公式S2= [(1-2)2+(3-2)2+(2-2)2+(2-2)2+(3-2)2+(3-2)2+(0-2)2]=
故答案为:.
15.小林
【解析】观察图形可知,小林的成绩波动比较大,故小林是新手.
故答案是:小林.
16.甲
【解析】∵甲的方差是0.026,乙的方差是0.137,
0.026<0.137,
∴这两种电子表走时稳定的是甲;
故答案为甲.
三.解答题
17.解:1,2,3,4,….,105的平均数是53,
1,2,3,4,….,106的平均数是53.5
它应该有105个或106个连续数.
(1)由于减去一个数的平均为53,当n=105个,但104×53不是整数,故否定了有105个数.
(2)当106个数时,很明显不会删去106,故应是1﹣105中其中一个数,考虑平均数的分数部,由于是105个数的平均,故将=,当中表示删去的数为106﹣45=61,或1+2+3+…+106=5671,
当减去一个数后,平均为53,n=105,
和=53×105=5610,
所以减去的一个数应是5671﹣5610=61.
答:删去的那个数是61.
18.解:10.01出现的次数最多,为18次,所以众数是10.01;
50个数的中位数是第25个和第26个数的平均数:(10+10.01)÷2=10.005,
中位数10.005,
平均数==10.003,
合格率=(8+12+18)÷50×100%=76%.
19.解:(1)甲的数学素质测试成绩更稳定,因为甲成绩的方差小于乙成绩的方差;
(2)由表可知,乙的众数为95,
∴c=95,
乙的中位数为d==92.5,
乙的平均数为x=(90+95+80+95)=90,
∴a=90×4﹣95﹣90﹣85=90,
∴甲的众数为b=90,
故答案为:90,90,95,92.5;
(3)甲的平均成绩为95×40%+90×30%+90×10%+85×20%=91(分),
91<91.5,
所以,乙的综合成绩更好.
20.解:(1)∵甲的平均数是8,
∴甲的方差为: [(5﹣8)2+2(7﹣8)2+4(8﹣8)2+(9﹣8)2+2(10﹣8)2]=2;
把丙运动员的射靶成绩从小到大排列为:3,4,5,5,6,6,7,7,8,9,则中位数是=6;
故答案为:2,6;
(2)∵甲的方差<乙的方差<丙的方差,而方差越小,数据波动越小,
∴甲的成绩最稳定.
21.①乙的说法正确,见解析;②甲的说法是错误的,见解析;③乙的说法是不正确的,见解析.
【解析】①甲的平均成绩为(个).
甲的方差.
乙的平均成绩为(个),
乙的方差.
因为甲、乙的平均成绩相同,且,所以乙的投篮成绩比甲稳定,所以乙的说法正确.
②甲变化后的成绩为7,8,6,10,6,11,
甲变化后的平均成绩为(个),
甲变化后的方差为,
由甲的方差不变,可知甲的说法是错误的.
③甲变化后的平均成绩为(个),方差约为,乙变化后的平均成绩为(个),方差约为.因为.
所以变化后乙的投篮成绩的稳定程度没有甲的好,所以乙的说法是不正确的.
22.(1)甲平均数: 85,乙平均数: 85;(2)选派乙工人参加合适,理由见解析;
【解析】解:(1)甲平均数:×(85+88+84+85+83)=×425=85,
乙平均数:×(83+87+84+86+85)=×425=85;
(2)选派乙工人参加合适.
理由如下:S甲2=×[(85﹣85)2+(88﹣85)2+(84﹣85)2+(85﹣85)2+(83﹣85)2],
=×(0+9+1+0+4),
=2.8,
S乙2=×[(83﹣85)2+(87﹣85)2+(84﹣85)2+(86﹣85)2+(85﹣85)2],
=×(4+4+1+1+0),
=2,
∵2.8>2,
∴S甲2>S乙2,
∴乙成绩更稳定,
∴选派乙工人参加合适.
23.(1)30元;(2)50元;(3)250.
【解析】(1)花费30元的有12人,最多,故众数是30元;
(2)一共有40个数据,排序后第20、21个数据的平均数即是中位数,6+12=18<20,6+12+10=28>20,故第20、21个数据都是50元,故中位数是50元;
(3)10÷40×2400=600(人),故估计本学期计划购买课外书花费50元的学生有50人.
一.选择题
1.某人上山的平均速度为3km/h,沿原路下山的平均速度为5km/h,上山用1h,则此人上下山的平均速度为( )
A.4km/h B.3.75km/h C.3.5km/h D.4.5km/h
2.关于如图所示的统计图中(单位:万元),正确的说法是( )
A.第一季度总产值4.5万元 B.第二季度平均产值6万元
C.第二季度比第一季度增加5.8万元 D.第二季度比第一季度增长33.5%
3.某快递公司快递员张海六月第三周投放快递物品件数为:有1天是41件,有2天是35件,有4天是37件,这周里张海日平均投递物品件数为( )
A.36件 B.37件 C.38件 D.38.5件
4.某中学规定学生的学期体育成绩满分为100分,其中课外体育占20%,期中考试成绩占30%,期末考试成绩占50%.小彤的三项成绩(百分制)次为95,90,88,则小彤这学期的体育成绩为( )
A.89 B.90 C.92 D.93
5.中小学时期是学生身心变化最为明显的时期,这个时期孩子们的身高变化呈现一定的趋势,7~15岁期间生子们会经历一个身高发育较迅速的阶段,我们把这个年龄阶段叫做生长速度峰值段,小明通过上网查阅《2016年某市儿童体格发育调查表》,了解某市男女生7~15岁身高平均值记录情况,并绘制了如下统计图,并得出以下结论:
①10岁之前,同龄的女生的平均身高一般会略高于男生的平均身高;
②10~12岁之间,女生达到生长速度峰值段,身高可能超过同龄男生;
③7~15岁期间,男生的平均身高始终高于女生的平均身高;
④13~15岁男生身高出现生长速度峰值段,男女生身高差距可能逐渐加大.
以上结论正确的是( )
A.①③ B.②③ C.②④ D.③④
6.小广,小娇分别统计了自己近5次数学测试成绩,下列统计量中能用来比较两人成绩稳定性的是( )
A.方差 B.平均数 C.众数 D.中位数
7.甲、乙、丙、丁四人进行射箭测试,每人10次射箭成绩的平均成绩都相同,方差分别是S甲2=0.65,S乙2=0.55,S丙2=0.50,S丁2=0.45,则射箭成绩最稳定的是( )
A.甲 B.乙 C.丙 D.丁
8.已知一组数据:92,94,98,91,95的中位数为a,方差为b,则a+b=( )
A.98 B.99 C.100 D.102
二.填空题
9.五箱苹果的质量分别为(单位:千克)18,20,21,22,19.则这五箱苹果质量的平均数为 .
10.某生在一次考试中,语文、数学、英语三门学科的平均分为80分,物理、政治两科的平均分为85,则该生这5门学科的平均分为 分.
11.甲、乙两人进行飞镖比赛,每人各投6次,甲的成绩(单位:环)为9,8,9,6,10,6.如果甲、乙两人的平均成绩相同,乙成绩的方差为4环2,那么成绩较为稳定的是 .(填“甲”或“乙”)
12.小明参加了某电视台招聘记者的三项素质测试,成绩如下:采访写作70分,计算机操作60分,创意设计88分.若采访写作、计算机操作和创意设计的成绩按4∶1∶3计算,则他的素质测试的平均成绩为 分.
13.甲、乙两班举行数学知识竞赛,参赛学生的竞赛成绩统计结果如下表:
班级 参赛人数 平均数(分) 中位数(分) 方差(分2)
甲 45 83 86 82
乙 45 83 84 135
某同学分析上表后得到如下结论:
①甲、乙两班学生的平均成绩相同;
②乙班优秀的人数少于甲班优秀的人数(竞赛成绩≥85分为优秀);
③甲班成绩的波动性比乙班小.
上述结论中正确的是 .(填写所有正确结论的序号)
14.一个样本为1、3、2、2、a,b,c.已知这个样本的众数为3,平均数为2,那么这个样本的方差为_____.
15.有两名学员小林和小明练习射击,第一轮10枪打完后两人打靶的环数如图所示,通常新手的成绩不太稳定,那么根据图中的信息,估计小林和小明两人中新手是_______.
16.未测试两种电子表的走时误差,做了如下统计
平均数 方差
甲 0.4 0.026
乙 0.4 0.137
则这两种电子表走时稳定的是 .
三.解答题
17.将若干由1开始的连续自然数写在纸上,然后删去其中一个数,则余下的数的平均数为53,问删去的那个数是多少?
18.某工厂的一台机床,将生产的毛坯加工成直径为10cm的圆孔零件,生产质量的指标是合格品的圆孔直径不超出±0.01的误差,否则为次品.现抽样50件产品,测得产品的圆孔直径数据如下表所示:
圆孔的直径(cm) 9.97 9.98 9.99 10.00 10.01 10.02 10.03
个数 2 3 8 12 18 4 3
求这批产品的众数、中位数、平均数和合格率.
19.甲、乙两名学生参加数学素质测试(有四项),每项测试成绩(单位:分)采用百分制,成绩如表:
学生 数与代数 空间与图形 统计与概率 综合与实践 平均成绩 众数 中位数 方差
甲 95 90 a 85 x b 90 12.5
乙 90 c 80 95 x 95 d 37.5
(1)根据表中信息判断哪个学生数学素质测试成绩更稳定?请说明理由.
(2)表格中的数据a= ;b= ;c= ;d= ;
(3)若数学素质测试的四个项目的重要程度有所不同,而给予“数与代数”、“空间与图形”、“统计与概率”、“综合与实践”四个项目在综合成绩中所占的比例分别为40%,30%,10%,20%.计算得到乙的综合成绩为91.5分,请你计算甲的综合成绩,并说明谁的综合成绩更好?
20.甲、乙、丙三位运动员在相同条件下各射靶10次,每次射靶的成绩如下:
甲:9,10,8,5,7,8,10,8,8,7;
乙:5,7,8,7,8,9,7,9,10,10;
丙:7,6,8,5,4,7,6,3,9,5.
(1)根据以上数据完成下表:
平均数 中位数 方差
甲 8 8
乙 8 8 2.2
丙 6 3
(2)依据表中数据分析,哪位运动员的成绩最稳定,并简要说明理由.
21.甲、乙两位同学进行投篮比赛,每人在相同时间内分别投6场,下表是甲、乙两位同学每场投中篮球个数的统计情况.
对象 一 二 三 四 五 六
甲 6 7 5 9 5 10
乙 6 5 6 7 9 9
下面是甲、乙两位同学的三种说法.
①乙:我的投篮成绩比甲稳定;
②甲:若每一场我多投中一个球,投篮成绩就比乙稳定;
③乙:若每场我投中的个数是原来的3倍,而甲每场投中的个数是原来的2倍,则我的投篮成绩的稳定程度比甲好.
请判断他们说法的正确性,并说明理由.
22.某工厂甲、乙两名工人参加操作技能培训,现分别从他们在培训期间参加的若干次测试成绩中随机抽取5次,记录如下:
甲 85 88 84 85 83
乙 83 87 84 86 85
(1)请你分别计算这两组数据的平均数;
(2)现要从中选派一人参加操作技能比赛,从统计学的角度考虑,你认为选派哪名工人参加合适?请说明理由.
23.在“全民读书月”活动中,小明调查了班级里40名同学本学期计划购买课外书的花费情况,并将结果绘制成如图所示的统计图,请根据相关信息,解答下列问题:(直接填写结果)
(1)本次调查获取的样本数据的众数是 ;
(2)这次调查获取的样本数据的中位数是 ;
(3)若该校共有学生1000人,根据样本数据,估计本学期计划购买课外书花费50元的学生有 人.
参考答案与试题解析
一.选择题
1.解:根据题意得,路程s=上山的平均速度v1×上山时间t1=3km/h×1h=3km,
∴下山时间t2===0.6h,
∴平均速度v==3.75km/h,
故选:B.
2.【答案】C
【解析】解:依次分析选项可得:A、第一季度总产值万元,错误;B、第二季度平均产值为万元,错误;C、第二季度比第一季度增加万元,正确;D、第二季度比第一季度增长,错误;故选:C.
【考点】条形统计图的综合运用
3.【答案】B
【解析】解:由题意可得,这周里张海日平均投递物品件数为:(件).故选:B.
【考点】加权平均数
4.【答案】B
【解析】解:根据题意得:(分).即小彤这学期的体育成绩为90分.故选:B.
【考点】加权平均数
5.解:①10岁之前,同龄的女生的平均身高与男生的平均身高基本相同,故该说法错误;
②10~12岁之间,女生达到生长速度峰值段,身高可能超过同龄男生,故该说法正确;
③7~15岁期间,男生的平均身高不一定高于女生的平均身高,如11岁的男生的平均身高低于女生的平均身高,故该说法错误;
④13~15岁男生身高出现生长速度峰值段,男女生身高差距可能逐渐加大,故该说法正确.
故选:C.
6.A
【解析】平均数,众数,中位数都是反映数字集中趋势的数量,方差是反映数据离散水平的数据,也就会说反映数据稳定程度的数据是方差
故选A
7.D
【解析】∵射箭成绩的平均成绩都相同,方差分别是S甲2=0.65,S乙2=0.55,S丙2=0.50,S丁2=0.45,
∴S2甲>S2乙>S2丙>S2丁,
∴射箭成绩最稳定的是丁;
故选D.
8.C
【解析】数据:92,94,98,91,95从小到大排列为91,92,94,95,98,处于中间位置的数是94,
则该组数据的中位数是94,即a=94,
该组数据的平均数为×(92+94+98+91+95)=94,
其方差为×[(92﹣94)2+(94﹣94)2+(98﹣94)2+(91﹣94)2+(95﹣94)2]
=6,所以b=6,
所以a+b=94+6=100,
故选C.
二.填空题
9.解:这五箱苹果质量的平均数为:=20.
故答案为:20.
10.解:由题意知,语文、数学、英语三门学科的总分=3×80=240,物理、政治两科的总分=85×2=170,
∴该生这5门学科的平均分=(240+170)÷5=410÷5=82(分).
故填82.
11.解:(2×2+3×2+4×10+5×6)÷20
=(4+6+40+30)÷20
=80÷20
=4(次).
∴这20名男生该周参加篮球运动次数的平均数是4次.
故答案为:4.
12.8.5 8
【解析】∵一名射击运动员连续打靶8次,成绩排序为:7,8,8,8,9,9,10,10,(单位:环),
∴中位数为:(8+9)÷2=8.5(环),
∵8环出现的次数最多,
∴众数为:8(环),
故答案是:8.5,8.
13.1 ; l.1.
【解析】由统计图可知,共有(人),中位数应为第20与第21个数的平均数,而第20个数和第2l个数都是1小时,则中位数是1小时,被调查学生阅读时间的平均数是(时).
12.[答案] 75.5
[解析] 根据题意,得(70×4+60+88×3)÷8=75.5(分).
13.[答案] ①②③
[解析] 由表格可知,甲、乙两班学生的平均成绩相同;
根据中位数可以确定,乙班优秀的人数少于甲班优秀的人数;
根据方差可知,甲班成绩的波动性比乙班小.故①②③正确.故答案为①②③.
14.解:(1)这10名男生立定跳远成绩的极差是2.60-1.87=0.73(米),
这10名男生立定跳远成绩的平均数是
(1.96+2.38+2.56+2.04+2.34+2.17+2.60+2.26+1.87+2.32)=2.25(米).
(2)这10名男生的立定跳远得分(单位:分)依次是
7,10,10,8,10,8,10,9,6,9.按从小到大排列为6,7,8,8,9,9,10,10,10,10.故这10名男生立定跳远得分的中位数是9分,众数是10分.
(3)因为抽查的10名男生中得分为9分(含9分)以上的有6人,
所以480×=288(人),
所以估计这480名男生中得优秀的人数是288人.
14..
【解析】解:因为众数为3,可设a=3,b=3,c未知
平均数=(1+3+2+2+3+3+c)=2,解得c=0
根据方差公式S2= [(1-2)2+(3-2)2+(2-2)2+(2-2)2+(3-2)2+(3-2)2+(0-2)2]=
故答案为:.
15.小林
【解析】观察图形可知,小林的成绩波动比较大,故小林是新手.
故答案是:小林.
16.甲
【解析】∵甲的方差是0.026,乙的方差是0.137,
0.026<0.137,
∴这两种电子表走时稳定的是甲;
故答案为甲.
三.解答题
17.解:1,2,3,4,….,105的平均数是53,
1,2,3,4,….,106的平均数是53.5
它应该有105个或106个连续数.
(1)由于减去一个数的平均为53,当n=105个,但104×53不是整数,故否定了有105个数.
(2)当106个数时,很明显不会删去106,故应是1﹣105中其中一个数,考虑平均数的分数部,由于是105个数的平均,故将=,当中表示删去的数为106﹣45=61,或1+2+3+…+106=5671,
当减去一个数后,平均为53,n=105,
和=53×105=5610,
所以减去的一个数应是5671﹣5610=61.
答:删去的那个数是61.
18.解:10.01出现的次数最多,为18次,所以众数是10.01;
50个数的中位数是第25个和第26个数的平均数:(10+10.01)÷2=10.005,
中位数10.005,
平均数==10.003,
合格率=(8+12+18)÷50×100%=76%.
19.解:(1)甲的数学素质测试成绩更稳定,因为甲成绩的方差小于乙成绩的方差;
(2)由表可知,乙的众数为95,
∴c=95,
乙的中位数为d==92.5,
乙的平均数为x=(90+95+80+95)=90,
∴a=90×4﹣95﹣90﹣85=90,
∴甲的众数为b=90,
故答案为:90,90,95,92.5;
(3)甲的平均成绩为95×40%+90×30%+90×10%+85×20%=91(分),
91<91.5,
所以,乙的综合成绩更好.
20.解:(1)∵甲的平均数是8,
∴甲的方差为: [(5﹣8)2+2(7﹣8)2+4(8﹣8)2+(9﹣8)2+2(10﹣8)2]=2;
把丙运动员的射靶成绩从小到大排列为:3,4,5,5,6,6,7,7,8,9,则中位数是=6;
故答案为:2,6;
(2)∵甲的方差<乙的方差<丙的方差,而方差越小,数据波动越小,
∴甲的成绩最稳定.
21.①乙的说法正确,见解析;②甲的说法是错误的,见解析;③乙的说法是不正确的,见解析.
【解析】①甲的平均成绩为(个).
甲的方差.
乙的平均成绩为(个),
乙的方差.
因为甲、乙的平均成绩相同,且,所以乙的投篮成绩比甲稳定,所以乙的说法正确.
②甲变化后的成绩为7,8,6,10,6,11,
甲变化后的平均成绩为(个),
甲变化后的方差为,
由甲的方差不变,可知甲的说法是错误的.
③甲变化后的平均成绩为(个),方差约为,乙变化后的平均成绩为(个),方差约为.因为.
所以变化后乙的投篮成绩的稳定程度没有甲的好,所以乙的说法是不正确的.
22.(1)甲平均数: 85,乙平均数: 85;(2)选派乙工人参加合适,理由见解析;
【解析】解:(1)甲平均数:×(85+88+84+85+83)=×425=85,
乙平均数:×(83+87+84+86+85)=×425=85;
(2)选派乙工人参加合适.
理由如下:S甲2=×[(85﹣85)2+(88﹣85)2+(84﹣85)2+(85﹣85)2+(83﹣85)2],
=×(0+9+1+0+4),
=2.8,
S乙2=×[(83﹣85)2+(87﹣85)2+(84﹣85)2+(86﹣85)2+(85﹣85)2],
=×(4+4+1+1+0),
=2,
∵2.8>2,
∴S甲2>S乙2,
∴乙成绩更稳定,
∴选派乙工人参加合适.
23.(1)30元;(2)50元;(3)250.
【解析】(1)花费30元的有12人,最多,故众数是30元;
(2)一共有40个数据,排序后第20、21个数据的平均数即是中位数,6+12=18<20,6+12+10=28>20,故第20、21个数据都是50元,故中位数是50元;
(3)10÷40×2400=600(人),故估计本学期计划购买课外书花费50元的学生有50人.
同课章节目录
- 第1章 一元二次方程
- 1.1 一元二次方程
- 1.2 一元二次方程的解法
- 1.3 一元二次方程的根与系数的关系
- 1.4 用一元二次方程解决问题
- 数学活动 矩形绿地中的花圃设计
- 第2章 对称图形——圆
- 2.1 圆
- 2.2 圆的对称性
- 2.3 确定圆的条件
- 2.4 圆周角
- 2.5 直线与圆的位置关系
- 2.6 正多边形与圆
- 2.7 弧长及扇形的面积
- 2.8 圆锥的侧面积
- 数学活动 图形的密铺
- 第3章 数据的集中趋势和离散程度
- 3.1 平均数
- 3.2 中位数与众数
- 3.3 用计算器求平均数
- 3.4 方差
- 3.5 用计算器求方差
- 数学活动 估测时间
- 第4章 等可能条件下的概率
- 4.1 等可能性
- 4.2 等可能条件下的概率(一)
- 4.3 等可能条件下的概率(二)
- 数学活动 调查“小概率事件”
