1.1.3《集合的基本运算:并集与交集》课件(共17张PPT)
文档属性
| 名称 | 1.1.3《集合的基本运算:并集与交集》课件(共17张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 753.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-04 07:42:58 | ||
图片预览





文档简介
(共17张PPT)
他一起是采购了八类物品吗?
小王去采购一批物品,他采购了五类办公用品,三类电器,他一起采购了多少类物品?
假如:
办公用品类:电脑 办公桌 钢笔 纸 打印机
电器类 :彩电 洗衣机 电脑
观察下列两个集合,你能说出集合C与集合A、B之间的关系吗?
(1) A={1,3,5},B={2,4,6}
C={1,2,3,4,5,6}
(2) A={x|x是有理数},B={x|x是无理数}
C={x|x是实数}
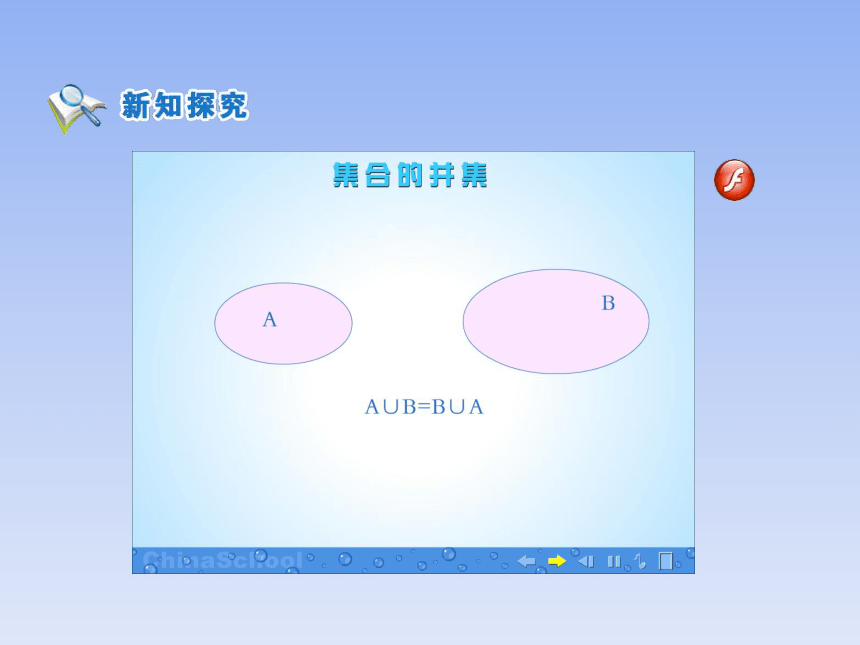
并集:
由所有属于集合A或属于集合B的元素组成的集合,称为A与B的并集(union set).
记作:A∪B (读作“A并B”)
即:
A∪B=
{x|x∈A,或x∈B}
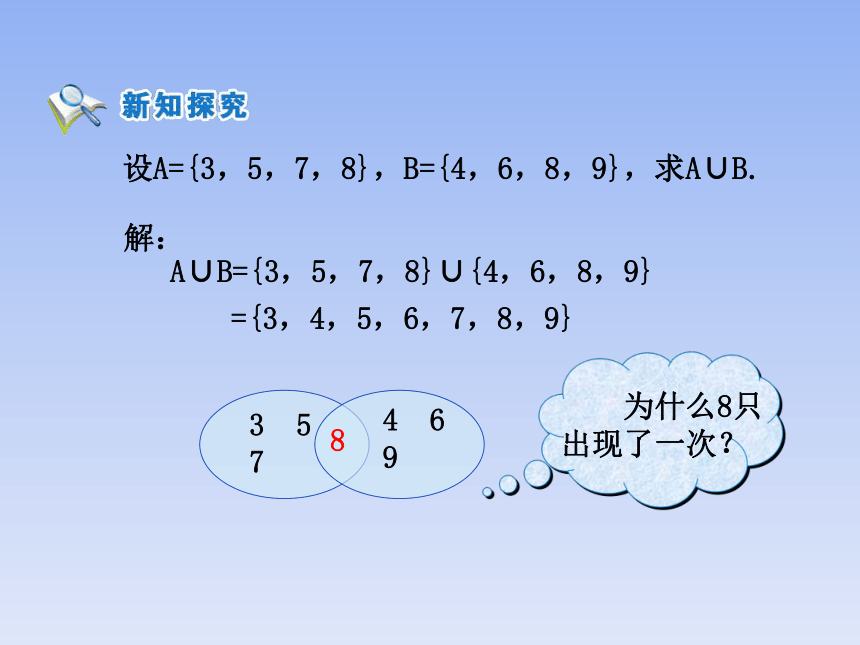
设A={3,5,7,8},B={4,6,8,9},求A∪B.
解:
A∪B={3,5,7,8}∪{4,6,8,9}
3 5
7
4 6
9
8
={3,4,5,6,7,8,9}
为什么8只出现了一次?
A={x|-1解:A∪B={x|-10
1
2
3
4
-1
-2
-3
x
A={x|-1解:A∪B={x|-1={x|-1 思考:求集合的并集是集合间的一种运算,那么,集合间还有其他的运算吗?
0
1
2
3
4
-1
-2
-3
x
观察下列两个集合,你能说出集合C与集合A、B之间的关系吗?
(1)A={2,4,6,8,10},B={3,5,8,12}
C={8}
(2)A={我们班的女同学},B={我们班的所有同学}
C={我们班的女同学}
交集:
由属于集合A且属于集合B的元素组成的集合,称为A与B的交集(intersection set)
记作:A∩B (读作“A交B”)
即:
A∩B=
{x|x∈A且x∈B}
新华中学开运动会,设:
A={x|x是新华中学高一年级参加百米赛跑的同学}
B={x|x是新华中学高一年级参加跳高比赛的同学}
求A∩B
解:
A∩B=
{x|x是新华中学高一年级既参加百米赛跑又参加跳高比赛的同学}
设平面内直线l1上点的集合为L1,直线l2上点的集合为L2,试用集合的运算表示直线l1与l2的位置关系.
解:直线l1与l2在平面内有三种位置关系:
l1∩l2=
l1
l2
p
l1
l2
l1
l2
{点P}
l1∩l2=
Φ
l1∩l2=
l1=l2
已知A={x|x是等腰三角形},B={x|x是直角三角形},求A∩B,A∪B.
A∩B=
解:
{x|x是等腰直角三角形}
A∪B=
{x|x是等腰三角形或直角三角形}
A={x|x2-4x-5=0},B={x|x2=1},求A∩B,A∪B .
A∩B={x|x2-4x-5=0}∩{x|x2=1}
解:
={-1,5}∩{-1,1}
={-1}
A∪B=
{-1,5}∪{-1,1}
={-1,1,5}
集合A={x|-5≤x<1},B={x|x≤2},求A∩B,A∪B .
A∩B={x|-5≤x<1}∩{x|x≤2}
解:
={x|-5≤x<1}
A∪B={x|-5≤x<1}∪{x|x≤2}
={x|x≤2}
0
1
2
-5
-4
-1
-2
-3
x
0
1
2
-5
-4
-1
-2
-3
x
在研究集合时,经常遇到有关集合中元素个数的问题,我们把含有限个元素的集合A叫做有限集,用card表示有限集A中元素的个数.
例如:A={1,2,3},
那么card(A)=3
小王去采购一批物品,他采购了五类办公用品,三类电器,他一起采购了多少类物品?
办公用品类:电脑 办公桌 钢笔 纸 打印机
电器类 :彩电 洗衣机 电脑
card(A)=5
card(B)=3
card(A∩B)=1
card(A∪B)=card(A)+card(B)- card(A∩B)=5+3-1=7
他一起是采购了八类物品吗?
小王去采购一批物品,他采购了五类办公用品,三类电器,他一起采购了多少类物品?
假如:
办公用品类:电脑 办公桌 钢笔 纸 打印机
电器类 :彩电 洗衣机 电脑
观察下列两个集合,你能说出集合C与集合A、B之间的关系吗?
(1) A={1,3,5},B={2,4,6}
C={1,2,3,4,5,6}
(2) A={x|x是有理数},B={x|x是无理数}
C={x|x是实数}
并集:
由所有属于集合A或属于集合B的元素组成的集合,称为A与B的并集(union set).
记作:A∪B (读作“A并B”)
即:
A∪B=
{x|x∈A,或x∈B}
设A={3,5,7,8},B={4,6,8,9},求A∪B.
解:
A∪B={3,5,7,8}∪{4,6,8,9}
3 5
7
4 6
9
8
={3,4,5,6,7,8,9}
为什么8只出现了一次?
A={x|-1
1
2
3
4
-1
-2
-3
x
A={x|-1
0
1
2
3
4
-1
-2
-3
x
观察下列两个集合,你能说出集合C与集合A、B之间的关系吗?
(1)A={2,4,6,8,10},B={3,5,8,12}
C={8}
(2)A={我们班的女同学},B={我们班的所有同学}
C={我们班的女同学}
交集:
由属于集合A且属于集合B的元素组成的集合,称为A与B的交集(intersection set)
记作:A∩B (读作“A交B”)
即:
A∩B=
{x|x∈A且x∈B}
新华中学开运动会,设:
A={x|x是新华中学高一年级参加百米赛跑的同学}
B={x|x是新华中学高一年级参加跳高比赛的同学}
求A∩B
解:
A∩B=
{x|x是新华中学高一年级既参加百米赛跑又参加跳高比赛的同学}
设平面内直线l1上点的集合为L1,直线l2上点的集合为L2,试用集合的运算表示直线l1与l2的位置关系.
解:直线l1与l2在平面内有三种位置关系:
l1∩l2=
l1
l2
p
l1
l2
l1
l2
{点P}
l1∩l2=
Φ
l1∩l2=
l1=l2
已知A={x|x是等腰三角形},B={x|x是直角三角形},求A∩B,A∪B.
A∩B=
解:
{x|x是等腰直角三角形}
A∪B=
{x|x是等腰三角形或直角三角形}
A={x|x2-4x-5=0},B={x|x2=1},求A∩B,A∪B .
A∩B={x|x2-4x-5=0}∩{x|x2=1}
解:
={-1,5}∩{-1,1}
={-1}
A∪B=
{-1,5}∪{-1,1}
={-1,1,5}
集合A={x|-5≤x<1},B={x|x≤2},求A∩B,A∪B .
A∩B={x|-5≤x<1}∩{x|x≤2}
解:
={x|-5≤x<1}
A∪B={x|-5≤x<1}∪{x|x≤2}
={x|x≤2}
0
1
2
-5
-4
-1
-2
-3
x
0
1
2
-5
-4
-1
-2
-3
x
在研究集合时,经常遇到有关集合中元素个数的问题,我们把含有限个元素的集合A叫做有限集,用card表示有限集A中元素的个数.
例如:A={1,2,3},
那么card(A)=3
小王去采购一批物品,他采购了五类办公用品,三类电器,他一起采购了多少类物品?
办公用品类:电脑 办公桌 钢笔 纸 打印机
电器类 :彩电 洗衣机 电脑
card(A)=5
card(B)=3
card(A∩B)=1
card(A∪B)=card(A)+card(B)- card(A∩B)=5+3-1=7
