人教课标版高中数学必修1《函数的概念》基础训练(word版含解析)
文档属性
| 名称 | 人教课标版高中数学必修1《函数的概念》基础训练(word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 529.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-03 19:27:25 | ||
图片预览



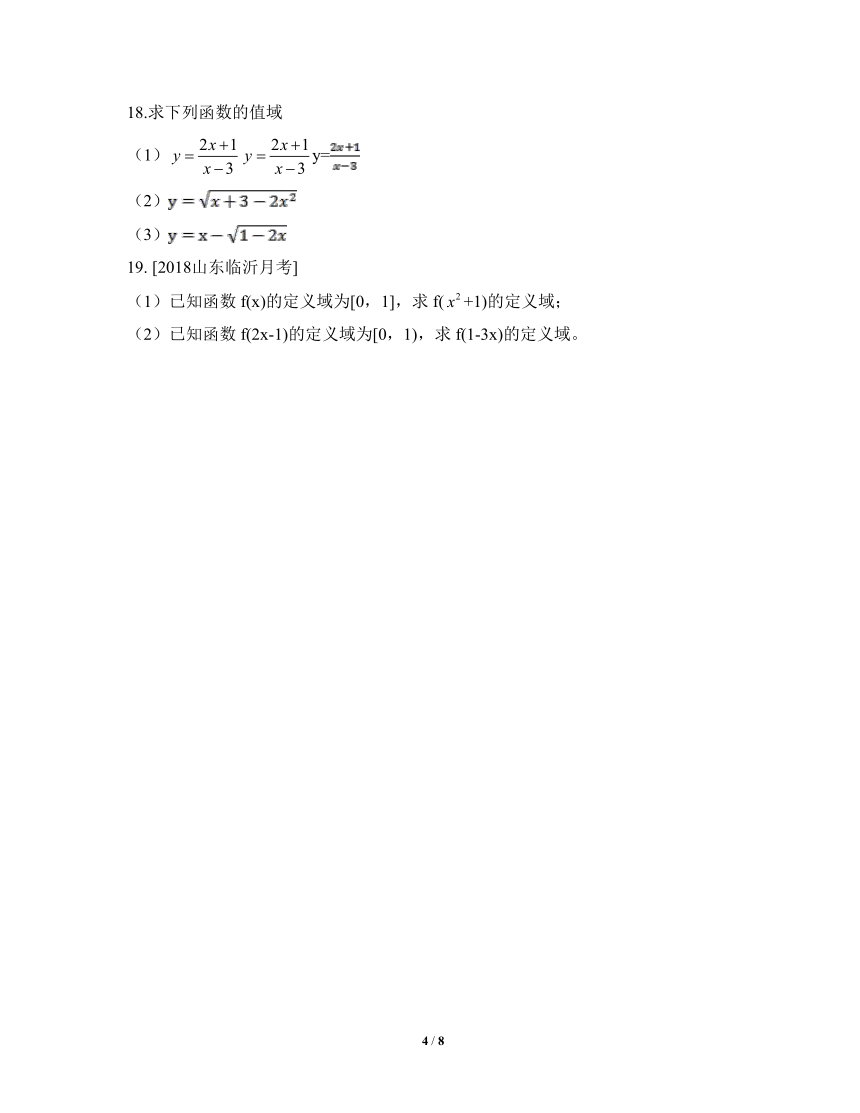
文档简介
《函数的概念》基础训练
一、选择题
1.[2017河北邯郸一中高中月考]下列对应是从集合M到集合N的函数的是()
A.M=R,N={x=R | x>0},f:x→|x|
B.M=N,N=N*,f:x→|x-1|
C.M=,N=R,f:
D.M=R,N={x=R| x0},f:
2.下列四个图中,不是以x为自变量的函数的图象是( )
3.区间(-3,2]用集合可表示为()
A. {-2,-1,0,1,2}
B. {x|-3C. {x|-3D. {x|-3≤x≤2}
4.[2017四川绵阳中学期末考试]已知函数f(x)=,则f(-2)=( )
A. -1
B. 0
C. 1
D. 2
5.若函数y=-3x的定义域为{-1,0,2,3}则其值域为()
A. {-2,0,4}
B. {-2,0,2,4}
C.
D. {y|0y≤3}
6.[2018江西南昌二中期中考试]下列函数中,值域为[1,+)的是()
A. y=
B. y=
C. y=
D. y=
7.[2018福建泉州五中期末考试]若函数y=f(x)的定义域是[-2,4],则函数g(x)=f(x)+f(-x)的定义域是( )
A. [-4,4]
B. [-2,2]
C. [-4,-2]
D. [2,4]
二、填空题
8.用区间表示下列集合:
(1){x| x1}=___________;
(2)=______________;
(3){x| x=1或2≤x≤8}=________________;
(4){x| x<-4或-19.函数f(x)=的值域是_____________.
10.若f(x)=,且f(a)=2,则a=_______.
11.[2018江苏苏州五中高一(上)月考]设函数f(n)=k(n),其中k是无理数m的小数点后的第n位数字,=3.141 592 653 589…,则f(f(f(10)))=__________.
12.[2018黑龙江大庆一中高一(上)月考]若函数f(x)满足对任意实数a,b都有f(a+b)=f(a)f(b)0,且f(1)=1,则___________ .
13.已知f(0)=1,f(n)=nf(n-1),nN*,则f(3)=_______.
三、解答题
14.[2018湖北武汉高一(上)月考]已知集合A={x|7-x0},集合B={x||x|-20},求AB,并用区间表示出来。
15.求下列函数的定义域
(1)
(2)
(3)
(4)
16.[2018安徽铜陵一中期末考试]已知函数的定义域为A,
的定义域为B.
(1)若BA,求实数a的取值范围;
(2)若AB,求实数a的取值范围.
17.已知f(x)=(xR,且x-1),g(x)=-1(xR).
(1)求f(2),g(3)的值;
(2)求f(g(3))的值及f(g(x)).
18.求下列函数的值域
(1)y=
(2)
(3)
19. [2018山东临沂月考]
(1)已知函数f(x)的定义域为[0,1],求f(+1)的定义域;
(2)已知函数f(2x-1)的定义域为[0,1),求f(1-3x)的定义域。
参考答案
1. 答案:C
解析:对于A,集合M中x=0时,|x|=0,但集合N中没0;对于B,集合M中x=1时,|x-1|=0,但集合N中没有0;对D,集合M中x为负数时,集合N中没有元素与之对应;分析知C对应是集合M到集合N的函数.
2. 答案:C
解析:根据函数定义,知对自变量x的任意一个值,都有唯一确定的实数(函数值)与之对应.显然选项A,B,D满足函数的定义,而选项C不满足.故选C.
3. 答案:C
解析:由区间和集合的关系,可得区间(-3,2]可表示为{x|-34. 答案:C
解析:由题意知(-2)=.故选C.
5. 答案:A
解析:依题意,当x=-1时,y=4;当x=0时,y=0;当x=2时,y=-2;当x=3时,y=0,所以函数y=-3x的值域为{-2,0,4}.
6. 答案:C
解析:因为y=,值域为[0,+),所以A不满足题意;
因为,值域为(-0,0)(0,+0),所以B不满足题意;
因为y=,值域为[1,+),所以C满足题意;因为y=,值域为(0,+),所以D不满足题意.故选C.
7. 答案:B
解析:由,得。
8. 答案:(1)[1,+);(2)(-,-1)[2,+);(3){1}[2,8]
(4)(-,-4)(-1,2]
解析:(1){x |x≥1}=[1,+).
(2){x|
(3).
(4){x |x<-4或-19. 答案:[2,11]
解析:由题意,得抛物线y=+2开口向上,对称轴是y轴,所以函数f(x)=+2在[-1,3]上的最小值为2,最大值为11,所以函数f(x)的值域是[2,11].
10. 答案:或2
解析:令=2,即2-5x+2=0,解得x=或x=2,故a的值为或2.
11. 答案:3
解析:依题意,得f(10)=5,f(f(10))=f(5)=9.f(9)=3,所以f(f(f(10)))=3.
12. 答案:2017
解析:由f(a+b)=f(a)f(b),令b=1,得f(a+1)=f(a)f(1).又f(1)=1,所以f(a+1)=f(a).又f(a)0,则f(a+1)/ f(a)=1.又a是任意实数,所以当a取1,2,3…,2017时,得
,所以
13. 答案:6
解析:令n=1,得f(1)=f(0)=1;令n=2,得f(2)=2f(1)=2;令n=3,得f(3)=3f(2)=6.
14. 答案:见解析
解析:因为A={x|7-x≥0}={x | x≤7},B={x|}={x | x±2|,所以AB={x | x<-2或-215. 答案:(1)(-,0);(2)[-2,1)(1,+);(3)[-2,-1)(-1,2];(4){5}
解析:(1)因为|x|-x0,即|x|(2)由所以该函数的定义域为[-2,1)(1,+).
(3)由所以该函数的定义域为[-2,-1)(-1,2].
(4)由,所以x=5,所以该函数的定义域为{5}.
16. 答案:(1){a |a≤3};(2){a |a≥3}
解析:(1)由题意知,A={x |x<3},B={x |x(2)若AB,则a≥3.实数a的取值范围是{a |a≥3}.
17. 答案:(1) ,8 ;(2)
解析:(1)因为,所以
因为g(x)=-1,所以g(3)=-1=8.
(2)依题意,知f(g(3))=f(8)==
18. 答案:(1)(- ,2)(2,+ );(2)[0, ] ;(3)(-, ] .
解析:(1)因为y=所以,y2
所以原函数的值域为.
(2)因为,
所以,所以原函数的值域为.
(3)设,则
得
因为,所以,即该函数的值域为
19. 答案:(1){x|x=0};(2)(0,].
解析:(1)因为函数f(x2+1)中的x2+1相当于函数f(x)中的x,
所以0≤+1≤1,即 -1≤≤0,所以x=0.故函数f(+1)的定义域为{x|x=0}.
(2)因为函数f(2x-1)的定义域为[0,1),即0≤x<1,所以-1≤2x-1<1,则f(x)的定义域为[-1,1),所以-1=1-3x<1,解得01 / 3
一、选择题
1.[2017河北邯郸一中高中月考]下列对应是从集合M到集合N的函数的是()
A.M=R,N={x=R | x>0},f:x→|x|
B.M=N,N=N*,f:x→|x-1|
C.M=,N=R,f:
D.M=R,N={x=R| x0},f:
2.下列四个图中,不是以x为自变量的函数的图象是( )
3.区间(-3,2]用集合可表示为()
A. {-2,-1,0,1,2}
B. {x|-3
4.[2017四川绵阳中学期末考试]已知函数f(x)=,则f(-2)=( )
A. -1
B. 0
C. 1
D. 2
5.若函数y=-3x的定义域为{-1,0,2,3}则其值域为()
A. {-2,0,4}
B. {-2,0,2,4}
C.
D. {y|0y≤3}
6.[2018江西南昌二中期中考试]下列函数中,值域为[1,+)的是()
A. y=
B. y=
C. y=
D. y=
7.[2018福建泉州五中期末考试]若函数y=f(x)的定义域是[-2,4],则函数g(x)=f(x)+f(-x)的定义域是( )
A. [-4,4]
B. [-2,2]
C. [-4,-2]
D. [2,4]
二、填空题
8.用区间表示下列集合:
(1){x| x1}=___________;
(2)=______________;
(3){x| x=1或2≤x≤8}=________________;
(4){x| x<-4或-1
10.若f(x)=,且f(a)=2,则a=_______.
11.[2018江苏苏州五中高一(上)月考]设函数f(n)=k(n),其中k是无理数m的小数点后的第n位数字,=3.141 592 653 589…,则f(f(f(10)))=__________.
12.[2018黑龙江大庆一中高一(上)月考]若函数f(x)满足对任意实数a,b都有f(a+b)=f(a)f(b)0,且f(1)=1,则___________ .
13.已知f(0)=1,f(n)=nf(n-1),nN*,则f(3)=_______.
三、解答题
14.[2018湖北武汉高一(上)月考]已知集合A={x|7-x0},集合B={x||x|-20},求AB,并用区间表示出来。
15.求下列函数的定义域
(1)
(2)
(3)
(4)
16.[2018安徽铜陵一中期末考试]已知函数的定义域为A,
的定义域为B.
(1)若BA,求实数a的取值范围;
(2)若AB,求实数a的取值范围.
17.已知f(x)=(xR,且x-1),g(x)=-1(xR).
(1)求f(2),g(3)的值;
(2)求f(g(3))的值及f(g(x)).
18.求下列函数的值域
(1)y=
(2)
(3)
19. [2018山东临沂月考]
(1)已知函数f(x)的定义域为[0,1],求f(+1)的定义域;
(2)已知函数f(2x-1)的定义域为[0,1),求f(1-3x)的定义域。
参考答案
1. 答案:C
解析:对于A,集合M中x=0时,|x|=0,但集合N中没0;对于B,集合M中x=1时,|x-1|=0,但集合N中没有0;对D,集合M中x为负数时,集合N中没有元素与之对应;分析知C对应是集合M到集合N的函数.
2. 答案:C
解析:根据函数定义,知对自变量x的任意一个值,都有唯一确定的实数(函数值)与之对应.显然选项A,B,D满足函数的定义,而选项C不满足.故选C.
3. 答案:C
解析:由区间和集合的关系,可得区间(-3,2]可表示为{x|-3
解析:由题意知(-2)=.故选C.
5. 答案:A
解析:依题意,当x=-1时,y=4;当x=0时,y=0;当x=2时,y=-2;当x=3时,y=0,所以函数y=-3x的值域为{-2,0,4}.
6. 答案:C
解析:因为y=,值域为[0,+),所以A不满足题意;
因为,值域为(-0,0)(0,+0),所以B不满足题意;
因为y=,值域为[1,+),所以C满足题意;因为y=,值域为(0,+),所以D不满足题意.故选C.
7. 答案:B
解析:由,得。
8. 答案:(1)[1,+);(2)(-,-1)[2,+);(3){1}[2,8]
(4)(-,-4)(-1,2]
解析:(1){x |x≥1}=[1,+).
(2){x|
(3).
(4){x |x<-4或-1
解析:由题意,得抛物线y=+2开口向上,对称轴是y轴,所以函数f(x)=+2在[-1,3]上的最小值为2,最大值为11,所以函数f(x)的值域是[2,11].
10. 答案:或2
解析:令=2,即2-5x+2=0,解得x=或x=2,故a的值为或2.
11. 答案:3
解析:依题意,得f(10)=5,f(f(10))=f(5)=9.f(9)=3,所以f(f(f(10)))=3.
12. 答案:2017
解析:由f(a+b)=f(a)f(b),令b=1,得f(a+1)=f(a)f(1).又f(1)=1,所以f(a+1)=f(a).又f(a)0,则f(a+1)/ f(a)=1.又a是任意实数,所以当a取1,2,3…,2017时,得
,所以
13. 答案:6
解析:令n=1,得f(1)=f(0)=1;令n=2,得f(2)=2f(1)=2;令n=3,得f(3)=3f(2)=6.
14. 答案:见解析
解析:因为A={x|7-x≥0}={x | x≤7},B={x|}={x | x±2|,所以AB={x | x<-2或-2
解析:(1)因为|x|-x0,即|x|
(3)由所以该函数的定义域为[-2,-1)(-1,2].
(4)由,所以x=5,所以该函数的定义域为{5}.
16. 答案:(1){a |a≤3};(2){a |a≥3}
解析:(1)由题意知,A={x |x<3},B={x |x
17. 答案:(1) ,8 ;(2)
解析:(1)因为,所以
因为g(x)=-1,所以g(3)=-1=8.
(2)依题意,知f(g(3))=f(8)==
18. 答案:(1)(- ,2)(2,+ );(2)[0, ] ;(3)(-, ] .
解析:(1)因为y=所以,y2
所以原函数的值域为.
(2)因为,
所以,所以原函数的值域为.
(3)设,则
得
因为,所以,即该函数的值域为
19. 答案:(1){x|x=0};(2)(0,].
解析:(1)因为函数f(x2+1)中的x2+1相当于函数f(x)中的x,
所以0≤+1≤1,即 -1≤≤0,所以x=0.故函数f(+1)的定义域为{x|x=0}.
(2)因为函数f(2x-1)的定义域为[0,1),即0≤x<1,所以-1≤2x-1<1,则f(x)的定义域为[-1,1),所以-1=1-3x<1,解得0
