数阵问题(课件)-2021-2022学年数学五年级上册(共20张PPT)人教版
文档属性
| 名称 | 数阵问题(课件)-2021-2022学年数学五年级上册(共20张PPT)人教版 |  | |
| 格式 | zip | ||
| 文件大小 | 982.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-01 12:46:42 | ||
图片预览





文档简介
(共20张PPT)
数阵问题
引入
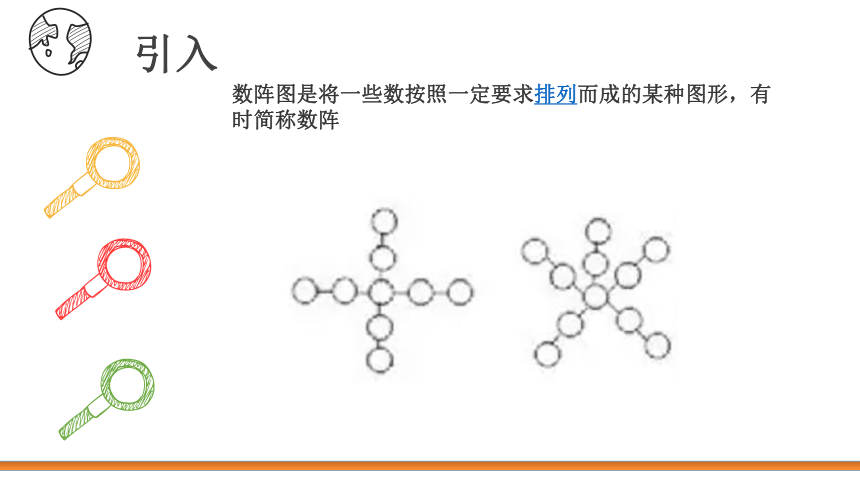
数阵图是将一些数按照一定要求排列而成的某种图形,有时简称数阵
大王,求求你放了我们吧!
放了你们,可以!先过了我设置的“数阵”关,再说!
4
用1、2、3、4、5填入下面方框,使每三个数之和等于8 。
4
5
3
2
1
解析:
求和:1+2+3+4+5=15。
8+8=16。
作差:16-15=1
(中间方格里的数字被重复使用一次,这个重复使用的数字是16-15=1,所以中间的方格应填数字1)。
配对(2和5、3和4)
第一关
例1
5
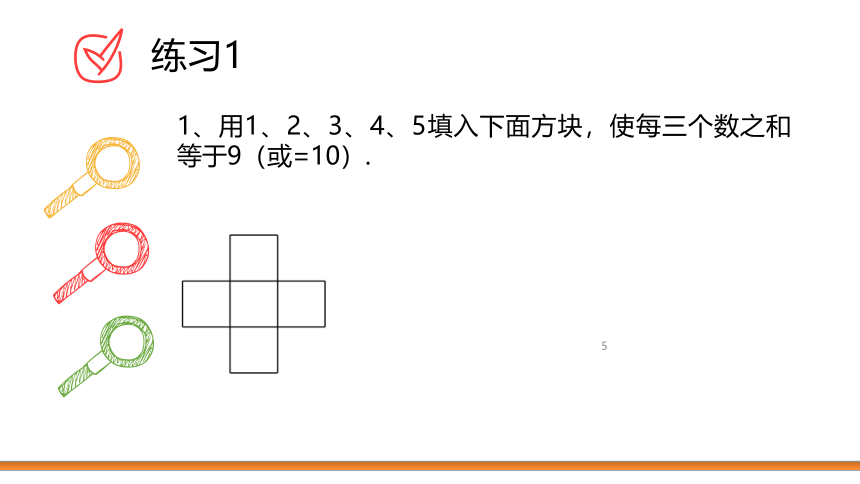
1、用1、2、3、4、5填入下面方块,使每三个数之和等于9(或=10).
练习1
6
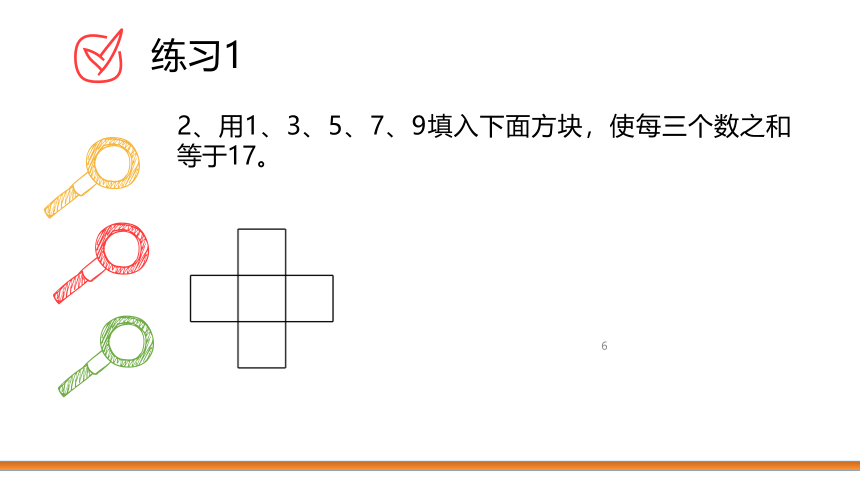
2、用1、3、5、7、9填入下面方块,使每三个数之和等于17。
练习1
7
用1、2、3、4、5、6、7填入下面圆内,使每条直线上三数之和等于10。
第一关
例2
8
用1、2、3、4、5、6、7填入下面圆内,使每条直线上三数之和等于10。
第二关
例2
解析:
求和:1+2+3+4+5+6+7=28
10×3=30
作差:30-28=2
中间圆圈里的数字被重复用了两次,所以中间的数字是:2÷2=1
配对:一大配一小。
7
2
1
4
5
6
3
9
练习2
9
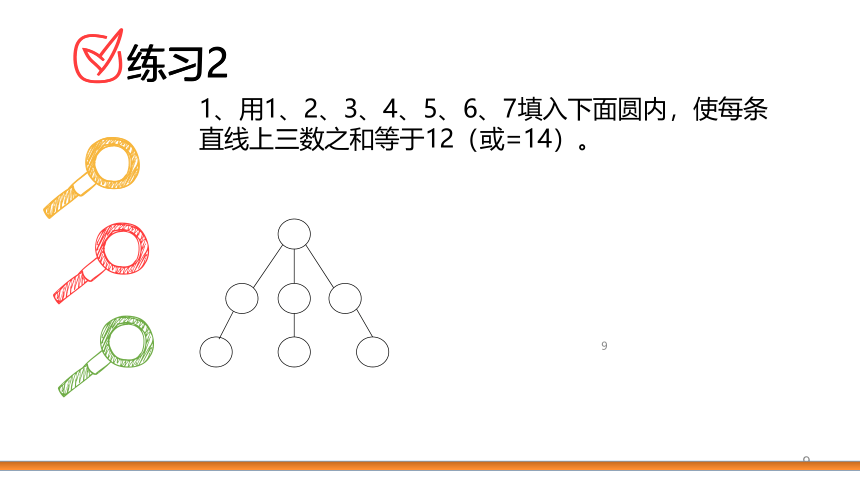
1、用1、2、3、4、5、6、7填入下面圆内,使每条直线上三数之和等于12(或=14)。
练习2
10
10
2、用1、3、5、7、9、11、13填入下面圆内,使每条直线上三个数之和等于21。
练习2
11
(1)用1、2、3、4、5、6填入下面圈内,使三角形每条边上三
个数之和等于9。
第三关
例3
12
(1)用1、2、3、4、5、6填入下面圈内,使三角形每条边上三个数之和等于9。
解析:1+2+3+4+5+6=21。
若使三角形每条边上三个数之和等于9,则三条边上所有数字之和为9×3=27。
这样三角形三个顶点的数字都重复算了一次,
所以三个顶点的数字之和为27-21=6。
把6分为1+2+3,
所以三个顶点的数字分别为1,2,3。
剩下三个数字的填法应根据“三角形每条边上三个数之和等于9”进行填写。
例3
13
(1)用1、2、3、4、5、6填入下面圈内,使三角形每条边上三
个数之和等于9。
解析:
1.求和
1+2+3+4+5+6=21
9×3=27
2.作差(三数之和)
27-21=6
3.拆数
6=1+2+3
配对:两小配一大,两大配一小。
例3
辐射型数阵图 关键点:重叠数
如果所填的数是连续数,可以尝试重叠数为最大的、最小的、中间数
其余的:大手拉小手
总结
15
将1、2、3、4、5、6、7、8这八个数分别填入下图中的○内,使每一个圆周上的五个数之和都等于21。
第四关
例4
16
将1、2、3、4、5、6、7、8这八个数分别填入下图中的○内,使每一个圆周上的五个数之和都等于21。
解析:1+2+3+4+5+6+7+8=36。
若每一个圆周上的五个数之和都等于21,
那么这两个圆周上所有数字之和应该为21×2=42。
中间两个圆圈上的两个数字被重复用了一次,
被重复的两个数字之和应为42-36=6。
6可以被分成4与2的和,
所以中间两个数为4,2。
剩下的数字根据题目要求填写即可。
填法如左图(答案不唯一)。
例4
17
将1、2、3、4、5、6、7、8这八个数分别填入下图中的○内,使每一个圆周上的五个数之和都等于21。
解析:
求和: 1+2+3+4+5+6+7+8=36。
21×2=42。
作差:42-36=6。
拆数:6=2+4,
所以中间两个数为4,2。
例4
18
1.将1、2、3、4、5、6、7、8这八个数分别填入下图中的○内,使每一个圆圈上的五个数的和都等于22。
练习4
19
2、用1、2、3、4、5、6、7填入下面圈内,使每个四边形之和等于15。(等于16或17呢?)
练习4
数阵图,关键点是找出重叠数
1、辐射型——
连续的数:尝试法:头、尾、中间数;其余大手拉小手 不连续的数:拆数法
2、封闭型—— 拆数法
总结
数阵问题
引入
数阵图是将一些数按照一定要求排列而成的某种图形,有时简称数阵
大王,求求你放了我们吧!
放了你们,可以!先过了我设置的“数阵”关,再说!
4
用1、2、3、4、5填入下面方框,使每三个数之和等于8 。
4
5
3
2
1
解析:
求和:1+2+3+4+5=15。
8+8=16。
作差:16-15=1
(中间方格里的数字被重复使用一次,这个重复使用的数字是16-15=1,所以中间的方格应填数字1)。
配对(2和5、3和4)
第一关
例1
5
1、用1、2、3、4、5填入下面方块,使每三个数之和等于9(或=10).
练习1
6
2、用1、3、5、7、9填入下面方块,使每三个数之和等于17。
练习1
7
用1、2、3、4、5、6、7填入下面圆内,使每条直线上三数之和等于10。
第一关
例2
8
用1、2、3、4、5、6、7填入下面圆内,使每条直线上三数之和等于10。
第二关
例2
解析:
求和:1+2+3+4+5+6+7=28
10×3=30
作差:30-28=2
中间圆圈里的数字被重复用了两次,所以中间的数字是:2÷2=1
配对:一大配一小。
7
2
1
4
5
6
3
9
练习2
9
1、用1、2、3、4、5、6、7填入下面圆内,使每条直线上三数之和等于12(或=14)。
练习2
10
10
2、用1、3、5、7、9、11、13填入下面圆内,使每条直线上三个数之和等于21。
练习2
11
(1)用1、2、3、4、5、6填入下面圈内,使三角形每条边上三
个数之和等于9。
第三关
例3
12
(1)用1、2、3、4、5、6填入下面圈内,使三角形每条边上三个数之和等于9。
解析:1+2+3+4+5+6=21。
若使三角形每条边上三个数之和等于9,则三条边上所有数字之和为9×3=27。
这样三角形三个顶点的数字都重复算了一次,
所以三个顶点的数字之和为27-21=6。
把6分为1+2+3,
所以三个顶点的数字分别为1,2,3。
剩下三个数字的填法应根据“三角形每条边上三个数之和等于9”进行填写。
例3
13
(1)用1、2、3、4、5、6填入下面圈内,使三角形每条边上三
个数之和等于9。
解析:
1.求和
1+2+3+4+5+6=21
9×3=27
2.作差(三数之和)
27-21=6
3.拆数
6=1+2+3
配对:两小配一大,两大配一小。
例3
辐射型数阵图 关键点:重叠数
如果所填的数是连续数,可以尝试重叠数为最大的、最小的、中间数
其余的:大手拉小手
总结
15
将1、2、3、4、5、6、7、8这八个数分别填入下图中的○内,使每一个圆周上的五个数之和都等于21。
第四关
例4
16
将1、2、3、4、5、6、7、8这八个数分别填入下图中的○内,使每一个圆周上的五个数之和都等于21。
解析:1+2+3+4+5+6+7+8=36。
若每一个圆周上的五个数之和都等于21,
那么这两个圆周上所有数字之和应该为21×2=42。
中间两个圆圈上的两个数字被重复用了一次,
被重复的两个数字之和应为42-36=6。
6可以被分成4与2的和,
所以中间两个数为4,2。
剩下的数字根据题目要求填写即可。
填法如左图(答案不唯一)。
例4
17
将1、2、3、4、5、6、7、8这八个数分别填入下图中的○内,使每一个圆周上的五个数之和都等于21。
解析:
求和: 1+2+3+4+5+6+7+8=36。
21×2=42。
作差:42-36=6。
拆数:6=2+4,
所以中间两个数为4,2。
例4
18
1.将1、2、3、4、5、6、7、8这八个数分别填入下图中的○内,使每一个圆圈上的五个数的和都等于22。
练习4
19
2、用1、2、3、4、5、6、7填入下面圈内,使每个四边形之和等于15。(等于16或17呢?)
练习4
数阵图,关键点是找出重叠数
1、辐射型——
连续的数:尝试法:头、尾、中间数;其余大手拉小手 不连续的数:拆数法
2、封闭型—— 拆数法
总结
