青岛版初中数学七年级上册 1.4 线段的比较与作法课件(共18张PPT)
文档属性
| 名称 | 青岛版初中数学七年级上册 1.4 线段的比较与作法课件(共18张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 439.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-01 11:48:57 | ||
图片预览

文档简介
(共18张PPT)
线段的比较与作法
问题(1):小狗、小猫为什么都选择直的路?
想一想:
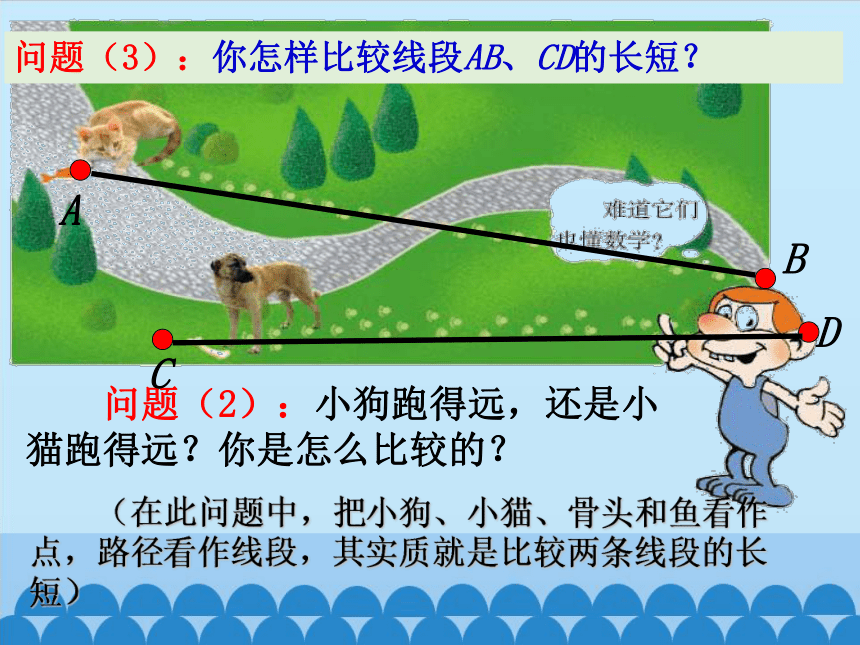
(在此问题中,把小狗、小猫、骨头和鱼看作点,路径看作线段,其实质就是比较两条线段的长短)
问题(2):小狗跑得远,还是小猫跑得远?你是怎么比较的?
B
D
A
C
问题(3):你怎样比较线段AB、CD的长短?
D
C
B
A
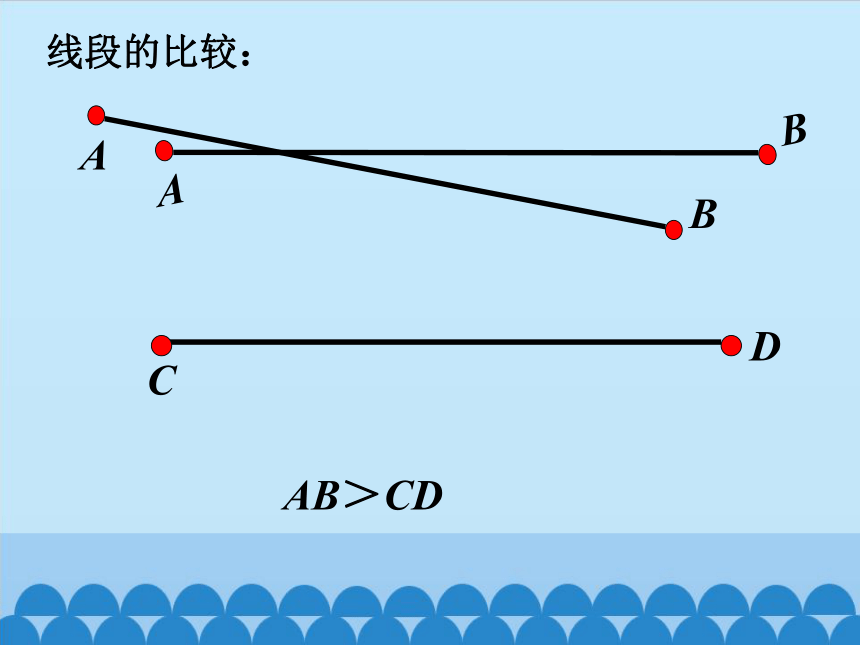
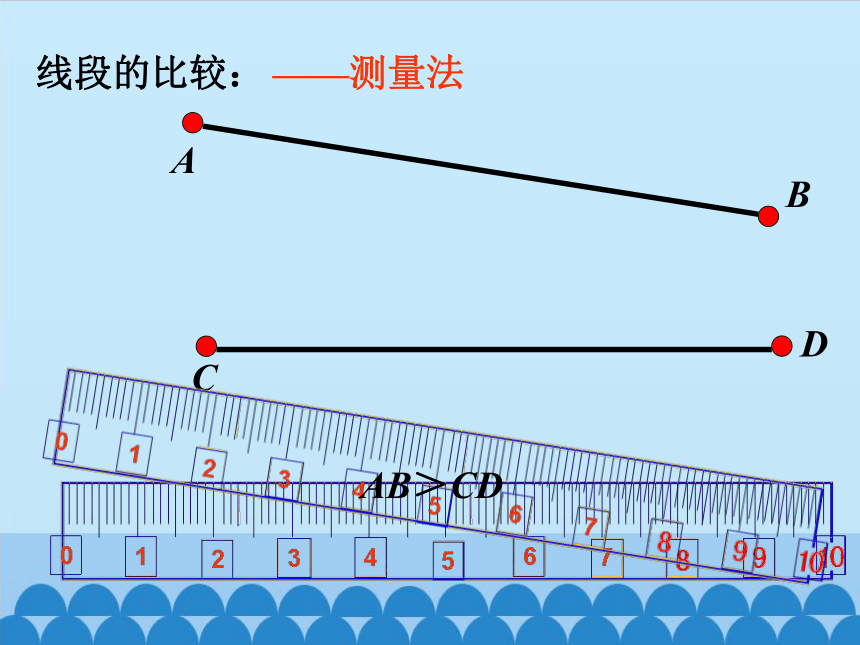
线段的比较:
B
A
AB>CD
A
B
A
B
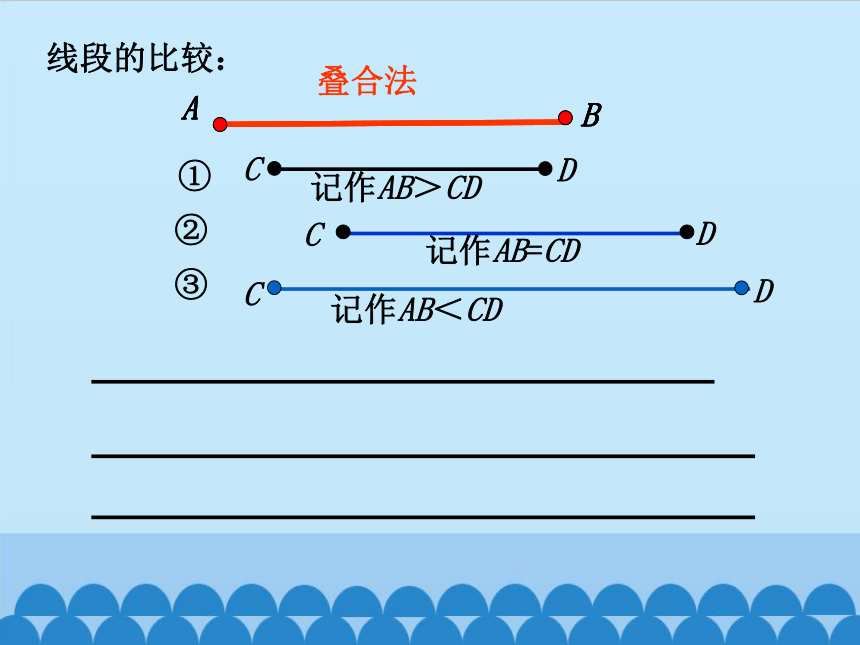
线段的比较:
A
B
叠合法
①
②
③
C
D
C
D
C
D
记作AB>CD
记作AB=CD
记作AB<CD
D
C
B
A
线段的比较:
——测量法
AB>CD
A·
·B
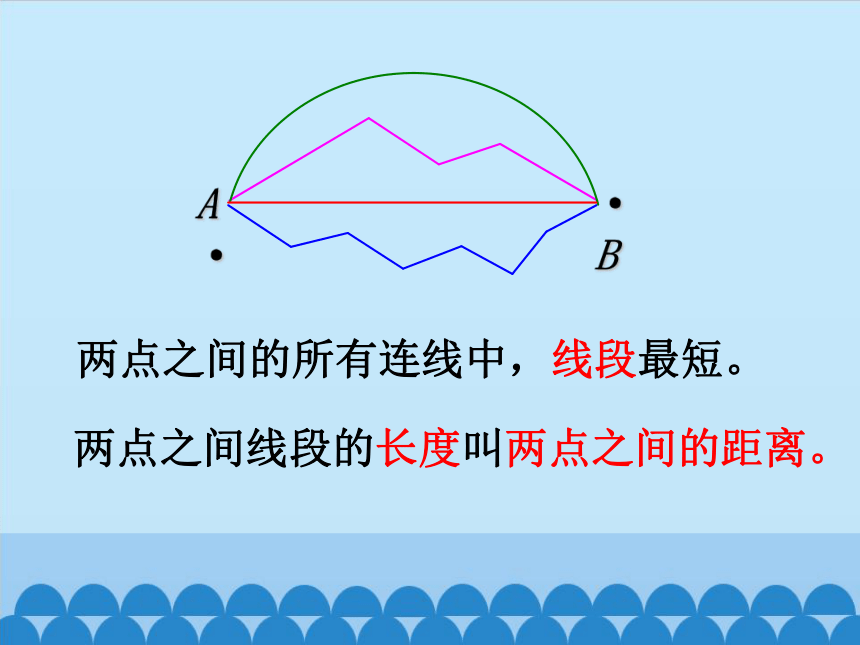
两点之间的所有连线中,线段最短。
两点之间线段的长度叫两点之间的距离。
认识测量仪器,如:游标卡尺。
1.比较两条线段AB与CD的长短,结果可能有几种情形?画图说明。
解:三种情形
AB
CD
AB
CD
AB
CD
2.下列叙述正确吗?为什么?
(1)线段AB叫做A,B两点间的距离;
(2)经过点A和点B的直线的长度叫做A,B两点间的距离。
√
×
3.如图,MN表示一条河流,A,B两点表示两个村庄,它们分别在河流两旁。现准备在河上建一座桥,使两村人们来往最便捷。小亮想,如果能在MN上找到一点D,使D点与A,B两点的距离相等,那么,在D点建桥最合理。你认为他的想法正确吗?为什么?
解:不正确,因为D点与A点和B点的距离之和不是A、B两点间的最短距离。
a
已知线段a,请用圆规、直尺作一条线段AC,使AC=a。
活动2
1.用直尺作一条射线AB。
2.用圆规量出已知线段a的长度。
3.在射线AB上,以点A为圆心,以a为半径画弧,交射线AB 与点C,即截取AC=a。
A
B
C
那么线段AC就是所作线段。
表达式:如果点M是线段AB的中点,那么AM=BM= AB。
已知线段AB,在线段AB上找一点M,使点M平分线段AB 。
A
B
M
点M把线段AB分成相等的两条线段AM与BM,点M叫做线段AB的中点。
活动3
反过来:如果 AM=BM= AB ,那么点M是线段AB的中点。
(2) 在直线上顺次取出A、B、C三点使AB=4cm,BC=3cm,如果O是线段AC的中点,求线段OB的长度?
解:因为AB=4cm BC=3cm,
所以AC=AB+BC=7cm,
因为点O是线段AC的中点,
所以OC= AC =3.5cm,
所以OB=OC-BC =3.5-3 =0.5(cm)。
答:线段OB的长为0.5cm。
A
C
1.已知线段a,用直尺和圆规作一条线段AB,使它的长度等于2a。
①作射线AC;
②取AB =2a。
解:作法:
a
∴线段AB为所求。
B
2.如图,D为线段CB的中点,AD=8厘米,AB=10厘米,求CB的长度。
。
。
。
。
A
C
D
B
∵ 点D是线段CB的中点,
∵ AD=8厘米,AB=10厘米,
∴ BD=AB-AD =2厘米。
∴ CD =BD。
∴ CB=2BD=4厘米。
拓展:如图是一个四边形,在各边上任意取一点,并顺次连接它们,想一想你得到的图形周长与原四边形周长哪一个大?为什么?如果是一个五边形呢?六边形呢?
谈谈这节课你的收获?
1.线段的基本性质:
2.两点之间的距离:
3.线段的两种比较方法:
4.线段的中点的概念及表示方法。
两点之间线段最短。
两点之间线段的长度。
叠合法和测量法。
谢 谢
线段的比较与作法
问题(1):小狗、小猫为什么都选择直的路?
想一想:
(在此问题中,把小狗、小猫、骨头和鱼看作点,路径看作线段,其实质就是比较两条线段的长短)
问题(2):小狗跑得远,还是小猫跑得远?你是怎么比较的?
B
D
A
C
问题(3):你怎样比较线段AB、CD的长短?
D
C
B
A
线段的比较:
B
A
AB>CD
A
B
A
B
线段的比较:
A
B
叠合法
①
②
③
C
D
C
D
C
D
记作AB>CD
记作AB=CD
记作AB<CD
D
C
B
A
线段的比较:
——测量法
AB>CD
A·
·B
两点之间的所有连线中,线段最短。
两点之间线段的长度叫两点之间的距离。
认识测量仪器,如:游标卡尺。
1.比较两条线段AB与CD的长短,结果可能有几种情形?画图说明。
解:三种情形
AB
CD
AB
CD
AB
CD
2.下列叙述正确吗?为什么?
(1)线段AB叫做A,B两点间的距离;
(2)经过点A和点B的直线的长度叫做A,B两点间的距离。
√
×
3.如图,MN表示一条河流,A,B两点表示两个村庄,它们分别在河流两旁。现准备在河上建一座桥,使两村人们来往最便捷。小亮想,如果能在MN上找到一点D,使D点与A,B两点的距离相等,那么,在D点建桥最合理。你认为他的想法正确吗?为什么?
解:不正确,因为D点与A点和B点的距离之和不是A、B两点间的最短距离。
a
已知线段a,请用圆规、直尺作一条线段AC,使AC=a。
活动2
1.用直尺作一条射线AB。
2.用圆规量出已知线段a的长度。
3.在射线AB上,以点A为圆心,以a为半径画弧,交射线AB 与点C,即截取AC=a。
A
B
C
那么线段AC就是所作线段。
表达式:如果点M是线段AB的中点,那么AM=BM= AB。
已知线段AB,在线段AB上找一点M,使点M平分线段AB 。
A
B
M
点M把线段AB分成相等的两条线段AM与BM,点M叫做线段AB的中点。
活动3
反过来:如果 AM=BM= AB ,那么点M是线段AB的中点。
(2) 在直线上顺次取出A、B、C三点使AB=4cm,BC=3cm,如果O是线段AC的中点,求线段OB的长度?
解:因为AB=4cm BC=3cm,
所以AC=AB+BC=7cm,
因为点O是线段AC的中点,
所以OC= AC =3.5cm,
所以OB=OC-BC =3.5-3 =0.5(cm)。
答:线段OB的长为0.5cm。
A
C
1.已知线段a,用直尺和圆规作一条线段AB,使它的长度等于2a。
①作射线AC;
②取AB =2a。
解:作法:
a
∴线段AB为所求。
B
2.如图,D为线段CB的中点,AD=8厘米,AB=10厘米,求CB的长度。
。
。
。
。
A
C
D
B
∵ 点D是线段CB的中点,
∵ AD=8厘米,AB=10厘米,
∴ BD=AB-AD =2厘米。
∴ CD =BD。
∴ CB=2BD=4厘米。
拓展:如图是一个四边形,在各边上任意取一点,并顺次连接它们,想一想你得到的图形周长与原四边形周长哪一个大?为什么?如果是一个五边形呢?六边形呢?
谈谈这节课你的收获?
1.线段的基本性质:
2.两点之间的距离:
3.线段的两种比较方法:
4.线段的中点的概念及表示方法。
两点之间线段最短。
两点之间线段的长度。
叠合法和测量法。
谢 谢
同课章节目录
- 第1章 基本的几何图形
- 1.1 我们身边的图形世界
- 1.2 几何图形
- 1.3 线段、射线和直线
- 1.4 线段的比较与作法
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数与绝对值
- 第3章 有理数的运算
- 3.1 有理数的加法与减法
- 3.2 有理数的乘法与除法
- 3.3 有理数的乘方
- 3.4 有理数的混合运算
- 3.5 利用计算器进行有理数的计算
- 第4章 数据的收集整理与描述
- 4.1 普查和抽样调查
- 4.2 简单随机抽样
- 4.3 数据的整理
- 4.4 扇形统计图
- 第5章 代数式与函数的初步认识
- 5.1 用字母表示数
- 5.2 代数式
- 5.3 代数式的值
- 5.4 生活中的常量与变量
- 5.5 函数的初步认识
- 第6章 整式的加减
- 6.1 单项式与多项式
- 6.2 同类项
- 6.3 去括号
- 6.4 整式的加减
- 第7章 一元一次方程
- 7.1 等式的基本性质
- 7.2 一元一次方程
- 7.3 一元一次方程的解法
- 7.4 一元一次方程的应用
