华东师大版数学九年级上册 25.2.2 频率与概率课件(共12张PPT)
文档属性
| 名称 | 华东师大版数学九年级上册 25.2.2 频率与概率课件(共12张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 557.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-02 14:43:26 | ||
图片预览




文档简介
(共12张PPT)
你是“玩家”吗
例题欣赏
例1 “石头、剪刀、布”是广为流传的游戏,游戏时甲乙双方每次做“石头”、“剪刀”、“布”三种手势中的一种,规定“石头”胜“剪刀”, “剪刀”胜“布”,“布”胜“石头”,同种手势不分胜负须继续比赛,假定甲乙两人每次都是等可能地做这三种手势,那么一次比赛时两人做同种手势(即不分胜负)的概率是多少?请先用树状图的方法解决,再用重复实验的方法,计算平均多少次中有一次会出现不分胜负的情况,比较以上两个结果,看能否互相验证。
做一做
“悟”的功效
小明去参加夏令营,带有2顶帽子,一顶是黄色的,一顶是紫色的,另外还带有黄色、白色、紫色上衣各一件,问随意拿出一件上衣和一顶帽子,恰好都是紫色的概率是多少?
驶向胜利的彼岸
学以致用
做一做
“配紫色”游戏
小颖为学校联欢会设计了一个“配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分成相等的几个扇形.
游戏规则是:游戏者同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,那么他就赢了,因为红色和蓝色在一起配成了紫色.
(1)利用树状图或列表的方法表示游戏者所有可能出现的结果.
(2)游戏者获胜的概率是多少
红
白
黄
蓝
绿
A盘
B盘
是“玩家”就玩出水平
1200
红
红
蓝
蓝
行家看“门道”
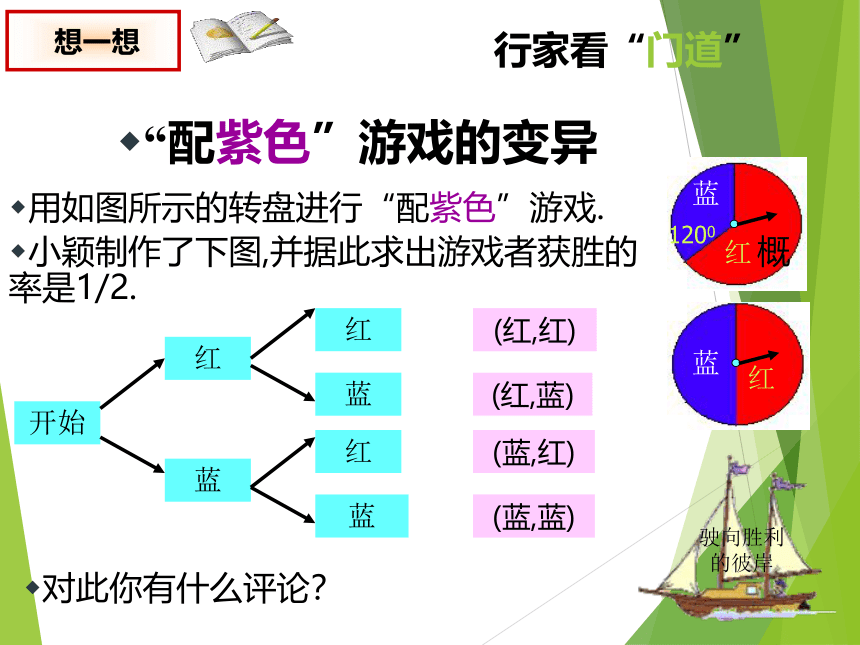
用如图所示的转盘进行“配紫色”游戏.
小颖制作了下图,并据此求出游戏者获胜的 概率是1/2.
驶向胜利的彼岸
“配紫色”游戏的变异
对此你有什么评论?
开始
红
蓝
红
蓝
红
蓝
(红,红)
(红,蓝)
(蓝,红)
(蓝,蓝)
想一想
行家看“门道”
想一想
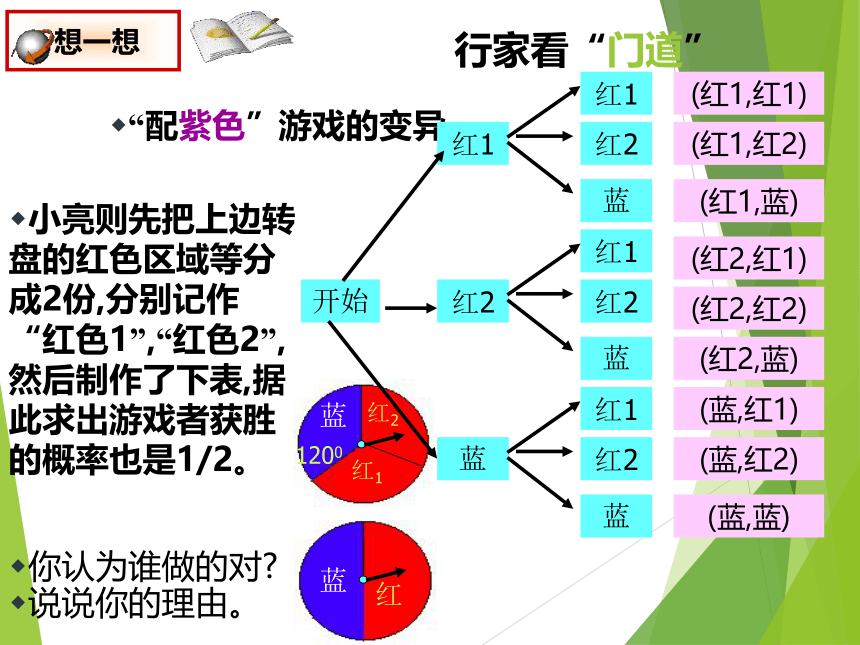
“配紫色”游戏的变异
小亮则先把上边转盘的红色区域等分成2份,分别记作“红色1”,“红色2”,然后制作了下表,据此求出游戏者获胜的概率也是1/2。
1200
红1
红
蓝
蓝
红2
你认为谁做的对
说说你的理由。
红1
红1
红2
蓝
红2
红1
红2
蓝
蓝
红1
红2
蓝
开始
(红1,红1)
(红1,红2)
(红1,蓝)
(红2,红1)
(红2,红2)
(红2,蓝)
(蓝,红1)
(蓝,红2)
(蓝,蓝)
真知灼见源于实践
议一议
由“配紫色”游戏的变异想到的
驶向胜利的彼岸
1200
红1
红
蓝
蓝
红2
小颖的做法不正确.因为上面的转盘中红色部分和蓝色部分的面积不相同,因而指针落在这两个区域的可能性不同.
小亮的做法是解决这类问题的一种常用方法.
1200
红
红
蓝
蓝
用树状图和列表的方法求概率时应注意些什么
用树状图和列表的方法求概率时应注意各种结果出现的可能性务必相同。
是“玩家”就玩出水平
如图,袋中装有两个完全相同的球,分别标有数字“1”和“2”.小明设计了一个游戏:游戏者每次从袋中随机摸出一个球,并自由转动图中的转盘(转盘被分成相等的三个扇形).
游戏规则是:
如果所摸球上的数字与转盘转出的数字之和为2,那么游戏者获胜.求游戏者获胜的概率.
驶向胜利的彼岸
用心领“悟”
1
2
3
做一做
是“玩家”就玩出水平
驶向胜利的彼岸
做一做
准备两组相同的牌,每组两张,两张牌面的数字分别是1和2。从两组牌中各摸出一张,则两张牌面数字之和可能有哪些值?
想一想,摸到两张牌的牌面数字之和为2的概率是几?为3、为4呢?
用实际行动证明我能行
知识的升华
拓 展
《史记》中有这样一个故事:有一天,喜欢赛马的齐王要田忌和他赛马,规定每个人从自己的上、中、下三等马中各选一匹来赛。当时,齐王的每一等次的马比田忌同样等次的马都要强。而双方的上等马比中等马强,中等马比下等马强。齐王的马出场是固定的,先后分别为上等马、中等马、下等马,经过孙膑的出谋划策,最终田忌神奇式的赢了,问田忌的出马顺序如何?用你所学的知识加以说明田忌战略的优越性。
大家听过田忌赛马的故事吗?
回味无穷
某一事件发生的可能性大小的这个数,可表示为概率。
利用树状图或表格可以清晰地表示出某个事件发生的所有可能出现的结果;
从而较方便地求出某些事件发生的概率.
小 结
2、本节课你学到了什么?
1、在游戏活动的过程中,你有什么感受?
结束寄语
询问者智之本,思虑者智之道也.
下课了!
你是“玩家”吗
例题欣赏
例1 “石头、剪刀、布”是广为流传的游戏,游戏时甲乙双方每次做“石头”、“剪刀”、“布”三种手势中的一种,规定“石头”胜“剪刀”, “剪刀”胜“布”,“布”胜“石头”,同种手势不分胜负须继续比赛,假定甲乙两人每次都是等可能地做这三种手势,那么一次比赛时两人做同种手势(即不分胜负)的概率是多少?请先用树状图的方法解决,再用重复实验的方法,计算平均多少次中有一次会出现不分胜负的情况,比较以上两个结果,看能否互相验证。
做一做
“悟”的功效
小明去参加夏令营,带有2顶帽子,一顶是黄色的,一顶是紫色的,另外还带有黄色、白色、紫色上衣各一件,问随意拿出一件上衣和一顶帽子,恰好都是紫色的概率是多少?
驶向胜利的彼岸
学以致用
做一做
“配紫色”游戏
小颖为学校联欢会设计了一个“配紫色”游戏:下面是两个可以自由转动的转盘,每个转盘被分成相等的几个扇形.
游戏规则是:游戏者同时转动两个转盘,如果转盘A转出了红色,转盘B转出了蓝色,那么他就赢了,因为红色和蓝色在一起配成了紫色.
(1)利用树状图或列表的方法表示游戏者所有可能出现的结果.
(2)游戏者获胜的概率是多少
红
白
黄
蓝
绿
A盘
B盘
是“玩家”就玩出水平
1200
红
红
蓝
蓝
行家看“门道”
用如图所示的转盘进行“配紫色”游戏.
小颖制作了下图,并据此求出游戏者获胜的 概率是1/2.
驶向胜利的彼岸
“配紫色”游戏的变异
对此你有什么评论?
开始
红
蓝
红
蓝
红
蓝
(红,红)
(红,蓝)
(蓝,红)
(蓝,蓝)
想一想
行家看“门道”
想一想
“配紫色”游戏的变异
小亮则先把上边转盘的红色区域等分成2份,分别记作“红色1”,“红色2”,然后制作了下表,据此求出游戏者获胜的概率也是1/2。
1200
红1
红
蓝
蓝
红2
你认为谁做的对
说说你的理由。
红1
红1
红2
蓝
红2
红1
红2
蓝
蓝
红1
红2
蓝
开始
(红1,红1)
(红1,红2)
(红1,蓝)
(红2,红1)
(红2,红2)
(红2,蓝)
(蓝,红1)
(蓝,红2)
(蓝,蓝)
真知灼见源于实践
议一议
由“配紫色”游戏的变异想到的
驶向胜利的彼岸
1200
红1
红
蓝
蓝
红2
小颖的做法不正确.因为上面的转盘中红色部分和蓝色部分的面积不相同,因而指针落在这两个区域的可能性不同.
小亮的做法是解决这类问题的一种常用方法.
1200
红
红
蓝
蓝
用树状图和列表的方法求概率时应注意些什么
用树状图和列表的方法求概率时应注意各种结果出现的可能性务必相同。
是“玩家”就玩出水平
如图,袋中装有两个完全相同的球,分别标有数字“1”和“2”.小明设计了一个游戏:游戏者每次从袋中随机摸出一个球,并自由转动图中的转盘(转盘被分成相等的三个扇形).
游戏规则是:
如果所摸球上的数字与转盘转出的数字之和为2,那么游戏者获胜.求游戏者获胜的概率.
驶向胜利的彼岸
用心领“悟”
1
2
3
做一做
是“玩家”就玩出水平
驶向胜利的彼岸
做一做
准备两组相同的牌,每组两张,两张牌面的数字分别是1和2。从两组牌中各摸出一张,则两张牌面数字之和可能有哪些值?
想一想,摸到两张牌的牌面数字之和为2的概率是几?为3、为4呢?
用实际行动证明我能行
知识的升华
拓 展
《史记》中有这样一个故事:有一天,喜欢赛马的齐王要田忌和他赛马,规定每个人从自己的上、中、下三等马中各选一匹来赛。当时,齐王的每一等次的马比田忌同样等次的马都要强。而双方的上等马比中等马强,中等马比下等马强。齐王的马出场是固定的,先后分别为上等马、中等马、下等马,经过孙膑的出谋划策,最终田忌神奇式的赢了,问田忌的出马顺序如何?用你所学的知识加以说明田忌战略的优越性。
大家听过田忌赛马的故事吗?
回味无穷
某一事件发生的可能性大小的这个数,可表示为概率。
利用树状图或表格可以清晰地表示出某个事件发生的所有可能出现的结果;
从而较方便地求出某些事件发生的概率.
小 结
2、本节课你学到了什么?
1、在游戏活动的过程中,你有什么感受?
结束寄语
询问者智之本,思虑者智之道也.
下课了!
