人教版数学七年级下册 7.1.2平面直角坐标系(第一课时) 课件(共24张ppt)
文档属性
| 名称 | 人教版数学七年级下册 7.1.2平面直角坐标系(第一课时) 课件(共24张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-02 20:38:12 | ||
图片预览


文档简介
(共24张PPT)
7.1.2 平面直角坐标系(一)
笛卡尔 ,法国著名哲学家,数学家。1596年出生于法国拉镇,法国巴黎普瓦捷大学毕业,获法律学位。
数学方面的主要成就
哲学专著《方法论》一书中的《几何学》,第一次将x看作点的横坐标,把y看作是点的纵坐标,将平面内的点与一种坐标对应起来。
0
-5
-4
-3
-2
-1
1
2
3
4
5
6
-6
7
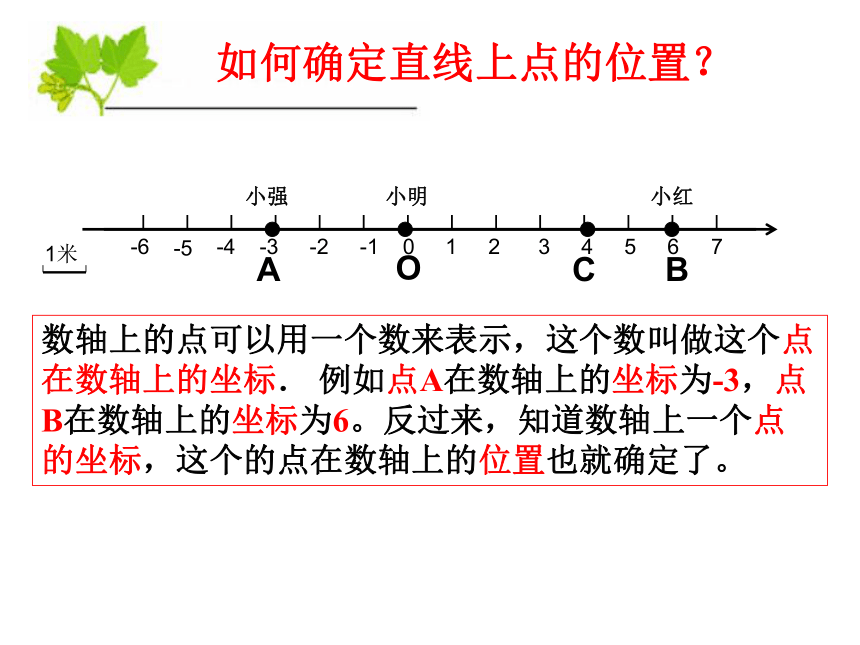
数轴上的点可以用一个数来表示,这个数叫做这个点在数轴上的坐标. 例如点A在数轴上的坐标为-3,点B在数轴上的坐标为6。反过来,知道数轴上一个点的坐标,这个的点在数轴上的位置也就确定了。
A
B
O
C
如何确定直线上点的位置?
小红
小明
小强
1米
小红
小明
小强
如何确定平面上点的位置?
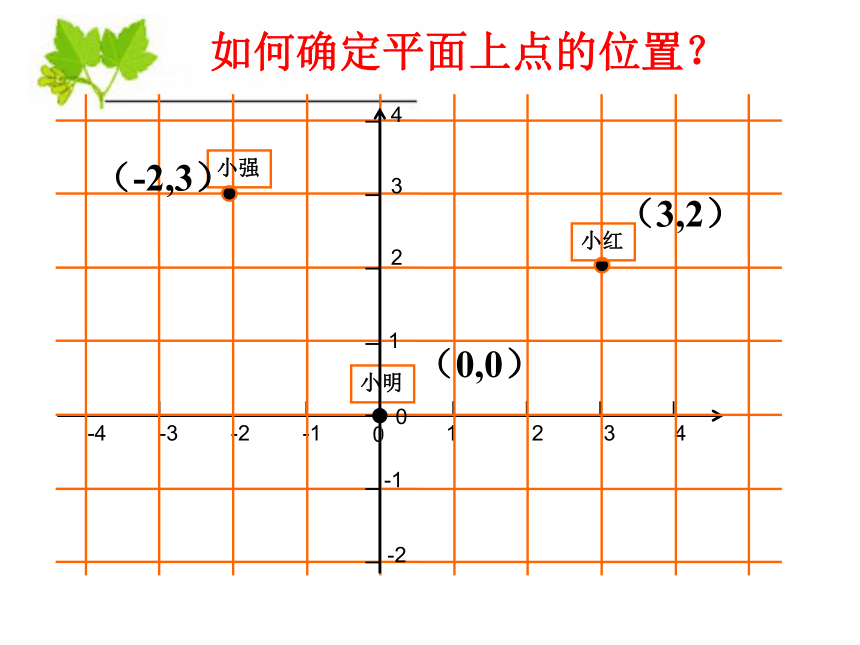
如何确定平面上点的位置?
0
-3
-2
-1
-4
1
2
4
3
小红
小强
小明
0
-2
-1
1
2
4
3
(-2,3)
(0,0)
(3,2)
5
-5
-2
-3
-4
-1
3
2
4
1
-6
6
y
O
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
X
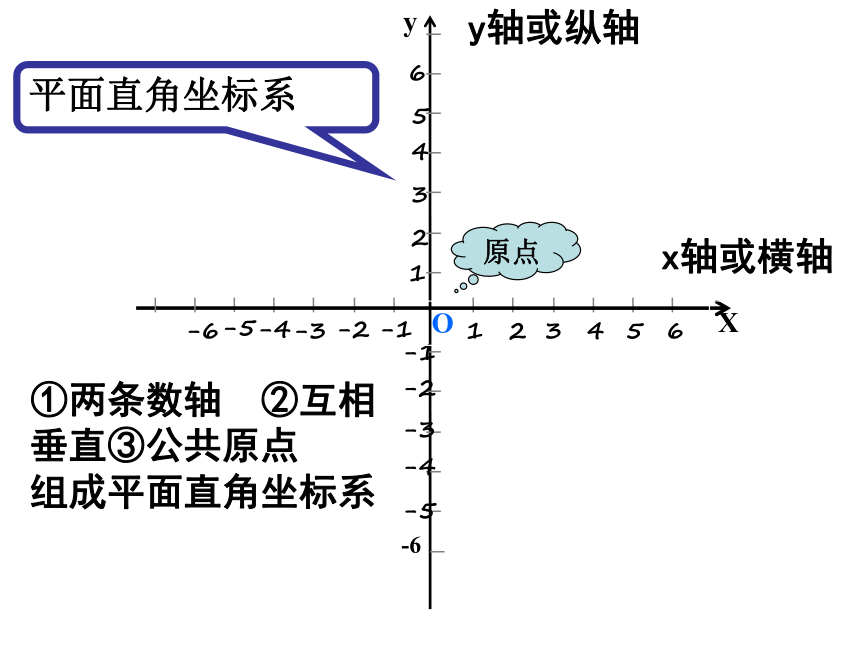
x轴或横轴
y轴或纵轴
原点
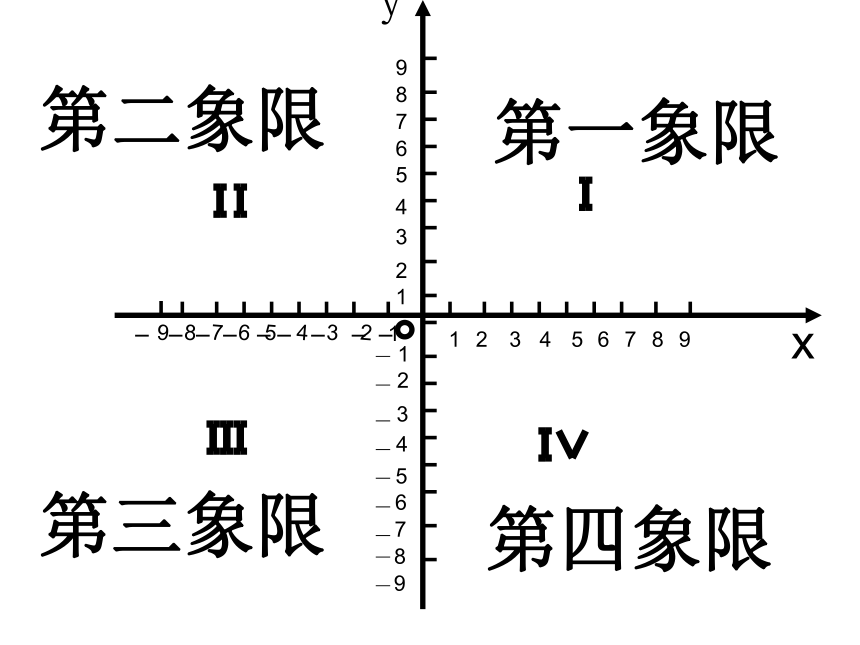
①两条数轴 ②互相垂直③公共原点 组成平面直角坐标系
平面直角坐标系
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
2
3
4
5
6
7
8
9
1
x
y
第一象限
第二象限
第三象限
第四象限
你知道吗?
早在1637年以前,法国数学家、解析几何的创始人笛卡尔受到了经纬度的启发,地理上的经纬度是以赤道和本初子午线为标准的,这两条线从局部上可以看成是平面内互相垂直的两条直线。所以笛卡尔的方法是在平面内画两条互相垂直的数轴,其中水平的数轴叫x轴(或横轴),取向右为正方向,铅直的数轴叫y轴(或纵轴),取向上为正方向,它们的交点是原点,这个平面叫坐标平面。
·
A
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
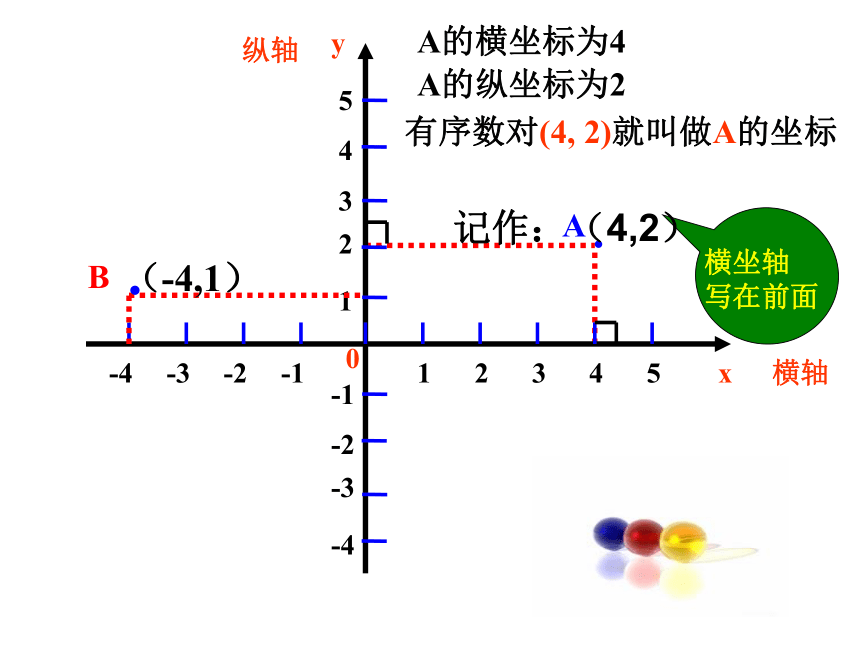
A的横坐标为4
A的纵坐标为2
有序数对(4, 2)就叫做A的坐标
横坐轴
写在前面
·
B
(-4,1)
记作:(4,2)
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
·
B
·
D
·
C
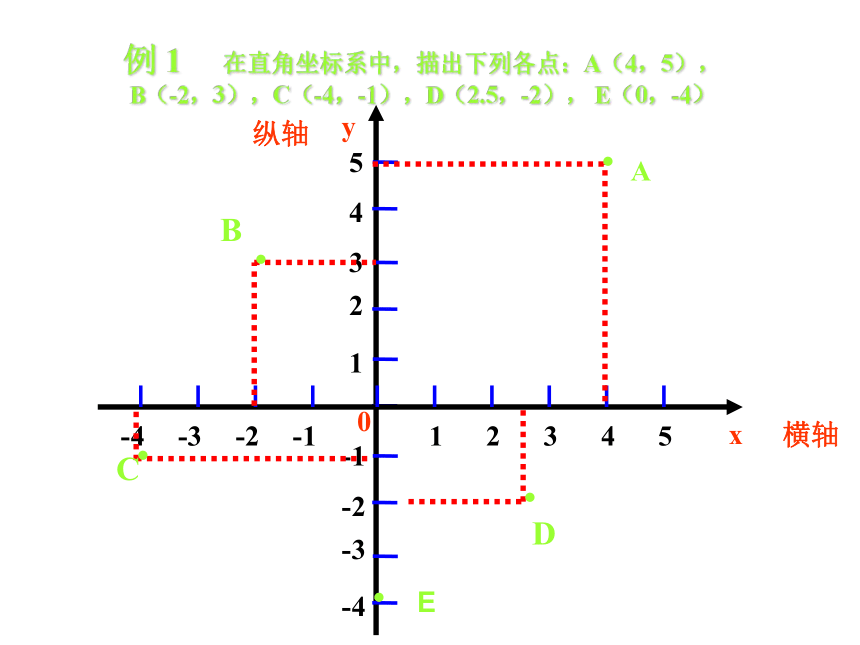
例 1 在直角坐标系中,描出下列各点:A(4,5),
B(-2,3),C(-4,-1),D(2.5,-2), E(0,-4)
·
A
E
·
-1
o
y
x
-2
-6
2
6
2
6
例2 在下图的直角坐标系中描出下列各点,并把各点用线段依次连接起来。观察它是什么形状的图形?
(2,2),(5,6),(-4,6),(-7,2)
平行四边形
x
横轴
坐标是有序
的实数对。
写出图中A、B、C、D、E各点的坐标。
它们分别在哪个象限内
( 3,2 )
( -2,1 )
( -4,- 3 )
( 1,- 2 )
( 2,3 )
0
1
2
3
4
5
-4
-3
-2
-1
·
B
3
1
4
2
5
-2
-4
-1
-3
y
纵轴
·
C
·
A
·
E
·
D
·
-1
o
y
x
-2
-6
2
6
2
练一练 在平面直角坐标系中描出下列各点:
A(-3,-1),B(-3,2),C(0,2),D(3,2),E(3,-1),F(0,-1)
并用线段顺次连接各点,看看你画出的图形是什么形状?
长方形
●
●
●
●
●
●
5
3
4
1
-3
-2
3
1
-5
-3
-4
F
A
B
C
D
E
D
A
B
C
7
y
探究 正方形ABCD中的边长为6 ,如果以点A为坐标原点,AB所在直线为x轴,建立平面直角坐标系,那么Y轴是哪条线?写出正方形的顶点A、B、C、D的坐标.
(O)
(6,0)
(6,6)
(0,6)
(0,0)
想一想
分别写出图中点A、B、C、D的坐标。观察图形,并回答问题
(3,2)
(3,-2)
-2
-1
4
3
2
1
-3
-4
-4
y
1
2
3
-3
-1
-2
(-3,2)
(-3,-2)
0
点A与点B的位置有什么特点
点A与点B的坐标有什么关系
点A与点C的位置有什么特点
点A与点C的坐标有什么关系
点B与点C的位置有什么特点
点B与点C的坐标有什么关系
关于x轴对称的点的横坐标相同,纵坐标互为相反数
关于y轴对称的点的纵坐标相同,横坐标互为相反数
关于原点对称的点的横坐标、纵坐标都互为相反数
A
B
C
D
动一动,方格纸上分别描出下列点的看看这些点在什么位置上,由此你有什么发现?
-4 –3 –2 –1 0
1 2 3 4 5
-1
-2
-3
-4
x
y
A (2,3)
B (2,-1)
C (2,4)
D (2,0)
E (2,-5)
F (2,-4)
A
B
D
E
F
C
●
●
●
●
●
●
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
2
3
4
5
6
7
8
9
1
x
y
说出下列各点的坐标
如何确定平面上点的位置?
0
-3
-2
-1
-4
1
2
4
3
小红
小强
小明
0
-2
-1
1
2
4
3
(-2,3)
(0,0)
(3,2)
小玲
小C
小B
小D
小A
( 2,3 )
( 0,4 )
( -3,-1 )
( -3,-0 )
( 1,-1 )
坐标是有序
数对。
1
2
3
-3
x
-2
·
-2
-3
o
-1
y
4
2
5
3
6
1
在如图建立的直角坐标系中描出下列各组点,并将各组的点用线段依次连接起来.
做
一
做
①(0 , 6), (-4, 3), (4 , 3)
②(-2 , 3), (-2 , -3), (2 , -3), (2 , 3)
·
·
·
·
·
·
观察所得的图形,你觉得它象什么?
-4
-1
4
A(-4,3)
B(4,3)
C(-2,3)
D(2,3)
E(-2,-3)
F(2,-3)
(0 , 6)
·
1
2
3
-3
x
-2
·
-2
-3
o
-1
y
4
2
5
3
6
1
在如图的直角坐标系中读出下列各点.你能发现什么
做
一
做
·
·
·
·
·
·
-4
-1
4
(0 , 6)
·
A
B
C
(0,-3)
(0,3)
D
E
(-2,0)
(2,0)
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
1
2
3
-3
x
-2
·
-2
-3
o
-1
y
4
2
5
3
6
1
做
一
做
·
·
·
·
·
·
-4
-1
4
(-4,3)
(4,3)
(-2,3)
(2,3)
(-2,-3)
(2,-3)
·
在如图建立的直角坐
标系中读出下列各点.你又能发现什么
B
C
D
E
F
G
告诉大家
本节课你的收获!
小结:这节课主要学面直角坐标系的有
关概念和一个最基本的问题,坐标平面内的点
与有序数对是一一对应的,渗透了数形结合
的思想等。
掌握x轴,y轴上点的坐标的特点:
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
纵坐标相同的点的连线平行于x轴
横坐标相同的点的连线平行于y轴
坐标轴的点至少有一个是0
横轴上的点纵坐标为0,
纵坐标上的点横坐标为0.
再 见
7.1.2 平面直角坐标系(一)
笛卡尔 ,法国著名哲学家,数学家。1596年出生于法国拉镇,法国巴黎普瓦捷大学毕业,获法律学位。
数学方面的主要成就
哲学专著《方法论》一书中的《几何学》,第一次将x看作点的横坐标,把y看作是点的纵坐标,将平面内的点与一种坐标对应起来。
0
-5
-4
-3
-2
-1
1
2
3
4
5
6
-6
7
数轴上的点可以用一个数来表示,这个数叫做这个点在数轴上的坐标. 例如点A在数轴上的坐标为-3,点B在数轴上的坐标为6。反过来,知道数轴上一个点的坐标,这个的点在数轴上的位置也就确定了。
A
B
O
C
如何确定直线上点的位置?
小红
小明
小强
1米
小红
小明
小强
如何确定平面上点的位置?
如何确定平面上点的位置?
0
-3
-2
-1
-4
1
2
4
3
小红
小强
小明
0
-2
-1
1
2
4
3
(-2,3)
(0,0)
(3,2)
5
-5
-2
-3
-4
-1
3
2
4
1
-6
6
y
O
-5
5
-3
-4
4
-2
3
-1
2
1
-6
6
X
x轴或横轴
y轴或纵轴
原点
①两条数轴 ②互相垂直③公共原点 组成平面直角坐标系
平面直角坐标系
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
2
3
4
5
6
7
8
9
1
x
y
第一象限
第二象限
第三象限
第四象限
你知道吗?
早在1637年以前,法国数学家、解析几何的创始人笛卡尔受到了经纬度的启发,地理上的经纬度是以赤道和本初子午线为标准的,这两条线从局部上可以看成是平面内互相垂直的两条直线。所以笛卡尔的方法是在平面内画两条互相垂直的数轴,其中水平的数轴叫x轴(或横轴),取向右为正方向,铅直的数轴叫y轴(或纵轴),取向上为正方向,它们的交点是原点,这个平面叫坐标平面。
·
A
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
A的横坐标为4
A的纵坐标为2
有序数对(4, 2)就叫做A的坐标
横坐轴
写在前面
·
B
(-4,1)
记作:(4,2)
3
1
4
2
5
-2
-4
-1
-3
0
1
2
3
4
5
-4
-3
-2
-1
x
横轴
y
纵轴
·
B
·
D
·
C
例 1 在直角坐标系中,描出下列各点:A(4,5),
B(-2,3),C(-4,-1),D(2.5,-2), E(0,-4)
·
A
E
·
-1
o
y
x
-2
-6
2
6
2
6
例2 在下图的直角坐标系中描出下列各点,并把各点用线段依次连接起来。观察它是什么形状的图形?
(2,2),(5,6),(-4,6),(-7,2)
平行四边形
x
横轴
坐标是有序
的实数对。
写出图中A、B、C、D、E各点的坐标。
它们分别在哪个象限内
( 3,2 )
( -2,1 )
( -4,- 3 )
( 1,- 2 )
( 2,3 )
0
1
2
3
4
5
-4
-3
-2
-1
·
B
3
1
4
2
5
-2
-4
-1
-3
y
纵轴
·
C
·
A
·
E
·
D
·
-1
o
y
x
-2
-6
2
6
2
练一练 在平面直角坐标系中描出下列各点:
A(-3,-1),B(-3,2),C(0,2),D(3,2),E(3,-1),F(0,-1)
并用线段顺次连接各点,看看你画出的图形是什么形状?
长方形
●
●
●
●
●
●
5
3
4
1
-3
-2
3
1
-5
-3
-4
F
A
B
C
D
E
D
A
B
C
7
y
探究 正方形ABCD中的边长为6 ,如果以点A为坐标原点,AB所在直线为x轴,建立平面直角坐标系,那么Y轴是哪条线?写出正方形的顶点A、B、C、D的坐标.
(O)
(6,0)
(6,6)
(0,6)
(0,0)
想一想
分别写出图中点A、B、C、D的坐标。观察图形,并回答问题
(3,2)
(3,-2)
-2
-1
4
3
2
1
-3
-4
-4
y
1
2
3
-3
-1
-2
(-3,2)
(-3,-2)
0
点A与点B的位置有什么特点
点A与点B的坐标有什么关系
点A与点C的位置有什么特点
点A与点C的坐标有什么关系
点B与点C的位置有什么特点
点B与点C的坐标有什么关系
关于x轴对称的点的横坐标相同,纵坐标互为相反数
关于y轴对称的点的纵坐标相同,横坐标互为相反数
关于原点对称的点的横坐标、纵坐标都互为相反数
A
B
C
D
动一动,方格纸上分别描出下列点的看看这些点在什么位置上,由此你有什么发现?
-4 –3 –2 –1 0
1 2 3 4 5
-1
-2
-3
-4
x
y
A (2,3)
B (2,-1)
C (2,4)
D (2,0)
E (2,-5)
F (2,-4)
A
B
D
E
F
C
●
●
●
●
●
●
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
1
2
3
4
5
6
7
8
9
2
3
4
5
6
7
8
9
1
x
y
说出下列各点的坐标
如何确定平面上点的位置?
0
-3
-2
-1
-4
1
2
4
3
小红
小强
小明
0
-2
-1
1
2
4
3
(-2,3)
(0,0)
(3,2)
小玲
小C
小B
小D
小A
( 2,3 )
( 0,4 )
( -3,-1 )
( -3,-0 )
( 1,-1 )
坐标是有序
数对。
1
2
3
-3
x
-2
·
-2
-3
o
-1
y
4
2
5
3
6
1
在如图建立的直角坐标系中描出下列各组点,并将各组的点用线段依次连接起来.
做
一
做
①(0 , 6), (-4, 3), (4 , 3)
②(-2 , 3), (-2 , -3), (2 , -3), (2 , 3)
·
·
·
·
·
·
观察所得的图形,你觉得它象什么?
-4
-1
4
A(-4,3)
B(4,3)
C(-2,3)
D(2,3)
E(-2,-3)
F(2,-3)
(0 , 6)
·
1
2
3
-3
x
-2
·
-2
-3
o
-1
y
4
2
5
3
6
1
在如图的直角坐标系中读出下列各点.你能发现什么
做
一
做
·
·
·
·
·
·
-4
-1
4
(0 , 6)
·
A
B
C
(0,-3)
(0,3)
D
E
(-2,0)
(2,0)
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
1
2
3
-3
x
-2
·
-2
-3
o
-1
y
4
2
5
3
6
1
做
一
做
·
·
·
·
·
·
-4
-1
4
(-4,3)
(4,3)
(-2,3)
(2,3)
(-2,-3)
(2,-3)
·
在如图建立的直角坐
标系中读出下列各点.你又能发现什么
B
C
D
E
F
G
告诉大家
本节课你的收获!
小结:这节课主要学面直角坐标系的有
关概念和一个最基本的问题,坐标平面内的点
与有序数对是一一对应的,渗透了数形结合
的思想等。
掌握x轴,y轴上点的坐标的特点:
x轴上的点的纵坐标为0,表示为(x,0)
y轴上的点的横坐标为0,表示为(0,y)
纵坐标相同的点的连线平行于x轴
横坐标相同的点的连线平行于y轴
坐标轴的点至少有一个是0
横轴上的点纵坐标为0,
纵坐标上的点横坐标为0.
再 见
