人教版数学七年级下册 5.2.1平行线 (1) 课件(共30张ppt)
文档属性
| 名称 | 人教版数学七年级下册 5.2.1平行线 (1) 课件(共30张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-02 00:00:00 | ||
图片预览









文档简介
(共32张PPT)
同位角、内错角、同旁内角的特点:
与被截直线的关系 与截线的关系
同位角
内错角
同旁内角
被截直线的同一方向
被截直线的内部
被截直线的内部
截线的同侧
截线的两侧
截线的同侧
“三线八角”回顾
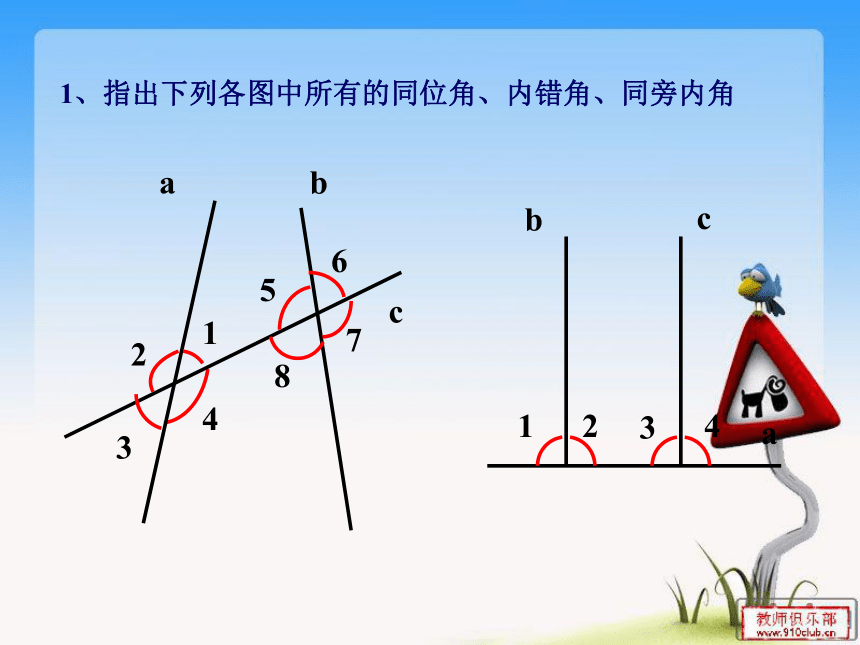
1、指出下列各图中所有的同位角、内错角、同旁内角
a
b
c
8
4
3
2
1
7
6
5
b
c
a
1
4
3
2
在同一水平面上,不相交的两条直线呢?
两条直线相交有几个交点?相交的两条直线有什么特殊的位置关系?
看一看,它们有什么共同之处?
扶手
双杠
铁轨
1、平行线的定义
在同一平面内,不相交的两条直线叫做平行线。
(1)如果没有“同一平面内”,不相交的两条直线平行吗?
(2)定义中的“直线”能改成“线段或射线”吗?
想一想
线段或射线的平行,是指它们所在的直线的平行。
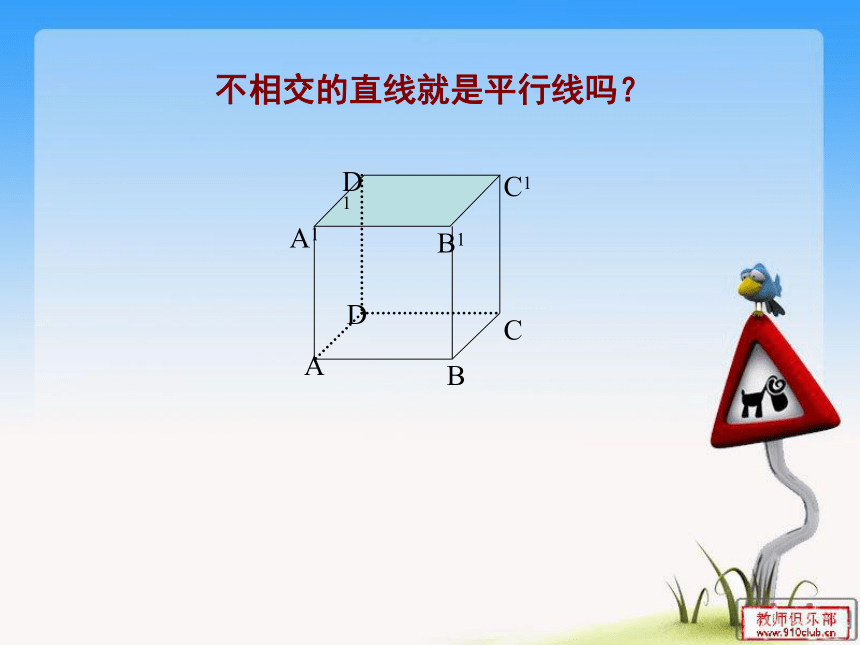
不相交的直线就是平行线吗?
A
B
C
D
A1
B1
C1
D1
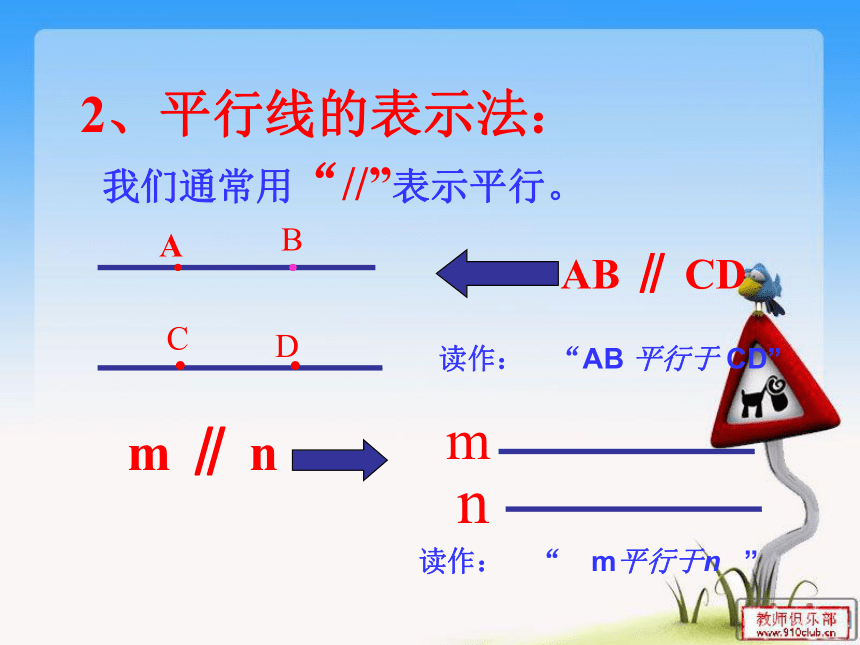
我们通常用“//”表示平行。
2、平行线的表示法:
C
D
B
A
·
·
·
·
m ∥ n
AB ∥ CD
m
n
读作: “AB 平行于 CD”
读作: “ m平行于n ”
在同一平面内,两条不重合 的直线的位置关系只有两种:
相交或平行
在同一平面内,两条直线有几
种位置关系呢?
观察如图所示的长方体后填空:
(1)用符号表示下列两棱的位置关系:
A1B1 AB, AA1 AB,
A1D1 C1D1, AD BC。
(2) A1B1与BC所在的直线是两条不
相交的直线,他们 平行。
(填“是”或“不是”),
由此可知,在 内,两条
不相交的直线才能叫做平行线。
∥
∥
⊥
⊥
同一平面
C
B
D
B1
A1
A
C1
D1
不是
想一想:日常生活中有
哪些例子给你不相交的
形象?
很多国家的国旗上都有平行线
古巴国旗
俄罗斯国旗
比利时国旗
荷兰国旗
阿根廷国旗
你喜欢滑雪吗?早在5000年前,人们就把滑雪作为雪上旅行的一种方式。
滑雪运动最关键的是要保持
两只雪橇板的平行!
短池游泳
双杠
火车轨道
平行线的画法:
一落
二靠
三推
四画
·
把三角尺的一边落在直线上
紧靠三角尺的另一边放一直尺
把三角尺沿直尺的边推到三角尺
的第一边恰好经过点P的位置
沿三角尺的这一边画直线
过直线AB外一点P作直线AB的平行线,看看你能作出吗?能作出几条?
·
A
B
P
动手实践
经过直线外一点,有且只有一条直线与这条直线平行.(平行公理)
说明:人们在长期实践中总结出来的结论叫基本事实,也称为公理,它可以作为以后推理的依据.
由以上的实践你发现了什么?
说说看
如图:三条直线a、b、c。如果a//c,b//c,
那么直线a与b有什么关系?
F
E
b
a
假设a与b相交,
设a与b相交于O
因为a//c,b//c
于是过点O就有两条直线a
b都与c平行。
根据平行公理,这是不可能的
也就是说,a与b不能相交,
只能平行。
O
c
平行公理的推论:
如果两条直线都和第三条直线平行,
那么这两条直线也互相平行
几何语言表达:
a//c , c//b(已知)
a//b(如果两条直线都和第三条直线平行,
那么这两条直线也互相平行)
c
b
a
1、下列说法正确的个数是( )
(1)两条直线不相交就平行。
(2)在同一平面内,两条平行的直线有且只有一个交点
(3)过一点有且只有一条直线与已知直线平行
(4)平行于同一直线的两条直线互相平行
(5)两直线的位置关系只有相交与平行
A、0 B、1 C、2 D、4
B
2、下列推理正确的是( )
A、因为a // d,b // c,所以c // d;
B、因为a // c,b // d,所以c // d;
C、因为a // b,a // c,所以b // c;
D、因为a // b,c // d,所以a // c。
C
3、已知直线L1与L2都经过点P,并且L1//L3,L2//L3,那么L1与L2必须重合,这是因为
经过直线外一点,有且只有一条直线与已知直线平行。
4、下列说法正确的是( )
A、一条直线的平行线有且只有一条
B、经过一点有且只有一条直线与已知直线平行
C、经过一点有两条直线与某一直线平行
D、过直线外一点有且只有一条直线与已知直线平行
D
5、完成下列推理,并在括号内注明理由。
(1)如图1所示,因为AB // DE,BC // DE(已知)。所以
A,B,C三点___________( )
(2)如图2所示,因为AB // CD,CD // EF(已知),所以
________ // _________( )
·
·
·
A
D
E
B
C
图 1
A
B
C
D
E
F
图 2
在同一直线上
经过直线外一点,有且只有一条直线与这条直线平行
AB
EF
如果两条直线都和第三条直线平行,
那么这两条直线也互相平行
6、如图所示,
(1)过BC上任意一点P画AB的平行线交AC于T;
(2)过C画MN//AB;
(3)直线PT,MN是何种位置关系?试说明理由。
A
B
C
P
如图,直线a ∥b,b∥c,c∥d,那么a ∥d吗?为什么?
a
b
c
d
解: 因为 a ∥b,b∥c,
所以 a ∥c ( )
如果两条直线都与第三条直线平行,那么这两条直线互相平行
如果两条直线都与第三条直线平行,那么这两条直线互相平行
因为 c∥d,
所以 a ∥d
( )
四、回顾小结,
突出重点
1、什么是平行线?
2、平行线的表示方法
3、平行线的画法
4、平行线的公理及推论
5、在同一平面内两条直线的位置关系
本节课里我的收获是……
P179 习题5.2第1、2题
同位角、内错角、同旁内角的特点:
与被截直线的关系 与截线的关系
同位角
内错角
同旁内角
被截直线的同一方向
被截直线的内部
被截直线的内部
截线的同侧
截线的两侧
截线的同侧
“三线八角”回顾
1、指出下列各图中所有的同位角、内错角、同旁内角
a
b
c
8
4
3
2
1
7
6
5
b
c
a
1
4
3
2
在同一水平面上,不相交的两条直线呢?
两条直线相交有几个交点?相交的两条直线有什么特殊的位置关系?
看一看,它们有什么共同之处?
扶手
双杠
铁轨
1、平行线的定义
在同一平面内,不相交的两条直线叫做平行线。
(1)如果没有“同一平面内”,不相交的两条直线平行吗?
(2)定义中的“直线”能改成“线段或射线”吗?
想一想
线段或射线的平行,是指它们所在的直线的平行。
不相交的直线就是平行线吗?
A
B
C
D
A1
B1
C1
D1
我们通常用“//”表示平行。
2、平行线的表示法:
C
D
B
A
·
·
·
·
m ∥ n
AB ∥ CD
m
n
读作: “AB 平行于 CD”
读作: “ m平行于n ”
在同一平面内,两条不重合 的直线的位置关系只有两种:
相交或平行
在同一平面内,两条直线有几
种位置关系呢?
观察如图所示的长方体后填空:
(1)用符号表示下列两棱的位置关系:
A1B1 AB, AA1 AB,
A1D1 C1D1, AD BC。
(2) A1B1与BC所在的直线是两条不
相交的直线,他们 平行。
(填“是”或“不是”),
由此可知,在 内,两条
不相交的直线才能叫做平行线。
∥
∥
⊥
⊥
同一平面
C
B
D
B1
A1
A
C1
D1
不是
想一想:日常生活中有
哪些例子给你不相交的
形象?
很多国家的国旗上都有平行线
古巴国旗
俄罗斯国旗
比利时国旗
荷兰国旗
阿根廷国旗
你喜欢滑雪吗?早在5000年前,人们就把滑雪作为雪上旅行的一种方式。
滑雪运动最关键的是要保持
两只雪橇板的平行!
短池游泳
双杠
火车轨道
平行线的画法:
一落
二靠
三推
四画
·
把三角尺的一边落在直线上
紧靠三角尺的另一边放一直尺
把三角尺沿直尺的边推到三角尺
的第一边恰好经过点P的位置
沿三角尺的这一边画直线
过直线AB外一点P作直线AB的平行线,看看你能作出吗?能作出几条?
·
A
B
P
动手实践
经过直线外一点,有且只有一条直线与这条直线平行.(平行公理)
说明:人们在长期实践中总结出来的结论叫基本事实,也称为公理,它可以作为以后推理的依据.
由以上的实践你发现了什么?
说说看
如图:三条直线a、b、c。如果a//c,b//c,
那么直线a与b有什么关系?
F
E
b
a
假设a与b相交,
设a与b相交于O
因为a//c,b//c
于是过点O就有两条直线a
b都与c平行。
根据平行公理,这是不可能的
也就是说,a与b不能相交,
只能平行。
O
c
平行公理的推论:
如果两条直线都和第三条直线平行,
那么这两条直线也互相平行
几何语言表达:
a//c , c//b(已知)
a//b(如果两条直线都和第三条直线平行,
那么这两条直线也互相平行)
c
b
a
1、下列说法正确的个数是( )
(1)两条直线不相交就平行。
(2)在同一平面内,两条平行的直线有且只有一个交点
(3)过一点有且只有一条直线与已知直线平行
(4)平行于同一直线的两条直线互相平行
(5)两直线的位置关系只有相交与平行
A、0 B、1 C、2 D、4
B
2、下列推理正确的是( )
A、因为a // d,b // c,所以c // d;
B、因为a // c,b // d,所以c // d;
C、因为a // b,a // c,所以b // c;
D、因为a // b,c // d,所以a // c。
C
3、已知直线L1与L2都经过点P,并且L1//L3,L2//L3,那么L1与L2必须重合,这是因为
经过直线外一点,有且只有一条直线与已知直线平行。
4、下列说法正确的是( )
A、一条直线的平行线有且只有一条
B、经过一点有且只有一条直线与已知直线平行
C、经过一点有两条直线与某一直线平行
D、过直线外一点有且只有一条直线与已知直线平行
D
5、完成下列推理,并在括号内注明理由。
(1)如图1所示,因为AB // DE,BC // DE(已知)。所以
A,B,C三点___________( )
(2)如图2所示,因为AB // CD,CD // EF(已知),所以
________ // _________( )
·
·
·
A
D
E
B
C
图 1
A
B
C
D
E
F
图 2
在同一直线上
经过直线外一点,有且只有一条直线与这条直线平行
AB
EF
如果两条直线都和第三条直线平行,
那么这两条直线也互相平行
6、如图所示,
(1)过BC上任意一点P画AB的平行线交AC于T;
(2)过C画MN//AB;
(3)直线PT,MN是何种位置关系?试说明理由。
A
B
C
P
如图,直线a ∥b,b∥c,c∥d,那么a ∥d吗?为什么?
a
b
c
d
解: 因为 a ∥b,b∥c,
所以 a ∥c ( )
如果两条直线都与第三条直线平行,那么这两条直线互相平行
如果两条直线都与第三条直线平行,那么这两条直线互相平行
因为 c∥d,
所以 a ∥d
( )
四、回顾小结,
突出重点
1、什么是平行线?
2、平行线的表示方法
3、平行线的画法
4、平行线的公理及推论
5、在同一平面内两条直线的位置关系
本节课里我的收获是……
P179 习题5.2第1、2题
