14.1 三角形中的边角关系(1)
图片预览






文档简介
课件25张PPT。14.1 三角形中的边角关系(1)
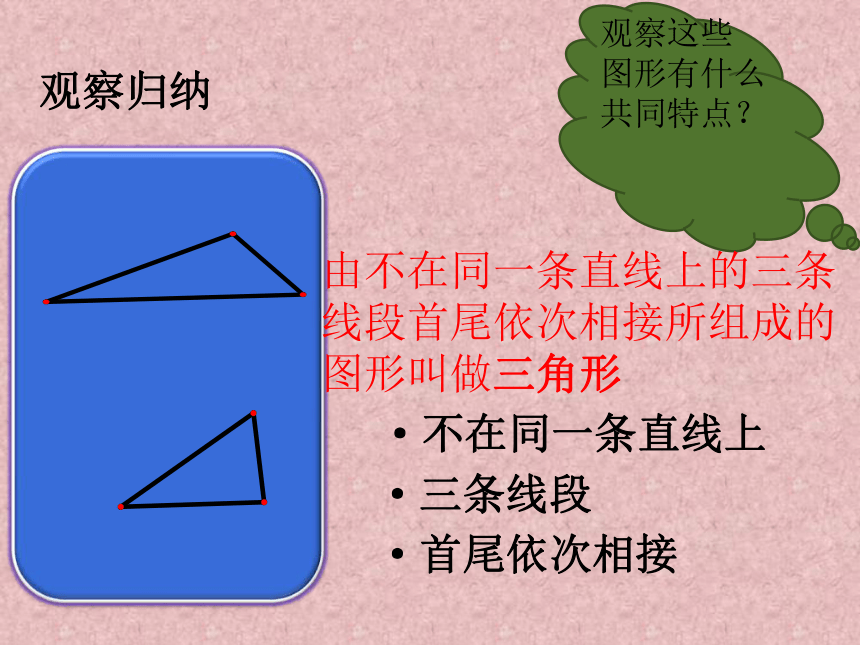
马鞍山市新博初中:夏明荣观察归纳由不在同一条直线上的三条
线段首尾依次相接所组成的
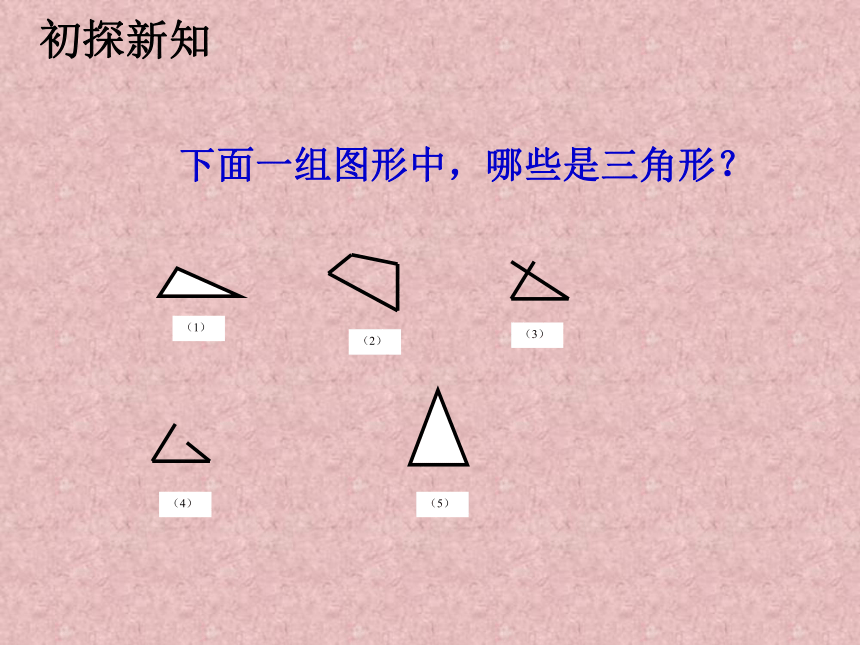
图形叫做三角形·不在同一条直线上·三条线段·首尾依次相接 下面一组图形中,哪些是三角形? (1)(2)(3)(5)(4)初探新知自学课本68页,思考:1234不等边三角形等腰三角形腰腰底边三角形按边分分 注意按边分是两类不是三类,等边三角形是特殊的等腰三角形。
等边三角形两类不是三类如图所示,你能找到几个三角形? 请分别表示出来。 EF国庆节晚上,小明从A地到B地后再往C地走,并到达C地 ,小红直接从 A地到C地。如图所示,小明和小红谁走的路程长?依据是什么?AC任意画一个三角形,测量三边的长度,比较其中任意
两边的长度和与第三边长度的大小关系,你可以得出什
么结论? 动手实践三角形中任何两边的和大于第三边?思考:是否任意三条线段都能构成三角形?并非任意长度的三条线段都能构一个三角形。讨论:在一个三角形中,它的三边具有怎么样的大小关系呢?交流探究 AB+AC>BC;AC+BC>AB; AB+BC>AC.三角形中任何两边的和大于第三边。根据不等式的性质,我们不难得到:|AB-AC|为什么?
⑴2cm、7cm、3cm
⑵1cm、4cm、5cm
⑶5cm、0.6dm、10cm 例题解析,再探新知注意单位要一致小结:判断三条线段是否可以组成三角形,只需说明两条较短线段之和大于第三条线段即可。例题解析,再探新知例2 :一线段长为7,另一线段长为2,那么
用长度为4的线段能和它们拼成三角形吗?
长度为11的线段呢?若能拼成,则第三条
边应在什么范围呢?
变式:三角形的三边分别为4cm、6cm、a
⑴第三边a 的取值范围为_______;
⑵a为偶数时,则a的取值为_________.例:等腰三角形中周长为18cm
1、如果腰长是底边长的2倍,求各边的长;
2、如果一边长为4cm,求另两边的长。例题解析,再探新知解决此类问题时,注意方程思想和分类讨论思想,我们以后会经常用到这些数学思想哦!
巩固练习,强化新知 用下列长度的三条线段能否组成一个三角形?
(1)1cm、2cm、3cm; (2)2cm、3cm、4cm;
(3)4cm、5cm、6cm; (4)5cm、6cm、10cm.
以长4 cm 的线段为底构造一个等腰三角形,
这个三角形的腰长有什么限制?若以整数a、b、c为三边长的三角形,满足
等式(2a-b)2+|7-b| = 0,则这样的三角形的
周长最小值是 ,最大值是 。巩固练习,强化新知已知a、b、c是三角形的三条边,化简|a+b-c|+|c-b-a|.三边都是整数且其最大的边长为4,
那么满足条件的三角形有几种情形?备用师生互动,总结新知:这节课你学习了哪些知识?你收获了哪些数
学思想方法?你还体验到了什么?三角形任何两边的和大于第三边.注意“任何”两宇,如三角形的三边分别为a、b、c,则a+b>c,a+c>b,b+c>a都成立才可以,但如果确定了最长的一条线段,只要其余两条线段之和大于最长的一条,它们必定可以构成三角角形.如果已有两条线段,要确定第三条应该是什么样的长度才能使它们构成三角形?第三边的取值范围是大于这两边的差而小于这两边的和.作业设计,深化新知:习题14.1 第1题,第7题; 若一等腰三角形两边长分别是2和5,求这个等腰三角形的周长。再见
马鞍山市新博初中:夏明荣观察归纳由不在同一条直线上的三条
线段首尾依次相接所组成的
图形叫做三角形·不在同一条直线上·三条线段·首尾依次相接 下面一组图形中,哪些是三角形? (1)(2)(3)(5)(4)初探新知自学课本68页,思考:1234不等边三角形等腰三角形腰腰底边三角形按边分分 注意按边分是两类不是三类,等边三角形是特殊的等腰三角形。
等边三角形两类不是三类如图所示,你能找到几个三角形? 请分别表示出来。 EF国庆节晚上,小明从A地到B地后再往C地走,并到达C地 ,小红直接从 A地到C地。如图所示,小明和小红谁走的路程长?依据是什么?AC任意画一个三角形,测量三边的长度,比较其中任意
两边的长度和与第三边长度的大小关系,你可以得出什
么结论? 动手实践三角形中任何两边的和大于第三边?思考:是否任意三条线段都能构成三角形?并非任意长度的三条线段都能构一个三角形。讨论:在一个三角形中,它的三边具有怎么样的大小关系呢?交流探究 AB+AC>BC;AC+BC>AB; AB+BC>AC.三角形中任何两边的和大于第三边。根据不等式的性质,我们不难得到:|AB-AC|
⑴2cm、7cm、3cm
⑵1cm、4cm、5cm
⑶5cm、0.6dm、10cm 例题解析,再探新知注意单位要一致小结:判断三条线段是否可以组成三角形,只需说明两条较短线段之和大于第三条线段即可。例题解析,再探新知例2 :一线段长为7,另一线段长为2,那么
用长度为4的线段能和它们拼成三角形吗?
长度为11的线段呢?若能拼成,则第三条
边应在什么范围呢?
变式:三角形的三边分别为4cm、6cm、a
⑴第三边a 的取值范围为_______;
⑵a为偶数时,则a的取值为_________.例:等腰三角形中周长为18cm
1、如果腰长是底边长的2倍,求各边的长;
2、如果一边长为4cm,求另两边的长。例题解析,再探新知解决此类问题时,注意方程思想和分类讨论思想,我们以后会经常用到这些数学思想哦!
巩固练习,强化新知 用下列长度的三条线段能否组成一个三角形?
(1)1cm、2cm、3cm; (2)2cm、3cm、4cm;
(3)4cm、5cm、6cm; (4)5cm、6cm、10cm.
以长4 cm 的线段为底构造一个等腰三角形,
这个三角形的腰长有什么限制?若以整数a、b、c为三边长的三角形,满足
等式(2a-b)2+|7-b| = 0,则这样的三角形的
周长最小值是 ,最大值是 。巩固练习,强化新知已知a、b、c是三角形的三条边,化简|a+b-c|+|c-b-a|.三边都是整数且其最大的边长为4,
那么满足条件的三角形有几种情形?备用师生互动,总结新知:这节课你学习了哪些知识?你收获了哪些数
学思想方法?你还体验到了什么?三角形任何两边的和大于第三边.注意“任何”两宇,如三角形的三边分别为a、b、c,则a+b>c,a+c>b,b+c>a都成立才可以,但如果确定了最长的一条线段,只要其余两条线段之和大于最长的一条,它们必定可以构成三角角形.如果已有两条线段,要确定第三条应该是什么样的长度才能使它们构成三角形?第三边的取值范围是大于这两边的差而小于这两边的和.作业设计,深化新知:习题14.1 第1题,第7题; 若一等腰三角形两边长分别是2和5,求这个等腰三角形的周长。再见
