华东师大版数学九年级上册第23章 图形的相似 23.4 中位线(教案)
文档属性
| 名称 | 华东师大版数学九年级上册第23章 图形的相似 23.4 中位线(教案) |

|
|
| 格式 | docx | ||
| 文件大小 | 51.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-03 08:32:16 | ||
图片预览

文档简介
23.4 中位线
教学目标
1、知识与技能目标
(1)掌握三角形的中位线的概念和定理。
(2)了解三角形重心及其性质。
2、过程与方法目标
灵活运用三角形中位线解决有关问题。
3、情感态度价值观目标
结合实际问题,进一步理解三角形中位线的概念及性质,培养创造性思维。
重点难点
重点:理解并应用三角形中位线定理。
难点:三角形中位线定理的证明与应用。
教学过程
一、旧知回顾
1、相似三角形有哪些性质?
2、相似三角形有哪些判定方法?
二、问题探究
活动一:
1、画出三角形,找出三边的中点
2、连接6点中的任意两点(如图1)
3、找找哪些线是你已经学过的,哪些是未曾学过的
(
A
) (
A
) (
C
B
F
E
D
)
(
D
) (
E
) (
D
) (
E
)
(
C
)
(
C
) (
B
) (
F
) (
B
)
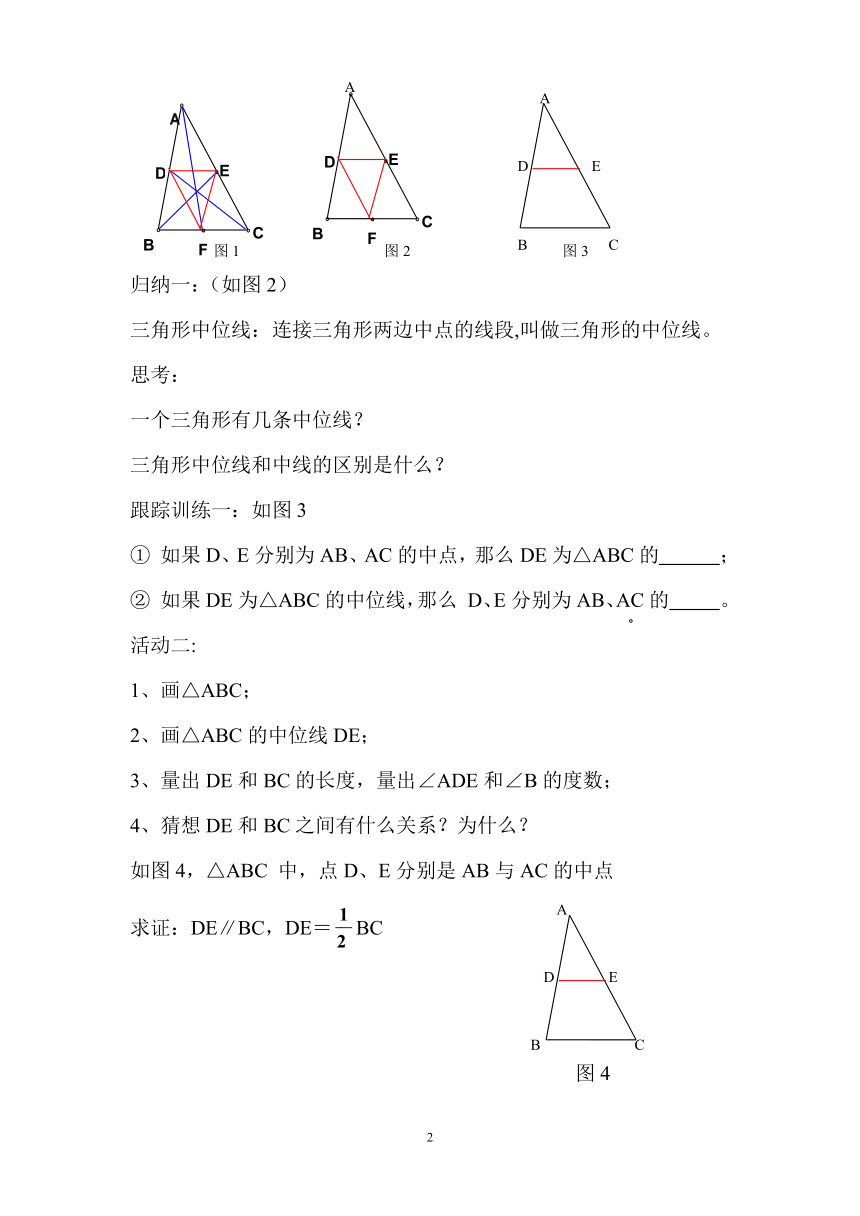
图1 图2 图3
归纳一:(如图2)
三角形中位线:连接三角形两边中点的线段,叫做三角形的中位线。
思考:
一个三角形有几条中位线?
三角形中位线和中线的区别是什么?
跟踪训练一:如图3
① 如果D、E分别为AB、AC的中点,那么DE为△ABC的 ;
② 如果DE为△ABC的中位线,那么 D、E分别为AB、AC的 。
活动二:
1、画△ABC;
2、画△ABC的中位线DE;
3、量出DE和BC的长度,量出∠ADE和∠B的度数;
4、猜想DE和BC之间有什么关系?为什么?
如图4,△ABC 中,点D、E分别是AB与AC的中点
(
A
)求证:DE∥BC,DE=BC
(
D
) (
E
)
(
C
) (
B
)
图4
证明:∵点D、E分别是AB与AC的中点
∴
∵∠A=∠A
∴△ADE∽△ABC
∴∠ADE=∠ABC,
∴DE∥BC,且DE=BC
归纳二:三角形的中位线平行于第三边且等于第三边的一半。
(
A
)符号语言:
(
E
) (
D
)如图5,∵ DE是△ABC的中位线
(
B
) (
C
) ∴ DE∥BC,DE=BC
说一说 图5
A、B两点被池塘隔开,如何才能知道它们之间的距离呢?
(
A
) (
B
)在AB外选一点C,连结AC和BC,并分别找出AC和BC的中点M、N,连接MN,如果测得MN = 20m,那么A、B两点的距离是多少?为什么?
(
F
)
(
E
) (
D
) (
D
)跟踪练习二:
(
C
) (
B
) (
A
) (
C
) (
E
)
图6 图7
1、如图6:在△ABC中,DE是中位线
(1)若∠ADE=60°,则∠B= 度
(2)若BC=8cm,则DE= cm
(3)若DE=5cm,则BC= cm
2.如图7:在△ABC中,D、E、F分别是各边中点,
AB=6cm,AC=8cm,BC=10cm, 则△DEF
的周长= cm
三、知识应用与拓展
例1 求证三角形的一条中位线与第三边上的中线互相平分.
已知:如图8所示,在△ABC中,
AD=DB,BE=EC,AF=FC.
求证:AE、DF互相平分 图8
【分析】要证AE、DF互相平分,即要证四边形ADEF为平行四边形.证明:连结DE、EF,
∵AD=DB,BE=EC,
∴DE∥AC,同理可得EF∥BA.
∴四边形ADEF是平行四边形.
∴AE、DF互相平分.
例2 如图9,△ABC中,D、E分别是边BC、AB的中点,AD、CE相交于G.
求证:
图9
【分析】有两边中点易想到连接两边中点构造三角形的中位线.
证明:连接ED,
∵ D、E分别是边BC、AB的中点,
∴ DE∥AC, ,
∴△ACG∽△DEG ,
∴ ,
∴ 图10
思考:在例2的图中取AC的中点F,假设BF与AD相交于点G′,如图10,那么我们同理可得,即两图中的G与G′是重合的,由此我们可以得出什么结论
归纳三:三角形三条边上的中线交于一点,这个点就是三角形的重心, 重心与一边中点的连线的长是对应中线长的.
四、师生互动,课堂小结
1、三角形中位线的概念
2、三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.
3、三角形中位线定理的应用.
4、三角形重心的性质.
五、课后作业
1、练习第1题
2、习题23.4第1题
(
5
)
教学目标
1、知识与技能目标
(1)掌握三角形的中位线的概念和定理。
(2)了解三角形重心及其性质。
2、过程与方法目标
灵活运用三角形中位线解决有关问题。
3、情感态度价值观目标
结合实际问题,进一步理解三角形中位线的概念及性质,培养创造性思维。
重点难点
重点:理解并应用三角形中位线定理。
难点:三角形中位线定理的证明与应用。
教学过程
一、旧知回顾
1、相似三角形有哪些性质?
2、相似三角形有哪些判定方法?
二、问题探究
活动一:
1、画出三角形,找出三边的中点
2、连接6点中的任意两点(如图1)
3、找找哪些线是你已经学过的,哪些是未曾学过的
(
A
) (
A
) (
C
B
F
E
D
)
(
D
) (
E
) (
D
) (
E
)
(
C
)
(
C
) (
B
) (
F
) (
B
)
图1 图2 图3
归纳一:(如图2)
三角形中位线:连接三角形两边中点的线段,叫做三角形的中位线。
思考:
一个三角形有几条中位线?
三角形中位线和中线的区别是什么?
跟踪训练一:如图3
① 如果D、E分别为AB、AC的中点,那么DE为△ABC的 ;
② 如果DE为△ABC的中位线,那么 D、E分别为AB、AC的 。
活动二:
1、画△ABC;
2、画△ABC的中位线DE;
3、量出DE和BC的长度,量出∠ADE和∠B的度数;
4、猜想DE和BC之间有什么关系?为什么?
如图4,△ABC 中,点D、E分别是AB与AC的中点
(
A
)求证:DE∥BC,DE=BC
(
D
) (
E
)
(
C
) (
B
)
图4
证明:∵点D、E分别是AB与AC的中点
∴
∵∠A=∠A
∴△ADE∽△ABC
∴∠ADE=∠ABC,
∴DE∥BC,且DE=BC
归纳二:三角形的中位线平行于第三边且等于第三边的一半。
(
A
)符号语言:
(
E
) (
D
)如图5,∵ DE是△ABC的中位线
(
B
) (
C
) ∴ DE∥BC,DE=BC
说一说 图5
A、B两点被池塘隔开,如何才能知道它们之间的距离呢?
(
A
) (
B
)在AB外选一点C,连结AC和BC,并分别找出AC和BC的中点M、N,连接MN,如果测得MN = 20m,那么A、B两点的距离是多少?为什么?
(
F
)
(
E
) (
D
) (
D
)跟踪练习二:
(
C
) (
B
) (
A
) (
C
) (
E
)
图6 图7
1、如图6:在△ABC中,DE是中位线
(1)若∠ADE=60°,则∠B= 度
(2)若BC=8cm,则DE= cm
(3)若DE=5cm,则BC= cm
2.如图7:在△ABC中,D、E、F分别是各边中点,
AB=6cm,AC=8cm,BC=10cm, 则△DEF
的周长= cm
三、知识应用与拓展
例1 求证三角形的一条中位线与第三边上的中线互相平分.
已知:如图8所示,在△ABC中,
AD=DB,BE=EC,AF=FC.
求证:AE、DF互相平分 图8
【分析】要证AE、DF互相平分,即要证四边形ADEF为平行四边形.证明:连结DE、EF,
∵AD=DB,BE=EC,
∴DE∥AC,同理可得EF∥BA.
∴四边形ADEF是平行四边形.
∴AE、DF互相平分.
例2 如图9,△ABC中,D、E分别是边BC、AB的中点,AD、CE相交于G.
求证:
图9
【分析】有两边中点易想到连接两边中点构造三角形的中位线.
证明:连接ED,
∵ D、E分别是边BC、AB的中点,
∴ DE∥AC, ,
∴△ACG∽△DEG ,
∴ ,
∴ 图10
思考:在例2的图中取AC的中点F,假设BF与AD相交于点G′,如图10,那么我们同理可得,即两图中的G与G′是重合的,由此我们可以得出什么结论
归纳三:三角形三条边上的中线交于一点,这个点就是三角形的重心, 重心与一边中点的连线的长是对应中线长的.
四、师生互动,课堂小结
1、三角形中位线的概念
2、三角形中位线定理:三角形的中位线平行于第三边,并且等于第三边的一半.
3、三角形中位线定理的应用.
4、三角形重心的性质.
五、课后作业
1、练习第1题
2、习题23.4第1题
(
5
)
