必修一模块备考试题

必修一模块备考试题
一、选择题
1.已知,，则等于( )
A.{x|x∈R} B.　{y|y≥0}
C.{(0,0)，(1,1)} D.　
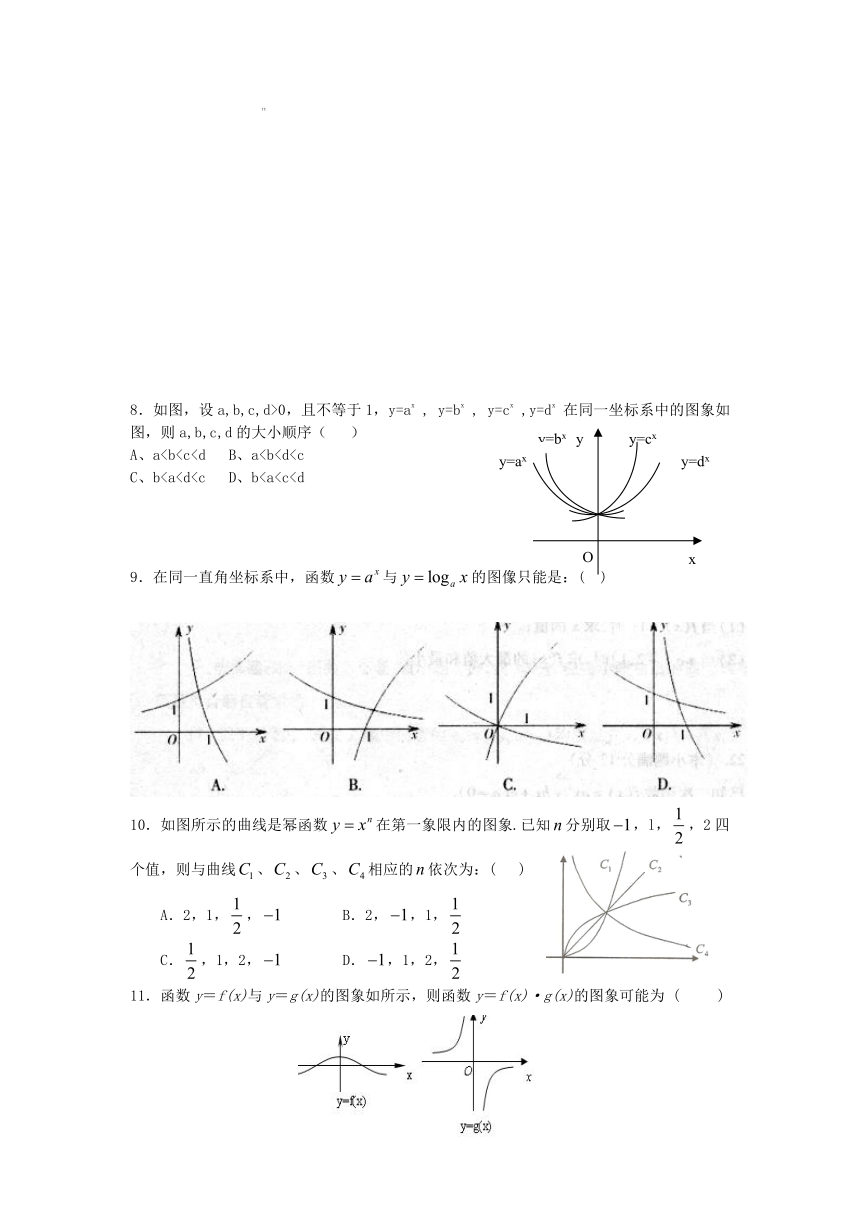
2. 下列四个函数中，在(0，+∞)上为增函数的是( )
A.f(x)=3-x B.f(x)=x2-3x
C.f(x)=- D.f(x)=－|x|
1．若偶函数在上是增函数，则下列关系式中成立的是（ ）
A． B．
C． D．
3.函数f(x)=x2+2(a－1)x+2在区间　(-∞，4］上递减，则a的取值范围是( )
A.［-3,+∞) B.(-∞,-3］
C.(-∞,5］ D.［3,+∞)
4. 已知函数f(x)=的定义域是一切实数，则m的取值范围是( )
A.05．下列函数是偶函数的是：( )
A． B． C． D．
7．设是奇函数，且在内是增函数，又，则的解集是（ ）
A． B．
C． D．
6．已知0A.第一象限; B.第二象限; C.第三象限; D.第四象限
7. 二次函数y=ax2+bx与指数函数y=()x的图象只可能是( )
8．如图，设a,b,c,d>0，且不等于1，y=ax , y=bx , y=cx ,y=dx 在同一坐标系中的图象如图，则a,b,c,d的大小顺序（ ）
A、aC、b9．在同一直角坐标系中，函数与的图像只能是：( )
10．如图所示的曲线是幂函数在第一象限内的图象.已知分别取，l，，2四个值，则与曲线、、、相应的依次为：( )
A．2，1，， B．2，，1，
C．，1，2， D．，1，2，
11．函数y＝f(x)与y＝g(x)的图象如所示，则函数y＝f(x)·g(x)的图象可能为 ( )
12．下列说法正确的是：( )
A．对于任何实数，都成立
B．对于任何实数，都成立
C．对于任何实数，总有
D．对于任何正数，总有
13.若指数函数在[-1，1]上的最大值与最小值的差是1，则底数为：( )
A. B. C. D.
14、若a=0.32，b=log20.3，c=20.3，则a、b、c的大小关系是 （ ）
A、a15． （ ）
A 有最大值，但无最小值 B 有最小值，有最大值1
C 有最小值1，有最大值 D 无最大值，也无最小值
6．若是偶函数，其定义域为，且在上是减函数，则的大小关系是（ ）
A．> B．<
C． D．
16. 函数设，则使函数的定义域为R且为奇函数的所有值为( )
A　1，3 　　 B　，1 　　 C　，3 　　 D　，1，3
17.已知偶函数f(x)在(－∞,0)上单调递增，对于任意x1<0,x2>0,若∣x1∣<∣x2∣,则有( )
A.f(－x1)> f(－x2) B.f(－x1)﹤ f(－x2)
C.－f(－x1)> f(－x2) D.－f(－x1)﹤ f(－x2)
18．，则的取值范围是 （ ）
A． B． C． D．
19．对任意实数,规定取三个值中的最小值，则函数 （ ）
A、有最大值2，最小值1 B、有最大值2，无最小值
C、有最大值1，无最小值 D、无最大值，无最小值
20．下列说法正确的是 （ ）
A．函数的图象与直线可能有两个交点；
B．函数与函数是同一函数；
C．对于上的函数，若有，那么函数在内有零点；
D．对于指数函数()与幂函数(),总存在一个,当 时,就会有。
21． 方程根的情况是 （ ）
A.有两个正根 B.一个正根一个负根 C.有两个负根 D.仅有一个实数根
22．函数的零点所在区间为：( )
A． B． C． D．
二、填空题
23．定义集合运算A*B={m| m=xy(x-y) ,}.设集合A={1，2}，B={3, 4},则A*B中所有元素之和为
24．已知幂函数y=f(x)的图象过点(2,)，则f(9)= 。
25.已知，则 .26. 方程 的解是 ．27．已知函数，则的值是
28．已知函数,则其值域为___________
29. 函数y=的最大值是_______.
30. 关于下列命题：
①若函数的定义域是｛，则它的值域是；
② 若函数的定义域是，则它的值域是；
③若函数的值域是，则它的定义域一定是；
④若函数的值域是，则它的定义域是.
其中不正确的命题的序号是_____________( 注：把你认为不正确的命题的序号都填上).
31. 已知函数满足：
(1) 对于任意的,有；
(2)对于任意的，当时有，
请写出一个满足这些条件的函数 。（写出一个即可）
32．已知方程的一个根大于0，另一个根小于-2，则实数a的取值范围是 。
33．已知函数为偶函数,其定义域为,则a的值为
34．已知为奇函数，当时,，则当时,
10．设是上的奇函数，且当时，，则当时_____________________。
35. 求值：
（1）；
.
（1） ．
36．已知集合，
（1）求； （2）若，求的取值范围。
37．已知函数是定义在R上的偶函数，且当≤0时，．
(1)现已画出函数在y轴左侧的图像，如图所示，请补出完整函数的图像，并根据图像写出函数的增区间；
(2)写出函数的解析式和值域.
38．已知，求函数的最大值和最小值.
39. 设a>0, 是R上的偶函数。
（1）求a的值。
（2）解方程 。
(3)探究该函数的单调性。
40．设函数,
确定的值,使为奇函数并求此时的值域.
41．已知甲、乙两个工厂在今年的1月份的利润都是6万元，且甲厂在2月份的利润是14万元，乙厂在2月份的利润是8万元.若甲、乙两个工厂的利润（万元）与月份之间的函数关系式分别符合下列函数模型：，，
．
（1）求甲、乙两个工厂今年5月份的利润；
（2）在同一直角坐标系下画出函数与的草图，
并根据草图比较今年甲、乙两个工厂的利润的大小情况．
42.某租赁公司拥有汽车100辆，当每辆车的月租金为3000元时，可全部租出。当每辆车的月租金每增加50元时，未租出的车将会增加一辆。租出的车每辆每月需要维护费150元，未租出的车每辆每月需要维护费50元。
（1）当每辆车的月租金定为3600元时，能租出多少辆车？
（2）当每辆车的月租金定为多少元时，租赁公司的月收益最大？最大月收益是多少？
44. 已知函数,当时,恒有.
(1). 求证: (2). 若试用表示
(3). 如果x＞0时,且,试求在区间上的最大值和最小值.
45．已知函数.
（1）求函数的定义域；
（2）判断的奇偶性；
（3）方程是否有根？如果有根，请求出一个长度为的区间，使；如果没有，请说明理由？（注：区间的长度）．
46．探究函数,x∈(0,+∞)的最小值，并确定相应的x的值，列表如下：
x
…
0.5
1
1.5
1.7
1.9
2
2.1
2.2
2.3
3
4
5
7
…
y
…
8.5
5
4.17
4.05
4.005
4
4.005
4.102
4.24
4.3
5
5.8
7.57
…
请观察表中y值随x值变化的特点，完成下列问题：
(1)若函数,(x>0)在区间(0,2)上递减，则在 上递增；
(2)当x= 时，,(x>0)的最小值为 ；
(3)试用定义证明,(x>0)在区间(0,2)上递减；
(4)函数,(x<0)有最值吗？是最大值还是最小值？此时x为何值？（直接回答，不需证明）
47.已知函数
（1）若且函数的值域为,求的表达式;
（2）在（1）的条件下, 当时, 是单调函数, 求实数k的取值范围;
（3）设, 且为偶函数, 判断＋能否大于零?请说明理由。
48.已知函数是定义在上的函数,若对于任意,都有，且＞0时,有＞0
⑴ 判断函数的奇偶性；
⑵ 判断函数在上是增函数，还是减函数，并用单调性定义证明你的结论；
⑶ 设,若＜ ,对所有,恒成立,求实数的取值范围.
必修一模块备考试题参考答案
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
C
B
D
B
A
A
C
D
A
A
A
13
14
15
16
17
18
19
20
21
22
B
C
C
A
A
A
B
D
A
B
二、填空题
23.-34 24.3 25. f (x)=(x－1) 26. 27 1/9 28. 29.4,
30. ①②③ 31. 32. (-∞,-1) 33.1 34.

三、解答题
35．解：（1）原式=
==108+2-7-3=100
36．解：（1）
（2）
37．(1)补出完整函数图像得3分.
的递增区间是，.
（2）解析式为
值域为
（注意：将两个区间“并”起来，扣2分；）
38．解：令
令
，
又∵对称轴，
∴当，即
当即x=0时，
39.解：（1）a=1 （2）x=0
40. 为奇函数, ,即,
解得:
, ,,

所以的值域为
41．解：（1）依题意：由，有，解得：
∴；
由，有，解得：
∴．
所以甲在今年5月份的利润为万元，乙在今年5月份的利润为万元，故有，即甲、乙两个工厂今年5月份的利润相等.
（2）作函数图象如右：
从图中，可以看出今年甲、乙两个工厂的利润：
当或时，有；
当时，有；
当时，有
42.解：（1）当每辆车的月租金定为3600元时，设未租出辆车
则 （辆）
故 能租出88辆车
（2）设未租出辆车有辆，则已租出车辆有辆，租赁公司的月收益为
则 （）
（）
（）
当时 取最大值为307050 （元）
月租金为（元）
答：当每辆车的月租金定为4050元时，租赁公司的月收益最大.最大月收益是307050元.
解法2（2）设每辆本的月租金定为元，
则租赁公司的月收益为：，
整理得：。
所以，当时，最大，其最大值为。
即当每辆车的月租金定为4050元时，租赁公司的月收益最大，最大收益为307050元。
43．解：
（2）
又， 且在为单调递减函数，
∴在为单调递增函数。
，或，
或，或
解得，或不存在，或，或不存在，
综上的取值范围为
另解：要

。
44: (1)令得,再令得
(2)由.
(3)设,则=
,,
在R上是减函
数,,
45．解：（1）要使函数有意义，则，∴，故函数的定义域为
（2）∵，∴为奇函数．
（3）由题意知方程等价于，
可化为
设，
则，，
所以，故方程在上必有根；
又因为，
所以，故方程在上必有一根．
所以满足题意的一个区间为．
46．解：(1) (2,+∞) (左端点可以闭) (2)x=2时，ymin=4
(3) 设0f(x1)- f(x2)=
=
∵0∴f(x1)- f(x2)>0 ∴f(x1)> f(x2)
∴f(x)在区间(0,2)上递减。
(4) 有最大值-4，此时x= -2。
47 ∵,
∴ ①
又函数的值域为, 所以
且由知即 ②
由①②得

∴.
∴
（2） 由（1）有
,
当或时,
即或时, 是具有单调性.
（3） ∵是偶函数
∴ ∴,
∵设则.又
∴
∴＋,
∴＋能大于零.
48.解：（1）令，则
令 ，则，
是奇函数.
(2) 函数在上是增函数.
设 且 则
又
即
故 由函数单调性定义可知，函数在上是增函数.
（3）设，若＜，对所有,恒成立.
则必须 恒成立；
即 恒成立
令 必须 即
解得
故 实数的取值范围为 .