1.3 带电粒子在组合场中的运动 课件(48张PPT)
文档属性
| 名称 | 1.3 带电粒子在组合场中的运动 课件(48张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-01-01 16:39:32 | ||
图片预览









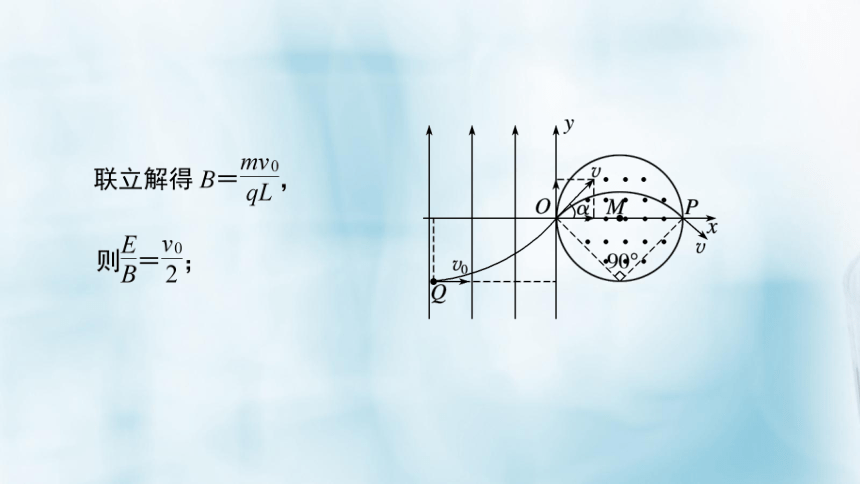
文档简介
(共48张PPT)
带电粒子在电场、磁场组合场中的运动是指粒子从电场到磁场或从磁场到电场的运动。通常按时间的先后顺序分成若干个小过程,在每一运动过程中从粒子的受力性质、受力方向和速度方向的关系入手,分析粒子在电场中做什么运动,在磁场中做什么运动.
1. 解决带电粒子在组合场中的运动所需知识
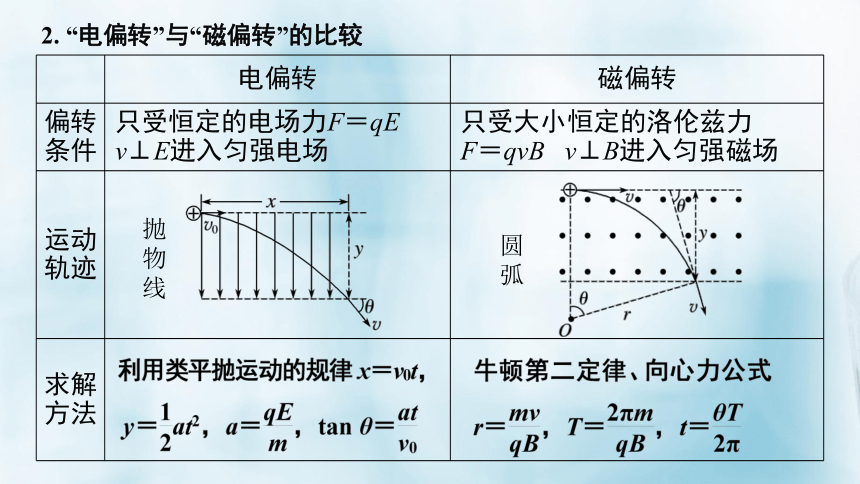
2. “电偏转”与“磁偏转”的比较
电偏转 磁偏转
偏转条件 只受恒定的电场力F=qE
v⊥E进入匀强电场 只受大小恒定的洛伦兹力 F=qvB v⊥B进入匀强磁场
运动轨迹
求解方法
抛
物
线
圆
弧
一、由电场进入磁场
例1 (多选)一带负电粒子的质量为m、电荷量为q,空间中一平行板电容器两极板S1、S2间的电压为U.将此粒子在靠近极板S1的A处无初速度释放,经电场加速后,经O点进入磁感应强度大小为B、方向垂直纸面向里的有
界匀强磁场(右边界平行S2),图中虚线Ox垂直极板S2,当粒子从P点离开磁场时,其速度方向与Ox方向的夹角θ=60°,如图1所示,整个装置处于真空中,不计粒子所受重力,则
图1
√
√
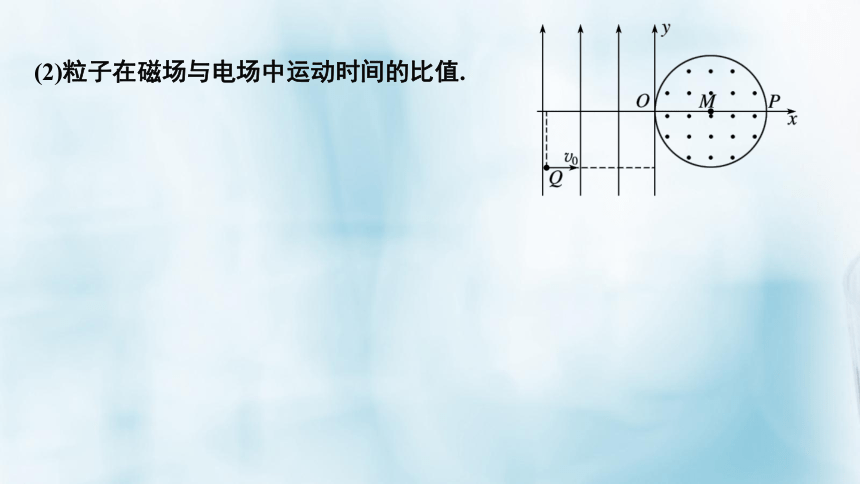
例2 如图2所示,在平面直角坐标系xOy内,第Ⅱ、Ⅲ象限内存在沿y轴正方向的匀强电场,第Ⅰ、Ⅳ象限内存在半径为L的圆形匀强磁场,磁场圆心在M(L,0)点,磁场方向垂直于坐标平面向外.一带正电粒子从第Ⅲ象
图2
限中的Q(-2L,-L)点以速度v0沿x轴正方向射入电场,恰好从坐标原点O进入磁场,从P(2L,0)点射出磁场,不计粒子重力,求:
(1)电场强度与磁感应强度大小的比值;
例2 如图2所示,在平面直角坐标系xOy内,第Ⅱ、Ⅲ象限内存在沿y轴正方向的匀强电场,第Ⅰ、Ⅳ象限内存在半径为L的圆形匀强磁场,磁场圆心在M(L,0)点,磁场方向垂直于坐标平面向外.一带正电粒子从第Ⅲ象
图2
限中的Q(-2L,-L)点以速度v0沿x轴正方向射入电场,恰好从坐标原点O进入磁场,从P(2L,0)点射出磁场,不计粒子重力,求:
(1)电场强度与磁感应强度大小的比值;
(2)粒子在磁场与电场中运动时间的比值.
(2)粒子在磁场与电场中运动时间的比值.
(2)粒子在磁场与电场中运动时间的比值.
总结提升
从电场射出的末速度是进入磁场的初速度,要特别注意求解进入磁场时的速度的大小和方向,这是正确求解的关键.
例3 如图3所示,在平面直角坐标系xOy的第一象限内有竖直向上的匀强电场E,圆心O1在x轴上,半径为R且过坐标原点O,圆内有垂直纸面向外的匀强磁场B(图中未画出).一质量为m,带电荷量为q的正粒子从圆上P
图3
二、由磁场进入电场
点正对圆心O1以速度v0射入磁场,从坐标原点O离开磁场,接着又恰好经过第一象限的Q(a,b)点,已知PO1与x轴负方向成θ角,不计粒子重力,求:
(1)匀强电场E及匀强磁场B的大小;
例3 如图3所示,在平面直角坐标系xOy的第一象限内有竖直向上的匀强电场E,圆心O1在x轴上,半径为R且过坐标原点O,圆内有垂直纸面向外的匀强磁场B(图中未画出).一质量为m,带电荷量为q的正粒子从圆上P
图3
二、由磁场进入电场
点正对圆心O1以速度v0射入磁场,从坐标原点O离开磁场,接着又恰好经过第一象限的Q(a,b)点,已知PO1与x轴负方向成θ角,不计粒子重力,求:
(1)匀强电场E及匀强磁场B的大小;
解析 设粒子在磁场中做圆周运动的半径为r,
粒子从O到Q做类平抛运动,设运动时间为t2,
a=v0t2,
(2)粒子从P运动到Q的时间.
(2)粒子从P运动到Q的时间.
(2)粒子从P运动到Q的时间.
三、多次进出电场和磁场
例4 如图4所示的xOy坐标系,在第二象限内有水平向右的匀强电场,在第一、第四象限内分别存在匀强磁场,磁感应强度大小相等,方向如图所示.现有一个质量为m、电荷量为+q的带电粒子在该平面内从x轴上的P
图4
点,以垂直于x轴的初速度v0进入匀强电场,恰好经过y轴上的Q点且与y轴成45°角射出电场,再经过一段时间又恰好垂直于x轴进入第四象限的磁场.已知O、P之间的距离为d,不计粒子的重力.求:
(1) O点到Q点的距离;
(1) O点到Q点的距离;
答案 2d
解析 设Q点的纵坐标为h,粒子到达Q点的水平分速度为vx,从P到Q受到的恒定的电场力与初速度方向垂直,则粒子在电场中做类平抛运动,则由类平抛运动的规律可知,h=v0t1
解得h=2d.
(2) 磁感应强度B的大小;
(2) 磁感应强度B的大小;
(3)带电粒子自进入电场至在磁场中第二次经过x轴所用的时间.
(3)带电粒子自进入电场至在磁场中第二次经过x轴所用的时间.
1.(粒子由电场进入磁场)(2020·湖南期末)如图5所示,坐标空间中有匀强电场和匀强磁场,电场方向沿y轴负方向,磁场方向垂直于纸面向里,y轴是两种场的分界面,磁场区的宽度为d.现有一质量为m、电荷量为-q
图5
(q>0)的带电粒子从x轴上x=-L的N点处以初速度v0沿x轴正方向开始运动,然后经过y轴上y= 的M点进入磁场,不计带电粒子重力.
(1)求y轴左侧电场的场强大小E;
1.(粒子由电场进入磁场)(2020·湖南期末)如图5所示,坐标空间中有匀强电场和匀强磁场,电场方向沿y轴负方向,磁场方向垂直于纸面向里,y轴是两种场的分界面,磁场区的宽度为d.现有一质量为m、电荷量为-q
图5
(q>0)的带电粒子从x轴上x=-L的N点处以初速度v0沿x轴正方向开始运动,然后经过y轴上y= 的M点进入磁场,不计带电粒子重力.
(1)求y轴左侧电场的场强大小E;
1
2
解析 粒子从N到M做类平抛运动,有L=v0t
(2)若要求粒子能穿越磁场区域而不再返回电场中,求磁感应强度应满足的条件.
(2)若要求粒子能穿越磁场区域而不再返回电场中,求磁感应强度应满足的条件.
解析 粒子进入磁场时的速度大小
如图所示为粒子恰好不穿出磁场时的运动轨迹,粒子在磁场中做匀速圆周运动,
粒子能够穿过磁场,则要求r+rcos 45°>d
2.(粒子多次进、出电场和磁场)(2020·山东高三学业考试)如图6所示,在第一象限内,存在垂直于xOy平面向外的匀强磁场Ⅰ,第二象限内存在水平向右的匀强电场,第三、四象限内存在垂直于xOy平面向外、磁感应强度大小为B0的匀强磁场Ⅱ.一质量为m、电荷量为+q的粒子,从x轴上M点以某一初速度垂直于x轴进入第四象限,在xOy平面内,以原点O为圆心 做半径为R0的
图6
圆周运动;随后进入电场运动至y轴上的N点,沿与y轴正方向成45°角离开电场;在磁场Ⅰ中运动一段时间后,再次垂直于x轴进入第四象限.不计粒子重力.求:
(1)带电粒子从M点进入第四象限时初速度的大小v0;
(1)带电粒子从M点进入第四象限时初速度的大小v0;
(1)带电粒子从M点进入第四象限时初速度的大小v0;
(2)电场强度的大小E;
(2)电场强度的大小E;
(2)电场强度的大小E;
解析 粒子在第二象限内做类平抛运动,沿着平行于x轴方向:qE=ma,
vx2-0=2aR0
沿与y轴正方向成45°角离开电场,所以vx=vy=v0
(3) 磁场Ⅰ中磁感应强度的大小B1.
(3) 磁场Ⅰ中磁感应强度的大小B1.
解析 粒子的轨迹如图所示,
进入第二象限,沿着平行于x轴方向:
沿着平行于y轴方向:
ON=vyt=v0t
所以ON=2R0
带电粒子在电场、磁场组合场中的运动是指粒子从电场到磁场或从磁场到电场的运动。通常按时间的先后顺序分成若干个小过程,在每一运动过程中从粒子的受力性质、受力方向和速度方向的关系入手,分析粒子在电场中做什么运动,在磁场中做什么运动.
1. 解决带电粒子在组合场中的运动所需知识
2. “电偏转”与“磁偏转”的比较
电偏转 磁偏转
偏转条件 只受恒定的电场力F=qE
v⊥E进入匀强电场 只受大小恒定的洛伦兹力 F=qvB v⊥B进入匀强磁场
运动轨迹
求解方法
抛
物
线
圆
弧
一、由电场进入磁场
例1 (多选)一带负电粒子的质量为m、电荷量为q,空间中一平行板电容器两极板S1、S2间的电压为U.将此粒子在靠近极板S1的A处无初速度释放,经电场加速后,经O点进入磁感应强度大小为B、方向垂直纸面向里的有
界匀强磁场(右边界平行S2),图中虚线Ox垂直极板S2,当粒子从P点离开磁场时,其速度方向与Ox方向的夹角θ=60°,如图1所示,整个装置处于真空中,不计粒子所受重力,则
图1
√
√
例2 如图2所示,在平面直角坐标系xOy内,第Ⅱ、Ⅲ象限内存在沿y轴正方向的匀强电场,第Ⅰ、Ⅳ象限内存在半径为L的圆形匀强磁场,磁场圆心在M(L,0)点,磁场方向垂直于坐标平面向外.一带正电粒子从第Ⅲ象
图2
限中的Q(-2L,-L)点以速度v0沿x轴正方向射入电场,恰好从坐标原点O进入磁场,从P(2L,0)点射出磁场,不计粒子重力,求:
(1)电场强度与磁感应强度大小的比值;
例2 如图2所示,在平面直角坐标系xOy内,第Ⅱ、Ⅲ象限内存在沿y轴正方向的匀强电场,第Ⅰ、Ⅳ象限内存在半径为L的圆形匀强磁场,磁场圆心在M(L,0)点,磁场方向垂直于坐标平面向外.一带正电粒子从第Ⅲ象
图2
限中的Q(-2L,-L)点以速度v0沿x轴正方向射入电场,恰好从坐标原点O进入磁场,从P(2L,0)点射出磁场,不计粒子重力,求:
(1)电场强度与磁感应强度大小的比值;
(2)粒子在磁场与电场中运动时间的比值.
(2)粒子在磁场与电场中运动时间的比值.
(2)粒子在磁场与电场中运动时间的比值.
总结提升
从电场射出的末速度是进入磁场的初速度,要特别注意求解进入磁场时的速度的大小和方向,这是正确求解的关键.
例3 如图3所示,在平面直角坐标系xOy的第一象限内有竖直向上的匀强电场E,圆心O1在x轴上,半径为R且过坐标原点O,圆内有垂直纸面向外的匀强磁场B(图中未画出).一质量为m,带电荷量为q的正粒子从圆上P
图3
二、由磁场进入电场
点正对圆心O1以速度v0射入磁场,从坐标原点O离开磁场,接着又恰好经过第一象限的Q(a,b)点,已知PO1与x轴负方向成θ角,不计粒子重力,求:
(1)匀强电场E及匀强磁场B的大小;
例3 如图3所示,在平面直角坐标系xOy的第一象限内有竖直向上的匀强电场E,圆心O1在x轴上,半径为R且过坐标原点O,圆内有垂直纸面向外的匀强磁场B(图中未画出).一质量为m,带电荷量为q的正粒子从圆上P
图3
二、由磁场进入电场
点正对圆心O1以速度v0射入磁场,从坐标原点O离开磁场,接着又恰好经过第一象限的Q(a,b)点,已知PO1与x轴负方向成θ角,不计粒子重力,求:
(1)匀强电场E及匀强磁场B的大小;
解析 设粒子在磁场中做圆周运动的半径为r,
粒子从O到Q做类平抛运动,设运动时间为t2,
a=v0t2,
(2)粒子从P运动到Q的时间.
(2)粒子从P运动到Q的时间.
(2)粒子从P运动到Q的时间.
三、多次进出电场和磁场
例4 如图4所示的xOy坐标系,在第二象限内有水平向右的匀强电场,在第一、第四象限内分别存在匀强磁场,磁感应强度大小相等,方向如图所示.现有一个质量为m、电荷量为+q的带电粒子在该平面内从x轴上的P
图4
点,以垂直于x轴的初速度v0进入匀强电场,恰好经过y轴上的Q点且与y轴成45°角射出电场,再经过一段时间又恰好垂直于x轴进入第四象限的磁场.已知O、P之间的距离为d,不计粒子的重力.求:
(1) O点到Q点的距离;
(1) O点到Q点的距离;
答案 2d
解析 设Q点的纵坐标为h,粒子到达Q点的水平分速度为vx,从P到Q受到的恒定的电场力与初速度方向垂直,则粒子在电场中做类平抛运动,则由类平抛运动的规律可知,h=v0t1
解得h=2d.
(2) 磁感应强度B的大小;
(2) 磁感应强度B的大小;
(3)带电粒子自进入电场至在磁场中第二次经过x轴所用的时间.
(3)带电粒子自进入电场至在磁场中第二次经过x轴所用的时间.
1.(粒子由电场进入磁场)(2020·湖南期末)如图5所示,坐标空间中有匀强电场和匀强磁场,电场方向沿y轴负方向,磁场方向垂直于纸面向里,y轴是两种场的分界面,磁场区的宽度为d.现有一质量为m、电荷量为-q
图5
(q>0)的带电粒子从x轴上x=-L的N点处以初速度v0沿x轴正方向开始运动,然后经过y轴上y= 的M点进入磁场,不计带电粒子重力.
(1)求y轴左侧电场的场强大小E;
1.(粒子由电场进入磁场)(2020·湖南期末)如图5所示,坐标空间中有匀强电场和匀强磁场,电场方向沿y轴负方向,磁场方向垂直于纸面向里,y轴是两种场的分界面,磁场区的宽度为d.现有一质量为m、电荷量为-q
图5
(q>0)的带电粒子从x轴上x=-L的N点处以初速度v0沿x轴正方向开始运动,然后经过y轴上y= 的M点进入磁场,不计带电粒子重力.
(1)求y轴左侧电场的场强大小E;
1
2
解析 粒子从N到M做类平抛运动,有L=v0t
(2)若要求粒子能穿越磁场区域而不再返回电场中,求磁感应强度应满足的条件.
(2)若要求粒子能穿越磁场区域而不再返回电场中,求磁感应强度应满足的条件.
解析 粒子进入磁场时的速度大小
如图所示为粒子恰好不穿出磁场时的运动轨迹,粒子在磁场中做匀速圆周运动,
粒子能够穿过磁场,则要求r+rcos 45°>d
2.(粒子多次进、出电场和磁场)(2020·山东高三学业考试)如图6所示,在第一象限内,存在垂直于xOy平面向外的匀强磁场Ⅰ,第二象限内存在水平向右的匀强电场,第三、四象限内存在垂直于xOy平面向外、磁感应强度大小为B0的匀强磁场Ⅱ.一质量为m、电荷量为+q的粒子,从x轴上M点以某一初速度垂直于x轴进入第四象限,在xOy平面内,以原点O为圆心 做半径为R0的
图6
圆周运动;随后进入电场运动至y轴上的N点,沿与y轴正方向成45°角离开电场;在磁场Ⅰ中运动一段时间后,再次垂直于x轴进入第四象限.不计粒子重力.求:
(1)带电粒子从M点进入第四象限时初速度的大小v0;
(1)带电粒子从M点进入第四象限时初速度的大小v0;
(1)带电粒子从M点进入第四象限时初速度的大小v0;
(2)电场强度的大小E;
(2)电场强度的大小E;
(2)电场强度的大小E;
解析 粒子在第二象限内做类平抛运动,沿着平行于x轴方向:qE=ma,
vx2-0=2aR0
沿与y轴正方向成45°角离开电场,所以vx=vy=v0
(3) 磁场Ⅰ中磁感应强度的大小B1.
(3) 磁场Ⅰ中磁感应强度的大小B1.
解析 粒子的轨迹如图所示,
进入第二象限,沿着平行于x轴方向:
沿着平行于y轴方向:
ON=vyt=v0t
所以ON=2R0
