1.3 带电粒子在磁场中的运动(磁聚焦) 课件(22张PPT)
文档属性
| 名称 | 1.3 带电粒子在磁场中的运动(磁聚焦) 课件(22张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2022-01-01 16:40:44 | ||
图片预览



文档简介
(共22张PPT)
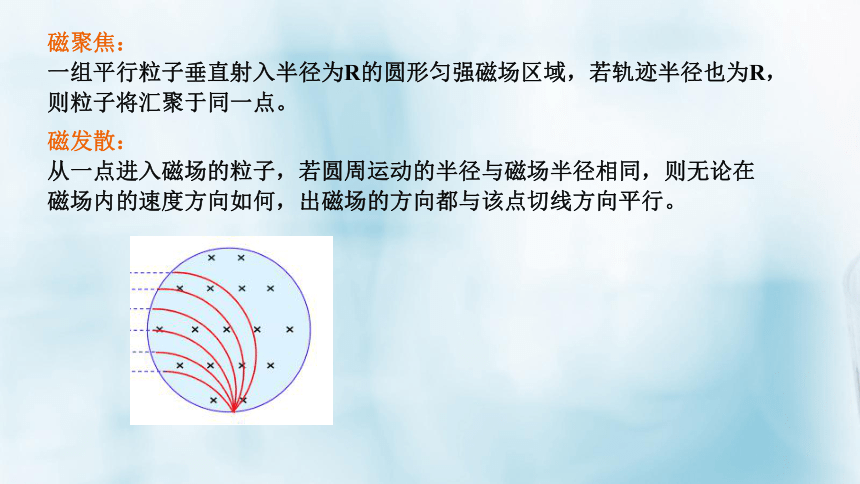
磁聚焦:
一组平行粒子垂直射入半径为R的圆形匀强磁场区域,若轨迹半径也为R,则粒子将汇聚于同一点。
磁聚焦:
一组平行粒子垂直射入半径为R的圆形匀强磁场区域,若轨迹半径也为R,则粒子将汇聚于同一点。
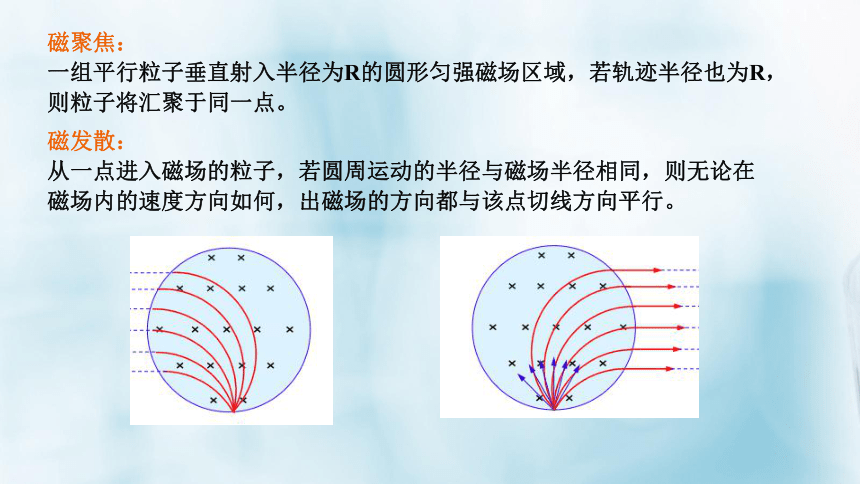
磁发散:
从一点进入磁场的粒子,若圆周运动的半径与磁场半径相同,则无论在磁场内的速度方向如何,出磁场的方向都与该点切线方向平行。
磁聚焦:
一组平行粒子垂直射入半径为R的圆形匀强磁场区域,若轨迹半径也为R,则粒子将汇聚于同一点。
磁发散:
从一点进入磁场的粒子,若圆周运动的半径与磁场半径相同,则无论在磁场内的速度方向如何,出磁场的方向都与该点切线方向平行。
磁聚焦:
一组平行粒子垂直射入半径为R的圆形匀强磁场区域,若轨迹半径也为R,则粒子将汇聚于同一点。
磁发散:
从一点进入磁场的粒子,若圆周运动的半径与磁场半径相同,则无论在磁场内的速度方向如何,出磁场的方向都与该点切线方向平行。
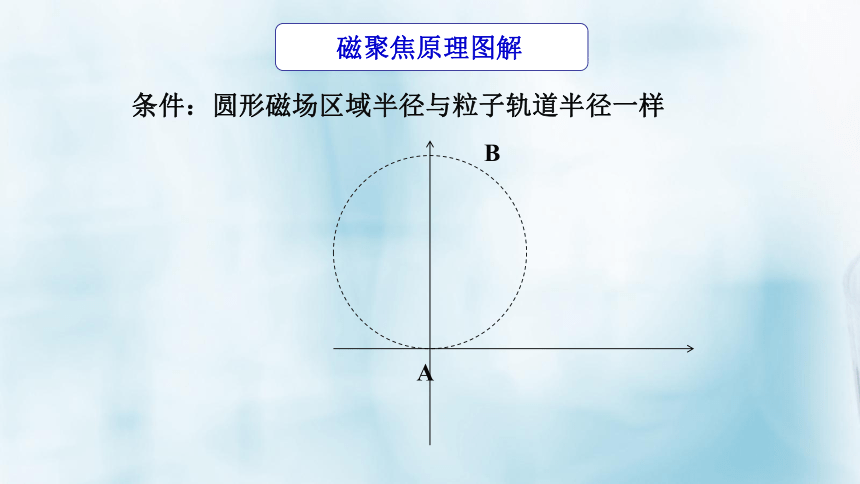
磁聚焦原理图解
条件:圆形磁场区域半径与粒子轨道半径一样
A
B
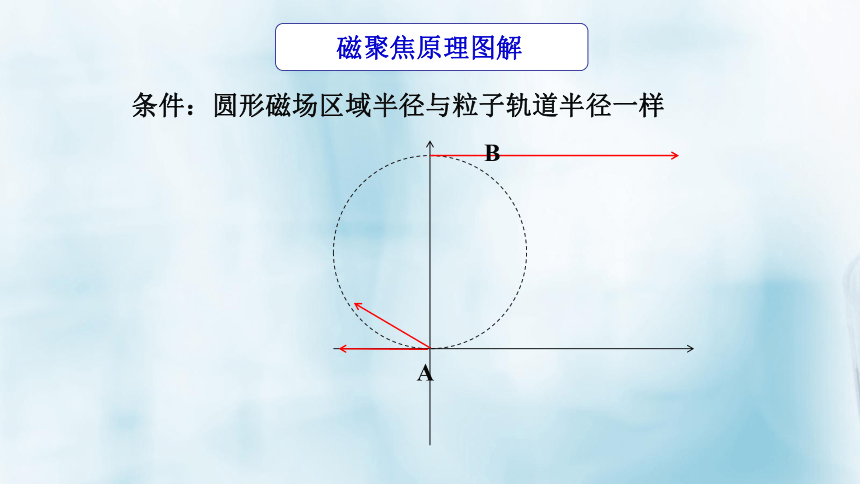
磁聚焦原理图解
条件:圆形磁场区域半径与粒子轨道半径一样
A
B
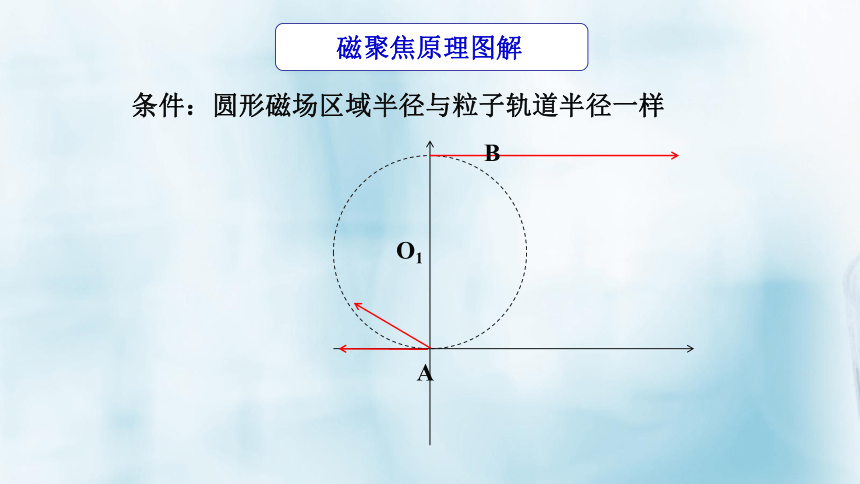
磁聚焦原理图解
条件:圆形磁场区域半径与粒子轨道半径一样
O1
A
B
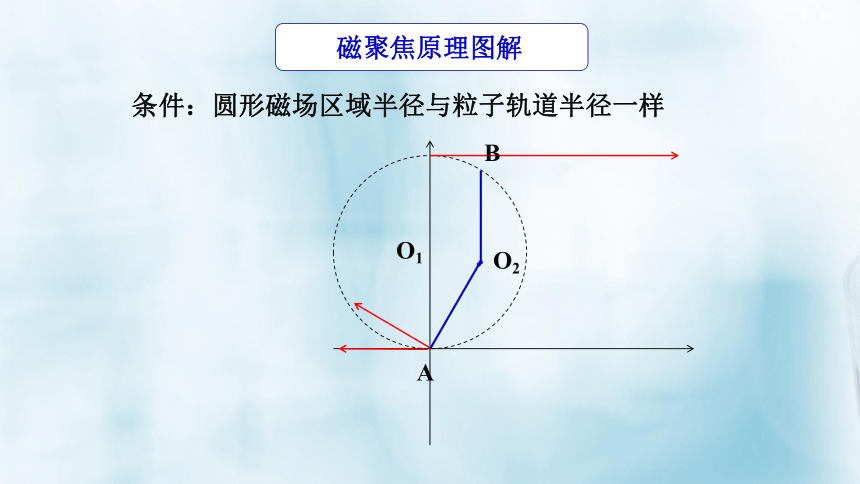
磁聚焦原理图解
条件:圆形磁场区域半径与粒子轨道半径一样
O1
O2
A
B
磁聚焦原理图解
条件:圆形磁场区域半径与粒子轨道半径一样
O1
O2
A
B
例1.(2009年浙江卷)如图,在xOy平面内与y轴平行的匀强电场,在半径为R的圆内还有与xOy平面垂直的匀强磁场。在圆的左边放置一带电微粒发射装置,它沿x轴正方向发射出一束具有相同质量m、电荷量q(q>0)和初速度v的带电微粒。发射时,这束带电微粒分布在0<y<2R的区间内。已知重力加速度大小为g。
(1)从A点射出的带电微粒平行于x轴从C点进入有磁场区域,并从坐标原点O沿y轴负方向离 开,求电场强度和磁感应强度的大 小与方向。
(2)请指出这束带电微粒与x 轴相交的区域,并说明理由。
x
y
R
O/
O
v
带点微粒发射装置
C
P
Q
r
图 (c)
x
y
R
O/
O
v
C
A
x
y
R
O/
v
Q
P
O
R
θ
图(a)
图(b)
【答案】(1) ;方向垂直于纸面向外 (2)见解析 (3) 与x轴相交的区域范围是x>0.
【解析】 略
【关键】 图示
变式:
如图所示,圆心O1的坐标为(0﹑R),半径为R的圆形区域内存在垂直纸面向里的磁感应强度为B的匀强磁场,在坐标原点O处有一粒子源,可向y>0的区域各个方向发射质量为m电量为-q速度为 的粒子,证明:粒子经过该磁场偏转后都能平行于x轴方向运动。
x
y
O
v0
例2:在xoy平面内有很多质量为m,电量为e的电子,从坐标原点O不断以相同速率沿不同方向射入第一象限,如图所示.现加一垂直于xOy平面向里、磁感强度为B的匀强磁场,要求这些入射电子穿过磁场都能平行于x轴且沿x轴正向运动,试问符合该条件的磁场的最小面积为多大?(不考虑电子间的相互作用)
x
y
O
v0
例2:在xoy平面内有很多质量为m,电量为e的电子,从坐标原点O不断以相同速率沿不同方向射入第一象限,如图所示.现加一垂直于xOy平面向里、磁感强度为B的匀强磁场,要求这些入射电子穿过磁场都能平行于x轴且沿x轴正向运动,试问符合该条件的磁场的最小面积为多大?(不考虑电子间的相互作用)
x
y
O
v0
O1
O2
O3
O4
O5
On
x
y
O
v0
例2:在xoy平面内有很多质量为m,电量为e的电子,从坐标原点O不断以相同速率沿不同方向射入第一象限,如图所示.现加一垂直于xOy平面向里、磁感强度为B的匀强磁场,要求这些入射电子穿过磁场都能平行于x轴且沿x轴正向运动,试问符合该条件的磁场的最小面积为多大?(不考虑电子间的相互作用)
x
y
O
v0
O1
O2
O3
O4
O5
On
例2.(2009·海南·T16)如图,ABCD是边长为a的正方形。质量为m电荷量为e的电子以大小为v0的初速度沿纸面垂直于BC边射入正方形区域。在正方形内适当区域中有匀强磁场,电子从BC边上的任意点入射,都只能从A点射出磁场。不计重力。求:
(1)此匀强磁场区域中磁感应强度的大小和方向;
(2)此匀强磁场区域的最小面积。
A
B
C
D
A
B
C
D
x
y
O
v0
A
B
C
D
x
y
O
v0
S=2(πa2/4-a2/2) =(π-2)a2/2
练习1: 如图所示,纸面内有宽为L水平向 右飞行的带电粒子流,粒子质量为m,电 荷量为-q,速率为v0,不考虑粒子的重力 及相互间的作用,要使粒子都汇聚到一点, 可以在粒子流的右侧虚线框内设计一匀强 磁场区域,则磁场区域的形状及对应的磁 感应强度可以是(其中B0=mv0/qL,A、C、 D选项中曲线均为半径是L的圆弧, B选项中曲线为半径是0.5L的圆)( )
练习2:如图所示,在坐标系xOy内有一半径为a的圆形区域,圆心坐标为O1(a,0),圆内分布有垂直纸面向里的匀强磁场。在直线y=a的上方和直线x=2a的左侧区域内,有一沿y轴负方向的匀强电场,场强大小为E。一质量为m、电荷量为+q(q>0)的粒子以速度v从O点垂直于磁场方向射入,当速度方向沿x轴正方向时,粒子恰好从O1点正上方的A点射出磁场,不计粒子重力。
(1) 求磁感应强度B的大小;
(2) 若粒子以速度v从O点垂直于磁场方向 射入第一象限,当速度方向沿x轴正方向的 夹角为30°时,粒子从射入磁场到最终离开 磁场的时间 t。
磁聚焦:
一组平行粒子垂直射入半径为R的圆形匀强磁场区域,若轨迹半径也为R,则粒子将汇聚于同一点。
磁聚焦:
一组平行粒子垂直射入半径为R的圆形匀强磁场区域,若轨迹半径也为R,则粒子将汇聚于同一点。
磁发散:
从一点进入磁场的粒子,若圆周运动的半径与磁场半径相同,则无论在磁场内的速度方向如何,出磁场的方向都与该点切线方向平行。
磁聚焦:
一组平行粒子垂直射入半径为R的圆形匀强磁场区域,若轨迹半径也为R,则粒子将汇聚于同一点。
磁发散:
从一点进入磁场的粒子,若圆周运动的半径与磁场半径相同,则无论在磁场内的速度方向如何,出磁场的方向都与该点切线方向平行。
磁聚焦:
一组平行粒子垂直射入半径为R的圆形匀强磁场区域,若轨迹半径也为R,则粒子将汇聚于同一点。
磁发散:
从一点进入磁场的粒子,若圆周运动的半径与磁场半径相同,则无论在磁场内的速度方向如何,出磁场的方向都与该点切线方向平行。
磁聚焦原理图解
条件:圆形磁场区域半径与粒子轨道半径一样
A
B
磁聚焦原理图解
条件:圆形磁场区域半径与粒子轨道半径一样
A
B
磁聚焦原理图解
条件:圆形磁场区域半径与粒子轨道半径一样
O1
A
B
磁聚焦原理图解
条件:圆形磁场区域半径与粒子轨道半径一样
O1
O2
A
B
磁聚焦原理图解
条件:圆形磁场区域半径与粒子轨道半径一样
O1
O2
A
B
例1.(2009年浙江卷)如图,在xOy平面内与y轴平行的匀强电场,在半径为R的圆内还有与xOy平面垂直的匀强磁场。在圆的左边放置一带电微粒发射装置,它沿x轴正方向发射出一束具有相同质量m、电荷量q(q>0)和初速度v的带电微粒。发射时,这束带电微粒分布在0<y<2R的区间内。已知重力加速度大小为g。
(1)从A点射出的带电微粒平行于x轴从C点进入有磁场区域,并从坐标原点O沿y轴负方向离 开,求电场强度和磁感应强度的大 小与方向。
(2)请指出这束带电微粒与x 轴相交的区域,并说明理由。
x
y
R
O/
O
v
带点微粒发射装置
C
P
Q
r
图 (c)
x
y
R
O/
O
v
C
A
x
y
R
O/
v
Q
P
O
R
θ
图(a)
图(b)
【答案】(1) ;方向垂直于纸面向外 (2)见解析 (3) 与x轴相交的区域范围是x>0.
【解析】 略
【关键】 图示
变式:
如图所示,圆心O1的坐标为(0﹑R),半径为R的圆形区域内存在垂直纸面向里的磁感应强度为B的匀强磁场,在坐标原点O处有一粒子源,可向y>0的区域各个方向发射质量为m电量为-q速度为 的粒子,证明:粒子经过该磁场偏转后都能平行于x轴方向运动。
x
y
O
v0
例2:在xoy平面内有很多质量为m,电量为e的电子,从坐标原点O不断以相同速率沿不同方向射入第一象限,如图所示.现加一垂直于xOy平面向里、磁感强度为B的匀强磁场,要求这些入射电子穿过磁场都能平行于x轴且沿x轴正向运动,试问符合该条件的磁场的最小面积为多大?(不考虑电子间的相互作用)
x
y
O
v0
例2:在xoy平面内有很多质量为m,电量为e的电子,从坐标原点O不断以相同速率沿不同方向射入第一象限,如图所示.现加一垂直于xOy平面向里、磁感强度为B的匀强磁场,要求这些入射电子穿过磁场都能平行于x轴且沿x轴正向运动,试问符合该条件的磁场的最小面积为多大?(不考虑电子间的相互作用)
x
y
O
v0
O1
O2
O3
O4
O5
On
x
y
O
v0
例2:在xoy平面内有很多质量为m,电量为e的电子,从坐标原点O不断以相同速率沿不同方向射入第一象限,如图所示.现加一垂直于xOy平面向里、磁感强度为B的匀强磁场,要求这些入射电子穿过磁场都能平行于x轴且沿x轴正向运动,试问符合该条件的磁场的最小面积为多大?(不考虑电子间的相互作用)
x
y
O
v0
O1
O2
O3
O4
O5
On
例2.(2009·海南·T16)如图,ABCD是边长为a的正方形。质量为m电荷量为e的电子以大小为v0的初速度沿纸面垂直于BC边射入正方形区域。在正方形内适当区域中有匀强磁场,电子从BC边上的任意点入射,都只能从A点射出磁场。不计重力。求:
(1)此匀强磁场区域中磁感应强度的大小和方向;
(2)此匀强磁场区域的最小面积。
A
B
C
D
A
B
C
D
x
y
O
v0
A
B
C
D
x
y
O
v0
S=2(πa2/4-a2/2) =(π-2)a2/2
练习1: 如图所示,纸面内有宽为L水平向 右飞行的带电粒子流,粒子质量为m,电 荷量为-q,速率为v0,不考虑粒子的重力 及相互间的作用,要使粒子都汇聚到一点, 可以在粒子流的右侧虚线框内设计一匀强 磁场区域,则磁场区域的形状及对应的磁 感应强度可以是(其中B0=mv0/qL,A、C、 D选项中曲线均为半径是L的圆弧, B选项中曲线为半径是0.5L的圆)( )
练习2:如图所示,在坐标系xOy内有一半径为a的圆形区域,圆心坐标为O1(a,0),圆内分布有垂直纸面向里的匀强磁场。在直线y=a的上方和直线x=2a的左侧区域内,有一沿y轴负方向的匀强电场,场强大小为E。一质量为m、电荷量为+q(q>0)的粒子以速度v从O点垂直于磁场方向射入,当速度方向沿x轴正方向时,粒子恰好从O1点正上方的A点射出磁场,不计粒子重力。
(1) 求磁感应强度B的大小;
(2) 若粒子以速度v从O点垂直于磁场方向 射入第一象限,当速度方向沿x轴正方向的 夹角为30°时,粒子从射入磁场到最终离开 磁场的时间 t。
