2021-2022学年冀教版八年级数学上册第十七章特殊三角形复习课件(共22张ppt)
文档属性
| 名称 | 2021-2022学年冀教版八年级数学上册第十七章特殊三角形复习课件(共22张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 345.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-03 08:39:40 | ||
图片预览





文档简介
(共22张PPT)
特殊三角形复习
1. 等腰三角形
1. 什么是等腰三角形
有两边相等的三角形叫做等腰三角形
练1已知等腰三角形的两边长分别是4和6,
则它的周长是 .
练2已知等腰三角形的两边长分别是3和6,
则它的周长是 .
14或16
15
一. 知识回顾
小结:在等腰三角形中要注意对边的分类讨论
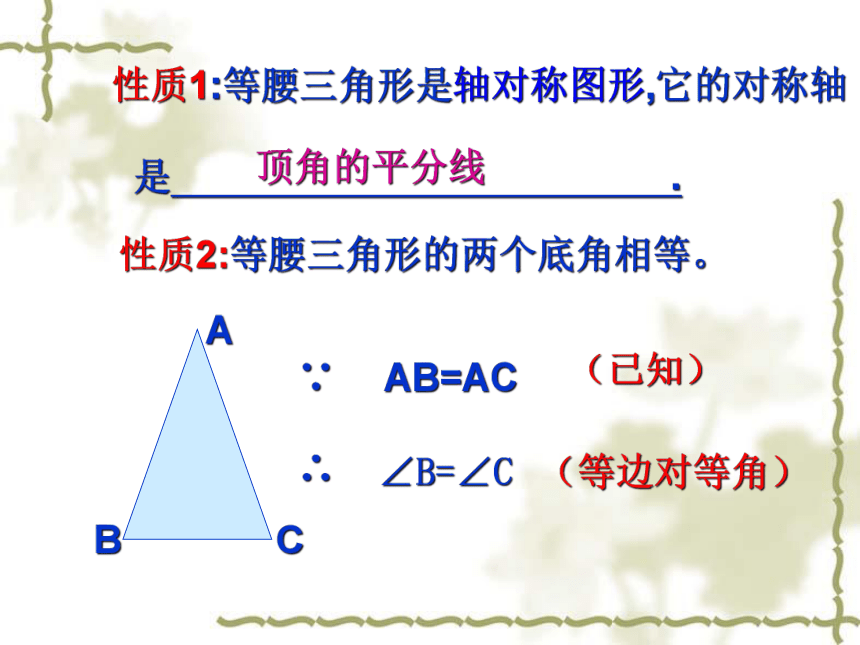
性质1:等腰三角形是轴对称图形,它的对称轴
是 .
性质2:等腰三角形的两个底角相等。
A
C
B
∵
∴
AB=AC
∠B=∠C
(等边对等角)
(已知)
顶角的平分线
练3:已知等腰三角形的一个底角是300,
则它的顶角是 .
练4:已知等腰三角形的一个角是300,
则它的顶角是 .
练5:已知等腰三角形的一个角是1300,
则它的顶角是 .
1200
1200或300
1300
小结:等腰三角形中对角的分类讨论
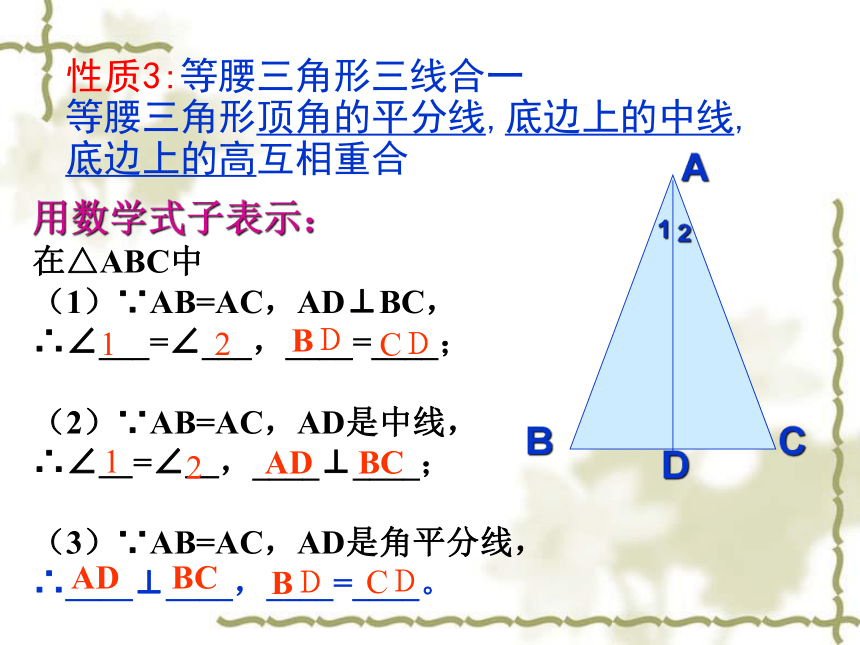
性质3:等腰三角形三线合一
等腰三角形顶角的平分线,底边上的中线,
底边上的高互相重合
在△ABC中
(1)∵AB=AC,AD⊥BC,
∴∠___=∠___,____=____;
(2)∵AB=AC,AD是中线,
∴∠_=∠_,____⊥____;
(3)∵AB=AC,AD是角平分线,
∴____⊥____,____=____。
用数学式子表示:
A
C
B
D
1
2
1
2
BD
CD
1
2
AD
BC
AD
BC
BD
CD
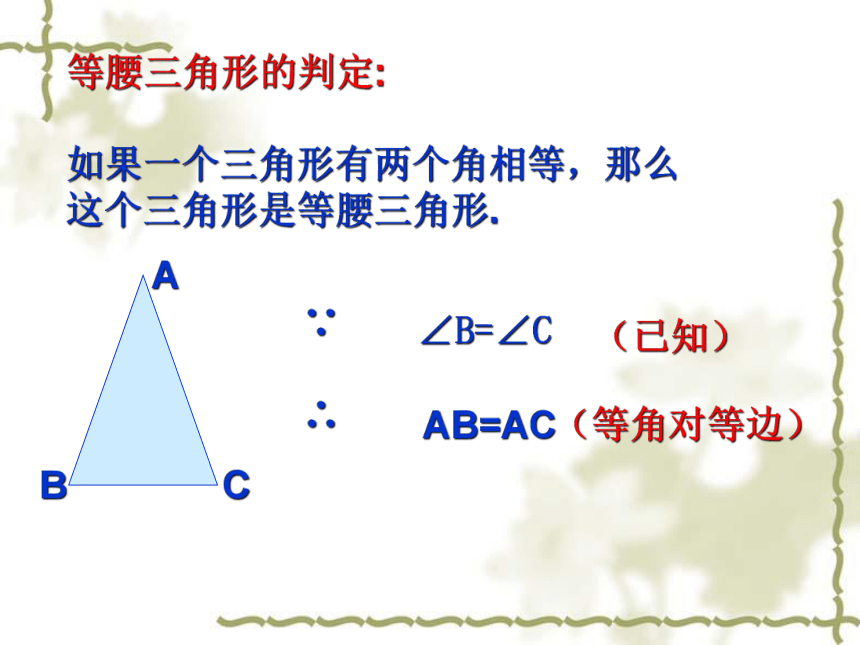
A
C
B
∵
∴
AB=AC
∠B=∠C
(等角对等边)
(已知)
等腰三角形的判定:
如果一个三角形有两个角相等,那么这个三角形是等腰三角形.
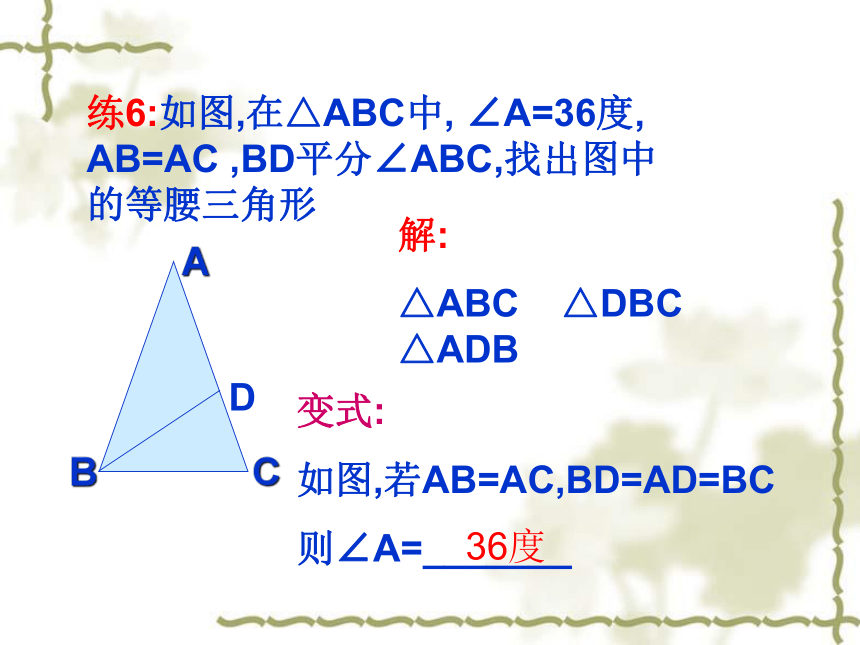
练6:如图,在△ABC中, ∠A=36度, AB=AC ,BD平分∠ABC,找出图中的等腰三角形
A
C
B
D
解:
△ABC △DBC △ADB
变式:
如图,若AB=AC,BD=AD=BC
则∠A=_______
36度
5. 三边都相等的三角形叫做等边三角形
也叫正三角形
等边三角形是特殊的等腰三角形
6.等边三角形的性质:
a. 三边相等
b.三个角相等,都是600
c.三线合一
d.轴对称图形,三条对称轴
7、等边三角形的判定:
(1)三边相等的三角形是等边三角形。
(2)三个角都相等的三角形是等边三角形。
(3)有一个角是600的等腰三角形是等边三角形。
练8:如图,在等边△ABC中,AF=BD=CE,
请说明△DEF也是等边三角形的理由.
解:∵△ABC是等边三角形
∴AC=BC,∠A=∠C
∵CE=BD
∴BC-BC=AC-CE
∴CD=AE
在△AEF和△CDE中
∴△AEF≌△CDE(SAS)
∴EF=DE
同理可证EF=DF
∴EF=DE=DF
∴△DEF是等边三角形
例1:
O是△ABC中∠ABC和∠ACB的平分线的交点,OD∥AB交BC于D,OE∥AC交BC于E点,若BC=10cm,那么△ODE的周长为 。
E
D
O
A
B
C
变式1:
已知:如图,点D、E在△ABC的边BC上,AB=AC,AD=AE,你能判断出BD与CE相等吗?请说出你判断的理由。
F
解: BD=CE。
作AF⊥BC于F,则AF⊥DE
∵AB=AC,AD=AE(已知)
AF⊥BC,AF⊥DE(辅助线作法)
∴BF=CF,DF=EF(等腰三角形底边上的高与底边上的中线互相重合)
∴BD=CE。
变式2:
已知:如图,B、C、 D 、 E都在边BC上,FD、EG分别是AB、AC的中垂线。
1)若BC=10, 求三角形ADE的周长?
2)若∠BAC=100°,求∠DAE的度数。
F
D
E
C
B
A
G
变式1、如图,在等腰△ABC中,AB=AC,若D为BC的中点,DE⊥AB于E,DF⊥AC于F,则DE=DF吗?请说明理由。
解:连结AD
∵在等腰△ ABC中,AB=AC,
D为BC的中点
∴AD是∠BAC的平分线
(等腰三角形三线合一)
又∵ DE⊥AB于E,DF⊥AC于F
∴ DE=DF(角平分线上的点到角两边的距离相等。)
常见的辅助线:等腰三角形三线合一
注意
2.直角三角形
直角三角形的性质:
直角三角形的两个锐角互余
知识回顾
在直角三角形中,30 角所对的直角边等于斜边的一半
直角三角形斜边上的中线等于斜边的一半
勾股定理:直角三角形两直角边的平方和等于斜边的平方
△ADC≌△ADE
∠1=∠2; ∠3=∠4=∠C=90°;∠5=∠6;
AE=AC;DE=CD
你知道多少
线段AD所在的直线
(2)图中有哪些相等的角和相等的线段?
(3)对称轴是哪条线段所在的直线?
(1)你能找出图中全等的三角形吗?
如图操作,折叠直角三角形纸片中,使点C落在AB上的点E处,折痕为AD
归纳(填空):
折叠问题的本质是图形的 变换。
利用轴对称变换得到对应的 相等和对应的
相等
轴对称
角
线段
实质
1.折叠重合部分一定全等(线段、角相等)
2.互相重合的点(对称点)之间的连线必被折痕垂直平分
3.折痕上任意一点与对称两点连接所得的两条线段相等
折叠问题
轴对称
例1:如图,折叠直角三角形纸片,使点C落在AB上的点E处.已知∠B=30°,∠C=90°,
则∠1= ,∠5= .
中考归类一:求角的度数
解:∵△ADE由△ADC折叠而来
∴∠1=∠2,∠3=∠C=90°
在RT△ ABC中
∵∠B=30°, ∠C=90°
∴∠BAC+∠B=90° (为什么?)
∴∠BAC=90°-∠B=90°-30°=60°
∴∠1=∠2= 60 ÷ 2=30°
在RT△AED中∵∠1+ ∠5=90°
∴∠5=90°- 30 °= 60°
30°
60°
如图,CD是Rt△ABC斜边上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于( )
A 25° B 30° C 45° D 60°
体会感悟:
B
例2:如图,折叠直角三角形纸片,使点C落在AB上的点E处.已知BC=12,∠B=30°,∠C=90°,则DE的长是( )
A 6 B 4 C 3 D 2
归类二:求线段的长度
解:∵折叠,
∴ ∠C=∠AED=90°,DE=DC,
设 DE=DC=x
在RT △ BED中
∵∠B=30°,
∴BD=2DE=2x
设未知数 → 方程思想
B
∵BC=12, ∴ BD+CD=12
即2x+x=12,
∴x=4
即DE=4.
x
x
2x
例3.如图,在△ABC中,AB=3,AC=4,BC=5,现将它折叠,使点C与点B重合,求CD的长。
3
5
4-x
x
x
解:∵AB=3,AC=4,BC=5
∵折叠∴CD=BD
设CD=BD=x,则AD=4-x
由勾股定理得:
解得x=
∴CD的长为
4
数形结合思想+方程思想
∴AB +AC =3 +4 =25,BC =5 =25
∴ AB +AC =BC
∴ △ABC为直角三角形,其中∠A=90°
特殊三角形复习
1. 等腰三角形
1. 什么是等腰三角形
有两边相等的三角形叫做等腰三角形
练1已知等腰三角形的两边长分别是4和6,
则它的周长是 .
练2已知等腰三角形的两边长分别是3和6,
则它的周长是 .
14或16
15
一. 知识回顾
小结:在等腰三角形中要注意对边的分类讨论
性质1:等腰三角形是轴对称图形,它的对称轴
是 .
性质2:等腰三角形的两个底角相等。
A
C
B
∵
∴
AB=AC
∠B=∠C
(等边对等角)
(已知)
顶角的平分线
练3:已知等腰三角形的一个底角是300,
则它的顶角是 .
练4:已知等腰三角形的一个角是300,
则它的顶角是 .
练5:已知等腰三角形的一个角是1300,
则它的顶角是 .
1200
1200或300
1300
小结:等腰三角形中对角的分类讨论
性质3:等腰三角形三线合一
等腰三角形顶角的平分线,底边上的中线,
底边上的高互相重合
在△ABC中
(1)∵AB=AC,AD⊥BC,
∴∠___=∠___,____=____;
(2)∵AB=AC,AD是中线,
∴∠_=∠_,____⊥____;
(3)∵AB=AC,AD是角平分线,
∴____⊥____,____=____。
用数学式子表示:
A
C
B
D
1
2
1
2
BD
CD
1
2
AD
BC
AD
BC
BD
CD
A
C
B
∵
∴
AB=AC
∠B=∠C
(等角对等边)
(已知)
等腰三角形的判定:
如果一个三角形有两个角相等,那么这个三角形是等腰三角形.
练6:如图,在△ABC中, ∠A=36度, AB=AC ,BD平分∠ABC,找出图中的等腰三角形
A
C
B
D
解:
△ABC △DBC △ADB
变式:
如图,若AB=AC,BD=AD=BC
则∠A=_______
36度
5. 三边都相等的三角形叫做等边三角形
也叫正三角形
等边三角形是特殊的等腰三角形
6.等边三角形的性质:
a. 三边相等
b.三个角相等,都是600
c.三线合一
d.轴对称图形,三条对称轴
7、等边三角形的判定:
(1)三边相等的三角形是等边三角形。
(2)三个角都相等的三角形是等边三角形。
(3)有一个角是600的等腰三角形是等边三角形。
练8:如图,在等边△ABC中,AF=BD=CE,
请说明△DEF也是等边三角形的理由.
解:∵△ABC是等边三角形
∴AC=BC,∠A=∠C
∵CE=BD
∴BC-BC=AC-CE
∴CD=AE
在△AEF和△CDE中
∴△AEF≌△CDE(SAS)
∴EF=DE
同理可证EF=DF
∴EF=DE=DF
∴△DEF是等边三角形
例1:
O是△ABC中∠ABC和∠ACB的平分线的交点,OD∥AB交BC于D,OE∥AC交BC于E点,若BC=10cm,那么△ODE的周长为 。
E
D
O
A
B
C
变式1:
已知:如图,点D、E在△ABC的边BC上,AB=AC,AD=AE,你能判断出BD与CE相等吗?请说出你判断的理由。
F
解: BD=CE。
作AF⊥BC于F,则AF⊥DE
∵AB=AC,AD=AE(已知)
AF⊥BC,AF⊥DE(辅助线作法)
∴BF=CF,DF=EF(等腰三角形底边上的高与底边上的中线互相重合)
∴BD=CE。
变式2:
已知:如图,B、C、 D 、 E都在边BC上,FD、EG分别是AB、AC的中垂线。
1)若BC=10, 求三角形ADE的周长?
2)若∠BAC=100°,求∠DAE的度数。
F
D
E
C
B
A
G
变式1、如图,在等腰△ABC中,AB=AC,若D为BC的中点,DE⊥AB于E,DF⊥AC于F,则DE=DF吗?请说明理由。
解:连结AD
∵在等腰△ ABC中,AB=AC,
D为BC的中点
∴AD是∠BAC的平分线
(等腰三角形三线合一)
又∵ DE⊥AB于E,DF⊥AC于F
∴ DE=DF(角平分线上的点到角两边的距离相等。)
常见的辅助线:等腰三角形三线合一
注意
2.直角三角形
直角三角形的性质:
直角三角形的两个锐角互余
知识回顾
在直角三角形中,30 角所对的直角边等于斜边的一半
直角三角形斜边上的中线等于斜边的一半
勾股定理:直角三角形两直角边的平方和等于斜边的平方
△ADC≌△ADE
∠1=∠2; ∠3=∠4=∠C=90°;∠5=∠6;
AE=AC;DE=CD
你知道多少
线段AD所在的直线
(2)图中有哪些相等的角和相等的线段?
(3)对称轴是哪条线段所在的直线?
(1)你能找出图中全等的三角形吗?
如图操作,折叠直角三角形纸片中,使点C落在AB上的点E处,折痕为AD
归纳(填空):
折叠问题的本质是图形的 变换。
利用轴对称变换得到对应的 相等和对应的
相等
轴对称
角
线段
实质
1.折叠重合部分一定全等(线段、角相等)
2.互相重合的点(对称点)之间的连线必被折痕垂直平分
3.折痕上任意一点与对称两点连接所得的两条线段相等
折叠问题
轴对称
例1:如图,折叠直角三角形纸片,使点C落在AB上的点E处.已知∠B=30°,∠C=90°,
则∠1= ,∠5= .
中考归类一:求角的度数
解:∵△ADE由△ADC折叠而来
∴∠1=∠2,∠3=∠C=90°
在RT△ ABC中
∵∠B=30°, ∠C=90°
∴∠BAC+∠B=90° (为什么?)
∴∠BAC=90°-∠B=90°-30°=60°
∴∠1=∠2= 60 ÷ 2=30°
在RT△AED中∵∠1+ ∠5=90°
∴∠5=90°- 30 °= 60°
30°
60°
如图,CD是Rt△ABC斜边上的高,将△BCD沿CD折叠,B点恰好落在AB的中点E处,则∠A等于( )
A 25° B 30° C 45° D 60°
体会感悟:
B
例2:如图,折叠直角三角形纸片,使点C落在AB上的点E处.已知BC=12,∠B=30°,∠C=90°,则DE的长是( )
A 6 B 4 C 3 D 2
归类二:求线段的长度
解:∵折叠,
∴ ∠C=∠AED=90°,DE=DC,
设 DE=DC=x
在RT △ BED中
∵∠B=30°,
∴BD=2DE=2x
设未知数 → 方程思想
B
∵BC=12, ∴ BD+CD=12
即2x+x=12,
∴x=4
即DE=4.
x
x
2x
例3.如图,在△ABC中,AB=3,AC=4,BC=5,现将它折叠,使点C与点B重合,求CD的长。
3
5
4-x
x
x
解:∵AB=3,AC=4,BC=5
∵折叠∴CD=BD
设CD=BD=x,则AD=4-x
由勾股定理得:
解得x=
∴CD的长为
4
数形结合思想+方程思想
∴AB +AC =3 +4 =25,BC =5 =25
∴ AB +AC =BC
∴ △ABC为直角三角形,其中∠A=90°
同课章节目录
- 第十二章 分式和分式方程
- 12.1 分式
- 12.2 分式的乘除
- 12.3 分式的加减
- 12.4 分式方程
- 12.5 分式方程的应用
- 第十三章 全等三角形
- 13.1 命题与证明
- 13.2 全等图形
- 13.3 全等三角形的判定
- 13.4 三角形的尺规作图
- 第十四章 实数
- 14.1 平方根
- 14.2 立方根
- 14.3 实数
- 14.4 近似数
- 14.5 用计算器求平方根与立方根
- 第十五章 二次根式
- 15.1 二次根式
- 15.2 二次根式的乘除
- 15.3 二次根式的加减
- 15.4 二次根式的混合
- 第十六章 轴对称和中心对称
- 16.1 轴对称
- 16.2 线段的垂直平分
- 16.3 角的平分线
- 16.4 中心对称图形
- 16.5 利用图形的平移、旋转和轴对称设计图案
- 第十七章 特殊三角形
- 17.1 等腰三角形
- 17.2 直角三角形
- 17.3 勾股定理
- 17.4 直角三角形全等的判定
- 17.5 反证法
