新疆维吾尔自治区喀什第六高级中学2021-2022学年高一上学期12月月考数学试题(Word版含答案)
文档属性
| 名称 | 新疆维吾尔自治区喀什第六高级中学2021-2022学年高一上学期12月月考数学试题(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 254.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-03 15:40:49 | ||
图片预览



文档简介
喀什第六高级中学2021-2022学年高一上学期12月月考
数学试题
(时间:120分钟 满分:150分)
一、单选题
1.下列表示错误的是( )
A. B. C. D.
2.2021年7月,某文学网站对该网站的数字媒体内容能否满足读者需要进行了调查,调查部门随机抽取了名读者,所得情况统计如下表所示:
满意程度 学生族 上班族 退休族
满意
一般
不满意
记满分为分,一般为分,不满意为分.设命题:按分层抽样方式从不满意的读者中抽取人,则退休族应抽取人;命题:样本中上班族对数字媒体内容满意程度的方差为.
则下列命题中为真命题的是( )
A. B. C. D.
3.已知函数,则( )
A. B. C. D.
4.抛掷一枚质地均匀且各个面上分别标以数字1,2,3,4,5,6的正方体玩具.设事件A为“向上一面点数为偶数”,事件B为“向上一面点数为6的约数”,则事件“A或B”发生的概率为( )
A. B. C. D.
5.函数f(x)的图象向左平移一个单位长度,所得图象与y=ex关于x轴对称,则f(x)=( )
A.-ex-1 B.-ex+1 C.-e-x-1 D.-e-x+1
6.已知一组数据为20,30,40,50,50,50,70,80,其平均数、第60百分位数和众数的大小关系是( )
A.平均数=第60百分位数>众数 B.平均数<第60百分位数=众数
C.第60百分位数=众数<平均数 D.平均数=第60百分位数=众数
7.下列各组函数是同一函数的是( )
①与.②与.③与.④与.
A.①② B.①③ C.③④ D.①④
8.已知函数f(x)=3x+2cosx,若,b=f(2),c=f(log27),则a,b,c的大小关系是( )
A.aC.b9.已知函数是定义在闭区间上的奇函数,,则的最大值与最小值之和为( )
A.1 B.2 C.3 D.0
10.用符号[x]表示不超过x的最大整数(称为x的整数部分),如[﹣1.2]=﹣2,[0.2]=0,[1]=1,设函数f(x)=(1﹣lnx)(lnx﹣ax)有三个不同的零点x1,x2,x3,若[x1]+[x2]+[x3]=6,则实数a的取值范围是( )
A. B. C. D.
11.函数的值域为( )
A. B. C. D.
12.己知命题;命题是的充要条件则下列为真命题的是( )
A. B. C. D.
二、填空题
13.甲、乙两名学生某门课程的5次测试成绩依次分别为60,80,70,90,70和80,65,70,80,75,因为________,所以学生________成绩更稳定.
14.用二分法求函数的一个零点,其参考数据如下:
据此数据,可知的一个零点的近似值可取为______(误差不超过0.005).
15.函数在上是减函数,则实数的范围是_______.
16.若一个集合是另一个集合的子集,则称两个集合构成“鲸吞”;若两个集合有公共元素,且互不为对方子集,则称两个集合构成“蚕食”,对于集合,,若这两个集合构成“鲸吞”或“蚕食”,则a的取值集合为_____.
四、解答题(共70分)
17.(本题10分)设函数且是定义域为的奇函数;
(1)若,判断的单调性并求不等式的解集;
(2)若,且,求在上的最小值.
18.(本题12分)已知集合,.
(1)若,求的取值范围;
(2)若,求的取值范围.
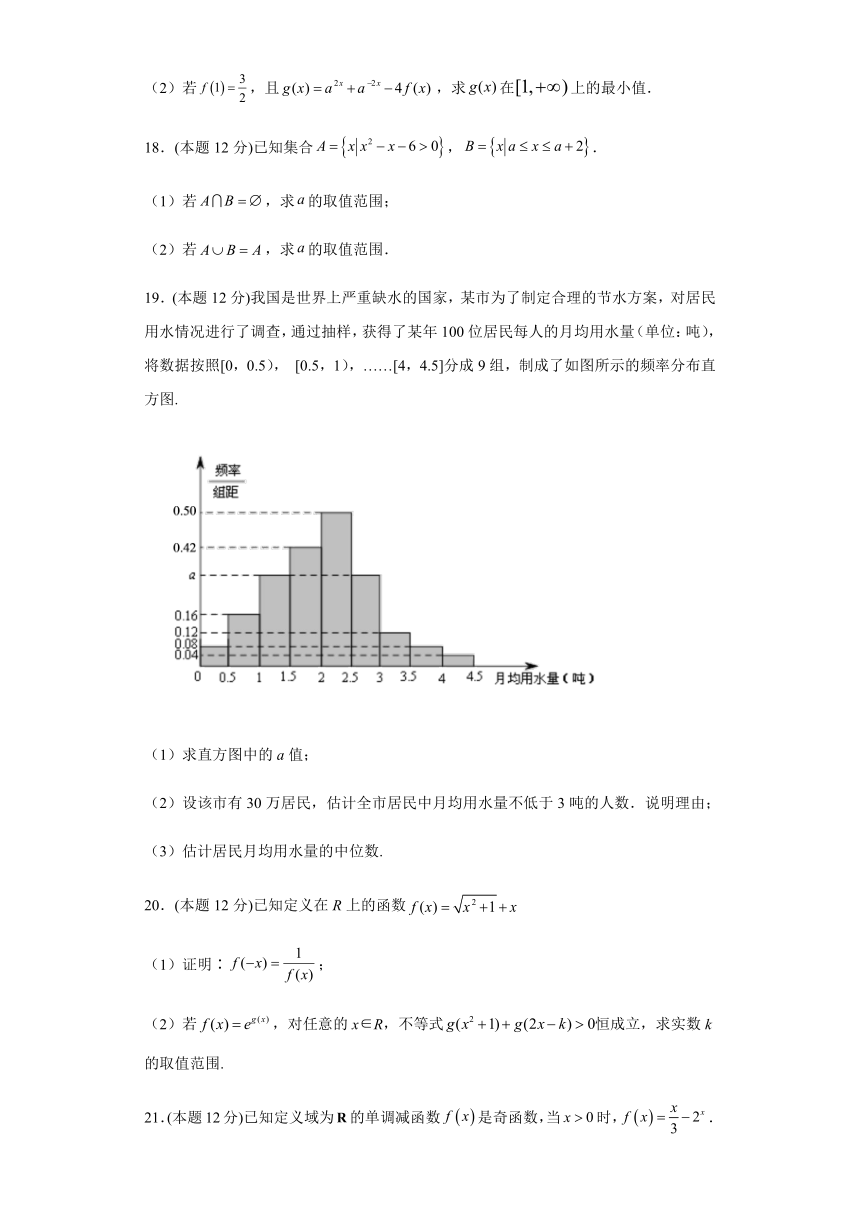
19.(本题12分)我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5), [0.5,1),……[4,4.5]分成9组,制成了如图所示的频率分布直方图.
(1)求直方图中的a值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数.说明理由;
(3)估计居民月均用水量的中位数.
20.(本题12分)已知定义在R上的函数
(1)证明∶;
(2)若,对任意的x∈R,不等式恒成立,求实数k的取值范围.
21.(本题12分)已知定义域为的单调减函数是奇函数,当时,.
(1)求的解析式;
(2)若任意,不等式恒成立,求实数的取值范围.
22.(本题12分)已知函数,其中.
(1)当时,写出单调区间,并求的最小值;
(2)若函数在区间上是减函数,求实数的取值范围;
(3)求关于的不等式的解集.
参考答案
1.A
2.A
3.A
4.D
5.A
6.B
7.C
8.D
9.B
10.B
11.C
12.C
13. 乙
14.1.55935(答案不唯一)
15.
16.
17.(1)增函数,;(2).
18.
(1)
(2)
19.
(1)
(2)36000,理由见解析
(3)2.04
20.
(1)证明见解析
(2)
21.
(1)
(2)
22.
(1)单调递增区间;单调递减区间;最小值
(2)
(3)答案不唯一,具体见解析
数学试题
(时间:120分钟 满分:150分)
一、单选题
1.下列表示错误的是( )
A. B. C. D.
2.2021年7月,某文学网站对该网站的数字媒体内容能否满足读者需要进行了调查,调查部门随机抽取了名读者,所得情况统计如下表所示:
满意程度 学生族 上班族 退休族
满意
一般
不满意
记满分为分,一般为分,不满意为分.设命题:按分层抽样方式从不满意的读者中抽取人,则退休族应抽取人;命题:样本中上班族对数字媒体内容满意程度的方差为.
则下列命题中为真命题的是( )
A. B. C. D.
3.已知函数,则( )
A. B. C. D.
4.抛掷一枚质地均匀且各个面上分别标以数字1,2,3,4,5,6的正方体玩具.设事件A为“向上一面点数为偶数”,事件B为“向上一面点数为6的约数”,则事件“A或B”发生的概率为( )
A. B. C. D.
5.函数f(x)的图象向左平移一个单位长度,所得图象与y=ex关于x轴对称,则f(x)=( )
A.-ex-1 B.-ex+1 C.-e-x-1 D.-e-x+1
6.已知一组数据为20,30,40,50,50,50,70,80,其平均数、第60百分位数和众数的大小关系是( )
A.平均数=第60百分位数>众数 B.平均数<第60百分位数=众数
C.第60百分位数=众数<平均数 D.平均数=第60百分位数=众数
7.下列各组函数是同一函数的是( )
①与.②与.③与.④与.
A.①② B.①③ C.③④ D.①④
8.已知函数f(x)=3x+2cosx,若,b=f(2),c=f(log27),则a,b,c的大小关系是( )
A.a
A.1 B.2 C.3 D.0
10.用符号[x]表示不超过x的最大整数(称为x的整数部分),如[﹣1.2]=﹣2,[0.2]=0,[1]=1,设函数f(x)=(1﹣lnx)(lnx﹣ax)有三个不同的零点x1,x2,x3,若[x1]+[x2]+[x3]=6,则实数a的取值范围是( )
A. B. C. D.
11.函数的值域为( )
A. B. C. D.
12.己知命题;命题是的充要条件则下列为真命题的是( )
A. B. C. D.
二、填空题
13.甲、乙两名学生某门课程的5次测试成绩依次分别为60,80,70,90,70和80,65,70,80,75,因为________,所以学生________成绩更稳定.
14.用二分法求函数的一个零点,其参考数据如下:
据此数据,可知的一个零点的近似值可取为______(误差不超过0.005).
15.函数在上是减函数,则实数的范围是_______.
16.若一个集合是另一个集合的子集,则称两个集合构成“鲸吞”;若两个集合有公共元素,且互不为对方子集,则称两个集合构成“蚕食”,对于集合,,若这两个集合构成“鲸吞”或“蚕食”,则a的取值集合为_____.
四、解答题(共70分)
17.(本题10分)设函数且是定义域为的奇函数;
(1)若,判断的单调性并求不等式的解集;
(2)若,且,求在上的最小值.
18.(本题12分)已知集合,.
(1)若,求的取值范围;
(2)若,求的取值范围.
19.(本题12分)我国是世界上严重缺水的国家,某市为了制定合理的节水方案,对居民用水情况进行了调查,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照[0,0.5), [0.5,1),……[4,4.5]分成9组,制成了如图所示的频率分布直方图.
(1)求直方图中的a值;
(2)设该市有30万居民,估计全市居民中月均用水量不低于3吨的人数.说明理由;
(3)估计居民月均用水量的中位数.
20.(本题12分)已知定义在R上的函数
(1)证明∶;
(2)若,对任意的x∈R,不等式恒成立,求实数k的取值范围.
21.(本题12分)已知定义域为的单调减函数是奇函数,当时,.
(1)求的解析式;
(2)若任意,不等式恒成立,求实数的取值范围.
22.(本题12分)已知函数,其中.
(1)当时,写出单调区间,并求的最小值;
(2)若函数在区间上是减函数,求实数的取值范围;
(3)求关于的不等式的解集.
参考答案
1.A
2.A
3.A
4.D
5.A
6.B
7.C
8.D
9.B
10.B
11.C
12.C
13. 乙
14.1.55935(答案不唯一)
15.
16.
17.(1)增函数,;(2).
18.
(1)
(2)
19.
(1)
(2)36000,理由见解析
(3)2.04
20.
(1)证明见解析
(2)
21.
(1)
(2)
22.
(1)单调递增区间;单调递减区间;最小值
(2)
(3)答案不唯一,具体见解析
同课章节目录
