黑龙江省大庆市龙凤区2021-2022学年七年级(五四学制)上学期期末考试数学试题(word版含答案)
文档属性
| 名称 | 黑龙江省大庆市龙凤区2021-2022学年七年级(五四学制)上学期期末考试数学试题(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 277.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-03 00:00:00 | ||
图片预览




文档简介
龙凤区2021-2022学年第一学期期末考试 七年级
数 学 试 题
姓名: 班级: 考号:
一、选择题(每题3分共30分)
1.下列运算正确的是( )
A.a2 a3=a6 B.3a﹣a=3 C.(b3)2=b9 D.x6÷x2=x4
2.下列手机软件图标中,是轴对称图形的是( )
A. B. C. D.
3.下列事件为必然事件的是( )
A.小王参加本次数学考试,成绩是500分
B.某射击运动员射靶一次,正中靶心
C.打开电视机,CCTV第一套节目正在播放新闻
D.口袋中装有2个红球和1个白球,从中摸出2个球,其中必有红球
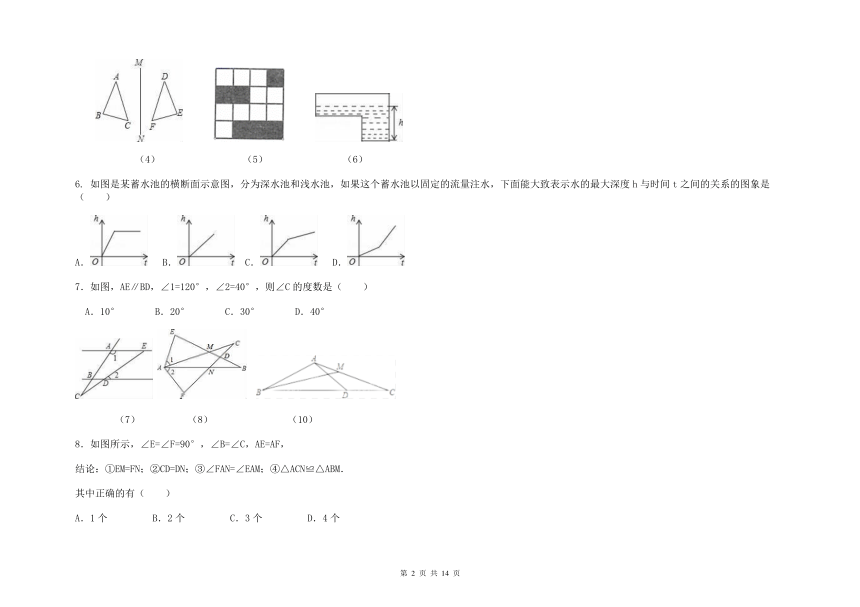
4.如图,△ABC与△DEF关于直线MN轴对称,则以下结论中错误的是( )
AB∥DF B.∠B=∠E C.AB=DE D.AD的连线被MN垂直平分
5. 如图,一枚飞镖游戏板由大小相等的小正方形格子构成.向游戏板随机投掷一枚飞镖,击中黑色区域的概率是( )
A. B. C. D.
(5) (6)
6. 如图是某蓄水池的横断面示意图,分为深水池和浅水池,如果这个蓄水池以固定的流量注水,下面能大致表示水的最大深度h与时间t之间的关系的图象是( )
A. B. C. D.
7.如图,AE∥BD,∠1=120°,∠2=40°,则∠C的度数是( )
A.10° B.20° C.30° D.40°
(8) (10)
如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,
结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN≌△ABM.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
9.已知(x-2 015)2+(x-2 017)2=34,则(x-2 016)2的值是( )
A.4 B.8 C.12 D.16
10.如图,BM是△ABC的角平分线,D是BC边上的一点,连接AD,使AD=DC,且∠BAD=120°,则∠AMB=( )
A.30° B.25° C.22.5° D.20°
二.填空题(每题3分共24分 )
11.将0.0000025用科学记数法表示为
12.一个长方体的底面是一个边长为10cm的正方形,如果高为h(cm)时,体积为V(cm3),则V与h的关系为___________________;
13. 如图,已知,,,则__________.
(14) (15) (18)
14.在等腰△ABC中,AB=AC,AC腰上的中线BD将三角形周长分为15和21两部分,则这个三角形的底边长为 .
15.如图已知,和的平分线相交于,,求的度数 .
16. 已如一个口袋中装有7个只有颜色不同的球,其中3个白球,4个黑球.
若往口袋中再放入2个白球,求从口袋中随机取出一个白球的概率
17.如果3a=5,3b=10,那么9a-b的值为
18.已知:四边形ABCD中,AB=AD=CD,∠BAD=90°,三角形ABC的面积为1,则线段AC的长度是 .
三.解答题
计算(6分)
(1) (2x5)2-(-3x3)·2x7 (2) (-1) 2019+ (-) -2+ (3.14- π)0
20.(6分) 先化简,再求值:(a﹣2b)(a+2b)﹣(a﹣2b)2+8b2,
其中a=﹣6,b=
21.(6分)暑假将至,某商场为了吸引顾客,设计了可以自由转动的转盘(如图所示,转盘被均匀地分为20份),并规定:顾客每 200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.若某顾客购物300元.
(1)求他此时获得购物券的概率是多少?(3分)
(2)他获得哪种购物券的概率最大?请说明理由.(3分)
22.(6分)如图,AB∥CD,∠BMN与∠DNM的平分线相交于点G,
完成下面的证明:
∵ MG平分∠BMN,
∴ ∠GMN=∠BMN( ),
同理∠GNM=∠DNM.
∵ AB∥CD
∴ ∠BMN+∠DNM=________( ).
∴ ∠GMN+∠GNM=________.
∵ ∠GMN+∠GNM+∠G=________,
∴ ∠G= ________.
23、(6分)如图,已知AB=AC,BD=CE,证明△ABE≌△ACD.
24.(7分)在△ABC中,AB=AC, ∠A=120°,AB的垂直平分线交BC于M,交AB于E,AC的垂直平分线交BC于N,交AC于F,求证:BM=MN=NC.
25.(7分)一农民朋友带了若干千克的土豆进城出售,为了方便,他带了一些零钱备用.按市场售出一些后,又降价出售.售出土豆千克数x与他手中持有的钱数y(含备用零钱)的关系, 如图所示,结合图像回答下列问题:
(1)农民自带的零钱是多少?
(2)降价前他每千克土豆出售的价格是多少?
(3)降价后他按每千克0.4元将剩余的土豆售完,这时他手中
的钱(含备用的钱)是26元,问他一共带了多少千克的土豆?
26.(8分)已知:如图1,点A是线段DE上一点,∠BAC=90°,AB=AC,BD⊥DE,CE⊥DE,
(1)求证:DE=BD+CE.
(2)如图2,我们能得到关于DE、BD、CE数量关系的结论?并证明.
27.(7分)算式.计算的结果个位是几?
28.(7分)如图9所示,△ABC是等腰直角三角形,∠ACB=90°,AD是BC边上的中线,过C作AD的垂线,交AB于点E,交AD于点F,求证:∠ADC=∠BDE.
桌号
班级
姓名
考号
龙凤区2021-2022学年第一学期期末考试七年级
数 学 考 试 题 答 案
一、选择题(每题3分共30分)
1 2 3 4 5 6 7 8 9 10
D C D A B C B C D A
二.填空题(每题3分共24分 )
11 12 13 14
2.5×10 V=100h 95° 8或16
15 16 17 18
110° 2
19.计算(6分)
解:(3分)(1)原式为:
=
=;
(2)(3分)原式为:
=
=4.
20.(6分) 先化简,再求值:(a﹣2b)(a+2b)﹣(a﹣2b)2+8b2,
其中a=﹣6,b=
原式=a2﹣4b2﹣a2+4ab﹣4b2+8b2=4ab,(3分)
当a=﹣6,b=时,原式=﹣8.(3分)
21解:(6分)(1)(3分)
∵转盘被均匀地分为20份,他此时获得购物券的有10份,
∴他此时获得购物券的概率是: =;
(2)(3分)
∵P(获得200元购物券)=,P(获得100元购物券)=,P(获得50元购物券)==,
∴他获得50元购物券的概率最大.
22.(每空1分,共6分)
角分线定义
180° 两直线平行同旁内角互补
90°
180°
90°
23、(6分)证明:看过程酌情。
∵AB=AC,BD=CE,
∴AD=AE.----(2分)
又∵∠A=∠A,----(2分)
∴△ABE≌△ACD(SAS).----(2分)
24.(7分)
方法不唯一,酌情。
连接AM、AN,
由AB=AC, ∠A=120°得∠B=∠C=30°--(1分)
EM是AB的垂直平分线
得AM=BM,∠MAE=30°
同理证明AN=CN,∠NAF=30°--(3分)
得∠MAN=60°
利用外角∠AMN=60°
可证△MAN是等边三角形
可证:BM=MN=NC. ---(3分)
25.(7分)
(1)农民自带的零钱是5元(2分)
(2) (20-5)÷30=0.5(元)
答:降价前他每千克土豆出售的价格是每千克0.5元(2分)
(26-20)÷0.4=15(千克)
15+30=45(千克)
(3)答:他一共带了45千克的土豆。(3分)
26.(8分)已知:如图1,点A是线段DE上一点,∠BAC=90°,AB=AC,BD⊥DE,CE⊥DE,
(1)求证:DE=BD+CE.
(2)如图2,我们能得到关于DE、BD、CE数量关系的结论?并证明.
【解答】证明:(4分)(1)∵BD⊥DE,CE⊥DE,
∴∠D=∠E=90°,
∴∠DBA+∠DAB=90°,
∵∠BAC=90°,
∴∠DAB+∠CAE=90°,
∴∠DBA=∠CAE,
∵AB=AC,
∴△ADB≌△CEA,
∴BD=AE,CE=AD,
∴DE=AD+AE=CE+BD;
(2)(4分)BD=DE+CE,理由是:
∵BD⊥DE,CE⊥DE,
∴∠ADB=∠AEC=90°,
∴∠ABD+∠BAD=90°,
∵∠BAC=90°,
∴∠ABD+∠EAC=90°,
∴∠BAD=∠EAC,
∵AB=AC,
∴△ADB≌△CEA,
∴BD=AE,CE=AD,
∵AE=AD+DE,
∴BD=CE+DE.
27.(7分)对于算式.计算的结果个位是几?
利用(3-1)替换2得(3-1)+1=3(4分)
3=3
3=9
3=27
3=81
---------
结果个位是1(3分)
28.(7分)如图9所示,△ABC是等腰直角三角形,∠ACB=90°,AD是BC边上的中线,过C作AD的垂线,交AB于点E,交AD于点F,求证:∠ADC=∠BDE.
28.(7分)如图11所示,过B点作BH⊥BC交CE的延长线于H点.(1分)
∵∠CAD+∠ACF=90°,∠BCH+∠ACF=90°,
∴∠CAD=∠BCH.在△ACD与△CBH中,
∵∠CAD=∠BCH,AC=CB,∠ACD=∠CBH=90°,
∴△ACD≌△CBH.∴∠ADC=∠H ① CD=BH,
∵CD=BD,∴BD=BH.(3分)
∵△ABC是等腰直角三角形,∠CBA=∠HBE=45°
∴在△BED和BEH中,,∴△BED≌△BEH.
∴∠BDE=∠H, ② 由①②得,∠ADC=∠BDE.(3分)
A
C
F
N
M
E
B
y(元)
26
20
10
5
0
x(千克)
30
A
B
C
D
E
F
图9
A
C
F
N
M
E
B
A
B
C
D
E
F
图9
A
B
C
D
E
F
H
图11
数 学 试 题
姓名: 班级: 考号:
一、选择题(每题3分共30分)
1.下列运算正确的是( )
A.a2 a3=a6 B.3a﹣a=3 C.(b3)2=b9 D.x6÷x2=x4
2.下列手机软件图标中,是轴对称图形的是( )
A. B. C. D.
3.下列事件为必然事件的是( )
A.小王参加本次数学考试,成绩是500分
B.某射击运动员射靶一次,正中靶心
C.打开电视机,CCTV第一套节目正在播放新闻
D.口袋中装有2个红球和1个白球,从中摸出2个球,其中必有红球
4.如图,△ABC与△DEF关于直线MN轴对称,则以下结论中错误的是( )
AB∥DF B.∠B=∠E C.AB=DE D.AD的连线被MN垂直平分
5. 如图,一枚飞镖游戏板由大小相等的小正方形格子构成.向游戏板随机投掷一枚飞镖,击中黑色区域的概率是( )
A. B. C. D.
(5) (6)
6. 如图是某蓄水池的横断面示意图,分为深水池和浅水池,如果这个蓄水池以固定的流量注水,下面能大致表示水的最大深度h与时间t之间的关系的图象是( )
A. B. C. D.
7.如图,AE∥BD,∠1=120°,∠2=40°,则∠C的度数是( )
A.10° B.20° C.30° D.40°
(8) (10)
如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,
结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN≌△ABM.
其中正确的有( )
A.1个 B.2个 C.3个 D.4个
9.已知(x-2 015)2+(x-2 017)2=34,则(x-2 016)2的值是( )
A.4 B.8 C.12 D.16
10.如图,BM是△ABC的角平分线,D是BC边上的一点,连接AD,使AD=DC,且∠BAD=120°,则∠AMB=( )
A.30° B.25° C.22.5° D.20°
二.填空题(每题3分共24分 )
11.将0.0000025用科学记数法表示为
12.一个长方体的底面是一个边长为10cm的正方形,如果高为h(cm)时,体积为V(cm3),则V与h的关系为___________________;
13. 如图,已知,,,则__________.
(14) (15) (18)
14.在等腰△ABC中,AB=AC,AC腰上的中线BD将三角形周长分为15和21两部分,则这个三角形的底边长为 .
15.如图已知,和的平分线相交于,,求的度数 .
16. 已如一个口袋中装有7个只有颜色不同的球,其中3个白球,4个黑球.
若往口袋中再放入2个白球,求从口袋中随机取出一个白球的概率
17.如果3a=5,3b=10,那么9a-b的值为
18.已知:四边形ABCD中,AB=AD=CD,∠BAD=90°,三角形ABC的面积为1,则线段AC的长度是 .
三.解答题
计算(6分)
(1) (2x5)2-(-3x3)·2x7 (2) (-1) 2019+ (-) -2+ (3.14- π)0
20.(6分) 先化简,再求值:(a﹣2b)(a+2b)﹣(a﹣2b)2+8b2,
其中a=﹣6,b=
21.(6分)暑假将至,某商场为了吸引顾客,设计了可以自由转动的转盘(如图所示,转盘被均匀地分为20份),并规定:顾客每 200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.若某顾客购物300元.
(1)求他此时获得购物券的概率是多少?(3分)
(2)他获得哪种购物券的概率最大?请说明理由.(3分)
22.(6分)如图,AB∥CD,∠BMN与∠DNM的平分线相交于点G,
完成下面的证明:
∵ MG平分∠BMN,
∴ ∠GMN=∠BMN( ),
同理∠GNM=∠DNM.
∵ AB∥CD
∴ ∠BMN+∠DNM=________( ).
∴ ∠GMN+∠GNM=________.
∵ ∠GMN+∠GNM+∠G=________,
∴ ∠G= ________.
23、(6分)如图,已知AB=AC,BD=CE,证明△ABE≌△ACD.
24.(7分)在△ABC中,AB=AC, ∠A=120°,AB的垂直平分线交BC于M,交AB于E,AC的垂直平分线交BC于N,交AC于F,求证:BM=MN=NC.
25.(7分)一农民朋友带了若干千克的土豆进城出售,为了方便,他带了一些零钱备用.按市场售出一些后,又降价出售.售出土豆千克数x与他手中持有的钱数y(含备用零钱)的关系, 如图所示,结合图像回答下列问题:
(1)农民自带的零钱是多少?
(2)降价前他每千克土豆出售的价格是多少?
(3)降价后他按每千克0.4元将剩余的土豆售完,这时他手中
的钱(含备用的钱)是26元,问他一共带了多少千克的土豆?
26.(8分)已知:如图1,点A是线段DE上一点,∠BAC=90°,AB=AC,BD⊥DE,CE⊥DE,
(1)求证:DE=BD+CE.
(2)如图2,我们能得到关于DE、BD、CE数量关系的结论?并证明.
27.(7分)算式.计算的结果个位是几?
28.(7分)如图9所示,△ABC是等腰直角三角形,∠ACB=90°,AD是BC边上的中线,过C作AD的垂线,交AB于点E,交AD于点F,求证:∠ADC=∠BDE.
桌号
班级
姓名
考号
龙凤区2021-2022学年第一学期期末考试七年级
数 学 考 试 题 答 案
一、选择题(每题3分共30分)
1 2 3 4 5 6 7 8 9 10
D C D A B C B C D A
二.填空题(每题3分共24分 )
11 12 13 14
2.5×10 V=100h 95° 8或16
15 16 17 18
110° 2
19.计算(6分)
解:(3分)(1)原式为:
=
=;
(2)(3分)原式为:
=
=4.
20.(6分) 先化简,再求值:(a﹣2b)(a+2b)﹣(a﹣2b)2+8b2,
其中a=﹣6,b=
原式=a2﹣4b2﹣a2+4ab﹣4b2+8b2=4ab,(3分)
当a=﹣6,b=时,原式=﹣8.(3分)
21解:(6分)(1)(3分)
∵转盘被均匀地分为20份,他此时获得购物券的有10份,
∴他此时获得购物券的概率是: =;
(2)(3分)
∵P(获得200元购物券)=,P(获得100元购物券)=,P(获得50元购物券)==,
∴他获得50元购物券的概率最大.
22.(每空1分,共6分)
角分线定义
180° 两直线平行同旁内角互补
90°
180°
90°
23、(6分)证明:看过程酌情。
∵AB=AC,BD=CE,
∴AD=AE.----(2分)
又∵∠A=∠A,----(2分)
∴△ABE≌△ACD(SAS).----(2分)
24.(7分)
方法不唯一,酌情。
连接AM、AN,
由AB=AC, ∠A=120°得∠B=∠C=30°--(1分)
EM是AB的垂直平分线
得AM=BM,∠MAE=30°
同理证明AN=CN,∠NAF=30°--(3分)
得∠MAN=60°
利用外角∠AMN=60°
可证△MAN是等边三角形
可证:BM=MN=NC. ---(3分)
25.(7分)
(1)农民自带的零钱是5元(2分)
(2) (20-5)÷30=0.5(元)
答:降价前他每千克土豆出售的价格是每千克0.5元(2分)
(26-20)÷0.4=15(千克)
15+30=45(千克)
(3)答:他一共带了45千克的土豆。(3分)
26.(8分)已知:如图1,点A是线段DE上一点,∠BAC=90°,AB=AC,BD⊥DE,CE⊥DE,
(1)求证:DE=BD+CE.
(2)如图2,我们能得到关于DE、BD、CE数量关系的结论?并证明.
【解答】证明:(4分)(1)∵BD⊥DE,CE⊥DE,
∴∠D=∠E=90°,
∴∠DBA+∠DAB=90°,
∵∠BAC=90°,
∴∠DAB+∠CAE=90°,
∴∠DBA=∠CAE,
∵AB=AC,
∴△ADB≌△CEA,
∴BD=AE,CE=AD,
∴DE=AD+AE=CE+BD;
(2)(4分)BD=DE+CE,理由是:
∵BD⊥DE,CE⊥DE,
∴∠ADB=∠AEC=90°,
∴∠ABD+∠BAD=90°,
∵∠BAC=90°,
∴∠ABD+∠EAC=90°,
∴∠BAD=∠EAC,
∵AB=AC,
∴△ADB≌△CEA,
∴BD=AE,CE=AD,
∵AE=AD+DE,
∴BD=CE+DE.
27.(7分)对于算式.计算的结果个位是几?
利用(3-1)替换2得(3-1)+1=3(4分)
3=3
3=9
3=27
3=81
---------
结果个位是1(3分)
28.(7分)如图9所示,△ABC是等腰直角三角形,∠ACB=90°,AD是BC边上的中线,过C作AD的垂线,交AB于点E,交AD于点F,求证:∠ADC=∠BDE.
28.(7分)如图11所示,过B点作BH⊥BC交CE的延长线于H点.(1分)
∵∠CAD+∠ACF=90°,∠BCH+∠ACF=90°,
∴∠CAD=∠BCH.在△ACD与△CBH中,
∵∠CAD=∠BCH,AC=CB,∠ACD=∠CBH=90°,
∴△ACD≌△CBH.∴∠ADC=∠H ① CD=BH,
∵CD=BD,∴BD=BH.(3分)
∵△ABC是等腰直角三角形,∠CBA=∠HBE=45°
∴在△BED和BEH中,,∴△BED≌△BEH.
∴∠BDE=∠H, ② 由①②得,∠ADC=∠BDE.(3分)
A
C
F
N
M
E
B
y(元)
26
20
10
5
0
x(千克)
30
A
B
C
D
E
F
图9
A
C
F
N
M
E
B
A
B
C
D
E
F
图9
A
B
C
D
E
F
H
图11
同课章节目录
