北师大版七年级下册数学3.2用关系式表示的变量间关系课件(共22张ppt)
文档属性
| 名称 | 北师大版七年级下册数学3.2用关系式表示的变量间关系课件(共22张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 466.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-03 09:10:08 | ||
图片预览







文档简介
(共22张PPT)
时间在分分秒秒的流逝,
我们在点点滴滴的进步
汽车行驶路程随行驶时间而变化
聪明的乌鸦认识到:
1、瓶口的大小不可改变,水的量也不可改变;
2、但瓶中水的高度是可以改变的,投的石块越多则水面就越高
情景引入
1kg
2kg
3kg
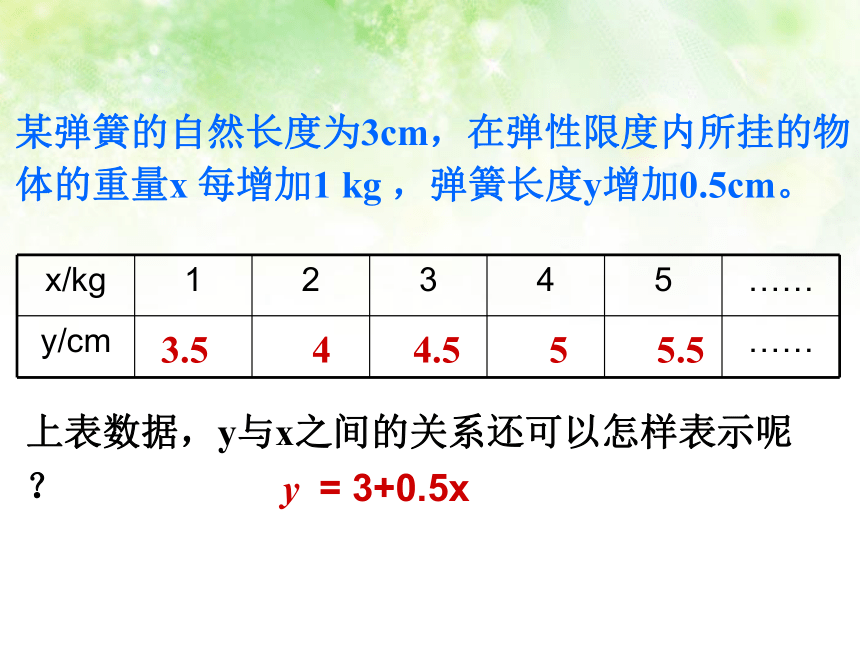
某弹簧的自然长度为3cm,在弹性限度内所挂的物体的重量x 每增加1 kg ,弹簧长度y增加0.5cm。
x/kg 1 2 3 4 5 ……
y/cm ……
上表数据,y与x之间的关系还可以怎样表示呢?
3.5
y = 3+0.5x
4
4.5
5
5.5
§3.2用关系式表示的
变量间关系
北师大版七年级数学下册
第三章 变量之间的关系
自主学习
同学们自主学习课本P66页内容
3、如图所示,梯形上底的长是a ,下底的长是15,
高是8,上底变化时,梯形的面积随之改变。
(1)梯形面积S与上底长a之间的关系式是什么?
(2)当a每增加1时,S如何变化?
(3)当a=0时,S等于什么?此时它表示的什么?
a
8
15
合作探究
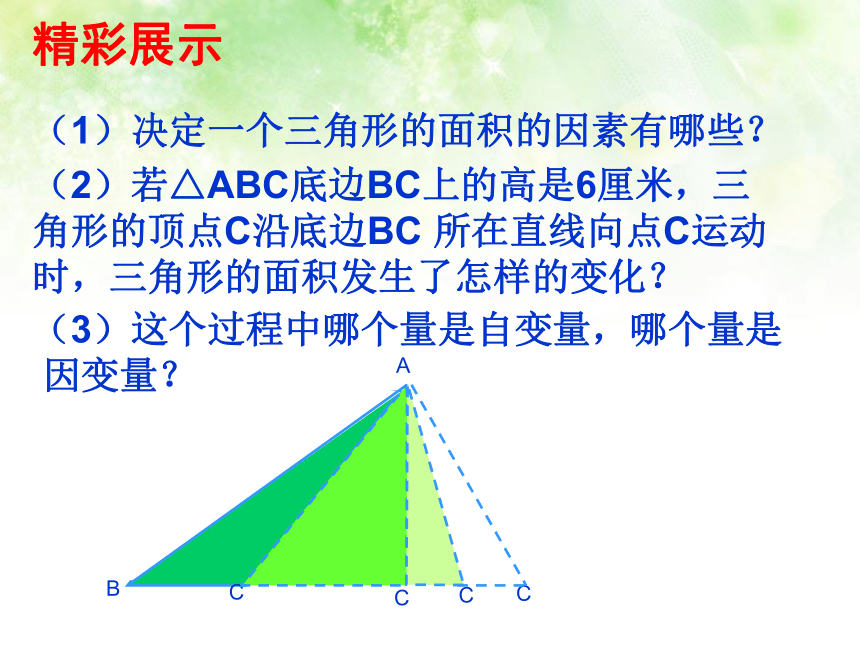
(3)这个过程中哪个量是自变量,哪个量是
因变量?
(1)决定一个三角形的面积的因素有哪些?
(2)若△ABC底边BC上的高是6厘米,三角形的顶点C沿底边BC 所在直线向点C运动时,三角形的面积发生了怎样的变化?
A
C
B
C
C
C
精彩展示
(4)如果三角形的底边长为 x(厘米),那么三角形的面积y(厘米2)可以表示为 ________
y =3x
(5)当底边长从12厘米变化到3厘米时,
三角形的面积从_____厘米2变化
到_____厘米2.
36
9
精彩展示
y=3x表示了 和 之间 的关系,它是变量 随 变化的关系式.
三角形底边长 x
面积 y
3x
含自变量代数式
因变量
系数为1
y
x
=
y
自变量的取值要符合实际
精彩展示
你还记得圆锥的体积公式是什么吗?
其中的字母表示什么?
精彩展示
如图,圆锥的高度是4厘米,当圆锥的底面半径由小到大变化时,圆锥的体积也随之发生了变化.
(1)在这个变化过程中,
自变量、因变量各是什么?
圆锥的底面半径的长度
是自变量
圆锥的体积是因变量
精彩展示
如图,圆锥的高度是4厘米,当圆锥的底面半径由小到大变化时,圆锥的体积也随之发生了变化.
(2)如果圆锥底面半径为 r
(厘米),那么圆锥的体积v
(厘米3)与r的关系式为
______________
精彩展示
如图,圆锥的高度是4厘米,当圆锥的底面半径由小到大变化时,圆锥的体积也随之发生了变化.
(3)当底面半径由1厘米变
化到10厘米时,圆锥的体
积由 厘米3
变化到 厘米3 .
精彩展示
3、如图所示,梯形上底的长是a ,下底的长是15,
高是8,上底变化时,梯形的面积随之改变。
(1)梯形面积S与上底长a之间的关系式是什么?
a
8
15
(3)当a=0时,S等于什么?此时它表示的什么?
(2)当a每增加1时,S如何变化?
(1) S=4a+60
解:
(2) a每增加1时,S增加4.
(3)a=0时,S=60,
此时它表示的是三角形的面积.
例1:
汽车油箱有汽油50 L,如果不再加油,那么油箱中的油量y(单位:L)随行驶路程 x(单位:km)的增加而减少,平均油耗为0.1L/km.
(1)题目中有哪些变量和常量?并指出自变量和因变量。
(2)写出表示y与x的关系的式子;指出自变量x的取值范围;
(3)汽车行驶200 km时,油箱中还有多少汽油?
精点精讲
1.汽车以50千米/每时的速度行驶,用 t (时)表示行驶时间, s(千米)表示行驶的路程,则 s =______;
2.某柴油机每时耗油 6千克,该车在行驶 t小时内耗去了Q千克油, 则 Q =______;
3..设等腰三角形的周长为60,腰为x,底为y,用变量x表示y,则y=_________;若y=20,则x=_________,此时该三角形的形状为__________________.
50t
6t
适时检测 (基础篇)
20
20
等边三角形
燃烧时间x/分 10 20 30 40 50 …
剩余长度y/cm 19 18 17 16 15 …
4.一支原长为20cm的蜡烛,点燃后,其剩余
长度y(cm)与燃烧时间x(分)之间的关系如
下表:
则剩余长度y(cm)与燃烧时间x(分)的关系式为 ,估计这支蜡烛最多可燃烧 分.
200
200
适时检测 (提高篇)
1.5.将一个长为20cm,宽为10cm的长方形的四个角,
分别剪去大小相等的正方形,若被剪去正方形
的边长为 x cm , 阴影部分的面积为 y(cm2) ,
则 y 与 x 的关系式是 .
适时检测 (探究篇)
6.如 图,小华在假期帮爷爷设计一边靠墙(墙长9米),
其余三边用12米长的篱笆围成一个长方形花圃.
(1)如果设花圃靠墙一边的长为x(米),
花圃的面积为多少?
(2)当长x 从4米变到6米时,
面积y 的变化如何?
(3)当长x 从6米变到8米时,面积 y的变化如何?
(4)随着x的增加,y的变化趋势如何?y什么时候最大?
2、列表与列关系式表示变量之间的关系各有
什么特点?
小结作业
3、作业:必做题:P68页1,2.
选做题:P68页4.
1、到今天为止我们一共学了几种方法来表示
自变量与因变量之间的关系?
列表格与列关系式两种方法
通过列表格,可以较直观地表示因变量随自变量变化而变化的情况.
利用关系式,我们可以根据一个自变量的值求出相应的因变量的值 .
时间在分分秒秒的流逝,
我们在点点滴滴的进步
汽车行驶路程随行驶时间而变化
聪明的乌鸦认识到:
1、瓶口的大小不可改变,水的量也不可改变;
2、但瓶中水的高度是可以改变的,投的石块越多则水面就越高
情景引入
1kg
2kg
3kg
某弹簧的自然长度为3cm,在弹性限度内所挂的物体的重量x 每增加1 kg ,弹簧长度y增加0.5cm。
x/kg 1 2 3 4 5 ……
y/cm ……
上表数据,y与x之间的关系还可以怎样表示呢?
3.5
y = 3+0.5x
4
4.5
5
5.5
§3.2用关系式表示的
变量间关系
北师大版七年级数学下册
第三章 变量之间的关系
自主学习
同学们自主学习课本P66页内容
3、如图所示,梯形上底的长是a ,下底的长是15,
高是8,上底变化时,梯形的面积随之改变。
(1)梯形面积S与上底长a之间的关系式是什么?
(2)当a每增加1时,S如何变化?
(3)当a=0时,S等于什么?此时它表示的什么?
a
8
15
合作探究
(3)这个过程中哪个量是自变量,哪个量是
因变量?
(1)决定一个三角形的面积的因素有哪些?
(2)若△ABC底边BC上的高是6厘米,三角形的顶点C沿底边BC 所在直线向点C运动时,三角形的面积发生了怎样的变化?
A
C
B
C
C
C
精彩展示
(4)如果三角形的底边长为 x(厘米),那么三角形的面积y(厘米2)可以表示为 ________
y =3x
(5)当底边长从12厘米变化到3厘米时,
三角形的面积从_____厘米2变化
到_____厘米2.
36
9
精彩展示
y=3x表示了 和 之间 的关系,它是变量 随 变化的关系式.
三角形底边长 x
面积 y
3x
含自变量代数式
因变量
系数为1
y
x
=
y
自变量的取值要符合实际
精彩展示
你还记得圆锥的体积公式是什么吗?
其中的字母表示什么?
精彩展示
如图,圆锥的高度是4厘米,当圆锥的底面半径由小到大变化时,圆锥的体积也随之发生了变化.
(1)在这个变化过程中,
自变量、因变量各是什么?
圆锥的底面半径的长度
是自变量
圆锥的体积是因变量
精彩展示
如图,圆锥的高度是4厘米,当圆锥的底面半径由小到大变化时,圆锥的体积也随之发生了变化.
(2)如果圆锥底面半径为 r
(厘米),那么圆锥的体积v
(厘米3)与r的关系式为
______________
精彩展示
如图,圆锥的高度是4厘米,当圆锥的底面半径由小到大变化时,圆锥的体积也随之发生了变化.
(3)当底面半径由1厘米变
化到10厘米时,圆锥的体
积由 厘米3
变化到 厘米3 .
精彩展示
3、如图所示,梯形上底的长是a ,下底的长是15,
高是8,上底变化时,梯形的面积随之改变。
(1)梯形面积S与上底长a之间的关系式是什么?
a
8
15
(3)当a=0时,S等于什么?此时它表示的什么?
(2)当a每增加1时,S如何变化?
(1) S=4a+60
解:
(2) a每增加1时,S增加4.
(3)a=0时,S=60,
此时它表示的是三角形的面积.
例1:
汽车油箱有汽油50 L,如果不再加油,那么油箱中的油量y(单位:L)随行驶路程 x(单位:km)的增加而减少,平均油耗为0.1L/km.
(1)题目中有哪些变量和常量?并指出自变量和因变量。
(2)写出表示y与x的关系的式子;指出自变量x的取值范围;
(3)汽车行驶200 km时,油箱中还有多少汽油?
精点精讲
1.汽车以50千米/每时的速度行驶,用 t (时)表示行驶时间, s(千米)表示行驶的路程,则 s =______;
2.某柴油机每时耗油 6千克,该车在行驶 t小时内耗去了Q千克油, 则 Q =______;
3..设等腰三角形的周长为60,腰为x,底为y,用变量x表示y,则y=_________;若y=20,则x=_________,此时该三角形的形状为__________________.
50t
6t
适时检测 (基础篇)
20
20
等边三角形
燃烧时间x/分 10 20 30 40 50 …
剩余长度y/cm 19 18 17 16 15 …
4.一支原长为20cm的蜡烛,点燃后,其剩余
长度y(cm)与燃烧时间x(分)之间的关系如
下表:
则剩余长度y(cm)与燃烧时间x(分)的关系式为 ,估计这支蜡烛最多可燃烧 分.
200
200
适时检测 (提高篇)
1.5.将一个长为20cm,宽为10cm的长方形的四个角,
分别剪去大小相等的正方形,若被剪去正方形
的边长为 x cm , 阴影部分的面积为 y(cm2) ,
则 y 与 x 的关系式是 .
适时检测 (探究篇)
6.如 图,小华在假期帮爷爷设计一边靠墙(墙长9米),
其余三边用12米长的篱笆围成一个长方形花圃.
(1)如果设花圃靠墙一边的长为x(米),
花圃的面积为多少?
(2)当长x 从4米变到6米时,
面积y 的变化如何?
(3)当长x 从6米变到8米时,面积 y的变化如何?
(4)随着x的增加,y的变化趋势如何?y什么时候最大?
2、列表与列关系式表示变量之间的关系各有
什么特点?
小结作业
3、作业:必做题:P68页1,2.
选做题:P68页4.
1、到今天为止我们一共学了几种方法来表示
自变量与因变量之间的关系?
列表格与列关系式两种方法
通过列表格,可以较直观地表示因变量随自变量变化而变化的情况.
利用关系式,我们可以根据一个自变量的值求出相应的因变量的值 .
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
