华东师大版数学九年级上册 23.2 相似图形 课件(共22张ppt)
文档属性
| 名称 | 华东师大版数学九年级上册 23.2 相似图形 课件(共22张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 231.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-03 00:00:00 | ||
图片预览






文档简介
(共22张PPT)
相似图形
请欣赏
下列每组中的两幅图有何共同点
找一找:下列图形中哪些是相似图形?
像这样,形状相同的图形是相似图形。
1.你能举出生活中所见过的相似的图形吗?
想一想
2.同学们,还记得全等的图形吗?说一说全等的图形和相似的图形之间有什么联系与区别!
观察这幅图形,你有什么发现?
操作
看导学稿,量出图中两三角形的所有边的长度和所有角的度数。
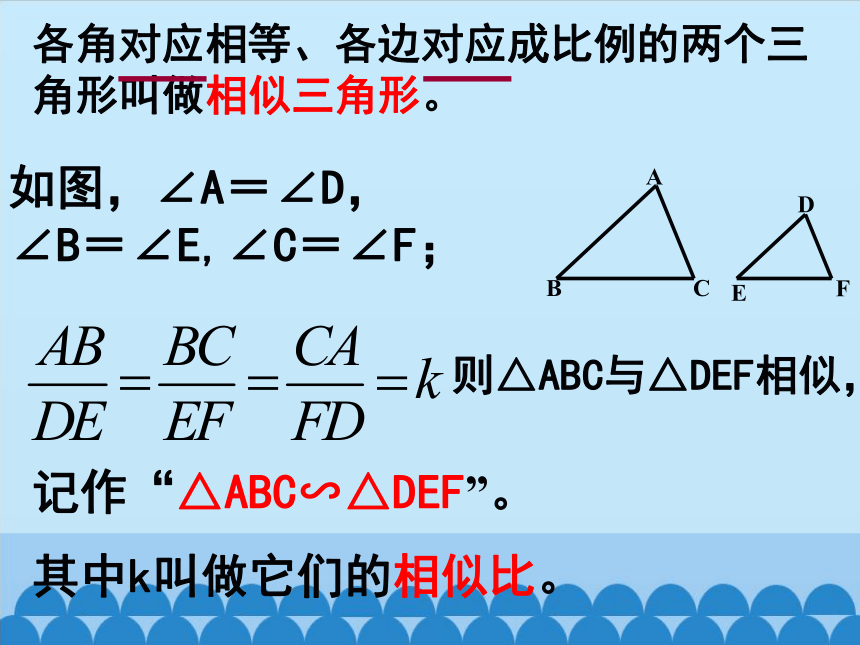
各角对应相等、各边对应成比例的两个三角形叫做相似三角形。
A
B
C
D
E
F
如图,∠A=∠D, ∠B=∠E,∠C=∠F;
则△ABC与△DEF相似,
记作“△ABC∽△DEF”。
其中k叫做它们的相似比。
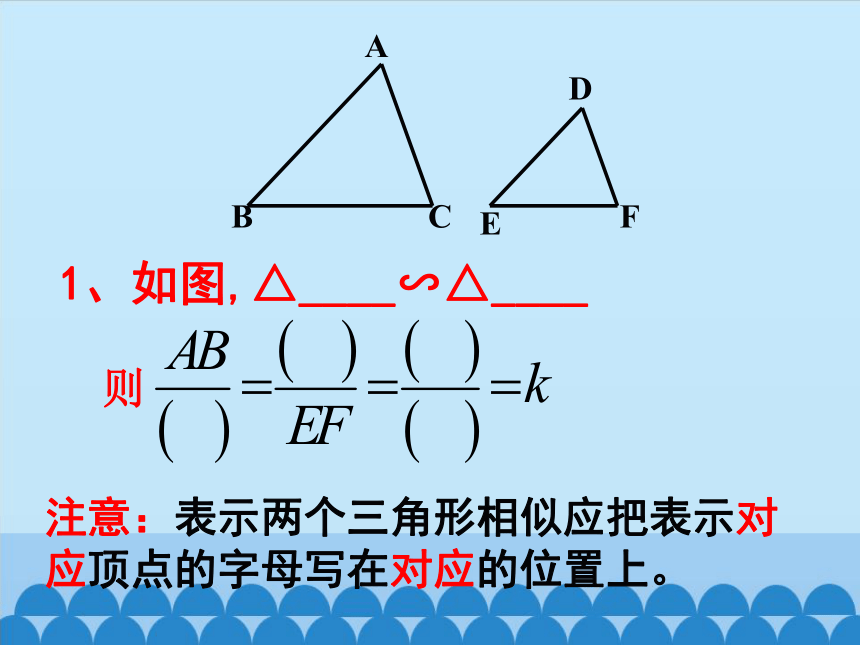
注意:表示两个三角形相似应把表示对应顶点的字母写在对应的位置上。
1、如图,△____∽△____
A
B
C
D
E
F
则
则△ABC与 的相似比是 ,
2、若△ABC∽ 且
与△ABC的相似比是 。
1:2
2:1
3、如果k=1,这两个三角形有怎样的关系?
分别根据下列已知条件,写出各组相似三角
形的对应边的比例式:
①如图,已知△ADE∽△ABC,
则 = =_____
试一试
A
B
C
D
E
②如图,已知△OAB∽△OCD,
则 = = _____
试一试
A
C
D
O
B
③如图,已知△ABC∽△ACD,
则 = = _____
试一试
A
B
C
D
试一试
在网格纸上任意画一个顶点在格点上的多边形,请你的同桌在同样的网格纸上画一个与它相似的图形
类似地,如果两个边数相同的多边形的对应角相等,对应边成比例,那么这两个多边形相似,相似多边形的对应边的比叫做相似比。
例1:
A
B
C
A′
B′
C′
75°
45°
45°
α
β
8
10
6
如图,△ABC∽△A′B′C′,求∠α、∠β的大小和A′C′的长.
如图,已知△ABC∽△ADE,AB=30cm,
BD=18cm,BC=20cm,∠BAC=75°,∠ABC=40°
求:(1)∠ADE和∠AED的度数;
(2)DE的长.
练习:
E
D
C
B
A
例2:
A
B
C
D
E
F
如图,D、E、F分别是△ABC三边的中点,△DEF与△ABC相似吗?为什么?
3
2
1
小 结
1.形状相同的图形是相似形.
2.相似三角形,相似多边形及相似比的 概念.
通过本节课,你学到了哪些知识?
1.下列说法正确的是( )
A.所有的等腰三角形都相似;
B.所有的菱形都相似;
C.所有的矩形都相似;
D.所有的正方形都相似.
D
课堂反馈:
2.在放大10倍的放大镜下所看到的图形( )
A.与原图形不相似;
B.与原图形相似,相似比为1:10;
C.与原图形相似,相似比为10:1;
D.与原图形相似,相似比为不确定.
C
谢谢!
相似图形
请欣赏
下列每组中的两幅图有何共同点
找一找:下列图形中哪些是相似图形?
像这样,形状相同的图形是相似图形。
1.你能举出生活中所见过的相似的图形吗?
想一想
2.同学们,还记得全等的图形吗?说一说全等的图形和相似的图形之间有什么联系与区别!
观察这幅图形,你有什么发现?
操作
看导学稿,量出图中两三角形的所有边的长度和所有角的度数。
各角对应相等、各边对应成比例的两个三角形叫做相似三角形。
A
B
C
D
E
F
如图,∠A=∠D, ∠B=∠E,∠C=∠F;
则△ABC与△DEF相似,
记作“△ABC∽△DEF”。
其中k叫做它们的相似比。
注意:表示两个三角形相似应把表示对应顶点的字母写在对应的位置上。
1、如图,△____∽△____
A
B
C
D
E
F
则
则△ABC与 的相似比是 ,
2、若△ABC∽ 且
与△ABC的相似比是 。
1:2
2:1
3、如果k=1,这两个三角形有怎样的关系?
分别根据下列已知条件,写出各组相似三角
形的对应边的比例式:
①如图,已知△ADE∽△ABC,
则 = =_____
试一试
A
B
C
D
E
②如图,已知△OAB∽△OCD,
则 = = _____
试一试
A
C
D
O
B
③如图,已知△ABC∽△ACD,
则 = = _____
试一试
A
B
C
D
试一试
在网格纸上任意画一个顶点在格点上的多边形,请你的同桌在同样的网格纸上画一个与它相似的图形
类似地,如果两个边数相同的多边形的对应角相等,对应边成比例,那么这两个多边形相似,相似多边形的对应边的比叫做相似比。
例1:
A
B
C
A′
B′
C′
75°
45°
45°
α
β
8
10
6
如图,△ABC∽△A′B′C′,求∠α、∠β的大小和A′C′的长.
如图,已知△ABC∽△ADE,AB=30cm,
BD=18cm,BC=20cm,∠BAC=75°,∠ABC=40°
求:(1)∠ADE和∠AED的度数;
(2)DE的长.
练习:
E
D
C
B
A
例2:
A
B
C
D
E
F
如图,D、E、F分别是△ABC三边的中点,△DEF与△ABC相似吗?为什么?
3
2
1
小 结
1.形状相同的图形是相似形.
2.相似三角形,相似多边形及相似比的 概念.
通过本节课,你学到了哪些知识?
1.下列说法正确的是( )
A.所有的等腰三角形都相似;
B.所有的菱形都相似;
C.所有的矩形都相似;
D.所有的正方形都相似.
D
课堂反馈:
2.在放大10倍的放大镜下所看到的图形( )
A.与原图形不相似;
B.与原图形相似,相似比为1:10;
C.与原图形相似,相似比为10:1;
D.与原图形相似,相似比为不确定.
C
谢谢!
