沪科版数学九年级上册 第22章 相似形 课件(共19张PPT)
文档属性
| 名称 | 沪科版数学九年级上册 第22章 相似形 课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 248.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-03 17:23:32 | ||
图片预览





文档简介
(共19张PPT)
第22章 相似形(通用)
相似三角形
相似三角形的性质
相似三角形的基本类型
比例线段
比例的性质
平行线分线段成比例
相似三角形的判定
=
=
点C把线段AB分成两条线段AC和BC,且 那么就说线段AB被点C黄金分割,点C叫做线段AB的黄金分割点,AC与AB的比叫做黄金比,即
性质1:
性质2:
性质3:
黄金
分割:
①
②
平行线分线段成比例
两条直线被一组平行线所截,所得的对应线段成比例
平行于三角形一边的直线截其他两边(两边的延长线),所得的对应线段成比例
定理:
推论:
相似三角形的性质
1. 相似三角形对应角③ ,对应边成比例
2. 相似三角形对应线段(边、高、④ 、角平分线)成比例,且等于相似比
3.相似三角形的周长比等于相似比,面积比等于⑤
相等
中线
相似比的平方
相似三角形的判定
一般三角形
直角三角形
2.两角对应相等,两三角形相似
3.两边对应成比例,且⑥ 相等,两三角形相似;
4.三边对应成比例,两三角形相似
1.一组锐角对应相等
2.两条边对应成比例
夹角
①两直角边对应成比例
②斜边和一直角边对应成比例
1.平行三角形一边的直线和其他两边相交(或两边的延长线),所构成的三角形与原三角形相似.
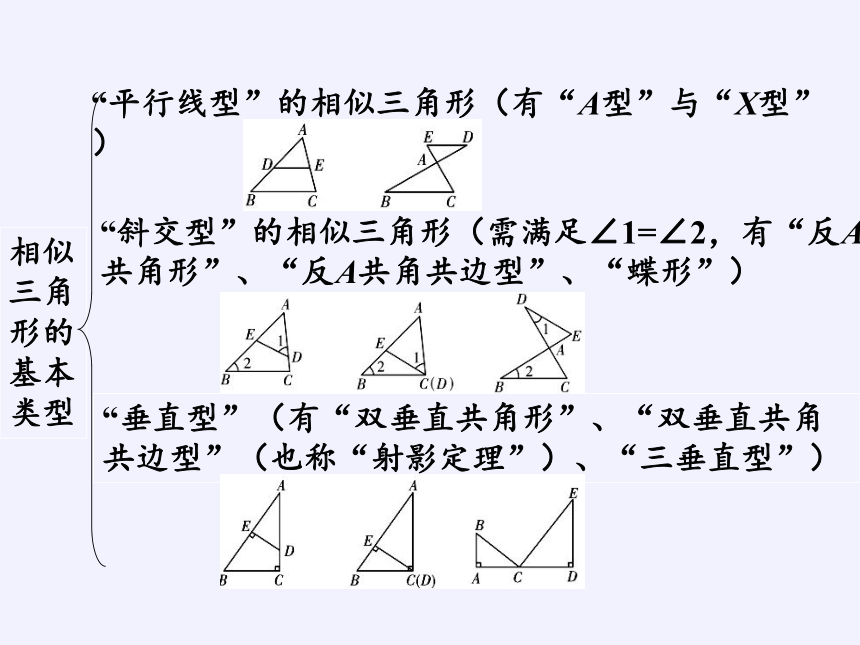
相似三角形的基本类型
“垂直型”(有“双垂直共角形”、“双垂直共角共边型”(也称“射影定理”)、“三垂直型”)
“平行线型”的相似三角形(有“A型”与“X型”)
“斜交型”的相似三角形(需满足∠1=∠2,有“反A共角形”、“反A共角共边型”、“蝶形”)
例:在四边形ABCD中, ∠A= ∠B= ∠3 ,点E为AB边中点,求证:CE平分∠BCD
又∵点E为AB边中点
∴
∴CE平分∠BCD
∴∠DCE = ∠BCE
∴△ DCE~ △ECB
又∵∠3= ∠B
∴△ DEA~ △ECB
∴
证明:∵ ∠1+ ∠2=180- ∠ A
∠2+ ∠4=180- ∠3
∠3= ∠A
∴ ∠1= ∠4
又∵∠A=∠B
例2 (2016合肥市第四次十校联考)如图,四边形ABCD 中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.
(1)求证:AC2=AB AD;
(2)求证:CE∥AD;
(3)若AD=5,AB=7,求 的值.
(1)【思维教练】要证AC 2=AB AD,则可通过求证△ADC∽△ACB,然后用相似三角形的对应边成比例得证;
证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴AD∶AC=AC∶AB,
∴AC2=AB AD;
(2)【思维教练】要证CE∥AD,要结合已知条件及直角三角形斜边上的中线等于斜边的一半这一性质可得∠DAC=∠ECA,利用平行线的判定定理即可得证;
证明:∵E为AB的中点,
∴CE= AB=AE,
∴∠EAC=∠ECA,
∵∠DAC=∠CAB,
∴∠DAC=∠ECA,
∴CE∥AD;
(3)【思维教练】要求 的值,由题意无法直接得到,由CE∥AD可得△AFD ∽△CFE,根据相似三角形的对应边成比例来求得 值,进而得到 的值.
解:∵CE∥AD,
∴△AFD∽△CFE,∴AD∶CE=AF∶CF,
∵CE= AB,∴CE= ×7= .
∵AD=5,
∴ ,∴ .
例3 (2016武汉)在△ABC中,P为边AB上一点.
(1)如图①,若∠ACP=∠B,求证:AC2=AP AB;
(2)若M为CP的中点,AC=2.
①如图②,若∠PBM=∠ACP,AB=3,求BP的长;
②如图③,若∠ABC=45°,∠A=∠BMP=60°,直接写出BP的长.
(2)①解:如解图①,延长BM至E点使得ME=BM,并且BE交AC于点N,连接CE,
∵MP=MC,∠BMP=∠EMC,MB=ME,
∴△BPM≌△ECM(SAS),
∴∠ABN=∠E,BP=CE,
∵△APC∽△ANB,
∴ ,
(1)证明:∵∠A=∠A,∠ACP=∠B,
∴△ACP∽△ABC,
∴ ,∴AC2=AP AB.
设PB=x,则AP=3-x,
∴AN= (3-x)= - x,
则CN=2- (3-x)= x- ,
∵∠ABN=∠E,∠ANB=∠CNE,
∴△NCE∽△NAB,
∴ ,即 ,
解得,x= (或x=- ,舍去).
∵BP=CE,∴BP= .
②解:BP= -1.
【解法提示】设BP=x,如解图②,过点C作CH⊥AB于点H,延长AB至E,使BE=BP,则AH=AC cos∠A=1,BH=CH=AC sin∠A= ,HE=x+ ,
∴EC2=EH 2+HC 2=(x+ )2+( )2=
x2+2 x+6,
∵M是PC的中点,
∴BM是△PEC的中位线,
∴BM∥EC,
∴∠PCE=∠PMB=∠A,
∵∠E=∠E,
∴△ECP∽△EAC,
∴EC2=EP EA,
即x2+2 x+6=2x(x+ +1),
解得x= -1(或x=- -1,舍去).
∴BP的长为 -1.
课堂小结
通过本节课的学习,你的收获有哪些?
疑问有哪些?请与你的同学相互交流一下。
谢 谢
第22章 相似形(通用)
相似三角形
相似三角形的性质
相似三角形的基本类型
比例线段
比例的性质
平行线分线段成比例
相似三角形的判定
=
=
点C把线段AB分成两条线段AC和BC,且 那么就说线段AB被点C黄金分割,点C叫做线段AB的黄金分割点,AC与AB的比叫做黄金比,即
性质1:
性质2:
性质3:
黄金
分割:
①
②
平行线分线段成比例
两条直线被一组平行线所截,所得的对应线段成比例
平行于三角形一边的直线截其他两边(两边的延长线),所得的对应线段成比例
定理:
推论:
相似三角形的性质
1. 相似三角形对应角③ ,对应边成比例
2. 相似三角形对应线段(边、高、④ 、角平分线)成比例,且等于相似比
3.相似三角形的周长比等于相似比,面积比等于⑤
相等
中线
相似比的平方
相似三角形的判定
一般三角形
直角三角形
2.两角对应相等,两三角形相似
3.两边对应成比例,且⑥ 相等,两三角形相似;
4.三边对应成比例,两三角形相似
1.一组锐角对应相等
2.两条边对应成比例
夹角
①两直角边对应成比例
②斜边和一直角边对应成比例
1.平行三角形一边的直线和其他两边相交(或两边的延长线),所构成的三角形与原三角形相似.
相似三角形的基本类型
“垂直型”(有“双垂直共角形”、“双垂直共角共边型”(也称“射影定理”)、“三垂直型”)
“平行线型”的相似三角形(有“A型”与“X型”)
“斜交型”的相似三角形(需满足∠1=∠2,有“反A共角形”、“反A共角共边型”、“蝶形”)
例:在四边形ABCD中, ∠A= ∠B= ∠3 ,点E为AB边中点,求证:CE平分∠BCD
又∵点E为AB边中点
∴
∴CE平分∠BCD
∴∠DCE = ∠BCE
∴△ DCE~ △ECB
又∵∠3= ∠B
∴△ DEA~ △ECB
∴
证明:∵ ∠1+ ∠2=180- ∠ A
∠2+ ∠4=180- ∠3
∠3= ∠A
∴ ∠1= ∠4
又∵∠A=∠B
例2 (2016合肥市第四次十校联考)如图,四边形ABCD 中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点.
(1)求证:AC2=AB AD;
(2)求证:CE∥AD;
(3)若AD=5,AB=7,求 的值.
(1)【思维教练】要证AC 2=AB AD,则可通过求证△ADC∽△ACB,然后用相似三角形的对应边成比例得证;
证明:∵AC平分∠DAB,
∴∠DAC=∠CAB,
∵∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴AD∶AC=AC∶AB,
∴AC2=AB AD;
(2)【思维教练】要证CE∥AD,要结合已知条件及直角三角形斜边上的中线等于斜边的一半这一性质可得∠DAC=∠ECA,利用平行线的判定定理即可得证;
证明:∵E为AB的中点,
∴CE= AB=AE,
∴∠EAC=∠ECA,
∵∠DAC=∠CAB,
∴∠DAC=∠ECA,
∴CE∥AD;
(3)【思维教练】要求 的值,由题意无法直接得到,由CE∥AD可得△AFD ∽△CFE,根据相似三角形的对应边成比例来求得 值,进而得到 的值.
解:∵CE∥AD,
∴△AFD∽△CFE,∴AD∶CE=AF∶CF,
∵CE= AB,∴CE= ×7= .
∵AD=5,
∴ ,∴ .
例3 (2016武汉)在△ABC中,P为边AB上一点.
(1)如图①,若∠ACP=∠B,求证:AC2=AP AB;
(2)若M为CP的中点,AC=2.
①如图②,若∠PBM=∠ACP,AB=3,求BP的长;
②如图③,若∠ABC=45°,∠A=∠BMP=60°,直接写出BP的长.
(2)①解:如解图①,延长BM至E点使得ME=BM,并且BE交AC于点N,连接CE,
∵MP=MC,∠BMP=∠EMC,MB=ME,
∴△BPM≌△ECM(SAS),
∴∠ABN=∠E,BP=CE,
∵△APC∽△ANB,
∴ ,
(1)证明:∵∠A=∠A,∠ACP=∠B,
∴△ACP∽△ABC,
∴ ,∴AC2=AP AB.
设PB=x,则AP=3-x,
∴AN= (3-x)= - x,
则CN=2- (3-x)= x- ,
∵∠ABN=∠E,∠ANB=∠CNE,
∴△NCE∽△NAB,
∴ ,即 ,
解得,x= (或x=- ,舍去).
∵BP=CE,∴BP= .
②解:BP= -1.
【解法提示】设BP=x,如解图②,过点C作CH⊥AB于点H,延长AB至E,使BE=BP,则AH=AC cos∠A=1,BH=CH=AC sin∠A= ,HE=x+ ,
∴EC2=EH 2+HC 2=(x+ )2+( )2=
x2+2 x+6,
∵M是PC的中点,
∴BM是△PEC的中位线,
∴BM∥EC,
∴∠PCE=∠PMB=∠A,
∵∠E=∠E,
∴△ECP∽△EAC,
∴EC2=EP EA,
即x2+2 x+6=2x(x+ +1),
解得x= -1(或x=- -1,舍去).
∴BP的长为 -1.
课堂小结
通过本节课的学习,你的收获有哪些?
疑问有哪些?请与你的同学相互交流一下。
谢 谢
