沪科版数学九年级上册第23章 解直角三角形 复习教案
文档属性
| 名称 | 沪科版数学九年级上册第23章 解直角三角形 复习教案 |

|
|
| 格式 | docx | ||
| 文件大小 | 58.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-03 00:00:00 | ||
图片预览

文档简介
第23章 解直角三角形复习
一.教学内容
第23章 解直角三角形复习
二. 重点、难点:
1. 重点:
(1)探索直角三角形中锐角三角函数值与三边之间的关系.掌握三角函数定义式:sinA=,cosA=,tanA=,
(2)掌握30°、45°、60°等特殊角的三角函数值,并会进行有关特殊角的三角函数值的计算.
(3)会使用计算器由已知锐角求它的三角函数值,由已知三角函数值求它对应的锐角.
2. 难点:
(1)能够运用三角函数解决与直角形有关的简单的实际问题.
(2)能综合运用直角三角形的勾股定理与边角关系解决简单的实际问题,提高数学建模能力.
三. 知识梳理:
1. 锐角三角函数
(1)锐角三角函数的定义
我们规定:
sinA=,cosA=,tanA=,
锐角的正弦、余弦、正切统称为锐角的三角函数.
用计算器由已知角求三角函数值或由已知三角函数值求角度
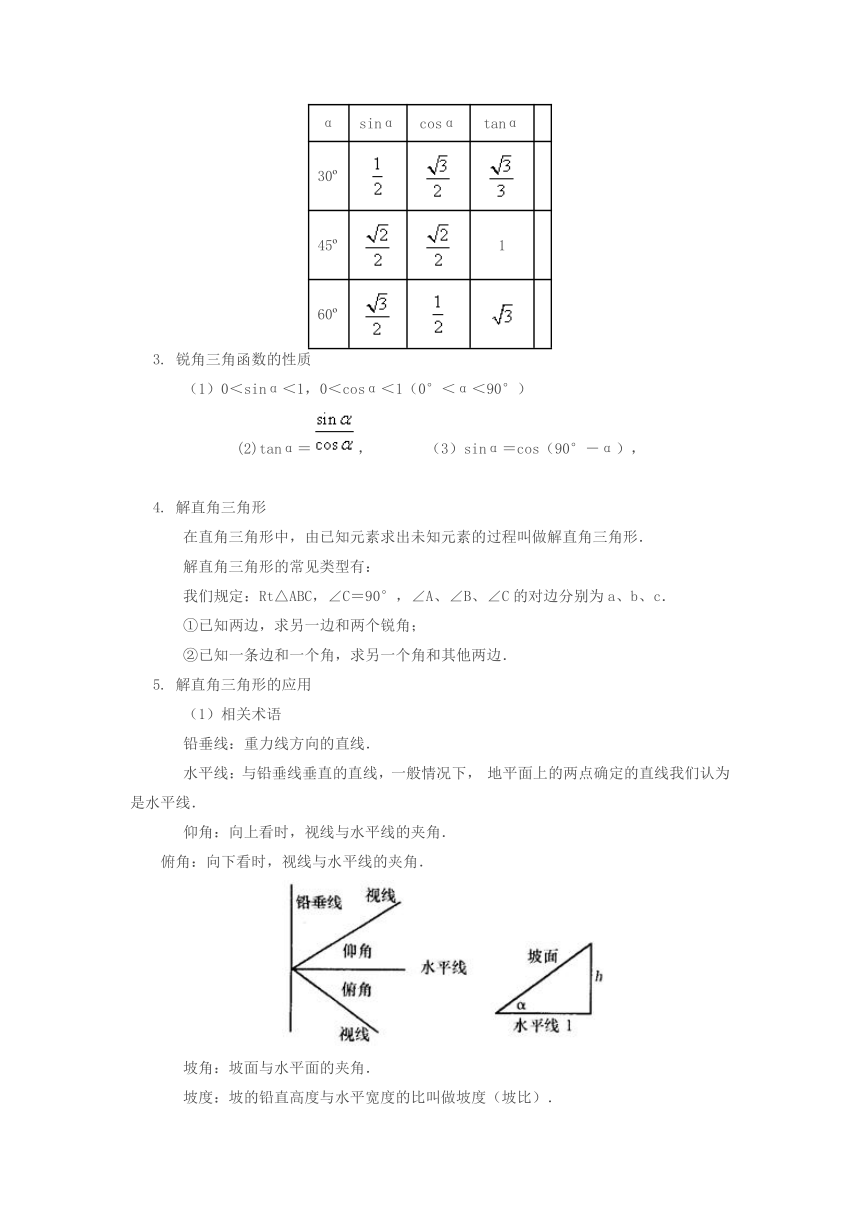
2. 特殊角的三角函数值
α sinα cosα tanα
30
45 1
60
3. 锐角三角函数的性质
(1)0<sinα<1,0<cosα<1(0°<α<90°)
(2)tanα=, (3)sinα=cos(90°-α),
4. 解直角三角形
在直角三角形中,由已知元素求出未知元素的过程叫做解直角三角形.
解直角三角形的常见类型有:
我们规定:Rt△ABC,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c.
①已知两边,求另一边和两个锐角;
②已知一条边和一个角,求另一个角和其他两边.
5. 解直角三角形的应用
(1)相关术语
铅垂线:重力线方向的直线.
水平线:与铅垂线垂直的直线,一般情况下,地平面上的两点确定的直线我们认为是水平线.
仰角:向上看时,视线与水平线的夹角.
俯角:向下看时,视线与水平线的夹角.
坡角:坡面与水平面的夹角.
坡度:坡的铅直高度与水平宽度的比叫做坡度(坡比).
一般情况下,我们用h表示坡的铅直高度,用l表示水平宽度,用i表示坡度,即:i==tanα.
方向角:指北或指南方向线与目标方向线所成的小于90°的水平角叫做方向角.
如图:
(2)应用解直角三角形来解决实际问题时,要注意:
①计算结果的精确度要求,一般说来中间量要多取一位有效数字.
②在题目中求未知时,应尽量选用直接由已知求未知.
③遇到非直角三角形时,常常要作辅助线才能应用解直角三角形知识来解答.
四,应用举例【典型例题】
例1. 计算.
(1)sin45°-cos60°;
(2)cos245°+tan60°cos30°;
(3);
(4).
分析:略
例2. 如图,一艘轮船从离A观察站的正北20海里处的B港处向正西航行,观察站第一次测得该船在A地北偏西30°的C处,一个半小时后,又测得该船在A地的北偏西的D处,求此船的速度.
分析:根据速度等于路程除以时间,必须求到DC的长,观察图形,DC=DB-CB,而BD在Rt△ABD中可求,BC在Rt△ABC中可求.
解:在Rt△ABC中,BC=AB×tan30°=20×=20(海里).
在Rt△ABD中,BD=AB×tan60°=20×=60(海里).
所以DC=DB-CB=60-20=40(海里).
船的速度是:40÷1.5=26(海里).
答:船的速度是26海里.
例3. 如图所示,河对岸有一座铁塔AB,若在河这边C、D处分别用测角仪器测得塔顶A的仰角为30°,45°,已知CD=30米,求铁塔的高.(结果保留根号)
分析:设塔高为x米,根据条件∠ADB=45°,可得BD=AB=x米,在直角三角形ABC中,根据∠C=30°,即tanC=可求.
解:设AB=x,在Rt△ABD中,∠ADB=45°,∴AB=BD=x.
在Rt△ABC中,∠C=30°,且BC=CD+BD=30+x,tanC=
所以tan30°=,即=,x=(15+15)(米).
答:塔高AB为15+15米.
五、学习体会
通过本节课的学习,你有哪些收获,还有哪些困惑?
六,课外独立练习
1、已知tan=,是锐角,则sin= ,cos= .
2、若tan(α+10°)=,则锐角α的度数是 .
3、如图,已知正方形ABCD的边长为2,如果将线段BD绕着点B旋转后,点D落在CB的延长线上的D′处,那么tan∠BAD′等于 .
.
4, 已知tanα=,求的值.
5, 如图,如果△ABC中∠C是锐角,BC=,AC=.证明:
(提示:过A作AD⊥BC于D,则△ADC是直角三角形)
七,教学反思:
一.教学内容
第23章 解直角三角形复习
二. 重点、难点:
1. 重点:
(1)探索直角三角形中锐角三角函数值与三边之间的关系.掌握三角函数定义式:sinA=,cosA=,tanA=,
(2)掌握30°、45°、60°等特殊角的三角函数值,并会进行有关特殊角的三角函数值的计算.
(3)会使用计算器由已知锐角求它的三角函数值,由已知三角函数值求它对应的锐角.
2. 难点:
(1)能够运用三角函数解决与直角形有关的简单的实际问题.
(2)能综合运用直角三角形的勾股定理与边角关系解决简单的实际问题,提高数学建模能力.
三. 知识梳理:
1. 锐角三角函数
(1)锐角三角函数的定义
我们规定:
sinA=,cosA=,tanA=,
锐角的正弦、余弦、正切统称为锐角的三角函数.
用计算器由已知角求三角函数值或由已知三角函数值求角度
2. 特殊角的三角函数值
α sinα cosα tanα
30
45 1
60
3. 锐角三角函数的性质
(1)0<sinα<1,0<cosα<1(0°<α<90°)
(2)tanα=, (3)sinα=cos(90°-α),
4. 解直角三角形
在直角三角形中,由已知元素求出未知元素的过程叫做解直角三角形.
解直角三角形的常见类型有:
我们规定:Rt△ABC,∠C=90°,∠A、∠B、∠C的对边分别为a、b、c.
①已知两边,求另一边和两个锐角;
②已知一条边和一个角,求另一个角和其他两边.
5. 解直角三角形的应用
(1)相关术语
铅垂线:重力线方向的直线.
水平线:与铅垂线垂直的直线,一般情况下,地平面上的两点确定的直线我们认为是水平线.
仰角:向上看时,视线与水平线的夹角.
俯角:向下看时,视线与水平线的夹角.
坡角:坡面与水平面的夹角.
坡度:坡的铅直高度与水平宽度的比叫做坡度(坡比).
一般情况下,我们用h表示坡的铅直高度,用l表示水平宽度,用i表示坡度,即:i==tanα.
方向角:指北或指南方向线与目标方向线所成的小于90°的水平角叫做方向角.
如图:
(2)应用解直角三角形来解决实际问题时,要注意:
①计算结果的精确度要求,一般说来中间量要多取一位有效数字.
②在题目中求未知时,应尽量选用直接由已知求未知.
③遇到非直角三角形时,常常要作辅助线才能应用解直角三角形知识来解答.
四,应用举例【典型例题】
例1. 计算.
(1)sin45°-cos60°;
(2)cos245°+tan60°cos30°;
(3);
(4).
分析:略
例2. 如图,一艘轮船从离A观察站的正北20海里处的B港处向正西航行,观察站第一次测得该船在A地北偏西30°的C处,一个半小时后,又测得该船在A地的北偏西的D处,求此船的速度.
分析:根据速度等于路程除以时间,必须求到DC的长,观察图形,DC=DB-CB,而BD在Rt△ABD中可求,BC在Rt△ABC中可求.
解:在Rt△ABC中,BC=AB×tan30°=20×=20(海里).
在Rt△ABD中,BD=AB×tan60°=20×=60(海里).
所以DC=DB-CB=60-20=40(海里).
船的速度是:40÷1.5=26(海里).
答:船的速度是26海里.
例3. 如图所示,河对岸有一座铁塔AB,若在河这边C、D处分别用测角仪器测得塔顶A的仰角为30°,45°,已知CD=30米,求铁塔的高.(结果保留根号)
分析:设塔高为x米,根据条件∠ADB=45°,可得BD=AB=x米,在直角三角形ABC中,根据∠C=30°,即tanC=可求.
解:设AB=x,在Rt△ABD中,∠ADB=45°,∴AB=BD=x.
在Rt△ABC中,∠C=30°,且BC=CD+BD=30+x,tanC=
所以tan30°=,即=,x=(15+15)(米).
答:塔高AB为15+15米.
五、学习体会
通过本节课的学习,你有哪些收获,还有哪些困惑?
六,课外独立练习
1、已知tan=,是锐角,则sin= ,cos= .
2、若tan(α+10°)=,则锐角α的度数是 .
3、如图,已知正方形ABCD的边长为2,如果将线段BD绕着点B旋转后,点D落在CB的延长线上的D′处,那么tan∠BAD′等于 .
.
4, 已知tanα=,求的值.
5, 如图,如果△ABC中∠C是锐角,BC=,AC=.证明:
(提示:过A作AD⊥BC于D,则△ADC是直角三角形)
七,教学反思:
