沪科版数学九年级上册 22.3 相似三角形的性质 课件(共14张PPT)
文档属性
| 名称 | 沪科版数学九年级上册 22.3 相似三角形的性质 课件(共14张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 6.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-03 17:21:15 | ||
图片预览

文档简介
(共14张PPT)
22.3 相似三角形的性质
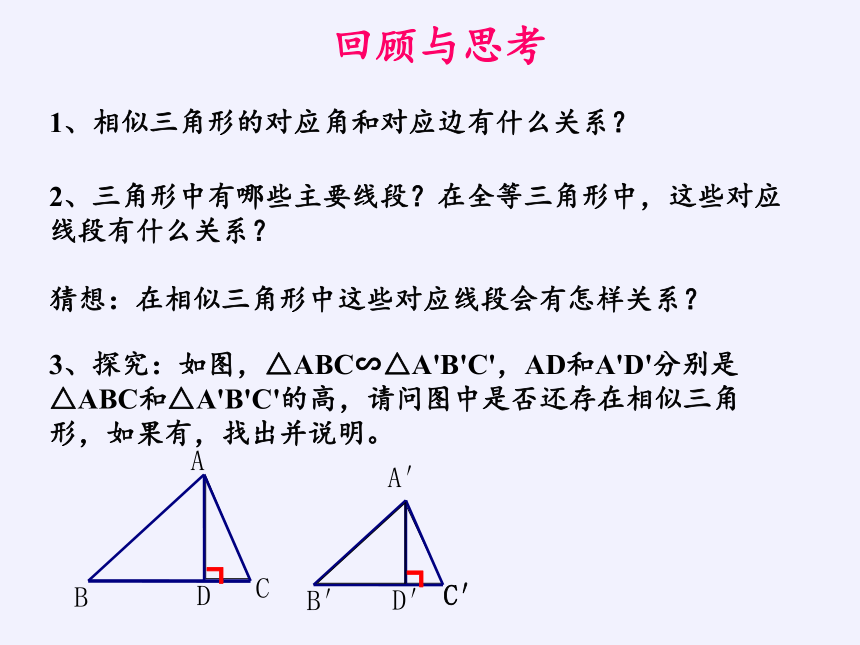
3、探究:如图,△ABC∽△A'B'C',AD和A'D'分别是△ABC和△A'B'C'的高,请问图中是否还存在相似三角形,如果有,找出并说明。
D′
C′
B′
┓
D
A
B
C
A′
┓
回顾与思考
1、相似三角形的对应角和对应边有什么关系?
2、三角形中有哪些主要线段?在全等三角形中,这些对应线段有什么关系?
猜想:在相似三角形中这些对应线段会有怎样关系?
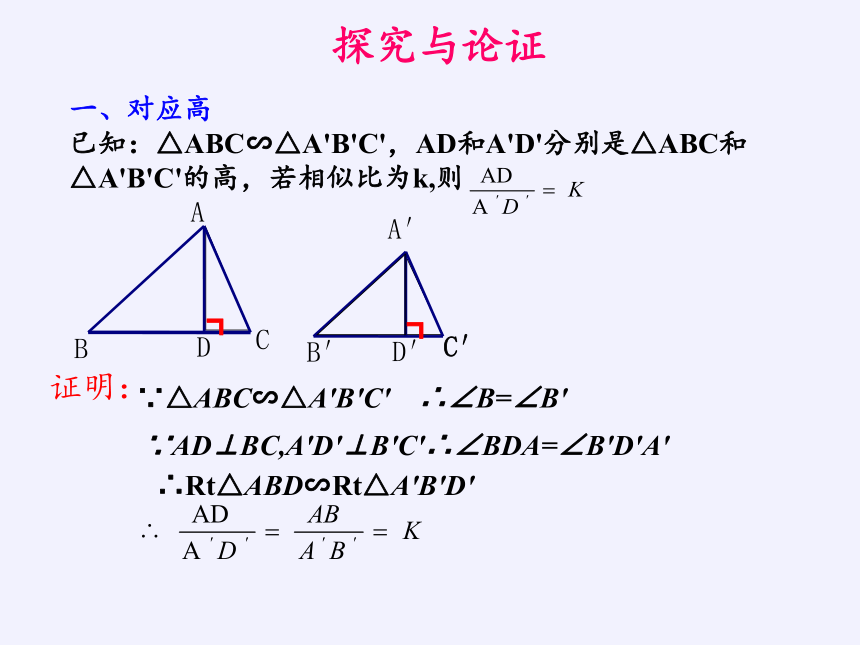
一、对应高
已知:△ABC∽△A'B'C',AD和A'D'分别是△ABC和△A'B'C'的高,若相似比为k,则
证明:
∵△ABC∽△A′B′C′
∴∠B=∠B′
∵AD⊥BC,A′D′⊥B′C′∴∠BDA=∠B′D′A′
∴Rt△ABD∽Rt△A′B′D′
探究与论证
D′
C′
B′
┓
D
A
B
C
A′
┓
D′
C′
D
A
B
C
A′
B′
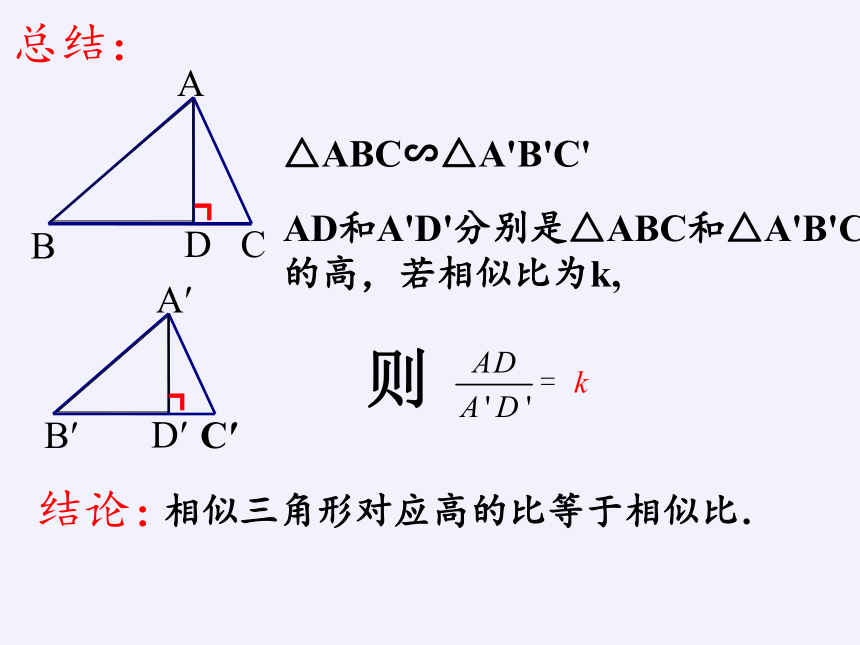
△ABC∽△A'B'C'
AD和A'D'分别是△ABC和△A'B'C'
的高,若相似比为k,
┓
┓
相似三角形对应高的比等于相似比.
结论:
总结:
则
证明:
∵△ABC∽△A′B′C′
∴∠B=∠B′;∠BAC=∠B′A′C′
∵∠BAD= ∠BAC, ∠B′A′D′= ∠B′A′C′
∴△ABD∽△A′B′D′
D
A
B
C
D'
A'
B'
C'
∴∠BAD=∠B′A′D′
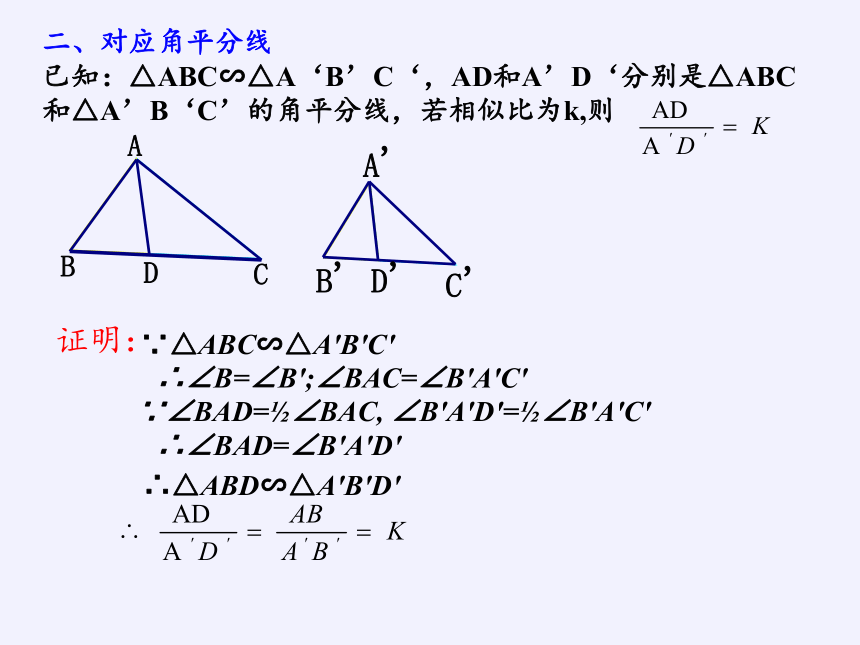
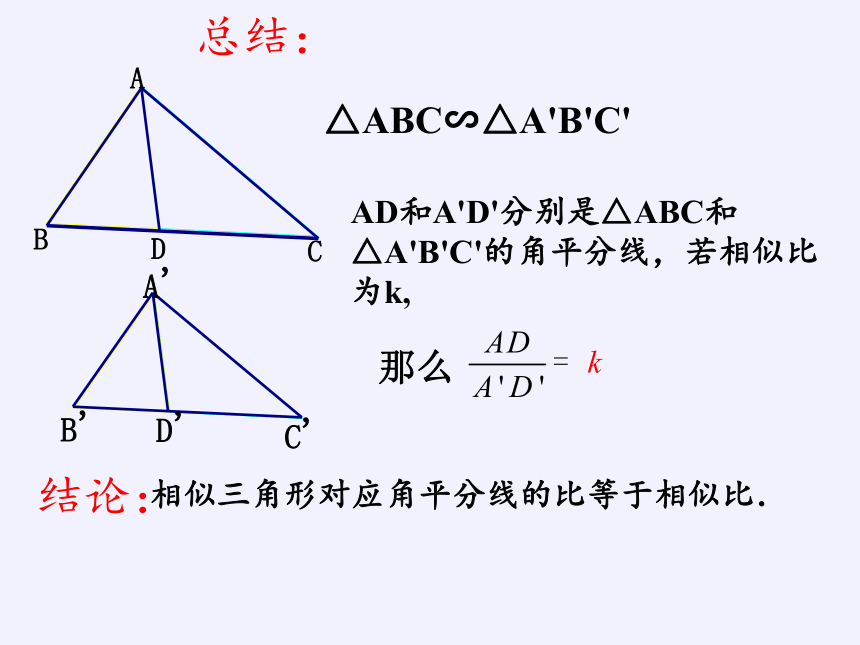
二、对应角平分线
已知:△ABC∽△A‘B’C‘,AD和A’D‘分别是△ABC和△A’B‘C’的角平分线,若相似比为k,则
D'
A'
B'
C'
D
A
B
C
相似三角形对应角平分线的比等于相似比.
结论:
△ABC∽△A'B'C'
AD和A'D'分别是△ABC和△A'B'C'的角平分线,若相似比为k,
那么
总结:
D′
C′
B′
D
A
B
C
A′
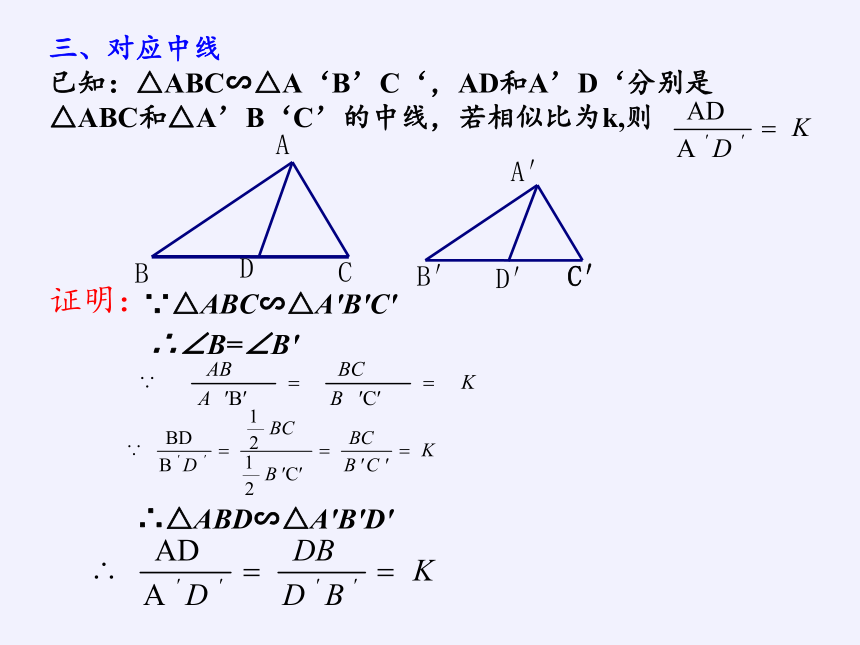
证明:
∵△ABC∽△A′B′C′
∴∠B=∠B′
∴△ABD∽△A′B′D′
三、对应中线
已知:△ABC∽△A‘B’C‘,AD和A’D‘分别是△ABC和△A’B‘C’的中线,若相似比为k,则
△ABC∽△A'B'C'
AD和A'D'分别是△ABC和△A'B'C'
的中线,若相似比为k,
那么
D
A
B
C
D'
A'
B'
C'
相似三角形对应中线的比等于相似比.
结论:
总结:
实践与应用
例1:课本90页 练习1
例2:电灯位于直径为1.8米的圆桌正上方3米处,圆桌与店面保持平行,并且在灯光下有直径为2.4米的圆形影子。请求灯泡距离地面的高度。
A
B
C
D
E
┐
┐
M
N
相似三角形的性质
(特别注意“对应”二字)
的比都等于相似比
小结与提高
对应角相等
对应边成比例
对应中线
对应高
对应角平分线
全等三角形与相似三角形性质比较
全等三角形 相似三角形
对应角相等 对应角相等
对应边相等 对应边的比等于相似比
对应高相等 对应高的比等于相似比
对应中线相等 对应中线的比等于相似比
对应角平分线相等 对应角平分线的比等于相似比
作业与拓展
1、教材P90-91:习题2、3、10
2、自学:教材P88:例1
谢 谢
22.3 相似三角形的性质
3、探究:如图,△ABC∽△A'B'C',AD和A'D'分别是△ABC和△A'B'C'的高,请问图中是否还存在相似三角形,如果有,找出并说明。
D′
C′
B′
┓
D
A
B
C
A′
┓
回顾与思考
1、相似三角形的对应角和对应边有什么关系?
2、三角形中有哪些主要线段?在全等三角形中,这些对应线段有什么关系?
猜想:在相似三角形中这些对应线段会有怎样关系?
一、对应高
已知:△ABC∽△A'B'C',AD和A'D'分别是△ABC和△A'B'C'的高,若相似比为k,则
证明:
∵△ABC∽△A′B′C′
∴∠B=∠B′
∵AD⊥BC,A′D′⊥B′C′∴∠BDA=∠B′D′A′
∴Rt△ABD∽Rt△A′B′D′
探究与论证
D′
C′
B′
┓
D
A
B
C
A′
┓
D′
C′
D
A
B
C
A′
B′
△ABC∽△A'B'C'
AD和A'D'分别是△ABC和△A'B'C'
的高,若相似比为k,
┓
┓
相似三角形对应高的比等于相似比.
结论:
总结:
则
证明:
∵△ABC∽△A′B′C′
∴∠B=∠B′;∠BAC=∠B′A′C′
∵∠BAD= ∠BAC, ∠B′A′D′= ∠B′A′C′
∴△ABD∽△A′B′D′
D
A
B
C
D'
A'
B'
C'
∴∠BAD=∠B′A′D′
二、对应角平分线
已知:△ABC∽△A‘B’C‘,AD和A’D‘分别是△ABC和△A’B‘C’的角平分线,若相似比为k,则
D'
A'
B'
C'
D
A
B
C
相似三角形对应角平分线的比等于相似比.
结论:
△ABC∽△A'B'C'
AD和A'D'分别是△ABC和△A'B'C'的角平分线,若相似比为k,
那么
总结:
D′
C′
B′
D
A
B
C
A′
证明:
∵△ABC∽△A′B′C′
∴∠B=∠B′
∴△ABD∽△A′B′D′
三、对应中线
已知:△ABC∽△A‘B’C‘,AD和A’D‘分别是△ABC和△A’B‘C’的中线,若相似比为k,则
△ABC∽△A'B'C'
AD和A'D'分别是△ABC和△A'B'C'
的中线,若相似比为k,
那么
D
A
B
C
D'
A'
B'
C'
相似三角形对应中线的比等于相似比.
结论:
总结:
实践与应用
例1:课本90页 练习1
例2:电灯位于直径为1.8米的圆桌正上方3米处,圆桌与店面保持平行,并且在灯光下有直径为2.4米的圆形影子。请求灯泡距离地面的高度。
A
B
C
D
E
┐
┐
M
N
相似三角形的性质
(特别注意“对应”二字)
的比都等于相似比
小结与提高
对应角相等
对应边成比例
对应中线
对应高
对应角平分线
全等三角形与相似三角形性质比较
全等三角形 相似三角形
对应角相等 对应角相等
对应边相等 对应边的比等于相似比
对应高相等 对应高的比等于相似比
对应中线相等 对应中线的比等于相似比
对应角平分线相等 对应角平分线的比等于相似比
作业与拓展
1、教材P90-91:习题2、3、10
2、自学:教材P88:例1
谢 谢
