沪科版数学八年级上册 15.4 角平分线及其画法 课件(共22张PPT)
文档属性
| 名称 | 沪科版数学八年级上册 15.4 角平分线及其画法 课件(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-03 00:00:00 | ||
图片预览








文档简介
(共22张PPT)
§15.4.1 角的平分线
上海科学技术出版社 数学 八年级 上册
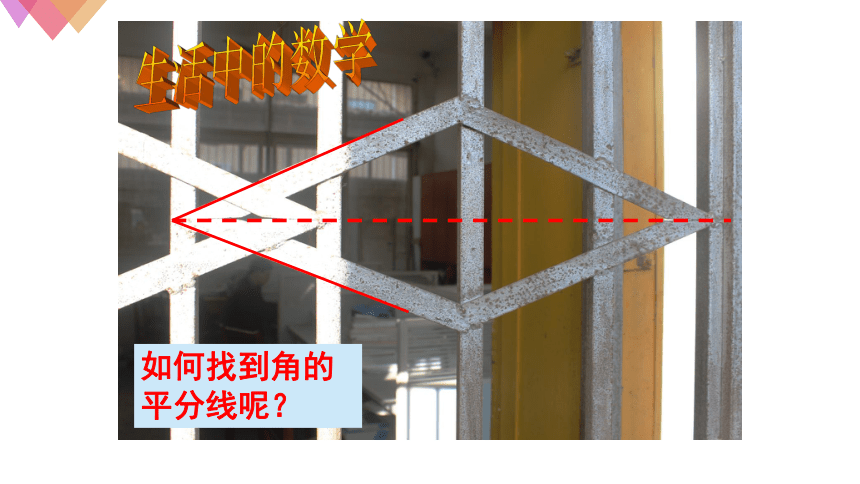
生活中的数学
生活中的数学
如何找到角的平分线呢?
会用尺规作图作角平分线,并会用语言描述作法。
通过操作、观察、证明所作射线是角平分线。
了解尺规作图的依据,会进行简单的应用。
学习目标
1.请任意画一个角,你能否作出角的平分线?
有哪些方法?
2.认真体会尺规作图法的步骤,思考:
① OM和ON有何数量关系?
② 为什么以大于 长为半径画弧?
③ 将作射线OP改为连接OP是否合理?
3.你能证明所作射线是角平分线吗?
自学课本
(141-143页)
当∠AOB的两边成一条直线时(即∠AOB =180°)你会用尺规作图法作这个角的平分线吗?这时的角平分线与直线AB有什么位置关系?
尝试练习
O
B
A
自学课本
1.请任意画一个角,你能否作出角的平分线?
有哪些方法?
2.认真体会尺规作图法的步骤,思考:
① OM和ON有何数量关系?
② 为什么以大于 长为半径画弧?
③ 将作射线OP改为连接OP是否合理?
3.你能证明所作射线是角平分线吗?
(141-143页)
师
友
对
议
尝试练习
当∠AOB的两边成一条直线时(即∠AOB =180°)你会用尺规作图法作这个角的平分线吗?这时的角平分线与直线AB有什么位置关系?
O
B
A
小
组
组
议
通过操作和自学课本,
你知道几种作角平分线的方法?
折叠法
度量法
尺规作图法
展示评讲
1、以点O为圆心,任意长为半径作弧,与角的两边分别交于M、N两点;
2、分别以M,N为圆心,大于 的长为半径在角的内部画弧交于点P;
3、作射线OP;
则射线OP就是所求作∠AOB的平分线。
A
B
M
N
P
O
角平分线的尺规作图。
作法:
展示评讲
B
A
N
M
P
O
连接PM,PN
在△OMP和△ONP中
OM=ON
MP=NP
OP=OP
∴ △OMP ≌ △ONP(SSS)
∴ ∠MOP = ∠NOP
即:OP平分∠AOB
证明:
展示评讲
∵
你能证明OP是角平分线吗?
展示评讲
B
A
O
E
D
F
OF⊥AB
1.当∠AOB=180°时
此时,角平分线与直线AB是垂直的关系
(合作探究)
巩固练习
发现问题:尝试练角的角平分线与平角所在直线垂直。
提出问题:如何经过一点作已知直线垂线?
方案设计:由于这一点可能在直线上或直线外,这个作图要分两种情况:
验 证:用折叠或测量的方法验证所作直线是否垂直直线AB。
证 明:所作直线是否垂直直线AB
2.经过已知直线外一点作这条
直线的垂线
已知:直线AB和AB外一点C
求作:AB的垂线,使它经过点C
作图:
B
A
C
1.经过已知直线上的一点作这条
直线的垂线
已知:直线AB和AB上一点C
求作:AB的垂线,使它经过点C
作图:
C
B
A
展示评讲
B
A
C
E
D
F
1.当C点在直线AB上时;
① 以C点为圆心,任意长为半径画弧交AB于D,E两点
CD=CE
C点在线段DE的垂直平分线上,
② 以D,E为圆心,大于 为半径画弧交于点F
FD=FE
F点在线段DE的垂直平分线上,
CF所在直线是线段DE的垂直平分线
即CF⊥AB
2.当C点在直线AB外时.
展示评讲
A
B
C
E
F
K
D
作法:
(1)任意取一点K,使K和C在AB的两旁;
(2)以点C为圆心,CK长为半径作弧,交AB于点D和E;
(3)分别以点D和点E为圆心,大于 的长为半径作弧,两弧交于点F;
(4)作直线CF.直线CF是所求的垂线。
展示评讲
A
B
C
E
F
K
D
已知:CD=CE,DF=EF
连接CD,CE, DF,EF
求证:CF⊥AB
证明:
∵CD=CE
∴C点在线段DE的垂直平分线上
∵DF=EF
∴F点在线段DE的垂直平分线上
∴CF是线段DE的垂直平分线
∴CF⊥DE,即CF⊥AB
当堂检测
A
B
C
已知:如图,在△ABC中,∠A=30°,∠B=60°。
(1)作∠B的平分线BD交AC于点D (30分) ;过D点作AB的垂线交AB于点E(20分)(要求:尺规作图,保留作图痕迹,不必写作法和证明);
(2)求证:△ADE ≌ △BDE。(50分)
(共100分)
当堂检测
A
B
C
D
E
证明:
∵DE⊥AB
∴ ∠AED=∠BED=90°
∵BD平分∠ABC,∠B=60°
∴ ∠DBE=30°
∵∠A=30°
∴ ∠A=∠DBE
在△ADE和△BDE中
DE=DE
∴ △ADE ≌ △BDE(AAS)
∠A=∠DBE
∠AED=∠BED
∵
师生总结
学生谈学习收获
通过本节课的学习,
我了解了......
我知道了......
我掌握了......
师生总结
角的
平分线
(知识树)
作角平分线的几种方法
生活中的角平分线
角平分线
的作法
直线的垂线作法
构建两个三角 形全等
尺规作图的
简单应用
角平分线
尺规作图
尺规作图的依据
同学们再见!
感谢聆听!
敬请批评与指正!
§15.4.1 角的平分线
上海科学技术出版社 数学 八年级 上册
生活中的数学
生活中的数学
如何找到角的平分线呢?
会用尺规作图作角平分线,并会用语言描述作法。
通过操作、观察、证明所作射线是角平分线。
了解尺规作图的依据,会进行简单的应用。
学习目标
1.请任意画一个角,你能否作出角的平分线?
有哪些方法?
2.认真体会尺规作图法的步骤,思考:
① OM和ON有何数量关系?
② 为什么以大于 长为半径画弧?
③ 将作射线OP改为连接OP是否合理?
3.你能证明所作射线是角平分线吗?
自学课本
(141-143页)
当∠AOB的两边成一条直线时(即∠AOB =180°)你会用尺规作图法作这个角的平分线吗?这时的角平分线与直线AB有什么位置关系?
尝试练习
O
B
A
自学课本
1.请任意画一个角,你能否作出角的平分线?
有哪些方法?
2.认真体会尺规作图法的步骤,思考:
① OM和ON有何数量关系?
② 为什么以大于 长为半径画弧?
③ 将作射线OP改为连接OP是否合理?
3.你能证明所作射线是角平分线吗?
(141-143页)
师
友
对
议
尝试练习
当∠AOB的两边成一条直线时(即∠AOB =180°)你会用尺规作图法作这个角的平分线吗?这时的角平分线与直线AB有什么位置关系?
O
B
A
小
组
组
议
通过操作和自学课本,
你知道几种作角平分线的方法?
折叠法
度量法
尺规作图法
展示评讲
1、以点O为圆心,任意长为半径作弧,与角的两边分别交于M、N两点;
2、分别以M,N为圆心,大于 的长为半径在角的内部画弧交于点P;
3、作射线OP;
则射线OP就是所求作∠AOB的平分线。
A
B
M
N
P
O
角平分线的尺规作图。
作法:
展示评讲
B
A
N
M
P
O
连接PM,PN
在△OMP和△ONP中
OM=ON
MP=NP
OP=OP
∴ △OMP ≌ △ONP(SSS)
∴ ∠MOP = ∠NOP
即:OP平分∠AOB
证明:
展示评讲
∵
你能证明OP是角平分线吗?
展示评讲
B
A
O
E
D
F
OF⊥AB
1.当∠AOB=180°时
此时,角平分线与直线AB是垂直的关系
(合作探究)
巩固练习
发现问题:尝试练角的角平分线与平角所在直线垂直。
提出问题:如何经过一点作已知直线垂线?
方案设计:由于这一点可能在直线上或直线外,这个作图要分两种情况:
验 证:用折叠或测量的方法验证所作直线是否垂直直线AB。
证 明:所作直线是否垂直直线AB
2.经过已知直线外一点作这条
直线的垂线
已知:直线AB和AB外一点C
求作:AB的垂线,使它经过点C
作图:
B
A
C
1.经过已知直线上的一点作这条
直线的垂线
已知:直线AB和AB上一点C
求作:AB的垂线,使它经过点C
作图:
C
B
A
展示评讲
B
A
C
E
D
F
1.当C点在直线AB上时;
① 以C点为圆心,任意长为半径画弧交AB于D,E两点
CD=CE
C点在线段DE的垂直平分线上,
② 以D,E为圆心,大于 为半径画弧交于点F
FD=FE
F点在线段DE的垂直平分线上,
CF所在直线是线段DE的垂直平分线
即CF⊥AB
2.当C点在直线AB外时.
展示评讲
A
B
C
E
F
K
D
作法:
(1)任意取一点K,使K和C在AB的两旁;
(2)以点C为圆心,CK长为半径作弧,交AB于点D和E;
(3)分别以点D和点E为圆心,大于 的长为半径作弧,两弧交于点F;
(4)作直线CF.直线CF是所求的垂线。
展示评讲
A
B
C
E
F
K
D
已知:CD=CE,DF=EF
连接CD,CE, DF,EF
求证:CF⊥AB
证明:
∵CD=CE
∴C点在线段DE的垂直平分线上
∵DF=EF
∴F点在线段DE的垂直平分线上
∴CF是线段DE的垂直平分线
∴CF⊥DE,即CF⊥AB
当堂检测
A
B
C
已知:如图,在△ABC中,∠A=30°,∠B=60°。
(1)作∠B的平分线BD交AC于点D (30分) ;过D点作AB的垂线交AB于点E(20分)(要求:尺规作图,保留作图痕迹,不必写作法和证明);
(2)求证:△ADE ≌ △BDE。(50分)
(共100分)
当堂检测
A
B
C
D
E
证明:
∵DE⊥AB
∴ ∠AED=∠BED=90°
∵BD平分∠ABC,∠B=60°
∴ ∠DBE=30°
∵∠A=30°
∴ ∠A=∠DBE
在△ADE和△BDE中
DE=DE
∴ △ADE ≌ △BDE(AAS)
∠A=∠DBE
∠AED=∠BED
∵
师生总结
学生谈学习收获
通过本节课的学习,
我了解了......
我知道了......
我掌握了......
师生总结
角的
平分线
(知识树)
作角平分线的几种方法
生活中的角平分线
角平分线
的作法
直线的垂线作法
构建两个三角 形全等
尺规作图的
简单应用
角平分线
尺规作图
尺规作图的依据
同学们再见!
感谢聆听!
敬请批评与指正!
