2021-2022学年人教版八年级数学上册13.1 轴对称 同步优化 (word版含解析)
文档属性
| 名称 | 2021-2022学年人教版八年级数学上册13.1 轴对称 同步优化 (word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 873.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-03 20:05:55 | ||
图片预览




文档简介
人教版 八年级数学 上册 13.1 轴对称 同步优化
一、选择题
1. 下列四个图形中,不是轴对称图形的是( )
2. P是∠AOB内一点,分别作点P关于直线OA,OB的对称点P1,P2,连接OP1,OP2,则下列结论正确的是 ( )
A. OP1⊥OP2 B. OP1=OP2
C. OP1⊥OP2且OP1=OP2 D. OP1≠OP2
3. 在汉字“生活中的日常用品”中,是轴对称图形的有 ( )
A.2个 B.3个 C.4个 D.5个
4. 已知:在平面直角坐标系中,A(a,b)(b≠0),B(m,n).若a-m=4,b+n=0,则下列结论正确的是( )
A.把点A向左平移4个单位长度后,与点B关于x轴对称
B.把点A向右平移4个单位长度后,与点B关于x轴对称
C.把点A向左平移4个单位长度后,与点B关于y轴对称
D.把点A向右平移4个单位长度后,与点B关于y轴对称
5. 如图,在△ABC中,点D在BC上,将点D分别以AB,AC为对称轴,画出对称点E,F,并连接AE,AF.根据图中标示的角度,∠EAF的度数为( )
A.113° B.124°
C.129° D.134°
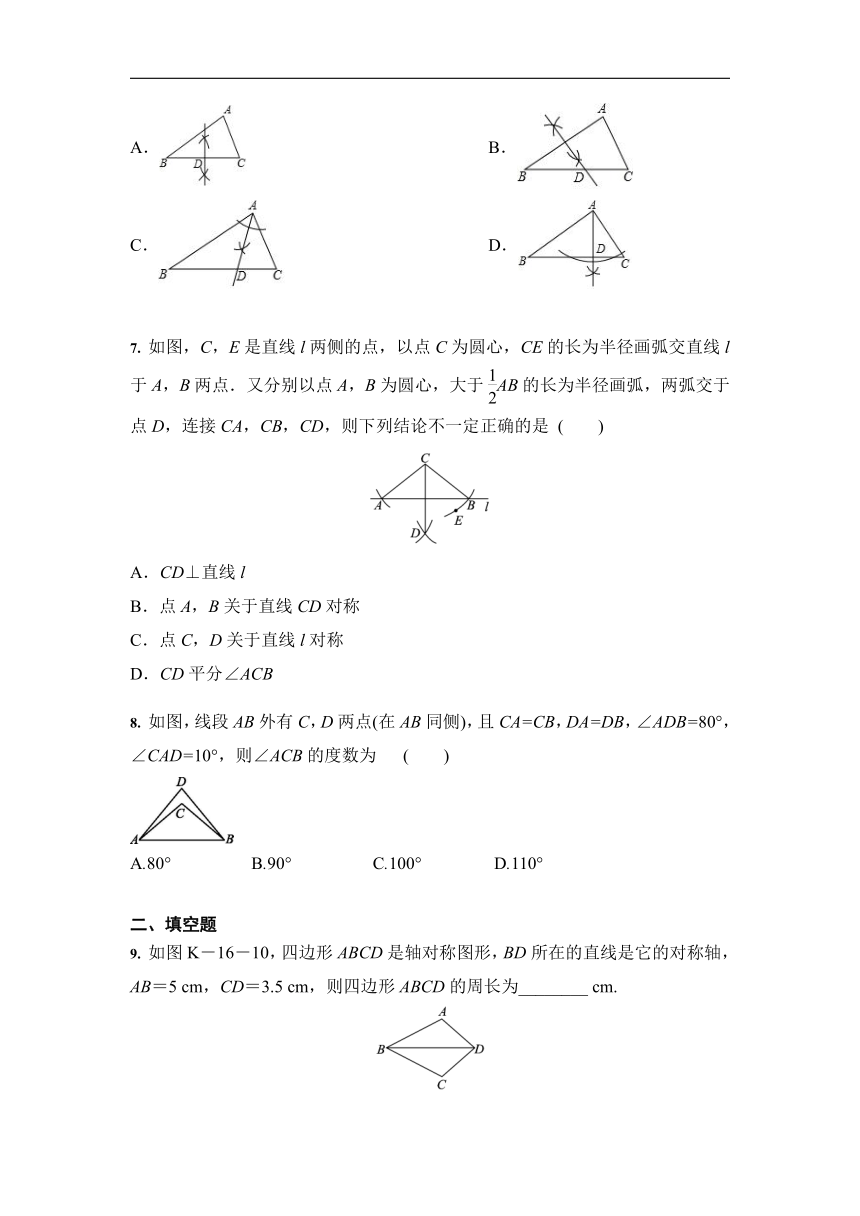
6. 通过如下尺规作图,能确定点是边中点的是
A. B.
C. D.
7. 如图,C,E是直线l两侧的点,以点C为圆心,CE的长为半径画弧交直线l于A,B两点.又分别以点A,B为圆心,大于AB的长为半径画弧,两弧交于点D,连接CA,CB,CD,则下列结论不一定正确的是 ( )
A.CD⊥直线l
B.点A,B关于直线CD对称
C.点C,D关于直线l对称
D.CD平分∠ACB
8. 如图,线段AB外有C,D两点(在AB同侧),且CA=CB,DA=DB,∠ADB=80°,∠CAD=10°,则∠ACB的度数为 ( )
A.80° B.90° C.100° D.110°
二、填空题
9. 如图K-16-10,四边形ABCD是轴对称图形,BD所在的直线是它的对称轴,AB=5 cm,CD=3.5 cm,则四边形ABCD的周长为________ cm.
10. 如图,△ABC中,AC=8,BC=5,AB的垂直平分线DE交AB于点D,交边AC于点E,则△BCE的周长为________.
11. 如图,点P在∠AOB内,M,N分别是点P关于OA,OB的对称点,连接MN交OA于点E,交OB于点F.若△PEF的周长是20 cm,则MN的长是________cm.
12. 设点P(2m-3,3-m)关于y轴的对称点在第二象限,则整数m的值为________.
13. 在平面直角坐标系中,点A的坐标是(-1,2).作点A关于x轴的对称点,得到点A1,再将点A1向下平移4个单位长度,得到点A2,则点A2的坐标是________.
14. 如图,在△ABC中,AB,AC的垂直平分线分别交BC于点E,F.若△AEF的周长为10 cm,则BC的长为 cm.
三、解答题
15. 把下列正多边形对称轴的条数填入表格中.
图形
正多边
形的边数 3 4 5 6 7 8
对称轴
的条数 ____ ____ ____ ____ ____ ____
根据上表,请你就一个正n边形对称轴的条数做一个猜想,写出猜想的结果.(不用证明)
16. 如图,在四边形ABCD中,AD∥BC,E是CD的中点,连接AE,BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)AD=FC;
(2)AB=BC+AD.
17. 如图,在△ABC中,AB边的垂直平分线DE分别与AB边和AC边交于点D和点E,BC边的垂直平分线FG分别与BC边和AC边交于点F和点G,若△BEG的周长为16,GE=3,求AC的长.
18. 已知:如图,∠BAC的平分线与BC的垂直平分线DG交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:BE=CF;
(2)若AF=6,BC=7,求△ABC的周长.
19. 如图,DF为△ABC的边BC的垂直平分线,F为垂足,DF交△ABC的外角平分线AD于点D,DE⊥AB于点E,且AB>AC,连接BD,CD.求证:
(1)∠DBE=∠DCA;
(2)BE=AC+AE.
人教版 八年级数学 上册 13.1 轴对称 同步优化-答案
一、选择题
1. 【答案】B
2. 【答案】 B
3. 【答案】B [解析] 根据轴对称图形的定义,在汉字“生活中的日常用品”中,是轴对称图形的有“中”“日”“品”3个.故选B.
4. 【答案】A [解析] ∵a-m=4,∴a-4=m.
又∵b+n=0(b≠0),∴b=-n.
∴把点A向左平移4个单位长度后,与点B关于x轴对称.
5. 【答案】D [解析] 连接AD.
∵点D分别以AB,AC为对称轴,画出对称点E,F,∴∠EAB=∠BAD,∠FAC=∠CAD.
∵∠B=62°,∠C=51°,
∴∠BAC=∠BAD+∠CAD=67°.
∴∠EAF=2∠BAC=134°.
6. 【答案】A
【解析】作线段的垂直平分线可得线段的中点.
由此可知:选项A符合条件,故选A.
7. 【答案】C [解析] 由作法可知CD垂直平分AB,
故选项A,B正确;
∵CD垂直平分AB,∴CA=CB.
设CD与AB交于点G,
易证Rt△ACG≌Rt△BCG,∴∠ACG=∠BCG,
即CD平分∠ACB,故选项D正确;
∵AB不一定平分CD,故选项C错误.
故选C.
8. 【答案】C
二、填空题
9. 【答案】17
10. 【答案】13 【解析】∵DE垂直平分AB,∴AE=BE,∵AE+EC=8,∴EC+BE=8,∴△BCE的周长为BE+EC+BC=13.
11. 【答案】20
12. 【答案】2 [解析] 由于点P关于y轴的对称点在第二象限,则点P在第一象限.
依题意有解得因为m为整数,所以m=2.
13. 【答案】(-1,-6) [解析] ∵点A的坐标是(-1,2),作点A关于x轴的对称点,得到点A1,
∴点A1的坐标是(-1,-2).
∵将点A1向下平移4个单位长度,得到点A2,
∴点A2的坐标是(-1,-6).
14. 【答案】10 [解析] ∵AB,AC的垂直平分线分别交BC于点E,F,∴AE=BE,AF=CF.
∴BC=BE+EF+CF=AE+EF+AF=10 cm.
三、解答题
15. 【答案】
解:3 4 5 6 7 8
猜想:一个正n边形有n条对称轴.
16. 【答案】
证明:(1)∵E是CD的中点,∴DE=CE.
∵AD∥BC,
∴∠ADE=∠FCE,∠DAE=∠CFE.
∴△ADE≌△FCE.∴AD=FC.
(2)∵△ADE≌△FCE,
∴AE=FE.
又∵BE⊥AE,∴BE垂直平分AF.
∴AB=FB.
∵FB=BC+FC=BC+AD,
∴AB=BC+AD.
17. 【答案】
解:∵DE垂直平分线段AB,GF垂直平分线段BC,
∴EB=EA,GB=GC.
∵△BEG的周长为16,
∴EB+GB+GE=16.
∴EA+GC+GE=16.
∴GA+GE+GE+GE+EC=16.
∴AC+2GE=16.
∵GE=3,
∴AC=10.
18. 【答案】
(1)证明:如图,连接CD.
∵点D在BC的垂直平分线上,∴BD=CD.
∵DE⊥AB,DF⊥AC,AD平分∠BAC,
∴DE=DF,∠BED=∠CFD=90°.
在Rt△BDE和Rt△CDF中,
∴Rt△BDE≌Rt△CDF(HL).∴BE=CF.
(2)在Rt△ADE和Rt△ADF中,
∴Rt△ADE≌Rt△ADF.
∴AE=AF=6.
∴△ABC的周长=AB+BC+AC=(AE+BE)+BC+(AF-CF)=6+7+6=19.
19. 【答案】
证明:(1)如图,过点D作DG⊥CA交CA的延长线于点G.
∵DF是BC的垂直平分线,∴BD=CD.
∵AD是△ABC的外角平分线,DE⊥AB,DG⊥CA,
∴DE=DG,∠DEB=∠DGC=90°.
在Rt△DBE和Rt△DCG中,
∴Rt△DBE≌Rt△DCG(HL).
∴∠DBE=∠DCA.
(2)∵Rt△DBE≌Rt△DCG,∴BE=CG.
在Rt△DEA和Rt△DGA中,
∴Rt△DEA≌Rt△DGA(HL).
∴AE=AG.
∴BE=CG=AC+AG=AC+AE,
即BE=AC+AE.
一、选择题
1. 下列四个图形中,不是轴对称图形的是( )
2. P是∠AOB内一点,分别作点P关于直线OA,OB的对称点P1,P2,连接OP1,OP2,则下列结论正确的是 ( )
A. OP1⊥OP2 B. OP1=OP2
C. OP1⊥OP2且OP1=OP2 D. OP1≠OP2
3. 在汉字“生活中的日常用品”中,是轴对称图形的有 ( )
A.2个 B.3个 C.4个 D.5个
4. 已知:在平面直角坐标系中,A(a,b)(b≠0),B(m,n).若a-m=4,b+n=0,则下列结论正确的是( )
A.把点A向左平移4个单位长度后,与点B关于x轴对称
B.把点A向右平移4个单位长度后,与点B关于x轴对称
C.把点A向左平移4个单位长度后,与点B关于y轴对称
D.把点A向右平移4个单位长度后,与点B关于y轴对称
5. 如图,在△ABC中,点D在BC上,将点D分别以AB,AC为对称轴,画出对称点E,F,并连接AE,AF.根据图中标示的角度,∠EAF的度数为( )
A.113° B.124°
C.129° D.134°
6. 通过如下尺规作图,能确定点是边中点的是
A. B.
C. D.
7. 如图,C,E是直线l两侧的点,以点C为圆心,CE的长为半径画弧交直线l于A,B两点.又分别以点A,B为圆心,大于AB的长为半径画弧,两弧交于点D,连接CA,CB,CD,则下列结论不一定正确的是 ( )
A.CD⊥直线l
B.点A,B关于直线CD对称
C.点C,D关于直线l对称
D.CD平分∠ACB
8. 如图,线段AB外有C,D两点(在AB同侧),且CA=CB,DA=DB,∠ADB=80°,∠CAD=10°,则∠ACB的度数为 ( )
A.80° B.90° C.100° D.110°
二、填空题
9. 如图K-16-10,四边形ABCD是轴对称图形,BD所在的直线是它的对称轴,AB=5 cm,CD=3.5 cm,则四边形ABCD的周长为________ cm.
10. 如图,△ABC中,AC=8,BC=5,AB的垂直平分线DE交AB于点D,交边AC于点E,则△BCE的周长为________.
11. 如图,点P在∠AOB内,M,N分别是点P关于OA,OB的对称点,连接MN交OA于点E,交OB于点F.若△PEF的周长是20 cm,则MN的长是________cm.
12. 设点P(2m-3,3-m)关于y轴的对称点在第二象限,则整数m的值为________.
13. 在平面直角坐标系中,点A的坐标是(-1,2).作点A关于x轴的对称点,得到点A1,再将点A1向下平移4个单位长度,得到点A2,则点A2的坐标是________.
14. 如图,在△ABC中,AB,AC的垂直平分线分别交BC于点E,F.若△AEF的周长为10 cm,则BC的长为 cm.
三、解答题
15. 把下列正多边形对称轴的条数填入表格中.
图形
正多边
形的边数 3 4 5 6 7 8
对称轴
的条数 ____ ____ ____ ____ ____ ____
根据上表,请你就一个正n边形对称轴的条数做一个猜想,写出猜想的结果.(不用证明)
16. 如图,在四边形ABCD中,AD∥BC,E是CD的中点,连接AE,BE,BE⊥AE,延长AE交BC的延长线于点F.
求证:(1)AD=FC;
(2)AB=BC+AD.
17. 如图,在△ABC中,AB边的垂直平分线DE分别与AB边和AC边交于点D和点E,BC边的垂直平分线FG分别与BC边和AC边交于点F和点G,若△BEG的周长为16,GE=3,求AC的长.
18. 已知:如图,∠BAC的平分线与BC的垂直平分线DG交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.
(1)求证:BE=CF;
(2)若AF=6,BC=7,求△ABC的周长.
19. 如图,DF为△ABC的边BC的垂直平分线,F为垂足,DF交△ABC的外角平分线AD于点D,DE⊥AB于点E,且AB>AC,连接BD,CD.求证:
(1)∠DBE=∠DCA;
(2)BE=AC+AE.
人教版 八年级数学 上册 13.1 轴对称 同步优化-答案
一、选择题
1. 【答案】B
2. 【答案】 B
3. 【答案】B [解析] 根据轴对称图形的定义,在汉字“生活中的日常用品”中,是轴对称图形的有“中”“日”“品”3个.故选B.
4. 【答案】A [解析] ∵a-m=4,∴a-4=m.
又∵b+n=0(b≠0),∴b=-n.
∴把点A向左平移4个单位长度后,与点B关于x轴对称.
5. 【答案】D [解析] 连接AD.
∵点D分别以AB,AC为对称轴,画出对称点E,F,∴∠EAB=∠BAD,∠FAC=∠CAD.
∵∠B=62°,∠C=51°,
∴∠BAC=∠BAD+∠CAD=67°.
∴∠EAF=2∠BAC=134°.
6. 【答案】A
【解析】作线段的垂直平分线可得线段的中点.
由此可知:选项A符合条件,故选A.
7. 【答案】C [解析] 由作法可知CD垂直平分AB,
故选项A,B正确;
∵CD垂直平分AB,∴CA=CB.
设CD与AB交于点G,
易证Rt△ACG≌Rt△BCG,∴∠ACG=∠BCG,
即CD平分∠ACB,故选项D正确;
∵AB不一定平分CD,故选项C错误.
故选C.
8. 【答案】C
二、填空题
9. 【答案】17
10. 【答案】13 【解析】∵DE垂直平分AB,∴AE=BE,∵AE+EC=8,∴EC+BE=8,∴△BCE的周长为BE+EC+BC=13.
11. 【答案】20
12. 【答案】2 [解析] 由于点P关于y轴的对称点在第二象限,则点P在第一象限.
依题意有解得
13. 【答案】(-1,-6) [解析] ∵点A的坐标是(-1,2),作点A关于x轴的对称点,得到点A1,
∴点A1的坐标是(-1,-2).
∵将点A1向下平移4个单位长度,得到点A2,
∴点A2的坐标是(-1,-6).
14. 【答案】10 [解析] ∵AB,AC的垂直平分线分别交BC于点E,F,∴AE=BE,AF=CF.
∴BC=BE+EF+CF=AE+EF+AF=10 cm.
三、解答题
15. 【答案】
解:3 4 5 6 7 8
猜想:一个正n边形有n条对称轴.
16. 【答案】
证明:(1)∵E是CD的中点,∴DE=CE.
∵AD∥BC,
∴∠ADE=∠FCE,∠DAE=∠CFE.
∴△ADE≌△FCE.∴AD=FC.
(2)∵△ADE≌△FCE,
∴AE=FE.
又∵BE⊥AE,∴BE垂直平分AF.
∴AB=FB.
∵FB=BC+FC=BC+AD,
∴AB=BC+AD.
17. 【答案】
解:∵DE垂直平分线段AB,GF垂直平分线段BC,
∴EB=EA,GB=GC.
∵△BEG的周长为16,
∴EB+GB+GE=16.
∴EA+GC+GE=16.
∴GA+GE+GE+GE+EC=16.
∴AC+2GE=16.
∵GE=3,
∴AC=10.
18. 【答案】
(1)证明:如图,连接CD.
∵点D在BC的垂直平分线上,∴BD=CD.
∵DE⊥AB,DF⊥AC,AD平分∠BAC,
∴DE=DF,∠BED=∠CFD=90°.
在Rt△BDE和Rt△CDF中,
∴Rt△BDE≌Rt△CDF(HL).∴BE=CF.
(2)在Rt△ADE和Rt△ADF中,
∴Rt△ADE≌Rt△ADF.
∴AE=AF=6.
∴△ABC的周长=AB+BC+AC=(AE+BE)+BC+(AF-CF)=6+7+6=19.
19. 【答案】
证明:(1)如图,过点D作DG⊥CA交CA的延长线于点G.
∵DF是BC的垂直平分线,∴BD=CD.
∵AD是△ABC的外角平分线,DE⊥AB,DG⊥CA,
∴DE=DG,∠DEB=∠DGC=90°.
在Rt△DBE和Rt△DCG中,
∴Rt△DBE≌Rt△DCG(HL).
∴∠DBE=∠DCA.
(2)∵Rt△DBE≌Rt△DCG,∴BE=CG.
在Rt△DEA和Rt△DGA中,
∴Rt△DEA≌Rt△DGA(HL).
∴AE=AG.
∴BE=CG=AC+AG=AC+AE,
即BE=AC+AE.
