2020-2021学年上海市黄浦区七年级(上)期末数学试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年上海市黄浦区七年级(上)期末数学试卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 628.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-02 07:28:08 | ||
图片预览


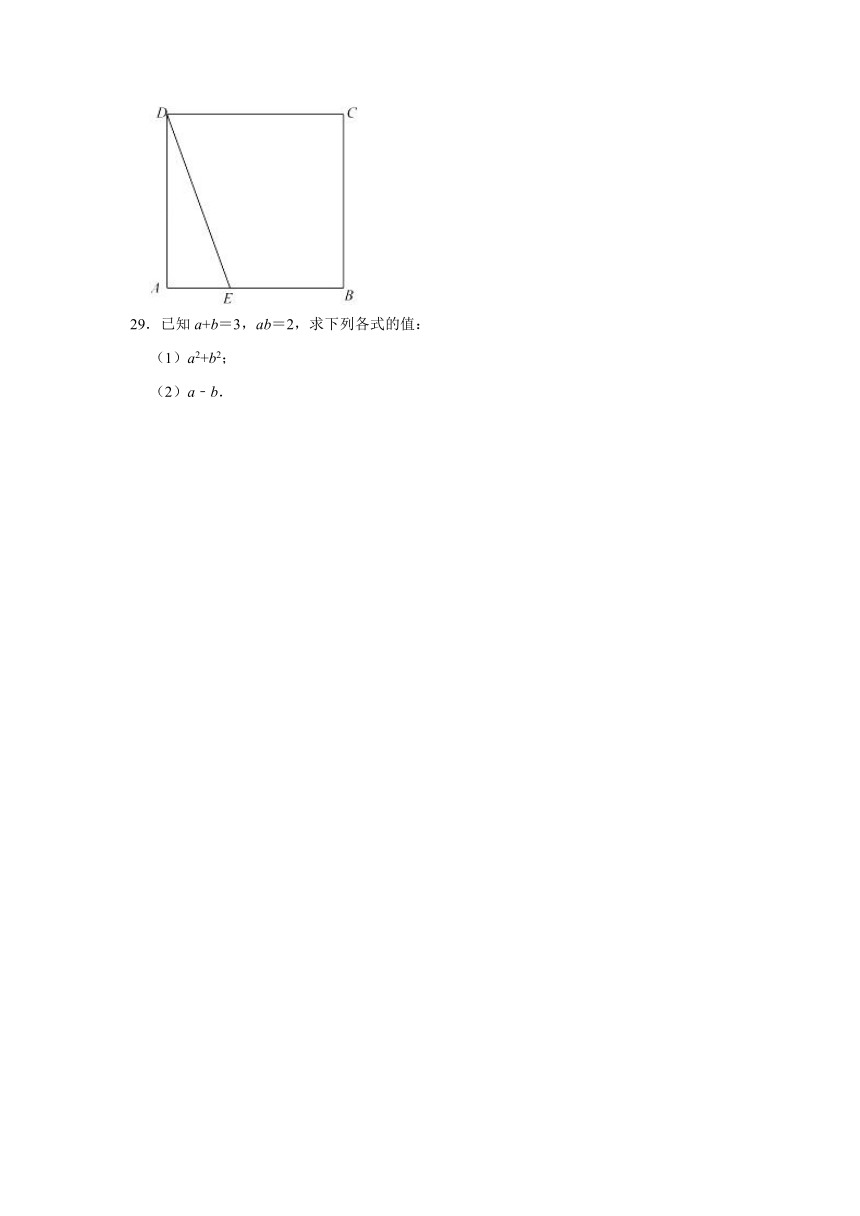

文档简介
2020-2021学年上海市黄浦区七年级第一学期期末数学试卷
一、选择题(每小题3分,共18分).
1.下列运算中,正确的是( )
A.a2+a2=a4 B.a6÷a2=a3
C.(a3b3)2=a9b9 D.a3 a2=a5
2.若x2+px+q=(x﹣3)(x+5),则p的值为( )
A.﹣15 B.﹣2 C.2 D.8
3.下列多项式中有因式x﹣1的是( )
①x2+x﹣2;②x2+3x+2;③x2﹣x﹣2;④x2﹣3x+2
A.①② B.②③ C.②④ D.①④
4.化简的结果是( )
A. B. C. D.1﹣x
5.如下所示的4组图形中,左边图形与右边图形成中心对称的有( )
A.1组 B.2组 C.3组 D.4组
6.如图,从边长为(2a+3)的正方形纸片中剪去一个边长为2a的正方形(a>0),剩余部分沿虚线剪开拼成一个长方形(不重叠无缝隙),那么长方形的面积为( )
A.4a2+6a B.6a+9 C.12a+9 D.12a+15
二、填空题(每小题2分,共24分):
7.用代数式表示“x的平方减去y的一半的差”: .
8.当x=﹣2时,代数式3x2﹣5x的值为 .
9.已知单项式与单项式3a2bm﹣2是同类项,则m+n= .
10.如果多项式x2﹣8x+a是一个完全平方式,那么a的值为 .
11.分解因式:x2﹣4x= .
12.计算:﹣24x6y3÷3x3y2= .
13.如果分式有意义,那么x的取值范围是 .
14.计算:= .
15.把0.0000306用科学记数法表示为: .
16.在正方形、等腰梯形、线段、等边三角形、平行四边形、圆这六种图形中,是旋转对称图形但不是中心对称图形的个数是 .
17.如图,将直角三角尺ABC(其中∠ABC=60°)绕点B顺时针旋转一个角度到A1BC1的位置,使得点A、B、C1在同一条直线上,如果AB的长度为10,那么点A转动到点A1走过的路程等于 .(结果保留π)
18.如图,将长方形ABCD按图中方式折叠,其中EF、EC为折痕,折叠后A1、B1、E在一直线上,已知∠BEC=65°,那么∠AEF的度数是 .
三、简答题(每小题5分,共30分):
19.计算:(x﹣1)2+(3+x)(3﹣x)﹣(x﹣2)(x+3).
20.计算:﹣22÷(π﹣3)0+()﹣3+(﹣1)﹣2.
21.分解因式:(x+3)(x﹣4)+6.
22.分解因式:a3﹣a2b﹣4a+4b.
23.计算:.
24.解方程:=1.
四、解答题(每小题6分,共18分):
25.先化简,再求值:(﹣)÷,其中a=﹣1.
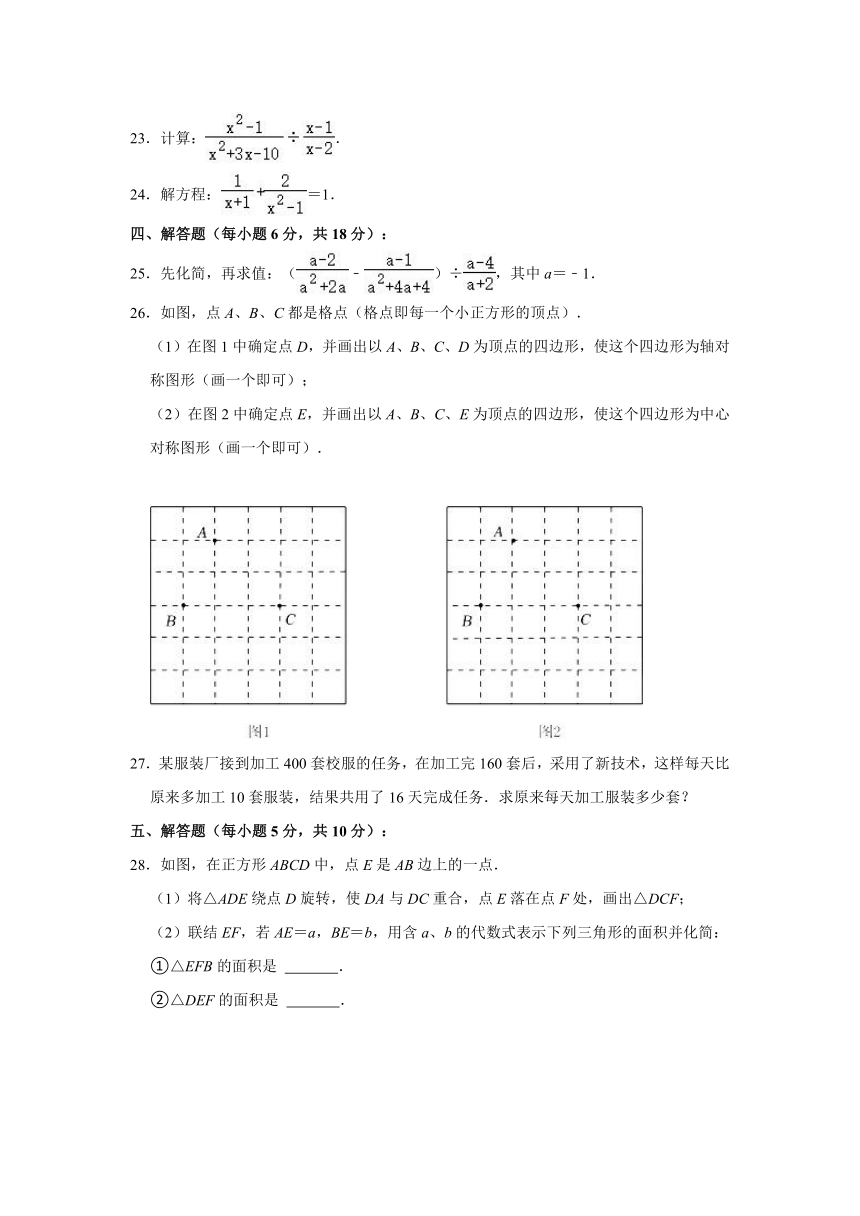
26.如图,点A、B、C都是格点(格点即每一个小正方形的顶点).
(1)在图1中确定点D,并画出以A、B、C、D为顶点的四边形,使这个四边形为轴对称图形(画一个即可);
(2)在图2中确定点E,并画出以A、B、C、E为顶点的四边形,使这个四边形为中心对称图形(画一个即可).
27.某服装厂接到加工400套校服的任务,在加工完160套后,采用了新技术,这样每天比原来多加工10套服装,结果共用了16天完成任务.求原来每天加工服装多少套?
五、解答题(每小题5分,共10分):
28.如图,在正方形ABCD中,点E是AB边上的一点.
(1)将△ADE绕点D旋转,使DA与DC重合,点E落在点F处,画出△DCF;
(2)联结EF,若AE=a,BE=b,用含a、b的代数式表示下列三角形的面积并化简:
①△EFB的面积是 .
②△DEF的面积是 .
29.已知a+b=3,ab=2,求下列各式的值:
(1)a2+b2;
(2)a﹣b.
参考答案
一、选择题(每小题3分,共18分).
1.下列运算中,正确的是( )
A.a2+a2=a4 B.a6÷a2=a3
C.(a3b3)2=a9b9 D.a3 a2=a5
【分析】选项A根据合并同类项法则判断即可,合并同类项的法则:把同类项的系数相加,所得结果作为系数,字母和字母的指数不变;
选项B根据同底数幂的除法法则判断即可,同底数幂的除法法则:底数不变,指数相减;
选项C根据积的乘方运算法则判断即可,积的乘方法则:把每一个因式分别乘方,再把所得的幂相乘;
选项D根据同底数幂的乘法法则判断即可,同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加.
解:A.a2+a2=2a2,故本选项不合题意;
B.a6÷a2=a4,故本选项不合题意;
C.(a3b3)2=a6b6,故本选项不合题意;
D.a3 a2=a5,故本选项符合题意;
故选:D.
2.若x2+px+q=(x﹣3)(x+5),则p的值为( )
A.﹣15 B.﹣2 C.2 D.8
【分析】根据十字相乘法的分解方法和特点可知:p=﹣3+5.
解:由x2+px+q=(x﹣3)(x+5)知,p=﹣3+5=2.
故选:C.
3.下列多项式中有因式x﹣1的是( )
①x2+x﹣2;②x2+3x+2;③x2﹣x﹣2;④x2﹣3x+2
A.①② B.②③ C.②④ D.①④
【分析】根据十字相乘法把各个多项式因式分解即可判断.
解:①x2+x﹣2=(x+2)(x﹣1);
②x2+3x+2=(x+1)(x+2);
③x2﹣x﹣2=(x+1)(x﹣2);
④x2﹣3x+2=(x﹣1)(x﹣2).
∴有因式x﹣1的是①④.
故选:D.
4.化简的结果是( )
A. B. C. D.1﹣x
【分析】约去分式的分子与分母的公因式即可.
解:,
故选:A.
5.如下所示的4组图形中,左边图形与右边图形成中心对称的有( )
A.1组 B.2组 C.3组 D.4组
【分析】欲分析两个图形是否成中心对称,主要把一个图形绕一个点旋转180°,观察是否能和另一个图形重合即可.
解:根据中心对称的概念,知①、②、③都是中心对称;④是轴对称.
故选:C.
6.如图,从边长为(2a+3)的正方形纸片中剪去一个边长为2a的正方形(a>0),剩余部分沿虚线剪开拼成一个长方形(不重叠无缝隙),那么长方形的面积为( )
A.4a2+6a B.6a+9 C.12a+9 D.12a+15
【分析】根据裁剪拼图可知,所拼成的长方形的长为(2a+3)+2a=4a+3,宽为(2a+3)﹣2a=3,由长方形面积的计算方法即可得出答案.
解:由题意可得,
所拼成的长方形的长为(2a+3)+2a=4a+3,宽为(2a+3)﹣2a=3,
所以长方形的面积为(4a+3)×3=12a+9,
故选:C.
二、填空题(每小题2分,共24分):
7.用代数式表示“x的平方减去y的一半的差”: x2﹣y .
【分析】根据题意,可以用代数式表示出“x的平方减去y的一半的差”.
解:“x的平方减去y的一半的差”可以表示为x2﹣y,
故答案为:x2﹣y.
8.当x=﹣2时,代数式3x2﹣5x的值为 22 .
【分析】把x=﹣2代入代数式计算即可得到结果.
解:把x=﹣2代入得:
原式=3×(﹣2)2﹣5×(﹣2)
=3×4﹣5×(﹣2)
=12+10
=22.
故答案为:22.
9.已知单项式与单项式3a2bm﹣2是同类项,则m+n= 6 .
【分析】根据同类项的概念求解.
解:∵单项式与单项式3a2bm﹣2是同类项,
∴n+1=2,m﹣2=3,
解得:n=1,m=5,
m+n=5+1=6.
故答案为:6.
10.如果多项式x2﹣8x+a是一个完全平方式,那么a的值为 16 .
【分析】利用完全平方公式的结构特征:常数项为一次项系数一半的平方,计算即可求出a的值.
解:∵多项式x2﹣8x+a是一个完全平方式,
∴a=()2=16.
故答案为:16.
11.分解因式:x2﹣4x= x(x﹣4) .
【分析】直接提取公因式x进而分解因式得出即可.
解:x2﹣4x=x(x﹣4).
故答案为:x(x﹣4).
12.计算:﹣24x6y3÷3x3y2= ﹣8x3y .
【分析】利用同底数幂的除法法则运算.
解:原式=﹣8x3y.
故答案为:﹣8x3y.
13.如果分式有意义,那么x的取值范围是 x≠﹣5 .
【分析】根据分式有意义的条件可得x+5≠0,再解之即可得出答案.
解:由题意得:x+5≠0,
解得:x≠﹣5,
故答案为:x≠﹣5.
14.计算:= .
【分析】原式通分并利用同分母分式的减法法则计算,即可得到结果.
解:原式=﹣==.
故答案为:.
15.把0.0000306用科学记数法表示为: 3.06×10﹣5 .
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
解:0.0000306=3.06×10﹣5.
故答案为:3.06×10﹣5.
16.在正方形、等腰梯形、线段、等边三角形、平行四边形、圆这六种图形中,是旋转对称图形但不是中心对称图形的个数是 1个 .
【分析】根据中心对称图形的定义以及旋转图形的性质分别判断得出即可.
解:正方形、等腰梯形、线段、等边三角形、平行四边形、圆这六种图形中,正方形、线段、平行四边形、圆都是中心对称图形,
只有等边三角形是旋转对称图形但不是中心对称图形,
故答案为:1个.
17.如图,将直角三角尺ABC(其中∠ABC=60°)绕点B顺时针旋转一个角度到A1BC1的位置,使得点A、B、C1在同一条直线上,如果AB的长度为10,那么点A转动到点A1走过的路程等于 π .(结果保留π)
【分析】根据三角尺的度数以及旋转的性质求出∠ABC=∠A′BC′=60°,然后根据平角等于180°求出∠ABA′,然后根据弧长公式列式进行计算即可得解.
解:∵∠A=30°,∠C=90°,△A′BC′是△ABC旋转得到,
∴∠ABC=∠A′BC′=60°,
∴∠ABA′=180°﹣∠A′BC′=180°﹣60°=120°,
∵AB的长度为10,
∴点A转动到点A1走过的路程==π.
故答案为:π.
18.如图,将长方形ABCD按图中方式折叠,其中EF、EC为折痕,折叠后A1、B1、E在一直线上,已知∠BEC=65°,那么∠AEF的度数是 25° .
【分析】利用翻折变换的性质即可解决.
解:由折叠可知,∠A1EF=∠AEF,∠A1EC=∠BEC=65°,
∵∠A1EF+∠AEF+∠A1EC+∠BEC=180°,
∴∠A1EF+∠AEF=50°,
∴∠AEF=25°,
故答案为:25°.
三、简答题(每小题5分,共30分):
19.计算:(x﹣1)2+(3+x)(3﹣x)﹣(x﹣2)(x+3).
【分析】先算乘方,再算乘法,合并解答即可.
解:(x﹣1)2+(3+x)(3﹣x)﹣(x﹣2)(x+3)
=x2﹣2x+1+9﹣x2﹣(x2+x﹣6)
=x2﹣2x+1+9﹣x2﹣x2﹣x+6
=﹣x2﹣3x+16.
20.计算:﹣22÷(π﹣3)0+()﹣3+(﹣1)﹣2.
【分析】根据零指数幂的意义以及负整数指数幂的意义即可求出答案.
解:原式=﹣4÷1+8+1=5
21.分解因式:(x+3)(x﹣4)+6.
【分析】先去括号,然后利用十字相乘法进行因式分解.
解:(x+3)(x﹣4)+6
=x2﹣x﹣12+6
=x2﹣x﹣6
=(x﹣3)(x+2).
22.分解因式:a3﹣a2b﹣4a+4b.
【分析】先分组,再提公因式,最后用平方差公式进一步进行因式分解.
解:a3﹣a2b﹣4a+4b
=(a3﹣4a)﹣(a2b﹣4b)
=a(a2﹣4)﹣b(a2﹣4)
=(a﹣b)(a2﹣4)
=(a﹣b)(a+2)(a﹣2).
23.计算:.
【分析】先把各个分式的分子、分母因式分解,根据分式的除法法则、约分法则计算即可.
解:原式=
=.
24.解方程:=1.
【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解:去分母得:x﹣1+2=x2﹣1,
整理得:x2﹣x﹣2=0,即(x﹣2)(x+1)=0,
解得 x=﹣1或x=2,
经检验:x=﹣1是增根,舍去;
x=2是原方程的根,
∴原方程的根是x=2.
四、解答题(每小题6分,共18分):
25.先化简,再求值:(﹣)÷,其中a=﹣1.
【分析】先算括号内的减法,再把除法变成乘法,求出结果,最后代入求出即可.
解:原式=[﹣]÷
=[﹣]÷
=
=,
当a=﹣1时,原式==﹣1.
26.如图,点A、B、C都是格点(格点即每一个小正方形的顶点).
(1)在图1中确定点D,并画出以A、B、C、D为顶点的四边形,使这个四边形为轴对称图形(画一个即可);
(2)在图2中确定点E,并画出以A、B、C、E为顶点的四边形,使这个四边形为中心对称图形(画一个即可).
【分析】(1)直接利用轴对称图形的性质得出一个符合题意的图形;
(2)直接利用中心对称图形的性质得出一个符合题意的图形即可.
解:(1)如图1所示:四边形ABCD即为所求;
(2)如图2所示:四边形ABCE即为所求.
27.某服装厂接到加工400套校服的任务,在加工完160套后,采用了新技术,这样每天比原来多加工10套服装,结果共用了16天完成任务.求原来每天加工服装多少套?
【分析】设原来每天加工服装x套,则采用了新技术后每天加工服装(x+10)套,利用工作时间=工作总量÷工作效率,结合共用了16天完成任务,即可得出关于x的分式方程,解之经检验后即可得出结论.
解:设原来每天加工服装x套,则采用了新技术后每天加工服装(x+10)套,
依题意得:+=16,
化简得:x2﹣15x﹣100=0,
解得:x1=20,x2=﹣5,
经检验,x1=20,x2=﹣5是原方程的解,但x2=﹣5不符合题意,舍去.
答:原来每天加工服装20套.
五、解答题(每小题5分,共10分):
28.如图,在正方形ABCD中,点E是AB边上的一点.
(1)将△ADE绕点D旋转,使DA与DC重合,点E落在点F处,画出△DCF;
(2)联结EF,若AE=a,BE=b,用含a、b的代数式表示下列三角形的面积并化简:
①△EFB的面积是 ab+b2 .
②△DEF的面积是 a2+ab+b2 .
【分析】(1)根据旋转的性质即可得到结论;
(2)根据正方形的性质得到AD=AB=BC=a+b,根据旋转的性质得到CF=AE=a,∠DCF=90°,DE=DF,∠CDF=∠ADE,推出B,C,F三点共线,①根据三角形的面积公式即可得到△EFB的面积;②根据勾股定理得到DE==,根据三角形的面积公式即可得到结论.
解:(1)如图所示,△DCF即为所求;
(2)∵AE=a,BE=b,
∴AB=a+b,
∵四边形ABCD是正方形,
∴AD=AB=BC=a+b,
∵将△ADE绕点D旋转得到△DCF,
∴CF=AE=a,∠DCF=90°,DE=DF,∠CDF=∠ADE,
∵∠DCB=90°,
∴∠BCF=180°,
∴B,C,F三点共线,
①△EFB的面积是BF BE=(a+b+a) b=ab+b2;
②∵∠ADC=90°,
∴∠EDF=90°,
∵DE==,
∴△DEF的面积是DE DF=××,
=a2+ab+b2;
故答案为:ab+b2;a2+ab+b2.
29.已知a+b=3,ab=2,求下列各式的值:
(1)a2+b2;
(2)a﹣b.
【分析】(1)根据完全平方公式变形,再代入求出即可;
(2)先求出(a﹣b)2的值,即可求出答案.
解:(1)∵a+b=3,ab=2,
∴a2+b2=(a+b)2﹣2ab=32﹣2×2=5;
(2)∵a+b=3,ab=2,
∴a﹣b=±=±=±=1.
一、选择题(每小题3分,共18分).
1.下列运算中,正确的是( )
A.a2+a2=a4 B.a6÷a2=a3
C.(a3b3)2=a9b9 D.a3 a2=a5
2.若x2+px+q=(x﹣3)(x+5),则p的值为( )
A.﹣15 B.﹣2 C.2 D.8
3.下列多项式中有因式x﹣1的是( )
①x2+x﹣2;②x2+3x+2;③x2﹣x﹣2;④x2﹣3x+2
A.①② B.②③ C.②④ D.①④
4.化简的结果是( )
A. B. C. D.1﹣x
5.如下所示的4组图形中,左边图形与右边图形成中心对称的有( )
A.1组 B.2组 C.3组 D.4组
6.如图,从边长为(2a+3)的正方形纸片中剪去一个边长为2a的正方形(a>0),剩余部分沿虚线剪开拼成一个长方形(不重叠无缝隙),那么长方形的面积为( )
A.4a2+6a B.6a+9 C.12a+9 D.12a+15
二、填空题(每小题2分,共24分):
7.用代数式表示“x的平方减去y的一半的差”: .
8.当x=﹣2时,代数式3x2﹣5x的值为 .
9.已知单项式与单项式3a2bm﹣2是同类项,则m+n= .
10.如果多项式x2﹣8x+a是一个完全平方式,那么a的值为 .
11.分解因式:x2﹣4x= .
12.计算:﹣24x6y3÷3x3y2= .
13.如果分式有意义,那么x的取值范围是 .
14.计算:= .
15.把0.0000306用科学记数法表示为: .
16.在正方形、等腰梯形、线段、等边三角形、平行四边形、圆这六种图形中,是旋转对称图形但不是中心对称图形的个数是 .
17.如图,将直角三角尺ABC(其中∠ABC=60°)绕点B顺时针旋转一个角度到A1BC1的位置,使得点A、B、C1在同一条直线上,如果AB的长度为10,那么点A转动到点A1走过的路程等于 .(结果保留π)
18.如图,将长方形ABCD按图中方式折叠,其中EF、EC为折痕,折叠后A1、B1、E在一直线上,已知∠BEC=65°,那么∠AEF的度数是 .
三、简答题(每小题5分,共30分):
19.计算:(x﹣1)2+(3+x)(3﹣x)﹣(x﹣2)(x+3).
20.计算:﹣22÷(π﹣3)0+()﹣3+(﹣1)﹣2.
21.分解因式:(x+3)(x﹣4)+6.
22.分解因式:a3﹣a2b﹣4a+4b.
23.计算:.
24.解方程:=1.
四、解答题(每小题6分,共18分):
25.先化简,再求值:(﹣)÷,其中a=﹣1.
26.如图,点A、B、C都是格点(格点即每一个小正方形的顶点).
(1)在图1中确定点D,并画出以A、B、C、D为顶点的四边形,使这个四边形为轴对称图形(画一个即可);
(2)在图2中确定点E,并画出以A、B、C、E为顶点的四边形,使这个四边形为中心对称图形(画一个即可).
27.某服装厂接到加工400套校服的任务,在加工完160套后,采用了新技术,这样每天比原来多加工10套服装,结果共用了16天完成任务.求原来每天加工服装多少套?
五、解答题(每小题5分,共10分):
28.如图,在正方形ABCD中,点E是AB边上的一点.
(1)将△ADE绕点D旋转,使DA与DC重合,点E落在点F处,画出△DCF;
(2)联结EF,若AE=a,BE=b,用含a、b的代数式表示下列三角形的面积并化简:
①△EFB的面积是 .
②△DEF的面积是 .
29.已知a+b=3,ab=2,求下列各式的值:
(1)a2+b2;
(2)a﹣b.
参考答案
一、选择题(每小题3分,共18分).
1.下列运算中,正确的是( )
A.a2+a2=a4 B.a6÷a2=a3
C.(a3b3)2=a9b9 D.a3 a2=a5
【分析】选项A根据合并同类项法则判断即可,合并同类项的法则:把同类项的系数相加,所得结果作为系数,字母和字母的指数不变;
选项B根据同底数幂的除法法则判断即可,同底数幂的除法法则:底数不变,指数相减;
选项C根据积的乘方运算法则判断即可,积的乘方法则:把每一个因式分别乘方,再把所得的幂相乘;
选项D根据同底数幂的乘法法则判断即可,同底数幂的乘法法则:同底数幂相乘,底数不变,指数相加.
解:A.a2+a2=2a2,故本选项不合题意;
B.a6÷a2=a4,故本选项不合题意;
C.(a3b3)2=a6b6,故本选项不合题意;
D.a3 a2=a5,故本选项符合题意;
故选:D.
2.若x2+px+q=(x﹣3)(x+5),则p的值为( )
A.﹣15 B.﹣2 C.2 D.8
【分析】根据十字相乘法的分解方法和特点可知:p=﹣3+5.
解:由x2+px+q=(x﹣3)(x+5)知,p=﹣3+5=2.
故选:C.
3.下列多项式中有因式x﹣1的是( )
①x2+x﹣2;②x2+3x+2;③x2﹣x﹣2;④x2﹣3x+2
A.①② B.②③ C.②④ D.①④
【分析】根据十字相乘法把各个多项式因式分解即可判断.
解:①x2+x﹣2=(x+2)(x﹣1);
②x2+3x+2=(x+1)(x+2);
③x2﹣x﹣2=(x+1)(x﹣2);
④x2﹣3x+2=(x﹣1)(x﹣2).
∴有因式x﹣1的是①④.
故选:D.
4.化简的结果是( )
A. B. C. D.1﹣x
【分析】约去分式的分子与分母的公因式即可.
解:,
故选:A.
5.如下所示的4组图形中,左边图形与右边图形成中心对称的有( )
A.1组 B.2组 C.3组 D.4组
【分析】欲分析两个图形是否成中心对称,主要把一个图形绕一个点旋转180°,观察是否能和另一个图形重合即可.
解:根据中心对称的概念,知①、②、③都是中心对称;④是轴对称.
故选:C.
6.如图,从边长为(2a+3)的正方形纸片中剪去一个边长为2a的正方形(a>0),剩余部分沿虚线剪开拼成一个长方形(不重叠无缝隙),那么长方形的面积为( )
A.4a2+6a B.6a+9 C.12a+9 D.12a+15
【分析】根据裁剪拼图可知,所拼成的长方形的长为(2a+3)+2a=4a+3,宽为(2a+3)﹣2a=3,由长方形面积的计算方法即可得出答案.
解:由题意可得,
所拼成的长方形的长为(2a+3)+2a=4a+3,宽为(2a+3)﹣2a=3,
所以长方形的面积为(4a+3)×3=12a+9,
故选:C.
二、填空题(每小题2分,共24分):
7.用代数式表示“x的平方减去y的一半的差”: x2﹣y .
【分析】根据题意,可以用代数式表示出“x的平方减去y的一半的差”.
解:“x的平方减去y的一半的差”可以表示为x2﹣y,
故答案为:x2﹣y.
8.当x=﹣2时,代数式3x2﹣5x的值为 22 .
【分析】把x=﹣2代入代数式计算即可得到结果.
解:把x=﹣2代入得:
原式=3×(﹣2)2﹣5×(﹣2)
=3×4﹣5×(﹣2)
=12+10
=22.
故答案为:22.
9.已知单项式与单项式3a2bm﹣2是同类项,则m+n= 6 .
【分析】根据同类项的概念求解.
解:∵单项式与单项式3a2bm﹣2是同类项,
∴n+1=2,m﹣2=3,
解得:n=1,m=5,
m+n=5+1=6.
故答案为:6.
10.如果多项式x2﹣8x+a是一个完全平方式,那么a的值为 16 .
【分析】利用完全平方公式的结构特征:常数项为一次项系数一半的平方,计算即可求出a的值.
解:∵多项式x2﹣8x+a是一个完全平方式,
∴a=()2=16.
故答案为:16.
11.分解因式:x2﹣4x= x(x﹣4) .
【分析】直接提取公因式x进而分解因式得出即可.
解:x2﹣4x=x(x﹣4).
故答案为:x(x﹣4).
12.计算:﹣24x6y3÷3x3y2= ﹣8x3y .
【分析】利用同底数幂的除法法则运算.
解:原式=﹣8x3y.
故答案为:﹣8x3y.
13.如果分式有意义,那么x的取值范围是 x≠﹣5 .
【分析】根据分式有意义的条件可得x+5≠0,再解之即可得出答案.
解:由题意得:x+5≠0,
解得:x≠﹣5,
故答案为:x≠﹣5.
14.计算:= .
【分析】原式通分并利用同分母分式的减法法则计算,即可得到结果.
解:原式=﹣==.
故答案为:.
15.把0.0000306用科学记数法表示为: 3.06×10﹣5 .
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负指数幂,指数由原数左边起第一个不为零的数字前面的0的个数所决定.
解:0.0000306=3.06×10﹣5.
故答案为:3.06×10﹣5.
16.在正方形、等腰梯形、线段、等边三角形、平行四边形、圆这六种图形中,是旋转对称图形但不是中心对称图形的个数是 1个 .
【分析】根据中心对称图形的定义以及旋转图形的性质分别判断得出即可.
解:正方形、等腰梯形、线段、等边三角形、平行四边形、圆这六种图形中,正方形、线段、平行四边形、圆都是中心对称图形,
只有等边三角形是旋转对称图形但不是中心对称图形,
故答案为:1个.
17.如图,将直角三角尺ABC(其中∠ABC=60°)绕点B顺时针旋转一个角度到A1BC1的位置,使得点A、B、C1在同一条直线上,如果AB的长度为10,那么点A转动到点A1走过的路程等于 π .(结果保留π)
【分析】根据三角尺的度数以及旋转的性质求出∠ABC=∠A′BC′=60°,然后根据平角等于180°求出∠ABA′,然后根据弧长公式列式进行计算即可得解.
解:∵∠A=30°,∠C=90°,△A′BC′是△ABC旋转得到,
∴∠ABC=∠A′BC′=60°,
∴∠ABA′=180°﹣∠A′BC′=180°﹣60°=120°,
∵AB的长度为10,
∴点A转动到点A1走过的路程==π.
故答案为:π.
18.如图,将长方形ABCD按图中方式折叠,其中EF、EC为折痕,折叠后A1、B1、E在一直线上,已知∠BEC=65°,那么∠AEF的度数是 25° .
【分析】利用翻折变换的性质即可解决.
解:由折叠可知,∠A1EF=∠AEF,∠A1EC=∠BEC=65°,
∵∠A1EF+∠AEF+∠A1EC+∠BEC=180°,
∴∠A1EF+∠AEF=50°,
∴∠AEF=25°,
故答案为:25°.
三、简答题(每小题5分,共30分):
19.计算:(x﹣1)2+(3+x)(3﹣x)﹣(x﹣2)(x+3).
【分析】先算乘方,再算乘法,合并解答即可.
解:(x﹣1)2+(3+x)(3﹣x)﹣(x﹣2)(x+3)
=x2﹣2x+1+9﹣x2﹣(x2+x﹣6)
=x2﹣2x+1+9﹣x2﹣x2﹣x+6
=﹣x2﹣3x+16.
20.计算:﹣22÷(π﹣3)0+()﹣3+(﹣1)﹣2.
【分析】根据零指数幂的意义以及负整数指数幂的意义即可求出答案.
解:原式=﹣4÷1+8+1=5
21.分解因式:(x+3)(x﹣4)+6.
【分析】先去括号,然后利用十字相乘法进行因式分解.
解:(x+3)(x﹣4)+6
=x2﹣x﹣12+6
=x2﹣x﹣6
=(x﹣3)(x+2).
22.分解因式:a3﹣a2b﹣4a+4b.
【分析】先分组,再提公因式,最后用平方差公式进一步进行因式分解.
解:a3﹣a2b﹣4a+4b
=(a3﹣4a)﹣(a2b﹣4b)
=a(a2﹣4)﹣b(a2﹣4)
=(a﹣b)(a2﹣4)
=(a﹣b)(a+2)(a﹣2).
23.计算:.
【分析】先把各个分式的分子、分母因式分解,根据分式的除法法则、约分法则计算即可.
解:原式=
=.
24.解方程:=1.
【分析】分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解:去分母得:x﹣1+2=x2﹣1,
整理得:x2﹣x﹣2=0,即(x﹣2)(x+1)=0,
解得 x=﹣1或x=2,
经检验:x=﹣1是增根,舍去;
x=2是原方程的根,
∴原方程的根是x=2.
四、解答题(每小题6分,共18分):
25.先化简,再求值:(﹣)÷,其中a=﹣1.
【分析】先算括号内的减法,再把除法变成乘法,求出结果,最后代入求出即可.
解:原式=[﹣]÷
=[﹣]÷
=
=,
当a=﹣1时,原式==﹣1.
26.如图,点A、B、C都是格点(格点即每一个小正方形的顶点).
(1)在图1中确定点D,并画出以A、B、C、D为顶点的四边形,使这个四边形为轴对称图形(画一个即可);
(2)在图2中确定点E,并画出以A、B、C、E为顶点的四边形,使这个四边形为中心对称图形(画一个即可).
【分析】(1)直接利用轴对称图形的性质得出一个符合题意的图形;
(2)直接利用中心对称图形的性质得出一个符合题意的图形即可.
解:(1)如图1所示:四边形ABCD即为所求;
(2)如图2所示:四边形ABCE即为所求.
27.某服装厂接到加工400套校服的任务,在加工完160套后,采用了新技术,这样每天比原来多加工10套服装,结果共用了16天完成任务.求原来每天加工服装多少套?
【分析】设原来每天加工服装x套,则采用了新技术后每天加工服装(x+10)套,利用工作时间=工作总量÷工作效率,结合共用了16天完成任务,即可得出关于x的分式方程,解之经检验后即可得出结论.
解:设原来每天加工服装x套,则采用了新技术后每天加工服装(x+10)套,
依题意得:+=16,
化简得:x2﹣15x﹣100=0,
解得:x1=20,x2=﹣5,
经检验,x1=20,x2=﹣5是原方程的解,但x2=﹣5不符合题意,舍去.
答:原来每天加工服装20套.
五、解答题(每小题5分,共10分):
28.如图,在正方形ABCD中,点E是AB边上的一点.
(1)将△ADE绕点D旋转,使DA与DC重合,点E落在点F处,画出△DCF;
(2)联结EF,若AE=a,BE=b,用含a、b的代数式表示下列三角形的面积并化简:
①△EFB的面积是 ab+b2 .
②△DEF的面积是 a2+ab+b2 .
【分析】(1)根据旋转的性质即可得到结论;
(2)根据正方形的性质得到AD=AB=BC=a+b,根据旋转的性质得到CF=AE=a,∠DCF=90°,DE=DF,∠CDF=∠ADE,推出B,C,F三点共线,①根据三角形的面积公式即可得到△EFB的面积;②根据勾股定理得到DE==,根据三角形的面积公式即可得到结论.
解:(1)如图所示,△DCF即为所求;
(2)∵AE=a,BE=b,
∴AB=a+b,
∵四边形ABCD是正方形,
∴AD=AB=BC=a+b,
∵将△ADE绕点D旋转得到△DCF,
∴CF=AE=a,∠DCF=90°,DE=DF,∠CDF=∠ADE,
∵∠DCB=90°,
∴∠BCF=180°,
∴B,C,F三点共线,
①△EFB的面积是BF BE=(a+b+a) b=ab+b2;
②∵∠ADC=90°,
∴∠EDF=90°,
∵DE==,
∴△DEF的面积是DE DF=××,
=a2+ab+b2;
故答案为:ab+b2;a2+ab+b2.
29.已知a+b=3,ab=2,求下列各式的值:
(1)a2+b2;
(2)a﹣b.
【分析】(1)根据完全平方公式变形,再代入求出即可;
(2)先求出(a﹣b)2的值,即可求出答案.
解:(1)∵a+b=3,ab=2,
∴a2+b2=(a+b)2﹣2ab=32﹣2×2=5;
(2)∵a+b=3,ab=2,
∴a﹣b=±=±=±=1.
同课章节目录
