28.2解直角三角形的应用 同步练习卷2021- 2022学年人教版数学九年级下册(word版 含答案)
文档属性
| 名称 | 28.2解直角三角形的应用 同步练习卷2021- 2022学年人教版数学九年级下册(word版 含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 269.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-04 08:14:56 | ||
图片预览



文档简介
2022年人教版数学九年级下册
《解直角三角形的应用》同步练习卷
一、选择题
如图,在地面上的点A处测得树顶B的仰角为α度,AC=7 m,则树高BC为(用含α的代数式表示)( )
A.7sinα B.7cosα C.7tanα D.
如图,为了测量河两岸A、B两点的距离,在与AB垂直的方向点C处测得AC=a,
∠ACB=α,那么AB=( )
A.asinα B.atanα C.acosα D.
如图,A,B两点在河的两岸,要测量这两点之间的距离,测量者在与A同侧的河岸边选定一点C,测出AC=a米,∠BAC=90°,∠ACB=40°,则AB等于( )
A.asin40°米 B.acos40°米 C.atan40°米 D.米
某简易房示意图如图所示,它是一个轴对称图形,则坡屋顶上弦杆AB的长为( )
A.米 B.米 C.米 D.米
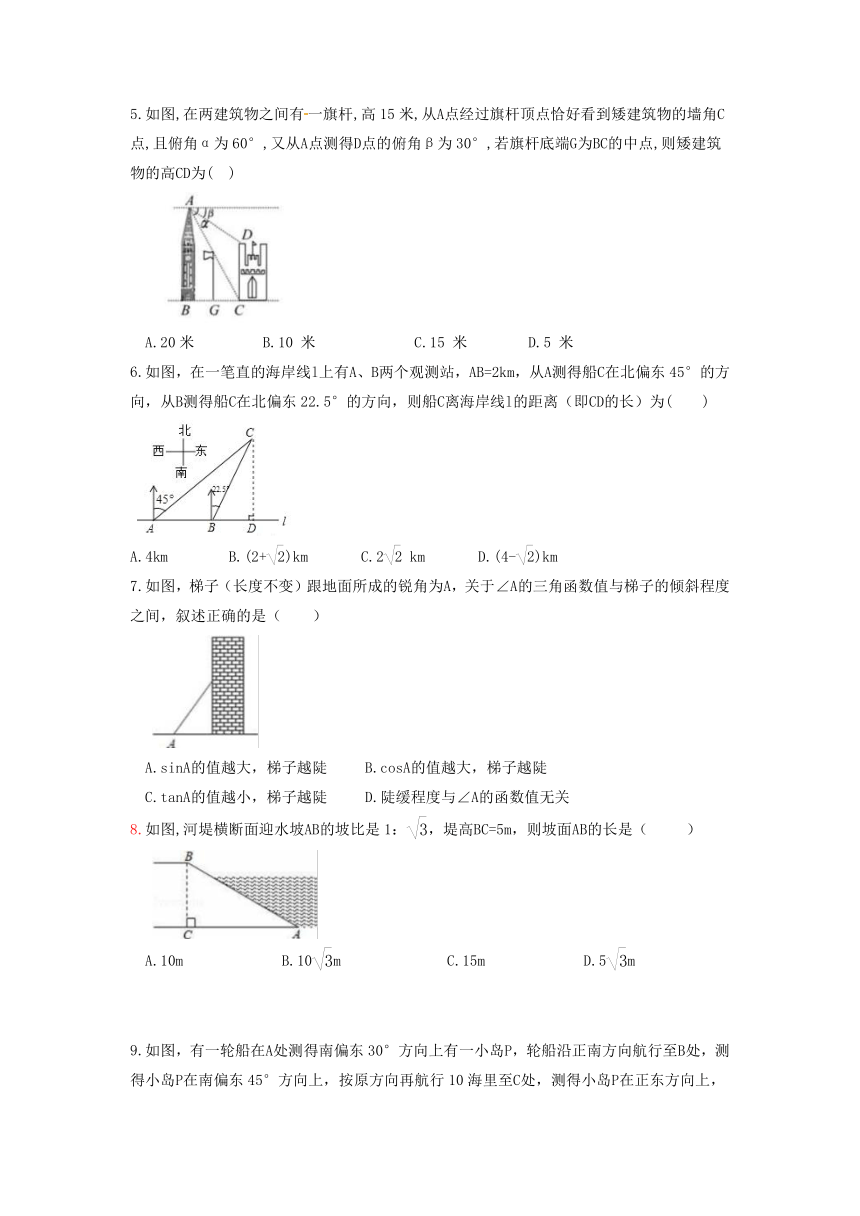
如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底端G为BC的中点,则矮建筑物的高CD为( )
A.20米 B.10 米 C.15 米 D.5 米
如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km,从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为( )
A.4km B.(2+)km C.2 km D.(4-)km
如图,梯子(长度不变)跟地面所成的锐角为A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是( )
A.sinA的值越大,梯子越陡 B.cosA的值越大,梯子越陡
C.tanA的值越小,梯子越陡 D.陡缓程度与∠A的函数值无关
如图,河堤横断面迎水坡AB的坡比是1:,堤高BC=5m,则坡面AB的长是( )
A.10m B.10m C.15m D.5m
如图,有一轮船在A处测得南偏东30°方向上有一小岛P,轮船沿正南方向航行至B处,测得小岛P在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛P在正东方向上,则A,B之间的距离是( )
A.10海里 B.(10-10)海里 C.10海里 D.(10-10)海里
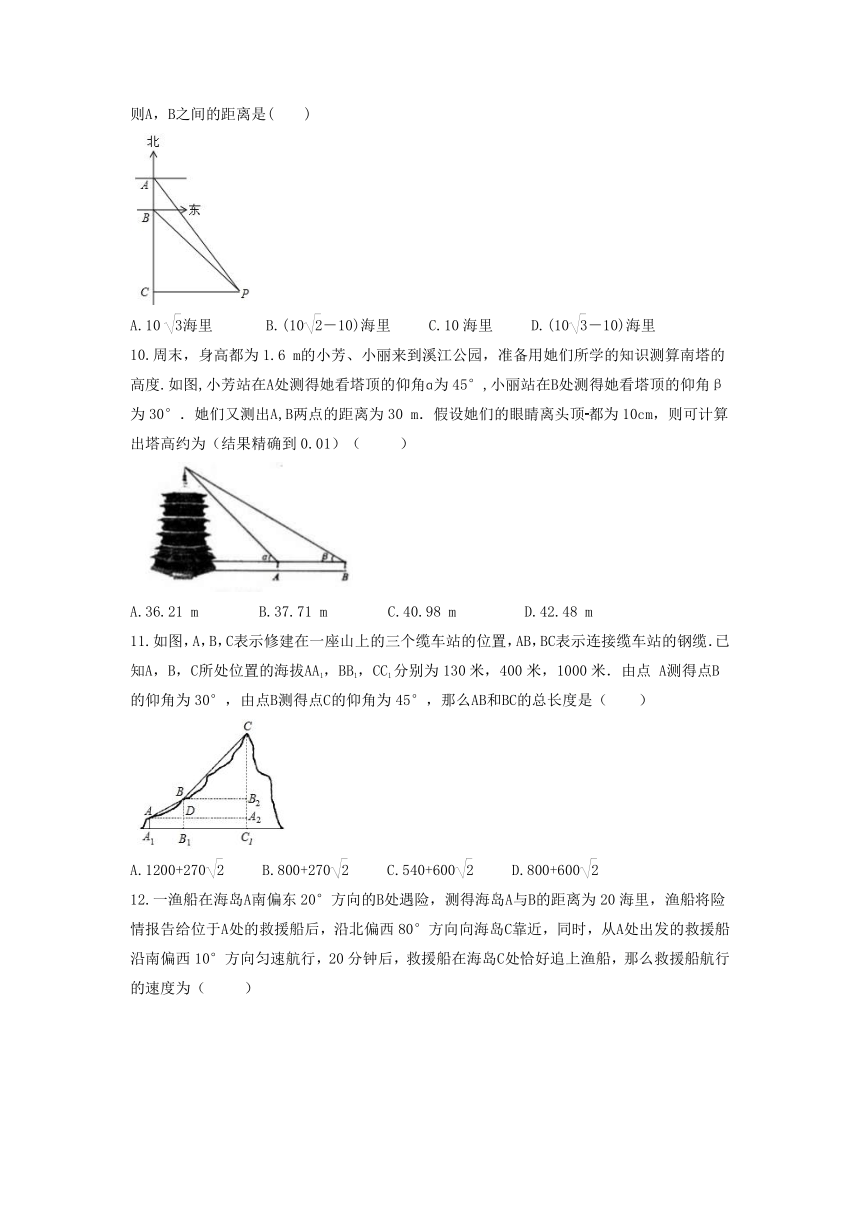
周末,身高都为1.6 m的小芳、小丽来到溪江公园,准备用她们所学的知识测算南塔的高度.如图,小芳站在A处测得她看塔顶的仰角ɑ为45°,小丽站在B处测得她看塔顶的仰角β为30°.她们又测出A,B两点的距离为30 m.假设她们的眼睛离头顶都为10cm,则可计算出塔高约为(结果精确到0.01)( )
A.36.21 m B.37.71 m C.40.98 m D.42.48 m
如图,A,B,C表示修建在一座山上的三个缆车站的位置,AB,BC表示连接缆车站的钢缆.已知A,B,C所处位置的海拔AA1,BB1,CC1分别为130米,400米,1000米.由点 A测得点B的仰角为30°,由点B测得点C的仰角为45°,那么AB和BC的总长度是( )
A.1200+270 B.800+270 C.540+600 D.800+600
一渔船在海岛A南偏东20°方向的B处遇险,测得海岛A与B的距离为20海里,渔船将险情报告给位于A处的救援船后,沿北偏西80°方向向海岛C靠近,同时,从A处出发的救援船沿南偏西10°方向匀速航行,20分钟后,救援船在海岛C处恰好追上渔船,那么救援船航行的速度为( )
A.10海里/小时 B.30海里/小时 C.20海里/小时 D.30海里/小时
二、填空题
如图,一根竖直的木杆在离地面3.1m处折断,木杆顶端落在地面上,且与地面成38°角,
则木杆折断之前高度约为 m.
(参考数据:sin38°≈0.62,cos38°≈0.79,tan38°≈0.78)
如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,那么山高AD为 米(结果保留整数,测角仪忽略不计)
如图,李明在一块平地上测山高,现在B出测得山顶A的仰角为30°,然后再向山脚直行100米到达C处,再测得山顶A的仰角为60°,那么山高AD为 米.
某轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,又继续航行7海里后,在B处测得小岛P的方位是北偏东60°,则此时轮船与小岛P的距离BP=__________海里.
如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为5m,则大树的高度为 m(结果保留根号)
如图,为测量某塔AB的高度,在离塔底部10米处目测其塔顶A,仰角为60°,目高1.5米,则求该塔的高度为 米.(参考数据:≈1.41,≈1.73)
三、解答题
芜湖长江大桥采用低塔斜拉桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2 m,两拉索底端距离AD为20 m,请求出立柱BH的长.(结果精确到0.1 m,≈1.732)
“低碳环保,你我同行”.近几年,各大城市的公共自行车给市民出行带来了极大的方便.图①是公共自行车的实物图,图②是公共自行车的车架示意图,点A、D、C、E在同一条直线上,CD=30cm,DF=20cm,AF=25cm,FD⊥AE于点D,座杆CE=15cm,且∠EAB=75°.
(1)求AD的长;
(2)求点E到AB的距离.(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)
如图,已知长江路西段与黄河路的夹角为150°,长江路东段与淮河路的夹角为135°,黄河路全长AC=20km,从A地道B地必须先走黄河路经C点后再走淮河路才能到达,城市道路改造后,直接打通长江路(即修建AB路段).
问:打通长江路后从A地道B地可少走多少路程?(参考数据:≈1.4,≈1.7)
如图,放置在水平桌面上的台灯的灯臂AB长为40cm,灯罩BC长为30cm,底座厚度为2cm,灯臂与底座构成的∠BAD=60°, 使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少cm?
如图所示,某公路检测中心在一事故多发地带安装了一个测速仪,检测点设在距离公路10 m的A处,测得一辆汽车从B处行驶到C处所用的时间为0.9秒.已知∠B=30°,∠C=45°.
(1)求B,C之间的距离;(保留根号)
(2)如果此地限速为80 km/h,那么这辆汽车是否超速?请说明理由.
(参考数据:≈1.7,≈1,4)
某挖掘机的底座高AB=0.8米,动臂BC=1.2米,CD=1.5米,BC与CD的固定夹角∠BCD=140°.初始位置如图1,斗杆顶点D与铲斗顶点E所在直线DE垂直地面AM于点E,测得∠CDE=70°(示意图2).工作时如图3,动臂BC会绕点B转动,当点A,B,C在同一直线时,斗杆顶点D升至最高点(示意图4).
(1)求挖掘机在初始位置时动臂BC与AB的夹角∠ABC的度数.
(2)问斗杆顶点D的最高点比初始位置高了多少米(精确到0.1米)?
(参考数据:sin50°≈0.77,cos50°≈0.64,sin70°≈0.94,cos70°≈0.34,≈1.73)
参考答案
1.C.
2.B
3.C
4.B.
5.A
6.B
7.A
8.A
9.D
10.D
11.C
12.D
13.答案为:8.1.
14.答案为:137.
15.答案为:50.
16.答案为:7
17.答案为:(5+5).
18.答案为:18.8米
19.解:设DH=x米,∵∠CDH=60°,∠H=90°,
在Rt△CHD中,∴CH=DH·tan 60°=x,
∴BH=BC+CH=2+x,
∵∠A=30°,
同理,∴AH=BH=2+3x,
∵AH=AD+DH,
∴2+3x=20+x,解得:x=10-,
∴BH=2+(10-)=10-1≈16.3(m).
答:立柱BH的长约为16.3 m.
20.解:
21.解:如图所示:过点C作CD⊥AB于点D,
在Rt△ACD中,∠CAD=30°,AC=20km,则CD=10km,AD=10km,
在Rt△BCD中,∠CBD=45°,CD=10km,故BD=10km,BC=10km,
则AC+BC﹣AB=20+10﹣10﹣10≈7(km),
答:打通长江路后从A地道B地可少走7km的路程.
22.解:过点B作BM⊥CE于点M,BF⊥DA于点F,如图所示.
在Rt△BCM中,BC=30cm,∠CBM=30°,
∴CM=BC sin∠CBM=15cm.
在Rt△ABF中,AB=40cm,∠BAD=60°,
∴BF=AB sin∠BAD=20cm.
∵∠ADC=∠BMD=∠BFD=90°,
∴四边形BFDM为矩形,
∴MD=BF,
∴CE=CM+MD+DE=CM+BF+ED=15+20+2=20+17(cm).
答:此时灯罩顶端C到桌面的高度CE是(20+17)cm.
23.解:(1)过点A作AD⊥BC于点D,则AD=10 m.
∵在Rt△ACD中,∠C=45°,
∴CD=AD=10 m.
在Rt△ABD中,tanB=,
∵∠B=30°,
∴=.
∴BD=10 m.
∴BC=BD+DC=(10+10)m.
答:B,C之间的距离是(10+10)m.
(2)这辆汽车超速,理由如下:
由(1)知BC=(10+10)m≈27 m.
∴汽车速度为=30(m/s)=108 km/h.
∵108>80,
∴这辆汽车超速.
24.解:(1)过点C作CG⊥AM于点G,如图1,
∵AB⊥AM,DE⊥AM,∴AB∥CG∥DE,∴∠DCG=180°﹣∠CDE=110°,
∴BCG=∠BCD﹣∠GCD=30°,∴∠ABC=180°﹣∠BCG=150°;
(2)过点C作CP⊥DE于点P,过点B作BQ⊥DE于点Q,交CG于点N,如图2,
在Rt△CPD中,DP=CP×cos70°≈0.51(米),
在Rt△BCN中,CN=BC×cos30°≈1.04(米),
所以,DE=DP+PQ+QE=DP+CN+AB=2.35(米),
如图3,过点D作DH⊥AM于点H,过点C作CK⊥DH于点K,
在Rt△CKD中,DK=CD×cos50°≈1.16(米),所以,DH=DK+KH=3.16(米),
所以,DH﹣DE=0.8(米),
所以,斗杆顶点D的最高点比初始位置高了0.8米.
《解直角三角形的应用》同步练习卷
一、选择题
如图,在地面上的点A处测得树顶B的仰角为α度,AC=7 m,则树高BC为(用含α的代数式表示)( )
A.7sinα B.7cosα C.7tanα D.
如图,为了测量河两岸A、B两点的距离,在与AB垂直的方向点C处测得AC=a,
∠ACB=α,那么AB=( )
A.asinα B.atanα C.acosα D.
如图,A,B两点在河的两岸,要测量这两点之间的距离,测量者在与A同侧的河岸边选定一点C,测出AC=a米,∠BAC=90°,∠ACB=40°,则AB等于( )
A.asin40°米 B.acos40°米 C.atan40°米 D.米
某简易房示意图如图所示,它是一个轴对称图形,则坡屋顶上弦杆AB的长为( )
A.米 B.米 C.米 D.米
如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底端G为BC的中点,则矮建筑物的高CD为( )
A.20米 B.10 米 C.15 米 D.5 米
如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km,从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为( )
A.4km B.(2+)km C.2 km D.(4-)km
如图,梯子(长度不变)跟地面所成的锐角为A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是( )
A.sinA的值越大,梯子越陡 B.cosA的值越大,梯子越陡
C.tanA的值越小,梯子越陡 D.陡缓程度与∠A的函数值无关
如图,河堤横断面迎水坡AB的坡比是1:,堤高BC=5m,则坡面AB的长是( )
A.10m B.10m C.15m D.5m
如图,有一轮船在A处测得南偏东30°方向上有一小岛P,轮船沿正南方向航行至B处,测得小岛P在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛P在正东方向上,则A,B之间的距离是( )
A.10海里 B.(10-10)海里 C.10海里 D.(10-10)海里
周末,身高都为1.6 m的小芳、小丽来到溪江公园,准备用她们所学的知识测算南塔的高度.如图,小芳站在A处测得她看塔顶的仰角ɑ为45°,小丽站在B处测得她看塔顶的仰角β为30°.她们又测出A,B两点的距离为30 m.假设她们的眼睛离头顶都为10cm,则可计算出塔高约为(结果精确到0.01)( )
A.36.21 m B.37.71 m C.40.98 m D.42.48 m
如图,A,B,C表示修建在一座山上的三个缆车站的位置,AB,BC表示连接缆车站的钢缆.已知A,B,C所处位置的海拔AA1,BB1,CC1分别为130米,400米,1000米.由点 A测得点B的仰角为30°,由点B测得点C的仰角为45°,那么AB和BC的总长度是( )
A.1200+270 B.800+270 C.540+600 D.800+600
一渔船在海岛A南偏东20°方向的B处遇险,测得海岛A与B的距离为20海里,渔船将险情报告给位于A处的救援船后,沿北偏西80°方向向海岛C靠近,同时,从A处出发的救援船沿南偏西10°方向匀速航行,20分钟后,救援船在海岛C处恰好追上渔船,那么救援船航行的速度为( )
A.10海里/小时 B.30海里/小时 C.20海里/小时 D.30海里/小时
二、填空题
如图,一根竖直的木杆在离地面3.1m处折断,木杆顶端落在地面上,且与地面成38°角,
则木杆折断之前高度约为 m.
(参考数据:sin38°≈0.62,cos38°≈0.79,tan38°≈0.78)
如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,那么山高AD为 米(结果保留整数,测角仪忽略不计)
如图,李明在一块平地上测山高,现在B出测得山顶A的仰角为30°,然后再向山脚直行100米到达C处,再测得山顶A的仰角为60°,那么山高AD为 米.
某轮船由西向东航行,在A处测得小岛P的方位是北偏东75°,又继续航行7海里后,在B处测得小岛P的方位是北偏东60°,则此时轮船与小岛P的距离BP=__________海里.
如图,在建筑平台CD的顶部C处,测得大树AB的顶部A的仰角为45°,测得大树AB的底部B的俯角为30°,已知平台CD的高度为5m,则大树的高度为 m(结果保留根号)
如图,为测量某塔AB的高度,在离塔底部10米处目测其塔顶A,仰角为60°,目高1.5米,则求该塔的高度为 米.(参考数据:≈1.41,≈1.73)
三、解答题
芜湖长江大桥采用低塔斜拉桥型(如甲图),图乙是从图甲引申出的平面图,假设你站在桥上测得拉索AB与水平桥面的夹角是30°,拉索CD与水平桥面的夹角是60°,两拉索顶端的距离BC为2 m,两拉索底端距离AD为20 m,请求出立柱BH的长.(结果精确到0.1 m,≈1.732)
“低碳环保,你我同行”.近几年,各大城市的公共自行车给市民出行带来了极大的方便.图①是公共自行车的实物图,图②是公共自行车的车架示意图,点A、D、C、E在同一条直线上,CD=30cm,DF=20cm,AF=25cm,FD⊥AE于点D,座杆CE=15cm,且∠EAB=75°.
(1)求AD的长;
(2)求点E到AB的距离.(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73)
如图,已知长江路西段与黄河路的夹角为150°,长江路东段与淮河路的夹角为135°,黄河路全长AC=20km,从A地道B地必须先走黄河路经C点后再走淮河路才能到达,城市道路改造后,直接打通长江路(即修建AB路段).
问:打通长江路后从A地道B地可少走多少路程?(参考数据:≈1.4,≈1.7)
如图,放置在水平桌面上的台灯的灯臂AB长为40cm,灯罩BC长为30cm,底座厚度为2cm,灯臂与底座构成的∠BAD=60°, 使用发现,光线最佳时灯罩BC与水平线所成的角为30°,此时灯罩顶端C到桌面的高度CE是多少cm?
如图所示,某公路检测中心在一事故多发地带安装了一个测速仪,检测点设在距离公路10 m的A处,测得一辆汽车从B处行驶到C处所用的时间为0.9秒.已知∠B=30°,∠C=45°.
(1)求B,C之间的距离;(保留根号)
(2)如果此地限速为80 km/h,那么这辆汽车是否超速?请说明理由.
(参考数据:≈1.7,≈1,4)
某挖掘机的底座高AB=0.8米,动臂BC=1.2米,CD=1.5米,BC与CD的固定夹角∠BCD=140°.初始位置如图1,斗杆顶点D与铲斗顶点E所在直线DE垂直地面AM于点E,测得∠CDE=70°(示意图2).工作时如图3,动臂BC会绕点B转动,当点A,B,C在同一直线时,斗杆顶点D升至最高点(示意图4).
(1)求挖掘机在初始位置时动臂BC与AB的夹角∠ABC的度数.
(2)问斗杆顶点D的最高点比初始位置高了多少米(精确到0.1米)?
(参考数据:sin50°≈0.77,cos50°≈0.64,sin70°≈0.94,cos70°≈0.34,≈1.73)
参考答案
1.C.
2.B
3.C
4.B.
5.A
6.B
7.A
8.A
9.D
10.D
11.C
12.D
13.答案为:8.1.
14.答案为:137.
15.答案为:50.
16.答案为:7
17.答案为:(5+5).
18.答案为:18.8米
19.解:设DH=x米,∵∠CDH=60°,∠H=90°,
在Rt△CHD中,∴CH=DH·tan 60°=x,
∴BH=BC+CH=2+x,
∵∠A=30°,
同理,∴AH=BH=2+3x,
∵AH=AD+DH,
∴2+3x=20+x,解得:x=10-,
∴BH=2+(10-)=10-1≈16.3(m).
答:立柱BH的长约为16.3 m.
20.解:
21.解:如图所示:过点C作CD⊥AB于点D,
在Rt△ACD中,∠CAD=30°,AC=20km,则CD=10km,AD=10km,
在Rt△BCD中,∠CBD=45°,CD=10km,故BD=10km,BC=10km,
则AC+BC﹣AB=20+10﹣10﹣10≈7(km),
答:打通长江路后从A地道B地可少走7km的路程.
22.解:过点B作BM⊥CE于点M,BF⊥DA于点F,如图所示.
在Rt△BCM中,BC=30cm,∠CBM=30°,
∴CM=BC sin∠CBM=15cm.
在Rt△ABF中,AB=40cm,∠BAD=60°,
∴BF=AB sin∠BAD=20cm.
∵∠ADC=∠BMD=∠BFD=90°,
∴四边形BFDM为矩形,
∴MD=BF,
∴CE=CM+MD+DE=CM+BF+ED=15+20+2=20+17(cm).
答:此时灯罩顶端C到桌面的高度CE是(20+17)cm.
23.解:(1)过点A作AD⊥BC于点D,则AD=10 m.
∵在Rt△ACD中,∠C=45°,
∴CD=AD=10 m.
在Rt△ABD中,tanB=,
∵∠B=30°,
∴=.
∴BD=10 m.
∴BC=BD+DC=(10+10)m.
答:B,C之间的距离是(10+10)m.
(2)这辆汽车超速,理由如下:
由(1)知BC=(10+10)m≈27 m.
∴汽车速度为=30(m/s)=108 km/h.
∵108>80,
∴这辆汽车超速.
24.解:(1)过点C作CG⊥AM于点G,如图1,
∵AB⊥AM,DE⊥AM,∴AB∥CG∥DE,∴∠DCG=180°﹣∠CDE=110°,
∴BCG=∠BCD﹣∠GCD=30°,∴∠ABC=180°﹣∠BCG=150°;
(2)过点C作CP⊥DE于点P,过点B作BQ⊥DE于点Q,交CG于点N,如图2,
在Rt△CPD中,DP=CP×cos70°≈0.51(米),
在Rt△BCN中,CN=BC×cos30°≈1.04(米),
所以,DE=DP+PQ+QE=DP+CN+AB=2.35(米),
如图3,过点D作DH⊥AM于点H,过点C作CK⊥DH于点K,
在Rt△CKD中,DK=CD×cos50°≈1.16(米),所以,DH=DK+KH=3.16(米),
所以,DH﹣DE=0.8(米),
所以,斗杆顶点D的最高点比初始位置高了0.8米.
