2021-2022鲁教版数学九年级上册第二章直角三角形的边角关系 单元练习(word版含解析)
文档属性
| 名称 | 2021-2022鲁教版数学九年级上册第二章直角三角形的边角关系 单元练习(word版含解析) | 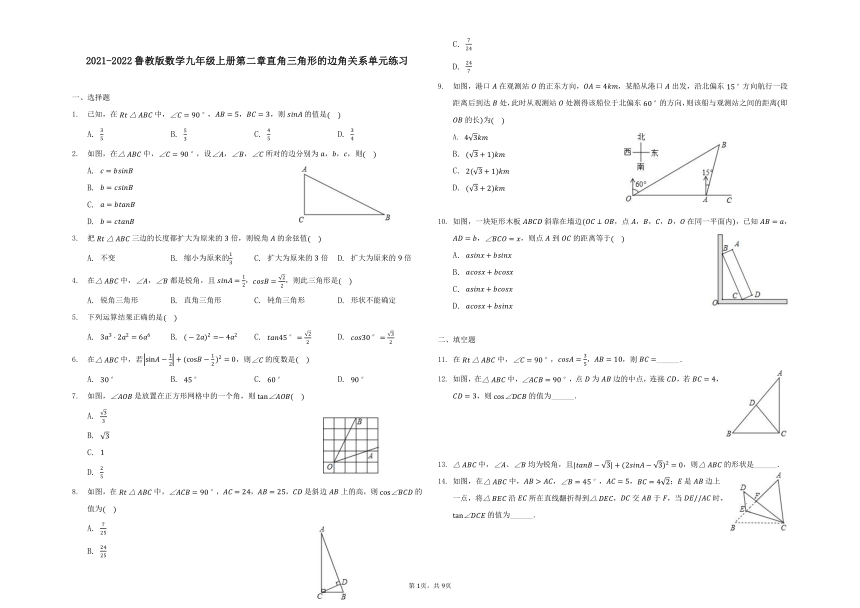 | |
| 格式 | zip | ||
| 文件大小 | 177.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-04 09:55:52 | ||
图片预览



文档简介
2021-2022鲁教版数学九年级上册第二章直角三角形的边角关系单元练习
一、选择题
已知,在中,,,,则的值是
A. B. C. D.
如图,在中,,设,,所对的边分别为,,,则
A.
B.
C.
D.
把三边的长度都扩大为原来的倍,则锐角的余弦值
A. 不变 B. 缩小为原来的 C. 扩大为原来的倍 D. 扩大为原来的倍
在中,,都是锐角,且,,则此三角形是
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 形状不能确定
下列运算结果正确的是
A. B. C. D.
在中,若,则的度数是
A. B. C. D.
如图,是放置在正方形网格中的一个角,则
A.
B.
C.
D.
如图,在中,,,,是斜边上的高,则的值为
A.
B.
C.
D.
如图,港口在观测站的正东方向,,某船从港口出发,沿北偏东方向航行一段距离后到达处,此时从观测站处测得该船位于北偏东的方向,则该船与观测站之间的距离即的长为
B.
C.
D.
如图,一块矩形木板斜靠在墙边,点,,,,在同一平面内,已知,,,则点到的距离等于
A.
B.
C.
D.
二、填空题
在中,,,,则______.
如图,在中,,点为边的中点,连接,若,,则的值为______.
中,、均为锐角,且,则的形状是______.
如图,在中,,,,;是边上一点,将沿所在直线翻折得到,交于,当时,的值为______.
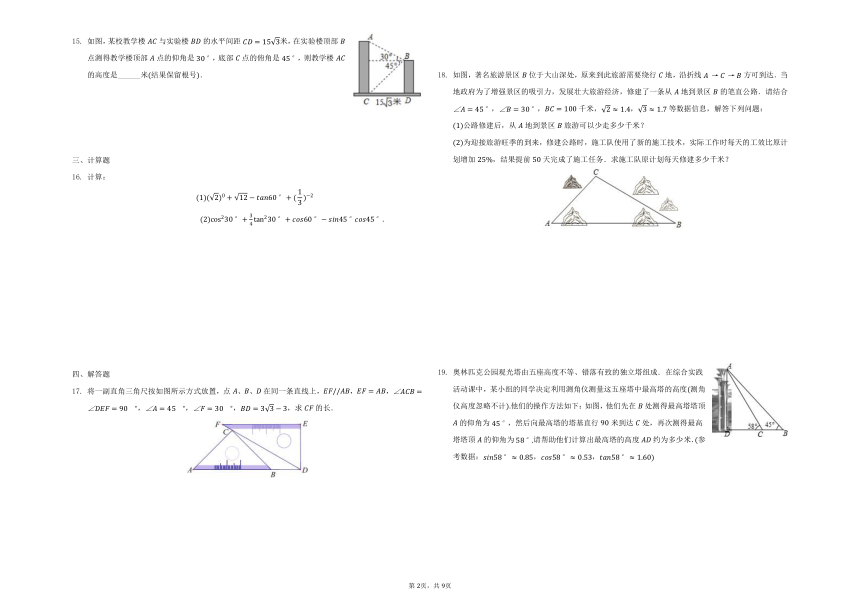
如图,某校教学楼与实验楼的水平间距米,在实验楼顶部点测得教学楼顶部点的仰角是,底部点的俯角是,则教学楼的高度是______米结果保留根号.
三、计算题
计算:
.
四、解答题
将一副直角三角尺按如图所示方式放置,点、、在同一条直线上,,,,,,,求的长.
如图,著名旅游景区位于大山深处,原来到此旅游需要绕行地,沿折线方可到达.当地政府为了增强景区的吸引力,发展壮大旅游经济,修建了一条从地到景区的笔直公路.请结合,,千米,,等数据信息,解答下列问题:
公路修建后,从地到景区旅游可以少走多少千米?
为迎接旅游旺季的到来,修建公路时,施工队使用了新的施工技术,实际工作时每天的工效比原计划增加,结果提前天完成了施工任务.求施工队原计划每天修建多少千米?
奥林匹克公园观光塔由五座高度不等、错落有致的独立塔组成.在综合实践活动课中,某小组的同学决定利用测角仪测量这五座塔中最高塔的高度测角仪高度忽略不计他们的操作方法如下:如图,他们先在处测得最高塔塔顶的仰角为,然后向最高塔的塔基直行米到达处,再次测得最高塔塔顶的仰角为请帮助他们计算出最高塔的高度约为多少米.参考数据:,,
为了维护国家主权和海洋权力,海监部门对我国领海实现了常态化巡航管理,如图,正在执行巡航任务的海监船以每小时海里的速度向正东方航行,在处测得灯塔在北偏东方向上,继续航行小时到达处,此时测得灯塔在北偏东方向上.
求的度数;
已知在灯塔的周围海里内有暗礁,问海监船继续向正东方向航行是否安全?
如图,某拦河坝横截面原设计方案为梯形,其中,,为了提高拦河坝的安全性,现将坝顶宽度水平缩短,坝底宽度水平增加,使,请你计算这个拦河大坝的高度.参考数据:,,
答案和解析
1.【答案】
【解析】解:,
故选:.
根据正弦函数是对边比斜边,可得答案.
本题考查了锐角三角函数,利用正弦函数是对边比斜边是解题关键.
2.【答案】
【解析】
【分析】
本题主要考查了锐角三角函数的定义,属于基础题.
根据锐角三角函数的定义,进行判断,就可以解决问题.
【解答】
解:中,,、、所对的边分别为、、,
,即,故A选项不成立,选项成立;
,即,故C选项不成立,选项不成立.
故选:.
3.【答案】
【解析】
【分析】
本题考查的是相似三角形的判定和性质、锐角三角函数的定义,掌握相似三角形的对应角相等是解题的关键.
根据相似三角形的性质解答.
【解答】
解:三边的长度都扩大为原来的倍,
则所得的三角形与原三角形相似,
锐角的大小不变,
锐角的余弦值不变,
故选:.
4.【答案】
【解析】解:,,
,,
.
故选:.
根据特殊角的三角函数值即可求得和的度数,然后求得的度数,据此即可判断.
本题考查了特殊角的三角函数值,解决此类题目的关键是熟记特殊角的三角函数值.
5.【答案】
【解析】解:、原式,故本选项错误;
B、原式,故本选项错误;
C、原式,故本选项错误;
D、原式,故本选项正确.
故选:.
根据同底数幂的乘法、幂的乘方与积的乘方、特殊角的三角函数值进行计算.
考查了同底数幂的乘法、幂的乘方与积的乘方、特殊角的三角函数值,属于基础计算题.
6.【答案】
【解析】
【分析】
本题主要考查了非负实数的性质,特殊角的锐角三角函数值,三角形内角和定理,首先由两非负数的和为,则它们同时为,求出和的值,从而得到和的度数,再由三角形内角和为进行求解即可.
【解答】
解:,
,,
,,
、是的内角,
,,
,,
,
故选D.
7.【答案】
【解析】解:如图,连接.
观察图象可知是等腰直角三角形,
,,
,
故选:.
利用等腰直角三角形的性质即可解问题即可.
本题考查解直角三角形,等腰直角三角形的性质等知识,解题的关键是学会利用数形结合的思想思考问题,属于中考常考题型.
8.【答案】
【解析】解:在中,,,,
,
是斜边上的高,,
,
,
,
,
故选:.
根据题意和题目中的数据,利用勾股定理可以求得的长,然后根据等积法可以求得的长,从而可以求得的值.
本题考查解直角三角形、勾股定理,解答本题的关键是明确题意,利用锐角三角函数解答.
9.【答案】
【解析】解:如图,过点作于.
在中,,,,
,,
在中,,,
,
,
即该船与观测站之间的距离即的长为.
故选:.
过点作于先解,得出,,再由是等腰直角三角形,得出,于是得到结论.
本题考查了解直角三角形的应用方向角问题,难度适中,作出辅助线构造直角三角形是解题的关键.
10.【答案】
【解析】
【分析】
本题考查解直角三角形的应用坡度角问题、矩形的性质,解答本题的关键是明确题意,利用数形结合的思想解答.
根据题意,作出合适的辅助线,然后利用锐角三角函数即可表示出点到的距离,本题得以解决.
【解答】
解:作于点,作于点,
四边形是矩形,
,
,,
,
,
,,
,
故选D.
11.【答案】
【解析】解:由题可知:,
则.
故答案为:.
直接利用锐角三角三角函数关系得出的长,再利用勾股定理得出答案.
此题主要考查了锐角三角三角函数关系,正确得出的长是解题关键.
12.【答案】
【解析】解:过点作,垂足为,
,,
,
又点为边的中点,
,
在中,,
故答案为:.
过点作,由平行线平分线段定理可得是的中点,再根据三角函数的意义,可求出答案.
本题考查直角三角形的边角关系,理解直角三角形的边角关系是得出正确答案的前提,作高构造直角三角形是常用的方法.
13.【答案】等边三角形
【解析】解:,
,.
,;,.
的形状是等边三角形.
先根据非负数的性质及特殊教的三角函数值求出,的度数,再根据三角形的内角和定理求出的度数,最后根据三个内角关系判断出其形状.
本题考查了:特殊角的三角函数值;非负数的性质;三角形的内角和定理.
14.【答案】
【解析】解:如图,作于,于,
,,
,
,
,
,
将沿所在直线翻折得到,且,
,,
,
,
,
,
,
,
.
故答案为:.
作于,于,因为,,所以,因为,所以,,由题意,可得,,
所以,即,可得,,在中,利用锐角三角函数定义即可得出的值.
本题考查图形的翻折,平行线的性质,锐角三角函数的定义和解直角三角形的知识.解题的关键是熟练掌握图形翻折的性质.
15.【答案】
【解析】
【分析】
本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形.
首先分析图形:根据题意构造直角三角形.本题涉及到两个直角三角形、,进而可解即可求出答案.
【解答】
解:过点作于点,
在中,,,
可得米.
在中,,,
可得米.
故教学楼的高度是米.
答:教学楼的高度是米.
16.【答案】解:原式;
原式.
【解析】原式第一项利用零指数幂法则计算,第二项化为最简二次根式,第三项利用特殊角的三角函数值计算,最后一项利用负整数指数幂法则计算即可得到结果;
原式利用特殊角的三角函数值计算即可得到结果.
此题考查了实数的运算,熟练掌握运算法则是解本题的关键.
17.【答案】解:作于点,
在等腰中,,
,
在中,
设 ,,,
,
解得:,
即
,.
在中,,,,
.
【解析】本题主要考查了解直角三角形在三角形中的运用,关键是熟练掌握各锐角三角函数的定义先添加辅助线高线,根据等腰直角三角形的性质可得,根据平行线可得的度数,在直角三角形中,根据正切函数得出,进一步可得的长度,在直角三角形中,根据余弦函数可得,最后根据线段的和差关系可得结果.
18.【答案】解:过点作的垂线,垂足为,
在直角中,,,千米,
千米,
千米,
在直角中,千米,
千米,
千米,
从地到景区旅游可以少走:
千米.
答:从地到景区旅游可以少走千米;
设施工队原计划每天修建千米,
依题意有,,
解得,
经检验是原分式方程的解.
答:施工队原计划每天修建约千米.
【解析】本题考查解直角三角形的应用、分式方程的应用,解答本题的关键是明确题意,利用数形结合的思想解答.
过点作的垂线,垂足为,在直角中,解直角三角形求出的长度和的长度,在直角中,解直角三角形求出的长度和的长度,再求出的长度,进而求出从地到景区旅游可以少走多少千米;
本题先由题意找出等量关系即原计划的工作时间实际的工作时间,然后列出方程可求出结果,最后检验并作答.
19.【答案】解:,,
,
,
设,则,
,
,
解得:,
米,
答:最高塔的高度约为米.
【解析】根据已知条件求出,设,得出,再根据,求出的值,即可得出的值.
本题考查了解直角三角形的应用,要求学生能借助仰角构造直角三角形并解直角三角形,注意方程思想的运用.
20.【答案】解:由题意得,,,
,
由可知,
海里
过点作于点,在中,
海里
海监船继续向正东方向航行是安全的.
【解析】在中,求出、的度数即可解决问题;
作于求出的值即可判定;
本题考查的是解直角三角形的应用方向角问题,正确根据题意画出图形、准确标注方向角、熟练掌握锐角三角函数的概念是解题的关键.
21.【答案】解:过点作于点,过点作垂直于点,
设拦河大坝的高度为,
在和中,
,,
,
,
,,,
,
解得:,
答:拦河大坝的高度为.
【解析】过点作于点,过点作垂直于点,设拦河大坝的高度为,在和中分别求出和的长度,然后根据已知,,,列方程求出的值即可.
本题考查了解直角三角形的应用,关键是根据坡度和坡角构造直角三角形,在直角三角形中利用三角函数求解,难度一般.
第2页,共2页
第1页,共1页
一、选择题
已知,在中,,,,则的值是
A. B. C. D.
如图,在中,,设,,所对的边分别为,,,则
A.
B.
C.
D.
把三边的长度都扩大为原来的倍,则锐角的余弦值
A. 不变 B. 缩小为原来的 C. 扩大为原来的倍 D. 扩大为原来的倍
在中,,都是锐角,且,,则此三角形是
A. 锐角三角形 B. 直角三角形 C. 钝角三角形 D. 形状不能确定
下列运算结果正确的是
A. B. C. D.
在中,若,则的度数是
A. B. C. D.
如图,是放置在正方形网格中的一个角,则
A.
B.
C.
D.
如图,在中,,,,是斜边上的高,则的值为
A.
B.
C.
D.
如图,港口在观测站的正东方向,,某船从港口出发,沿北偏东方向航行一段距离后到达处,此时从观测站处测得该船位于北偏东的方向,则该船与观测站之间的距离即的长为
B.
C.
D.
如图,一块矩形木板斜靠在墙边,点,,,,在同一平面内,已知,,,则点到的距离等于
A.
B.
C.
D.
二、填空题
在中,,,,则______.
如图,在中,,点为边的中点,连接,若,,则的值为______.
中,、均为锐角,且,则的形状是______.
如图,在中,,,,;是边上一点,将沿所在直线翻折得到,交于,当时,的值为______.
如图,某校教学楼与实验楼的水平间距米,在实验楼顶部点测得教学楼顶部点的仰角是,底部点的俯角是,则教学楼的高度是______米结果保留根号.
三、计算题
计算:
.
四、解答题
将一副直角三角尺按如图所示方式放置,点、、在同一条直线上,,,,,,,求的长.
如图,著名旅游景区位于大山深处,原来到此旅游需要绕行地,沿折线方可到达.当地政府为了增强景区的吸引力,发展壮大旅游经济,修建了一条从地到景区的笔直公路.请结合,,千米,,等数据信息,解答下列问题:
公路修建后,从地到景区旅游可以少走多少千米?
为迎接旅游旺季的到来,修建公路时,施工队使用了新的施工技术,实际工作时每天的工效比原计划增加,结果提前天完成了施工任务.求施工队原计划每天修建多少千米?
奥林匹克公园观光塔由五座高度不等、错落有致的独立塔组成.在综合实践活动课中,某小组的同学决定利用测角仪测量这五座塔中最高塔的高度测角仪高度忽略不计他们的操作方法如下:如图,他们先在处测得最高塔塔顶的仰角为,然后向最高塔的塔基直行米到达处,再次测得最高塔塔顶的仰角为请帮助他们计算出最高塔的高度约为多少米.参考数据:,,
为了维护国家主权和海洋权力,海监部门对我国领海实现了常态化巡航管理,如图,正在执行巡航任务的海监船以每小时海里的速度向正东方航行,在处测得灯塔在北偏东方向上,继续航行小时到达处,此时测得灯塔在北偏东方向上.
求的度数;
已知在灯塔的周围海里内有暗礁,问海监船继续向正东方向航行是否安全?
如图,某拦河坝横截面原设计方案为梯形,其中,,为了提高拦河坝的安全性,现将坝顶宽度水平缩短,坝底宽度水平增加,使,请你计算这个拦河大坝的高度.参考数据:,,
答案和解析
1.【答案】
【解析】解:,
故选:.
根据正弦函数是对边比斜边,可得答案.
本题考查了锐角三角函数,利用正弦函数是对边比斜边是解题关键.
2.【答案】
【解析】
【分析】
本题主要考查了锐角三角函数的定义,属于基础题.
根据锐角三角函数的定义,进行判断,就可以解决问题.
【解答】
解:中,,、、所对的边分别为、、,
,即,故A选项不成立,选项成立;
,即,故C选项不成立,选项不成立.
故选:.
3.【答案】
【解析】
【分析】
本题考查的是相似三角形的判定和性质、锐角三角函数的定义,掌握相似三角形的对应角相等是解题的关键.
根据相似三角形的性质解答.
【解答】
解:三边的长度都扩大为原来的倍,
则所得的三角形与原三角形相似,
锐角的大小不变,
锐角的余弦值不变,
故选:.
4.【答案】
【解析】解:,,
,,
.
故选:.
根据特殊角的三角函数值即可求得和的度数,然后求得的度数,据此即可判断.
本题考查了特殊角的三角函数值,解决此类题目的关键是熟记特殊角的三角函数值.
5.【答案】
【解析】解:、原式,故本选项错误;
B、原式,故本选项错误;
C、原式,故本选项错误;
D、原式,故本选项正确.
故选:.
根据同底数幂的乘法、幂的乘方与积的乘方、特殊角的三角函数值进行计算.
考查了同底数幂的乘法、幂的乘方与积的乘方、特殊角的三角函数值,属于基础计算题.
6.【答案】
【解析】
【分析】
本题主要考查了非负实数的性质,特殊角的锐角三角函数值,三角形内角和定理,首先由两非负数的和为,则它们同时为,求出和的值,从而得到和的度数,再由三角形内角和为进行求解即可.
【解答】
解:,
,,
,,
、是的内角,
,,
,,
,
故选D.
7.【答案】
【解析】解:如图,连接.
观察图象可知是等腰直角三角形,
,,
,
故选:.
利用等腰直角三角形的性质即可解问题即可.
本题考查解直角三角形,等腰直角三角形的性质等知识,解题的关键是学会利用数形结合的思想思考问题,属于中考常考题型.
8.【答案】
【解析】解:在中,,,,
,
是斜边上的高,,
,
,
,
,
故选:.
根据题意和题目中的数据,利用勾股定理可以求得的长,然后根据等积法可以求得的长,从而可以求得的值.
本题考查解直角三角形、勾股定理,解答本题的关键是明确题意,利用锐角三角函数解答.
9.【答案】
【解析】解:如图,过点作于.
在中,,,,
,,
在中,,,
,
,
即该船与观测站之间的距离即的长为.
故选:.
过点作于先解,得出,,再由是等腰直角三角形,得出,于是得到结论.
本题考查了解直角三角形的应用方向角问题,难度适中,作出辅助线构造直角三角形是解题的关键.
10.【答案】
【解析】
【分析】
本题考查解直角三角形的应用坡度角问题、矩形的性质,解答本题的关键是明确题意,利用数形结合的思想解答.
根据题意,作出合适的辅助线,然后利用锐角三角函数即可表示出点到的距离,本题得以解决.
【解答】
解:作于点,作于点,
四边形是矩形,
,
,,
,
,
,,
,
故选D.
11.【答案】
【解析】解:由题可知:,
则.
故答案为:.
直接利用锐角三角三角函数关系得出的长,再利用勾股定理得出答案.
此题主要考查了锐角三角三角函数关系,正确得出的长是解题关键.
12.【答案】
【解析】解:过点作,垂足为,
,,
,
又点为边的中点,
,
在中,,
故答案为:.
过点作,由平行线平分线段定理可得是的中点,再根据三角函数的意义,可求出答案.
本题考查直角三角形的边角关系,理解直角三角形的边角关系是得出正确答案的前提,作高构造直角三角形是常用的方法.
13.【答案】等边三角形
【解析】解:,
,.
,;,.
的形状是等边三角形.
先根据非负数的性质及特殊教的三角函数值求出,的度数,再根据三角形的内角和定理求出的度数,最后根据三个内角关系判断出其形状.
本题考查了:特殊角的三角函数值;非负数的性质;三角形的内角和定理.
14.【答案】
【解析】解:如图,作于,于,
,,
,
,
,
,
将沿所在直线翻折得到,且,
,,
,
,
,
,
,
,
.
故答案为:.
作于,于,因为,,所以,因为,所以,,由题意,可得,,
所以,即,可得,,在中,利用锐角三角函数定义即可得出的值.
本题考查图形的翻折,平行线的性质,锐角三角函数的定义和解直角三角形的知识.解题的关键是熟练掌握图形翻折的性质.
15.【答案】
【解析】
【分析】
本题考查俯角、仰角的定义,要求学生能借助俯角、仰角构造直角三角形并结合图形利用三角函数解直角三角形.
首先分析图形:根据题意构造直角三角形.本题涉及到两个直角三角形、,进而可解即可求出答案.
【解答】
解:过点作于点,
在中,,,
可得米.
在中,,,
可得米.
故教学楼的高度是米.
答:教学楼的高度是米.
16.【答案】解:原式;
原式.
【解析】原式第一项利用零指数幂法则计算,第二项化为最简二次根式,第三项利用特殊角的三角函数值计算,最后一项利用负整数指数幂法则计算即可得到结果;
原式利用特殊角的三角函数值计算即可得到结果.
此题考查了实数的运算,熟练掌握运算法则是解本题的关键.
17.【答案】解:作于点,
在等腰中,,
,
在中,
设 ,,,
,
解得:,
即
,.
在中,,,,
.
【解析】本题主要考查了解直角三角形在三角形中的运用,关键是熟练掌握各锐角三角函数的定义先添加辅助线高线,根据等腰直角三角形的性质可得,根据平行线可得的度数,在直角三角形中,根据正切函数得出,进一步可得的长度,在直角三角形中,根据余弦函数可得,最后根据线段的和差关系可得结果.
18.【答案】解:过点作的垂线,垂足为,
在直角中,,,千米,
千米,
千米,
在直角中,千米,
千米,
千米,
从地到景区旅游可以少走:
千米.
答:从地到景区旅游可以少走千米;
设施工队原计划每天修建千米,
依题意有,,
解得,
经检验是原分式方程的解.
答:施工队原计划每天修建约千米.
【解析】本题考查解直角三角形的应用、分式方程的应用,解答本题的关键是明确题意,利用数形结合的思想解答.
过点作的垂线,垂足为,在直角中,解直角三角形求出的长度和的长度,在直角中,解直角三角形求出的长度和的长度,再求出的长度,进而求出从地到景区旅游可以少走多少千米;
本题先由题意找出等量关系即原计划的工作时间实际的工作时间,然后列出方程可求出结果,最后检验并作答.
19.【答案】解:,,
,
,
设,则,
,
,
解得:,
米,
答:最高塔的高度约为米.
【解析】根据已知条件求出,设,得出,再根据,求出的值,即可得出的值.
本题考查了解直角三角形的应用,要求学生能借助仰角构造直角三角形并解直角三角形,注意方程思想的运用.
20.【答案】解:由题意得,,,
,
由可知,
海里
过点作于点,在中,
海里
海监船继续向正东方向航行是安全的.
【解析】在中,求出、的度数即可解决问题;
作于求出的值即可判定;
本题考查的是解直角三角形的应用方向角问题,正确根据题意画出图形、准确标注方向角、熟练掌握锐角三角函数的概念是解题的关键.
21.【答案】解:过点作于点,过点作垂直于点,
设拦河大坝的高度为,
在和中,
,,
,
,
,,,
,
解得:,
答:拦河大坝的高度为.
【解析】过点作于点,过点作垂直于点,设拦河大坝的高度为,在和中分别求出和的长度,然后根据已知,,,列方程求出的值即可.
本题考查了解直角三角形的应用,关键是根据坡度和坡角构造直角三角形,在直角三角形中利用三角函数求解,难度一般.
第2页,共2页
第1页,共1页
