沪科版数学八年级上册 12.2 一次函数复习 课件(共20张PPT)
文档属性
| 名称 | 沪科版数学八年级上册 12.2 一次函数复习 课件(共20张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 567.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-04 08:24:14 | ||
图片预览







文档简介
(共20张PPT)
反比例函数及其应用
一、反比例函数解析式的三种形式
1.y=___(k≠0,k为常数).
2.y=k___(k≠0,k为常数).
3.xy=__(k≠0,k为常数).
x-1
k
二、反比例函数的图象与性质
1.反比例函数y= (k为常数,k≠0)的图象是_______,且关于_____对称.
双曲线
原点
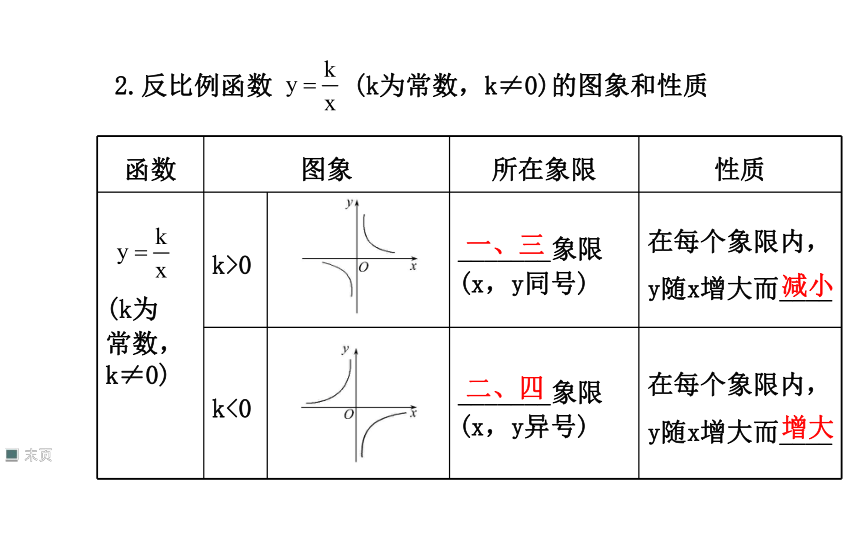
2.反比例函数 (k为常数,k≠0)的图象和性质
函数 图象 所在象限 性质
(k为 常数, k≠0) k>0 _______象限 (x,y同号) 在每个象限内,y随x增大而____
k<0 _______象限 (x,y异号) 在每个象限内,y随x增大而____
一、三
减小
二、四
增大
【思维诊断】(打“√”或“×”)
1.若 是反比例函数,则a的取值为±1. ( )
2.若反比例函数 的图象过点(5,-1),则实数k的值是-5.
( )
3.反比例函数 中,y随着x的增大而减小. ( )
4.若点A(1,y1),B(2,y2)都在反比例函数 (k>0)的图象
上,则y1,y2的大小关系为y1×
√
×
×
热点一 反比例函数的图象和性质
【例1】(1)下列关于反比例函数 的三
个结论:①它的图象经过点(7,3);②它的图象在每一个象限
内,y随x的增大而减小;③它的图象在二、四象限内.其中正
确的是 .
(2)若函数 的图象在同一象限
内,y随x的增大而增大,则m的值可以是 .(写出一个
即可)
【真题专练】
1.若反比例函数 的图象位于第二、四象限,则k的取值可能是 ( )
A.0 B.2 C.3 D.4
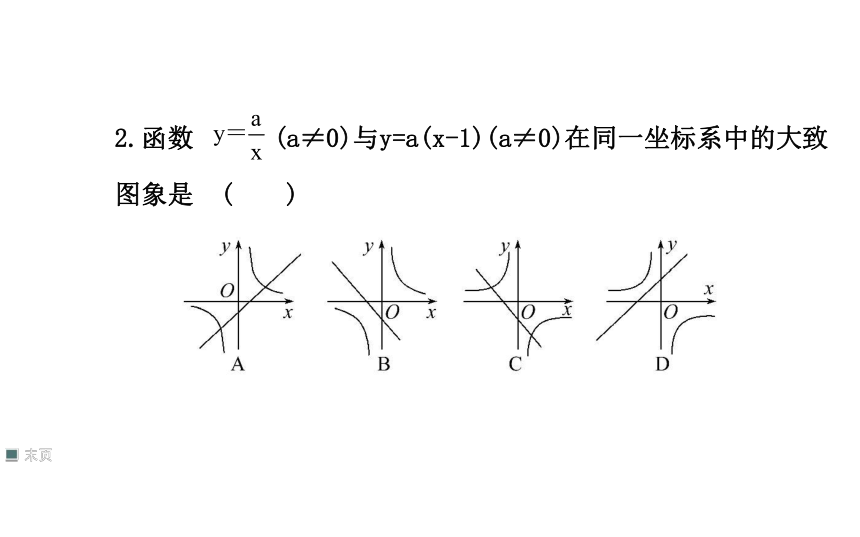
2.函数 (a≠0)与y=a(x-1)(a≠0)在同一坐标系中的大致图象是 ( )
3.关于反比例函数 的图象,下列说法正确的是 ( )
A.图象经过点(1,1)
B.两个分支分布在第二、四象限
C.两个分支关于x轴成轴对称
D.当x<0时,y随x的增大而减小
热点考向二 确定反比例函数的解析式
【例2】反比例函数 的图象经过点(-2,3),则k的值为 ( )
A.6 B.-6 C. D.
【思路点拨】将点的坐标代入反比例函数的解析式求解.
【自主解答】选C.将点的坐标(-2,3)代入得 ,
解得 .
2.已知反比例函数 ,当x=2时,y=3.
(1)求m的值.
(2)当3≤x≤6时,求函数值y的取值范围.
【解析】(1)把x=2,y=3代入 得到5-m=6,所以m=-1.
(2)当x=3时,由 得y=2;
x=6时,由 得y=1.
当3≤x≤6时,y随x的增大而减小,
所以函数值的范围是1≤y≤2.
热点考向三 反比例函数的应用
【例3】在一个可以改变体积的密闭容器内
装有一定质量的某种气体,当改变容器的
体积时,气体的密度也会随之改变.密度
ρ(单位:kg/m3)与体积V(单位:m3)
满足函数关系式 (k为常数,k≠0),其图象如图所示,则k的值为 ( )
A.9 B.-9 C.4 D.-4
【思路点拨】分析函数图象可知过点A(6,1.5),把(6,1.5)代入 即可求得k的值.
【自主解答】选A.把V=6,ρ=1.5代入 得,k=9.
【真题专练】
1.如图,边长为1的正方形ABCD中,点E在CB延长线上,连接ED交AB于点F,AF=x(0.2≤x≤0.8),EC=y.则在下面函数图象中,大致能反映y与x之间函数关系的是
( )
【解析】选C.由题意知,△ADF∽△BEF,所以 ,
即 所以 ,y与x之间的函数
关系是反比例函数,所以选C.
热点考向 与反比例函数有关的综合题
【例】 如图,在直角坐标系xOy中,
直线y=mx与双曲线 相交于
A(-1,a)、B两点,BC⊥x轴,垂足为C,
△AOC的面积是1.
(1)求m,n的值;
(2)求直线AC的解析式.
【自主解答】(1)∵直线y=mx与双曲线 相交于A(-1,a),B两点,
∴A,B两点关于原点O对称.
∵A(-1,a),
∴B点横坐标为1,而BC⊥x轴,
∴C(1,0).
∵△AOC的面积为1,∴A(-1,2).
将A(-1,2)代入y=mx, ,
可得m=-2,n=-2.
(2)设直线AC的解析式为:y=kx+b(k≠0).
∵y=kx+b经过点A(-1,2),C(1,0),
∴ 解得k=-1,b=1.
∴直线AC的解析式为y=-x+1.
(10分)(2016 安徽)如图,一次函数y=kx+b的图象分别与反比例函数y= 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
(1)求函数y=kx+b和y= 的表达式;
(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.
反比例函数及其应用
一、反比例函数解析式的三种形式
1.y=___(k≠0,k为常数).
2.y=k___(k≠0,k为常数).
3.xy=__(k≠0,k为常数).
x-1
k
二、反比例函数的图象与性质
1.反比例函数y= (k为常数,k≠0)的图象是_______,且关于_____对称.
双曲线
原点
2.反比例函数 (k为常数,k≠0)的图象和性质
函数 图象 所在象限 性质
(k为 常数, k≠0) k>0 _______象限 (x,y同号) 在每个象限内,y随x增大而____
k<0 _______象限 (x,y异号) 在每个象限内,y随x增大而____
一、三
减小
二、四
增大
【思维诊断】(打“√”或“×”)
1.若 是反比例函数,则a的取值为±1. ( )
2.若反比例函数 的图象过点(5,-1),则实数k的值是-5.
( )
3.反比例函数 中,y随着x的增大而减小. ( )
4.若点A(1,y1),B(2,y2)都在反比例函数 (k>0)的图象
上,则y1,y2的大小关系为y1
√
×
×
热点一 反比例函数的图象和性质
【例1】(1)下列关于反比例函数 的三
个结论:①它的图象经过点(7,3);②它的图象在每一个象限
内,y随x的增大而减小;③它的图象在二、四象限内.其中正
确的是 .
(2)若函数 的图象在同一象限
内,y随x的增大而增大,则m的值可以是 .(写出一个
即可)
【真题专练】
1.若反比例函数 的图象位于第二、四象限,则k的取值可能是 ( )
A.0 B.2 C.3 D.4
2.函数 (a≠0)与y=a(x-1)(a≠0)在同一坐标系中的大致图象是 ( )
3.关于反比例函数 的图象,下列说法正确的是 ( )
A.图象经过点(1,1)
B.两个分支分布在第二、四象限
C.两个分支关于x轴成轴对称
D.当x<0时,y随x的增大而减小
热点考向二 确定反比例函数的解析式
【例2】反比例函数 的图象经过点(-2,3),则k的值为 ( )
A.6 B.-6 C. D.
【思路点拨】将点的坐标代入反比例函数的解析式求解.
【自主解答】选C.将点的坐标(-2,3)代入得 ,
解得 .
2.已知反比例函数 ,当x=2时,y=3.
(1)求m的值.
(2)当3≤x≤6时,求函数值y的取值范围.
【解析】(1)把x=2,y=3代入 得到5-m=6,所以m=-1.
(2)当x=3时,由 得y=2;
x=6时,由 得y=1.
当3≤x≤6时,y随x的增大而减小,
所以函数值的范围是1≤y≤2.
热点考向三 反比例函数的应用
【例3】在一个可以改变体积的密闭容器内
装有一定质量的某种气体,当改变容器的
体积时,气体的密度也会随之改变.密度
ρ(单位:kg/m3)与体积V(单位:m3)
满足函数关系式 (k为常数,k≠0),其图象如图所示,则k的值为 ( )
A.9 B.-9 C.4 D.-4
【思路点拨】分析函数图象可知过点A(6,1.5),把(6,1.5)代入 即可求得k的值.
【自主解答】选A.把V=6,ρ=1.5代入 得,k=9.
【真题专练】
1.如图,边长为1的正方形ABCD中,点E在CB延长线上,连接ED交AB于点F,AF=x(0.2≤x≤0.8),EC=y.则在下面函数图象中,大致能反映y与x之间函数关系的是
( )
【解析】选C.由题意知,△ADF∽△BEF,所以 ,
即 所以 ,y与x之间的函数
关系是反比例函数,所以选C.
热点考向 与反比例函数有关的综合题
【例】 如图,在直角坐标系xOy中,
直线y=mx与双曲线 相交于
A(-1,a)、B两点,BC⊥x轴,垂足为C,
△AOC的面积是1.
(1)求m,n的值;
(2)求直线AC的解析式.
【自主解答】(1)∵直线y=mx与双曲线 相交于A(-1,a),B两点,
∴A,B两点关于原点O对称.
∵A(-1,a),
∴B点横坐标为1,而BC⊥x轴,
∴C(1,0).
∵△AOC的面积为1,∴A(-1,2).
将A(-1,2)代入y=mx, ,
可得m=-2,n=-2.
(2)设直线AC的解析式为:y=kx+b(k≠0).
∵y=kx+b经过点A(-1,2),C(1,0),
∴ 解得k=-1,b=1.
∴直线AC的解析式为y=-x+1.
(10分)(2016 安徽)如图,一次函数y=kx+b的图象分别与反比例函数y= 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
(1)求函数y=kx+b和y= 的表达式;
(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.
