黑龙江省齐齐哈尔市2021-2022学年高一上学期期末考试数学试卷(Word版含答案)
文档属性
| 名称 | 黑龙江省齐齐哈尔市2021-2022学年高一上学期期末考试数学试卷(Word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 598.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-03 00:00:00 | ||
图片预览




文档简介
齐齐哈尔市2021-2022学年高一上学期期末考试
数学试卷
本试卷分第Ⅰ 卷 (选择题) 和第 II 卷(非选择题)两部分.
全卷共 150 分, 考试时间 120 分钟. 考生作答时, 将答案答在答题卡上, 在本试卷上答 题无效. 考试结束后, 将本试卷和答题卡一并交回.
注意事项:
答题前, 考生先将自己的姓名、准考证号码填写清楚, 将条形码准确粘贴在条形码 区域内.
选择题必须使用 铅笔填涂; 非选择题必须使用 毫米黑色字迹的签字筁书写, 字体工整、笔迹清楚.
请按照题号顺序在各题目的答题区域内作答, 超出答题区域书写的答案无效; 在草 稿纸、试题卷上答题无效.
作图可先使用 铅笔填涂; 非选择题必须用黑色字迹的签字笔描黑.
保持卡面清洁, 不要折叠、不要弄破、弄皱, 不准使用涂改液、修正带、刮纸刀.
第I 卷
一、单选题(本大题共 8 个小题, 每小题 5 分, 共 40 分. 在每小题给出的四个选项中, 只有一项是符合题目要求的)
已知集合 , 则
A.
B.
C.
D.
一个半径为 4 的扇形, 其弧长为 1 , 则该扇形的圆心角的弧度数为
A.
B.
C.
D. 2
已知 , 且 为第四象限角, 则
A.
B.
C.
D.
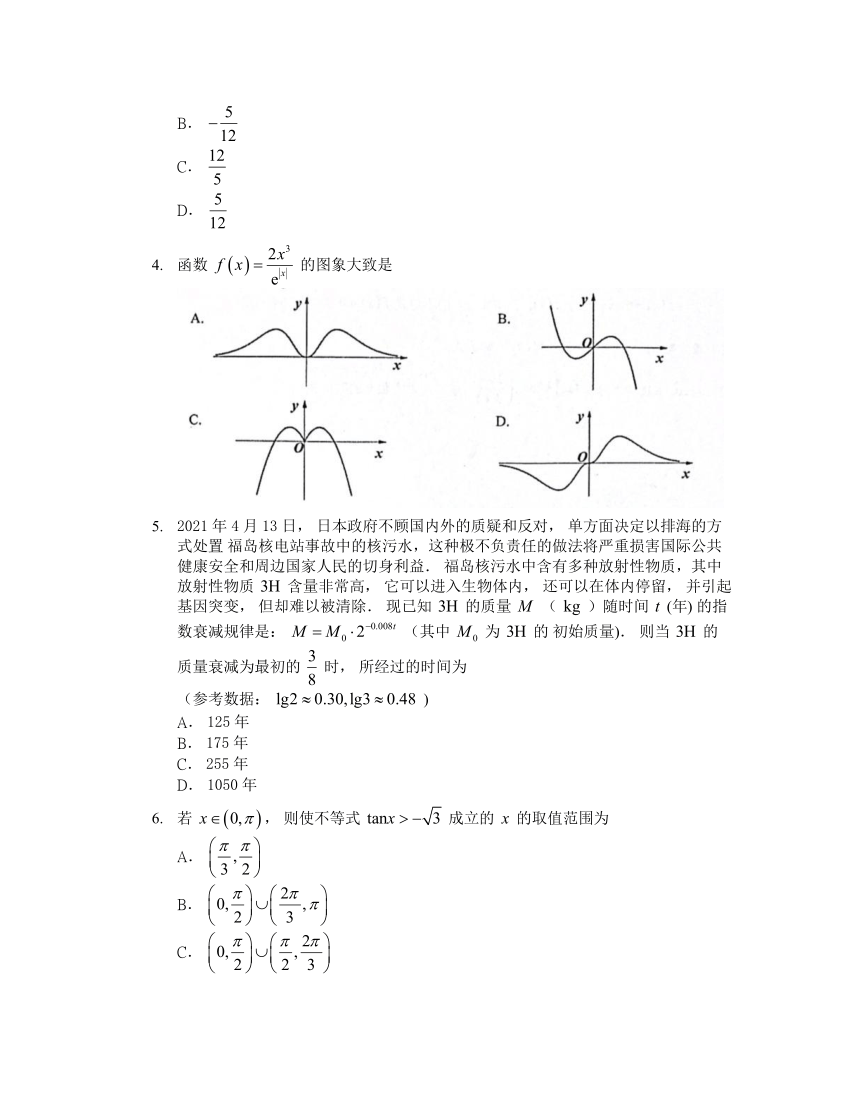
函数 的图象大致是
2021 年 4 月 13 日, 日本政府不顾国内外的质疑和反对, 单方面决定以排海的方式处置 福岛核电站事故中的核污水,这种极不负责任的做法将严重损害国际公共健康安全和周边国家人民的切身利益. 福岛核污水中含有多种放射性物质,其中放射性物质 含量非常高, 它可以进入生物体内, 还可以在体内停留, 并引起基因突变, 但却难以被清除. 现已知 的质量 ( )随时间 (年) 的指数衰减规律是: (其中 为 的 初始质量). 则当 的质量衰减为最初的 时, 所经过的时间为
(参考数据: )
A. 125 年
B. 175 年
C. 255 年
D. 1050 年
若 , 则使不等式 成立的 的取值范围为
A.
B.
C.
D.
字有“数学王子”称号的德国数学家高斯, 是近代数学奠基者之一. 被称为“高斯函 数",其中 表示不超过 的最大整数,例如 设 为函数 的零点, 则
A. 3
B. 4
C. 5
D. 6
已知定义在 上的奇函数 满足 , 当 时, , 则
A.
B. 2
C.
D.
二、多选题(本大题共 4 小题,每小题 5 分,共 20 分. 在每小题给出的选项中, 有 多项符合题目要求, 全部选对的得 5 分, 部分选对的得 2 分, 有选错的得 0 分)
已知下列等式的左、石两边都有意义, 则能够恒成立的足
A.
B.
C.
D.
下列命题正确的是
A. 是 的充分不必要条件
B. 是 的充分条件
C.
D.
已知函数 , 则下列说法正确的是
A. 的 最小正周期为
B. 为偶函数
C. 的值域为
D. 恒成立
已知 , 则下列不等关系一定正确的是
A.
B.
C.
D.
第II卷
三、填空题 (本大题共 4 小题, 烸小题 5 分, 共 20 分)
若函数 是幂函数, 且是偶函数, 则 ________.
已知角 的终边经过点 , 则 ________.
以下各式的值都等于同一个常数 , 请你观察, 写出这个常数 的值________ ;根据你的理解, 写出一个符合这些式子规律的等式________________________.
(注:第一空 2 分, 第二空 3 分)
函数 , 若 恒成立, 则实数 的取值范围是________.
四、解答题 (本大题共 6 小题, 共 70 分. 解答应写出文字说明、证明过程或演算步骤)
(10 分) 化简求值:
(1) ;
(2) 已知 , 求 的值.
(12 分) 设全集 , 集合 , 非空集合 , 其中 .
(1)当 吋, 求 .
(2) 若“ "是“ ”的________ 条件, 求 的取值范围(请在“①充分; ②必要”两 个条件中选一个条件填入横线后作答).
(12 分) 已知函数 .
(1) 若 , 求 的值;
(2) 求 的单调递璔区间;
(3) 当 时, 求 的最大值和最小值.
(12 分) 在市场调研的基础上, 某工厂今年 1月、2月、3月份分别生产了 A 产品 100 件、 120 件、 130 件.为了估测该产品以后各月所需的生产量, 甲、乙两人均以这三个月的生 产量为依据进行了模拟试验。甲选择的数学模型是: , 乙选择的数学模型 是: , (其中 为 产品的生产量, 为月份数, 都是 常数), 现已知 4 月份和 5 月份实际需要生产 产品 136 件和 138 件. 据此, 你认为谁选 择的模型更符合实际 (请写出选择的结果和理由)
(12 分) 设函数 . 用 表示 中的较大 者, 记为 .已知关于 的不等式 的解集为 .
(1) 求实数 的值, 并写出 的解析式:
(2)若 , 使得 成立, 求实数 的取值范围.
(12 分) 已知函数 的图 关于原点对称.
(1) 求实数 的值;
(2) (1)判断 在区间 上的单调性(只写出结论即可);
(2)若关于 的方程 在区间 上有两个不同的解, 求实 数 的取值范围.
数学试卷
本试卷分第Ⅰ 卷 (选择题) 和第 II 卷(非选择题)两部分.
全卷共 150 分, 考试时间 120 分钟. 考生作答时, 将答案答在答题卡上, 在本试卷上答 题无效. 考试结束后, 将本试卷和答题卡一并交回.
注意事项:
答题前, 考生先将自己的姓名、准考证号码填写清楚, 将条形码准确粘贴在条形码 区域内.
选择题必须使用 铅笔填涂; 非选择题必须使用 毫米黑色字迹的签字筁书写, 字体工整、笔迹清楚.
请按照题号顺序在各题目的答题区域内作答, 超出答题区域书写的答案无效; 在草 稿纸、试题卷上答题无效.
作图可先使用 铅笔填涂; 非选择题必须用黑色字迹的签字笔描黑.
保持卡面清洁, 不要折叠、不要弄破、弄皱, 不准使用涂改液、修正带、刮纸刀.
第I 卷
一、单选题(本大题共 8 个小题, 每小题 5 分, 共 40 分. 在每小题给出的四个选项中, 只有一项是符合题目要求的)
已知集合 , 则
A.
B.
C.
D.
一个半径为 4 的扇形, 其弧长为 1 , 则该扇形的圆心角的弧度数为
A.
B.
C.
D. 2
已知 , 且 为第四象限角, 则
A.
B.
C.
D.
函数 的图象大致是
2021 年 4 月 13 日, 日本政府不顾国内外的质疑和反对, 单方面决定以排海的方式处置 福岛核电站事故中的核污水,这种极不负责任的做法将严重损害国际公共健康安全和周边国家人民的切身利益. 福岛核污水中含有多种放射性物质,其中放射性物质 含量非常高, 它可以进入生物体内, 还可以在体内停留, 并引起基因突变, 但却难以被清除. 现已知 的质量 ( )随时间 (年) 的指数衰减规律是: (其中 为 的 初始质量). 则当 的质量衰减为最初的 时, 所经过的时间为
(参考数据: )
A. 125 年
B. 175 年
C. 255 年
D. 1050 年
若 , 则使不等式 成立的 的取值范围为
A.
B.
C.
D.
字有“数学王子”称号的德国数学家高斯, 是近代数学奠基者之一. 被称为“高斯函 数",其中 表示不超过 的最大整数,例如 设 为函数 的零点, 则
A. 3
B. 4
C. 5
D. 6
已知定义在 上的奇函数 满足 , 当 时, , 则
A.
B. 2
C.
D.
二、多选题(本大题共 4 小题,每小题 5 分,共 20 分. 在每小题给出的选项中, 有 多项符合题目要求, 全部选对的得 5 分, 部分选对的得 2 分, 有选错的得 0 分)
已知下列等式的左、石两边都有意义, 则能够恒成立的足
A.
B.
C.
D.
下列命题正确的是
A. 是 的充分不必要条件
B. 是 的充分条件
C.
D.
已知函数 , 则下列说法正确的是
A. 的 最小正周期为
B. 为偶函数
C. 的值域为
D. 恒成立
已知 , 则下列不等关系一定正确的是
A.
B.
C.
D.
第II卷
三、填空题 (本大题共 4 小题, 烸小题 5 分, 共 20 分)
若函数 是幂函数, 且是偶函数, 则 ________.
已知角 的终边经过点 , 则 ________.
以下各式的值都等于同一个常数 , 请你观察, 写出这个常数 的值________ ;根据你的理解, 写出一个符合这些式子规律的等式________________________.
(注:第一空 2 分, 第二空 3 分)
函数 , 若 恒成立, 则实数 的取值范围是________.
四、解答题 (本大题共 6 小题, 共 70 分. 解答应写出文字说明、证明过程或演算步骤)
(10 分) 化简求值:
(1) ;
(2) 已知 , 求 的值.
(12 分) 设全集 , 集合 , 非空集合 , 其中 .
(1)当 吋, 求 .
(2) 若“ "是“ ”的________ 条件, 求 的取值范围(请在“①充分; ②必要”两 个条件中选一个条件填入横线后作答).
(12 分) 已知函数 .
(1) 若 , 求 的值;
(2) 求 的单调递璔区间;
(3) 当 时, 求 的最大值和最小值.
(12 分) 在市场调研的基础上, 某工厂今年 1月、2月、3月份分别生产了 A 产品 100 件、 120 件、 130 件.为了估测该产品以后各月所需的生产量, 甲、乙两人均以这三个月的生 产量为依据进行了模拟试验。甲选择的数学模型是: , 乙选择的数学模型 是: , (其中 为 产品的生产量, 为月份数, 都是 常数), 现已知 4 月份和 5 月份实际需要生产 产品 136 件和 138 件. 据此, 你认为谁选 择的模型更符合实际 (请写出选择的结果和理由)
(12 分) 设函数 . 用 表示 中的较大 者, 记为 .已知关于 的不等式 的解集为 .
(1) 求实数 的值, 并写出 的解析式:
(2)若 , 使得 成立, 求实数 的取值范围.
(12 分) 已知函数 的图 关于原点对称.
(1) 求实数 的值;
(2) (1)判断 在区间 上的单调性(只写出结论即可);
(2)若关于 的方程 在区间 上有两个不同的解, 求实 数 的取值范围.
同课章节目录
