人教版八年级数学上册导学课件:第十五章分式章末小结(共35张PPT)
文档属性
| 名称 | 人教版八年级数学上册导学课件:第十五章分式章末小结(共35张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-04 00:00:00 | ||
图片预览











文档简介
(共35张PPT)
第十五章 章末小结
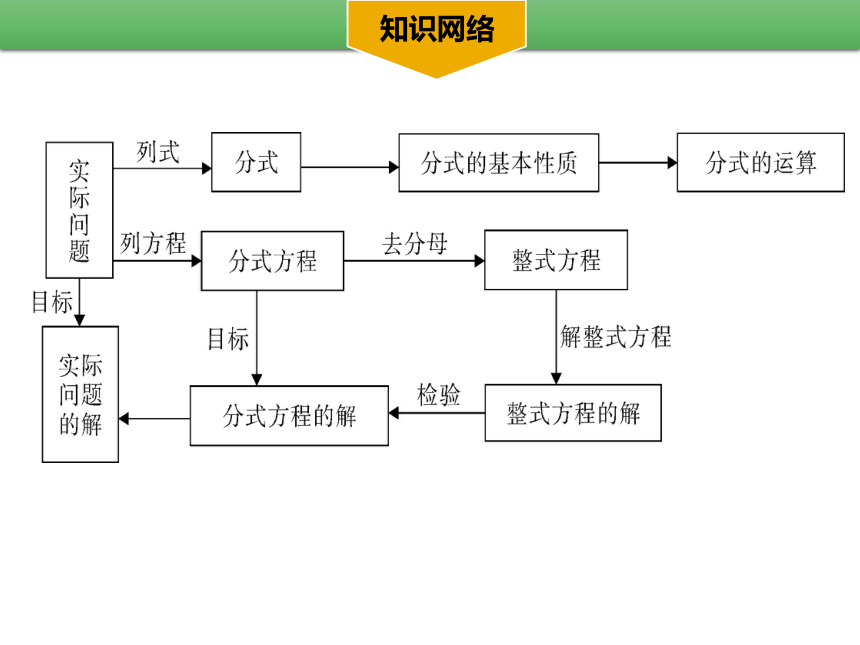
知识网络
专题解读
【解析】根据分式为0的条件得x2-4=0且x-2≠0,解得:x=-2.
专题一:分式的基本概念
专题解读
【答案】C
【点拔】题考查了分式的值为零的条件.
若分式的值为零,需同时具备两个条件:
(1)分子为0;
(2)分母不为0.这两个条件缺一不可.
专题解读
A
B
对点训练一
专题解读
D
B
专题解读
【解析】先对括号中两项通分化成同分母分式后进行减法运算,同时利用除法法则变形,约分得到最简结果,求出不等式组的解集,找出解集中的整数解确定出x的值,代入计算即可求出值.
专题二:分式的有关计算
专题解读
【答案】解:原式
x+4>0
解不等式组 ,得-4<x<-1.
1-2x>3
其整数解为-3,-2.
当x=-3时,原式=4;
当x=-2时,原式无意义.
专题解读
【点拔】此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键
专题解读
5.先化简,再求值:
其中a满足a2+a=6.
对点训练二
专题解读
专题解读
7.先化简,再求值: ,
其中x从0,1,2,3四个数中适当选取.
专题解读
8.
专题解读
【例3】水源村在今年退耕还林活动中,计划植树200亩,全村在完成植树40亩后,某环保组织加入村民植树活动,并且该环保组织植树的速度是全村植树速度的1.5倍,整个植树过程共用了13天完成.
(1)全村每天植树多少亩?
(2)如果全村植树每天需2000元工钱,环保组织是义务植树,因此实际工钱比计划节约多少元?
专题三:分式方程的解法及应用
专题解读
【解析】根据整个植树过程共用了13天完成,以及环保组织植树的速度是全村植树速度的1.5倍表示出两者的植树天数得出等式求出即可.
【答案】解:(1)设全村每天植树x亩,根据题意得
,解得x=8.
经检验x=8是原方程的解,
答:全村每天植树8亩.
专题解读
【点拔】此题主要考查了分式方程的应用,根据植树的天数得出等式是解题关键.
(2)根据题意得:原计划全村植树天数是 =25(天),故可以节省工钱(25-13)×2000=24 000(元).答:如果全村植树每天需2000元工钱,环保组织是义务植树,实际工钱比计划节约24 000元.
专题解读
9.解方程: = .
3
x
2
x-1
方程的两边同乘x(x-1),得3x-3=2x,解得x=3. 检验:把x=3代入x(x-1)=6≠0.
∴原方程的解为:x=3.
对点训练三
专题解读
去分母,得x+2(x-2)=x+2,
解得x=3,经检验x=3是原方程的解,所以原方程的解是x=3.
10.
专题解读
11.当x为何值时,分式 的值比分式
的值大3
3-x
2-x
1
x-2
根据题意得: - =3,方程两边同乘以2-x,得:3-x+1=3(2-x),解得x=1.检验:当x=1时,2-x=1≠0,即x=1是原方程的解,即当x=1时,分式 的值比分式 的值大3.
3-x
2-x
1
x-2
3-x
2-x
1
x-2
专题解读
12.某内陆城市为了落实国家“一带一路”战略,促进经济发展,增强对外贸易的竞争力,把距离港口420km的普通公路升级成了同等长度的高速公路,结果汽车行驶的平均速度比原来提高了50%,行驶时间缩短了2h,求汽车原来的平均速度.
设汽车原来的平均速度是x km/h,根据题意得:
- =2,解得:x=70.经检验:x
=70是原方程的解.答:汽车原来的平均速度70km/h.
420
x
420
(1+50%)
专题解读
13.我市某学校开展“远足行动,磨砺意志,保护森林,爱鸟护鸟”为主题的远足活动.已知学校与某岛相距24千米,远足服务人员骑自行车,学生步行,服务人员骑自行车的平均速度是学生步行平均速度的2.5倍,服务人员与学生同时从学校出发,到达某君山岛时,服务人员所花时间比学生少用了3.6小时,求学生步行的平均速度是多少千米/小时.
专题解读
设学生步行的平均速度是每小时x千米.服务人员骑自行车的平均速度是每小时2.5x千米,
根据题意: - =3.6,解得:x=4,
经检验,x=4是所列方程的解,且符合题意.答:学生步行的平均速度是每小时4千米.
24
x
24 2.5x
专题解读
14.几个小伙伴打算去音乐厅观看演出,他们准备用360元钱购买门票.下面是两个小伙伴的对话:
根据对话的内容,请你求出小伙伴们的人数.
专题解读
解:设票价为x元,由题意得, =
+2,解得:x=60,经检验,x=60是原分式方程的解.则小伙伴的人数为:
+2=8. 答:小伙伴们的人数为8人.
360-72
0.6x
360
x
360
x
专题解读
15.一项工程,甲、乙两公司合作,12天可以完成,共需付工费100 800元,如果甲、乙两公司单独完成此项工程,乙公司所用时间是甲公司的1.5倍,乙公司每天的施工费比甲公司每天的施工费少1 600元.
(1)甲、乙公司单独完成此项工程,各需多少天?
(2)若让一个公司单独完成这项工程,哪个公司施工费较少?
专题解读
(1)设甲公司单独完成此项工程需x天,则乙公司单独完成此项工程需1.5x天.根据题意,得
或 解得x=20,经检验知x=20是方程的解. ∴1.5x=30.答略.
(2)设甲公司每天的施工费为y元,则乙公司每天的施工费为(y-1 600)元,根据题意得12(y+y-1 600)=100 800,解得y=5 000,甲公司单独完成此项工程所需的施工费:20×5 000=100 000(元);
乙公司单独完成此项工程所需的施工费:30×(5 000-1 600)=102 000(元);故甲公司的施工费较少.
专题解读
16.湛茂高速铁路湛江段正在建设中,甲、乙两个工程队计划参与一项工程建设,甲队单独施工30天完成该项工程的 ,这时乙队加入,两队还需同时施工15天,才能完成该项工程.
(1)若乙队单独施工,需要多少天才能完成该项工程?
(2)若甲队参与该项工程施工的时间不超过36天,则乙队至少施工多少天才能完成该项工程?
专题解读
(1)设乙队单独施工,需要x天才能完成该项工程,∵甲队单独施工30天完成该项工程的 ,∴甲队单独施工30÷ =90天完成该项工程,根据题意可得: +15 =1,解得:x=30,检验得:x=30是原方程的根,答:乙队单独施工,需要30天才能完成该项工程;
1
3
1
3
1
3
( + )
1
90
1
x
专题解读
(2)设乙队参与施工y天才能完成该项工程,根据题意可得: ×36+ y≥1,解得:y≥18,答:乙队至少施工18天才能完成该项工程.
1
90
1
30
专题解读
17.近年来雾霾天气给人们的生活带来很大影响,空气质量问题倍受人们关注.某单位计划在室内安装空气净化装置,需购进A、B两种设备.每台B种设备价格比每台A种设备价格多0.7万元,花3万元购买A种设备和花7.2万元购买B种设备的数量相同.
(1)求A种、B种设备每台各多少万元?
(2)根据单位实际情况,需购进A、B两种设备共20台,总费用不高于15万元,求A种设备至少要购买多少台?
专题解读
(1)设每台A种设备x万元,则每台B种设备
(x+0.7)万元,根据题意得: = ,
解得:x=0.5. 经检验,x=0.5是原方程的解,∴x+0.7=1.2. 答:每台A种设备0.5万元,每台B种设备1.2万元.
3
x
7.2
x+0.7
专题解读
(2)设购买A种设备m台,则购买B种设备(20-m)台,根据题意得:0.5m+1.2(20-m)≤15,
解得:m≥ .∵m为整数,∴m≥13.答:A种
设备至少要购买13台.
90
7
专题解读
18.某车行经销的A型自行车去年6月份销售总额为1.6万元,今年由于改造升级每辆车售价比去年增加200元,今年6月份与去年同期相比,销售数量相同,销售总额增加25%.
(1)求今年A型车每辆售价多少元?
(2)该车行计划7月份用不超过4.3万元的资金新进一批A型车和B型车共50辆,应如何进货才能使这批车售完后获利最多?
今年A,B两种型号车的进价和售价如下表:
A型车 B型车
进价(元/辆) 800 950
售价(元/辆) 今年售价 1200
专题解读
(1)设今年A型车每辆售价为x元,则去年A型车每辆售价为(x-200)元,根据题意得:
= ,解得:x=1000,经检验,x=1000是原分式方程的解.
答:今年A型车每辆售价为1000元.
1.6
x-200
1.6×(1+25%)
x
专题解读
(2)设购进A型车m辆,则购进B型车(50-m)辆,根据题意得:800m+950(50-m)≤43000,解得:m≥30.销售利润为(100-800)m+(1200-950)(50-m)=-50m+12500,∵-50<0,∴当m=30时,销售利润最多.答:当购进A型车30辆、购进B型车20辆时,才能使这批车售完后获利最多.
第十五章 章末小结
知识网络
专题解读
【解析】根据分式为0的条件得x2-4=0且x-2≠0,解得:x=-2.
专题一:分式的基本概念
专题解读
【答案】C
【点拔】题考查了分式的值为零的条件.
若分式的值为零,需同时具备两个条件:
(1)分子为0;
(2)分母不为0.这两个条件缺一不可.
专题解读
A
B
对点训练一
专题解读
D
B
专题解读
【解析】先对括号中两项通分化成同分母分式后进行减法运算,同时利用除法法则变形,约分得到最简结果,求出不等式组的解集,找出解集中的整数解确定出x的值,代入计算即可求出值.
专题二:分式的有关计算
专题解读
【答案】解:原式
x+4>0
解不等式组 ,得-4<x<-1.
1-2x>3
其整数解为-3,-2.
当x=-3时,原式=4;
当x=-2时,原式无意义.
专题解读
【点拔】此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键
专题解读
5.先化简,再求值:
其中a满足a2+a=6.
对点训练二
专题解读
专题解读
7.先化简,再求值: ,
其中x从0,1,2,3四个数中适当选取.
专题解读
8.
专题解读
【例3】水源村在今年退耕还林活动中,计划植树200亩,全村在完成植树40亩后,某环保组织加入村民植树活动,并且该环保组织植树的速度是全村植树速度的1.5倍,整个植树过程共用了13天完成.
(1)全村每天植树多少亩?
(2)如果全村植树每天需2000元工钱,环保组织是义务植树,因此实际工钱比计划节约多少元?
专题三:分式方程的解法及应用
专题解读
【解析】根据整个植树过程共用了13天完成,以及环保组织植树的速度是全村植树速度的1.5倍表示出两者的植树天数得出等式求出即可.
【答案】解:(1)设全村每天植树x亩,根据题意得
,解得x=8.
经检验x=8是原方程的解,
答:全村每天植树8亩.
专题解读
【点拔】此题主要考查了分式方程的应用,根据植树的天数得出等式是解题关键.
(2)根据题意得:原计划全村植树天数是 =25(天),故可以节省工钱(25-13)×2000=24 000(元).答:如果全村植树每天需2000元工钱,环保组织是义务植树,实际工钱比计划节约24 000元.
专题解读
9.解方程: = .
3
x
2
x-1
方程的两边同乘x(x-1),得3x-3=2x,解得x=3. 检验:把x=3代入x(x-1)=6≠0.
∴原方程的解为:x=3.
对点训练三
专题解读
去分母,得x+2(x-2)=x+2,
解得x=3,经检验x=3是原方程的解,所以原方程的解是x=3.
10.
专题解读
11.当x为何值时,分式 的值比分式
的值大3
3-x
2-x
1
x-2
根据题意得: - =3,方程两边同乘以2-x,得:3-x+1=3(2-x),解得x=1.检验:当x=1时,2-x=1≠0,即x=1是原方程的解,即当x=1时,分式 的值比分式 的值大3.
3-x
2-x
1
x-2
3-x
2-x
1
x-2
专题解读
12.某内陆城市为了落实国家“一带一路”战略,促进经济发展,增强对外贸易的竞争力,把距离港口420km的普通公路升级成了同等长度的高速公路,结果汽车行驶的平均速度比原来提高了50%,行驶时间缩短了2h,求汽车原来的平均速度.
设汽车原来的平均速度是x km/h,根据题意得:
- =2,解得:x=70.经检验:x
=70是原方程的解.答:汽车原来的平均速度70km/h.
420
x
420
(1+50%)
专题解读
13.我市某学校开展“远足行动,磨砺意志,保护森林,爱鸟护鸟”为主题的远足活动.已知学校与某岛相距24千米,远足服务人员骑自行车,学生步行,服务人员骑自行车的平均速度是学生步行平均速度的2.5倍,服务人员与学生同时从学校出发,到达某君山岛时,服务人员所花时间比学生少用了3.6小时,求学生步行的平均速度是多少千米/小时.
专题解读
设学生步行的平均速度是每小时x千米.服务人员骑自行车的平均速度是每小时2.5x千米,
根据题意: - =3.6,解得:x=4,
经检验,x=4是所列方程的解,且符合题意.答:学生步行的平均速度是每小时4千米.
24
x
24 2.5x
专题解读
14.几个小伙伴打算去音乐厅观看演出,他们准备用360元钱购买门票.下面是两个小伙伴的对话:
根据对话的内容,请你求出小伙伴们的人数.
专题解读
解:设票价为x元,由题意得, =
+2,解得:x=60,经检验,x=60是原分式方程的解.则小伙伴的人数为:
+2=8. 答:小伙伴们的人数为8人.
360-72
0.6x
360
x
360
x
专题解读
15.一项工程,甲、乙两公司合作,12天可以完成,共需付工费100 800元,如果甲、乙两公司单独完成此项工程,乙公司所用时间是甲公司的1.5倍,乙公司每天的施工费比甲公司每天的施工费少1 600元.
(1)甲、乙公司单独完成此项工程,各需多少天?
(2)若让一个公司单独完成这项工程,哪个公司施工费较少?
专题解读
(1)设甲公司单独完成此项工程需x天,则乙公司单独完成此项工程需1.5x天.根据题意,得
或 解得x=20,经检验知x=20是方程的解. ∴1.5x=30.答略.
(2)设甲公司每天的施工费为y元,则乙公司每天的施工费为(y-1 600)元,根据题意得12(y+y-1 600)=100 800,解得y=5 000,甲公司单独完成此项工程所需的施工费:20×5 000=100 000(元);
乙公司单独完成此项工程所需的施工费:30×(5 000-1 600)=102 000(元);故甲公司的施工费较少.
专题解读
16.湛茂高速铁路湛江段正在建设中,甲、乙两个工程队计划参与一项工程建设,甲队单独施工30天完成该项工程的 ,这时乙队加入,两队还需同时施工15天,才能完成该项工程.
(1)若乙队单独施工,需要多少天才能完成该项工程?
(2)若甲队参与该项工程施工的时间不超过36天,则乙队至少施工多少天才能完成该项工程?
专题解读
(1)设乙队单独施工,需要x天才能完成该项工程,∵甲队单独施工30天完成该项工程的 ,∴甲队单独施工30÷ =90天完成该项工程,根据题意可得: +15 =1,解得:x=30,检验得:x=30是原方程的根,答:乙队单独施工,需要30天才能完成该项工程;
1
3
1
3
1
3
( + )
1
90
1
x
专题解读
(2)设乙队参与施工y天才能完成该项工程,根据题意可得: ×36+ y≥1,解得:y≥18,答:乙队至少施工18天才能完成该项工程.
1
90
1
30
专题解读
17.近年来雾霾天气给人们的生活带来很大影响,空气质量问题倍受人们关注.某单位计划在室内安装空气净化装置,需购进A、B两种设备.每台B种设备价格比每台A种设备价格多0.7万元,花3万元购买A种设备和花7.2万元购买B种设备的数量相同.
(1)求A种、B种设备每台各多少万元?
(2)根据单位实际情况,需购进A、B两种设备共20台,总费用不高于15万元,求A种设备至少要购买多少台?
专题解读
(1)设每台A种设备x万元,则每台B种设备
(x+0.7)万元,根据题意得: = ,
解得:x=0.5. 经检验,x=0.5是原方程的解,∴x+0.7=1.2. 答:每台A种设备0.5万元,每台B种设备1.2万元.
3
x
7.2
x+0.7
专题解读
(2)设购买A种设备m台,则购买B种设备(20-m)台,根据题意得:0.5m+1.2(20-m)≤15,
解得:m≥ .∵m为整数,∴m≥13.答:A种
设备至少要购买13台.
90
7
专题解读
18.某车行经销的A型自行车去年6月份销售总额为1.6万元,今年由于改造升级每辆车售价比去年增加200元,今年6月份与去年同期相比,销售数量相同,销售总额增加25%.
(1)求今年A型车每辆售价多少元?
(2)该车行计划7月份用不超过4.3万元的资金新进一批A型车和B型车共50辆,应如何进货才能使这批车售完后获利最多?
今年A,B两种型号车的进价和售价如下表:
A型车 B型车
进价(元/辆) 800 950
售价(元/辆) 今年售价 1200
专题解读
(1)设今年A型车每辆售价为x元,则去年A型车每辆售价为(x-200)元,根据题意得:
= ,解得:x=1000,经检验,x=1000是原分式方程的解.
答:今年A型车每辆售价为1000元.
1.6
x-200
1.6×(1+25%)
x
专题解读
(2)设购进A型车m辆,则购进B型车(50-m)辆,根据题意得:800m+950(50-m)≤43000,解得:m≥30.销售利润为(100-800)m+(1200-950)(50-m)=-50m+12500,∵-50<0,∴当m=30时,销售利润最多.答:当购进A型车30辆、购进B型车20辆时,才能使这批车售完后获利最多.
