华师大版八年级下册11.5分式方程的解法复习
文档属性
| 名称 | 华师大版八年级下册11.5分式方程的解法复习 |  | |
| 格式 | zip | ||
| 文件大小 | 577.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-11-03 19:25:01 | ||
图片预览




文档简介
课件11张PPT。华师版八年级下
分式方程的解法(复习课)学习目标:2、能熟练地解可化为一元一次方程的分式方程3、理解增根产生的原因,能够利用增根解决相关问题 1、进一步理解分式方程的概念,能熟练对方程是否是
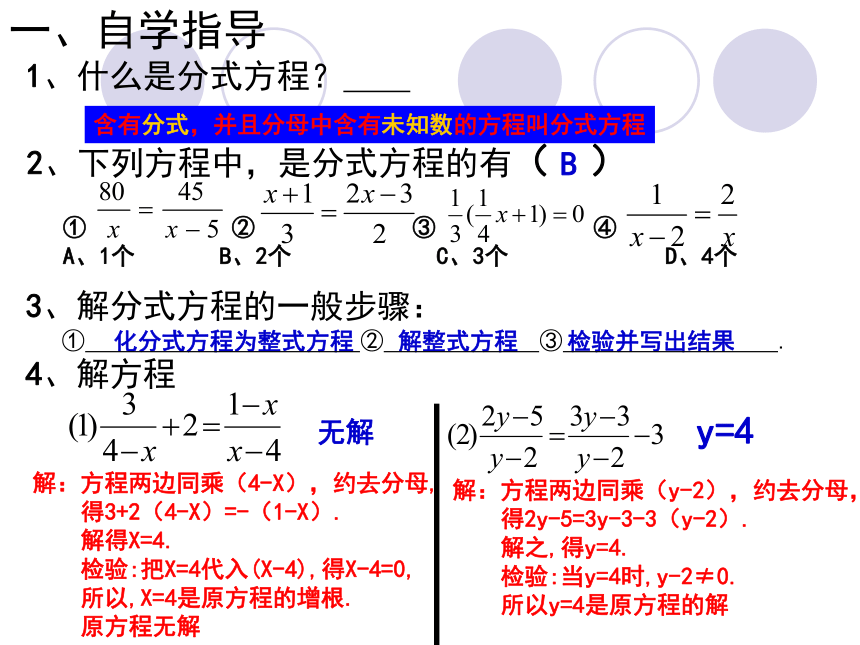
分式方程作出正确判断一、自学指导1、什么是分式方程? 含有分式,并且分母中含有未知数的方程叫分式方程3、解分式方程的一般步骤:
① ② ③ .
2、下列方程中,是分式方程的有( )
① ② ③ ④
A、1个 B、2个 C、3个 D、4个B4、解方程解:方程两边同乘(4-X),约去分母,
得3+2(4-X)=-(1-X).
解得X=4.
检验:把X=4代入(X-4),得X-4=0,
所以,X=4是原方程的增根.
原方程无解 解:方程两边同乘(y-2),约去分母,
得2y-5=3y-3-3(y-2).
解之,得y=4.
检验:当y=4时,y-2≠0.
所以y=4是原方程的解[错因分析与解题指导]:
在方程两边同乘(x-2)时,右边-3项漏乘了最简公分母.
去分母时,特别要当心原方程中原来“没有分母”(其实是分母为1)的项,
不要漏乘. D[错因分析与解题指导]:
在解分式方程时,最后忘记对所求整式方程的解进行检验,把该解错写
成原分式方程的解.解分式方程时,可能会产生增根,所以验根在求解分式方程
过程中是不可缺少的步骤,不能漏掉6、解分式方程 分以下四步,其中错误的一步是( )
A、各分式的最简公分母是(X+1)(X-1);
B、方程两边都乘以(X+1)(X-1),得变式方程2(X-1)+3(X+1)=6;
C、解这个整式方程,得X=1;
D、所以原方程的解为X=1
原因:我们在把分式方程转化为整式方程过程中,
无形中去掉了原分式方程中分母不为零的限制条件,从而
扩大了未知数的取值范围,于时就有可能产生了满足整式
方程而不满足分式方程的根,即增根。
方法:将所求的整式方程的根代入最简公分母,看它
的值是否为零。如果为零,即为增根;如果不为零,则为
原方程的根。7、解分式方程出现增根的原因是什么?如何检验解出的是增根或是原方程的根?点石成金:
增根的特征:
①、一定是分式方程所化成整式方程的根
②、能使最简公分母为零
利用上述增根特征可以解决与增根相关的问题
8、若关于X的方程 有增根,则增根为 .X=3 或 X=-39、(体验过程题)题目:当a为何值时,关于x的方程 有增根?
解:原方程的两边同乘以(x-2),去分母,得 . ……… ①
因为分式方程有增根,且增根为 ,
把x=2代入① 式,得 ,
所以当 时, 有增根.
10、若关于X的方程 无解,求 的值 解:去分母整理得,
解之,得
因为方程无解,所以 为方程的增根,
又由于方程的增根为X=3,所以 即点
石
成
金
你能概括出利用增根求解分式方程中待定字母
的值题目的一般步骤吗?1、把分式方程化成整式方程;
2、令最简公分母为0,求出X的值;
3、再把X的值代入整式方程,求出待定字母的值。
二、当堂训练1、把分式方程 化为整式方程得( )
A、x+2=-1 B、x+2(x-2)=1 C、x+2(x-2)=-1 D、x+2=1
2、解方程
⑴ ⑵CX=23、若关于X的方程 有增根,则增根
是多少?并求方程产生增根是m的值。解:因为方程有增根,所以有 ,所以 或
方程两边同时乘以 ,去分母得
当 时, ,
当 时, ,
所以方程的增根 或
当 时,产生增根
当 时,产生增根 3或-36或12无解三、课堂小结通过本节课的学习,谈一谈你有哪些收获?四、课后作业(98西安)解方程:欢迎各位老师莅临指导
谢谢大家!
分式方程的解法(复习课)学习目标:2、能熟练地解可化为一元一次方程的分式方程3、理解增根产生的原因,能够利用增根解决相关问题 1、进一步理解分式方程的概念,能熟练对方程是否是
分式方程作出正确判断一、自学指导1、什么是分式方程? 含有分式,并且分母中含有未知数的方程叫分式方程3、解分式方程的一般步骤:
① ② ③ .
2、下列方程中,是分式方程的有( )
① ② ③ ④
A、1个 B、2个 C、3个 D、4个B4、解方程解:方程两边同乘(4-X),约去分母,
得3+2(4-X)=-(1-X).
解得X=4.
检验:把X=4代入(X-4),得X-4=0,
所以,X=4是原方程的增根.
原方程无解 解:方程两边同乘(y-2),约去分母,
得2y-5=3y-3-3(y-2).
解之,得y=4.
检验:当y=4时,y-2≠0.
所以y=4是原方程的解[错因分析与解题指导]:
在方程两边同乘(x-2)时,右边-3项漏乘了最简公分母.
去分母时,特别要当心原方程中原来“没有分母”(其实是分母为1)的项,
不要漏乘. D[错因分析与解题指导]:
在解分式方程时,最后忘记对所求整式方程的解进行检验,把该解错写
成原分式方程的解.解分式方程时,可能会产生增根,所以验根在求解分式方程
过程中是不可缺少的步骤,不能漏掉6、解分式方程 分以下四步,其中错误的一步是( )
A、各分式的最简公分母是(X+1)(X-1);
B、方程两边都乘以(X+1)(X-1),得变式方程2(X-1)+3(X+1)=6;
C、解这个整式方程,得X=1;
D、所以原方程的解为X=1
原因:我们在把分式方程转化为整式方程过程中,
无形中去掉了原分式方程中分母不为零的限制条件,从而
扩大了未知数的取值范围,于时就有可能产生了满足整式
方程而不满足分式方程的根,即增根。
方法:将所求的整式方程的根代入最简公分母,看它
的值是否为零。如果为零,即为增根;如果不为零,则为
原方程的根。7、解分式方程出现增根的原因是什么?如何检验解出的是增根或是原方程的根?点石成金:
增根的特征:
①、一定是分式方程所化成整式方程的根
②、能使最简公分母为零
利用上述增根特征可以解决与增根相关的问题
8、若关于X的方程 有增根,则增根为 .X=3 或 X=-39、(体验过程题)题目:当a为何值时,关于x的方程 有增根?
解:原方程的两边同乘以(x-2),去分母,得 . ……… ①
因为分式方程有增根,且增根为 ,
把x=2代入① 式,得 ,
所以当 时, 有增根.
10、若关于X的方程 无解,求 的值 解:去分母整理得,
解之,得
因为方程无解,所以 为方程的增根,
又由于方程的增根为X=3,所以 即点
石
成
金
你能概括出利用增根求解分式方程中待定字母
的值题目的一般步骤吗?1、把分式方程化成整式方程;
2、令最简公分母为0,求出X的值;
3、再把X的值代入整式方程,求出待定字母的值。
二、当堂训练1、把分式方程 化为整式方程得( )
A、x+2=-1 B、x+2(x-2)=1 C、x+2(x-2)=-1 D、x+2=1
2、解方程
⑴ ⑵CX=23、若关于X的方程 有增根,则增根
是多少?并求方程产生增根是m的值。解:因为方程有增根,所以有 ,所以 或
方程两边同时乘以 ,去分母得
当 时, ,
当 时, ,
所以方程的增根 或
当 时,产生增根
当 时,产生增根 3或-36或12无解三、课堂小结通过本节课的学习,谈一谈你有哪些收获?四、课后作业(98西安)解方程:欢迎各位老师莅临指导
谢谢大家!
