2021-2022学年高二上学期数学人教A版(2019)选择性必修第三册6.2.3组合课件(18张ppt)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教A版(2019)选择性必修第三册6.2.3组合课件(18张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 2.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-03 16:14:41 | ||
图片预览






文档简介
(共18张PPT)
探究1: 从甲、乙、丙3名同学中选出2名同学。 (1)选两名同学参一项活动, 有多少种不同选法?
(2)若这两名同学分别参加上、下午的一项活动, 又有多少种选法?
(3)第1,2问选法上有什么区别?
问题探究
从n个不同元素中取出 m ( m ≤ n )个元素, 叫做从n个不同元素中取出m个元素的一个组合。
从n个不同元素中取出 m ( m ≤ n )个元素的所有不同组合的个数,叫做从n个不同元素中取出m个元素的组合数,用 表示,也可以用符号 表示。
知识归纳
思考: 排列和组合之间的联系和区别是什么?
思考: 排列和组合之间的联系和区别是什么?
联系:
两者都是从n个元素中取出m个元素
区别:
1、排列和顺序相关,组合和顺序无关;
2、元素相同且顺序也相同,排列才相同;
元素相同,不管顺序是否相同,组合就是相同的。
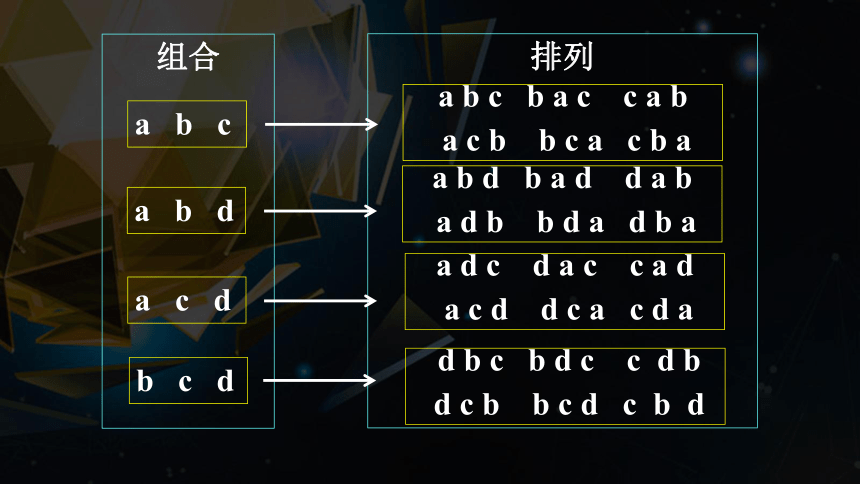
探究2. 从a、b、c、d这4个元素中取出3个不同元素 (1)将这3个不同元素形成一个组合, 则不同的组合有多少种? (2)将这3个不同元素形成一个排列, 则不同的排列有多少种?
a b c
a b d
a c d
b c d
组合
排列
a b c b a c c a b
a c b b c a c b a
a b d b a d d a b
a d b b d a d b a
a d c d a c c a d
a c d d c a c d a
d b c b d c c d b
d c b b c d c b d
知识归纳
一般的,从n个不同元素取出m个元素的排列数可以看成:
1、从n个元素中取出m个元素,共
2、将取出m个元素做全排列,共
运用1. ①计算:
新知运用
运用2.
运用2.
运用2.
[例1] (1)平面内有10个点, 以其中每2个点为端点的线段共有多少条? (2)平面内有10个点, 以其中每2个点为端点的有向线段共有多少条?
[例2] 在100件产品中, 有98件合格品,2件次品。从这100件产品中任意抽取3件。 (1)有多少种不同抽法? (2)抽出的3件中恰好有1件是次品的抽法有多少种? (3)抽出的3件中至少有1件是次品的抽法有多少种?
运用3. 一位教练的足球队共有17名初级学员,他们中以前没有一个参加比赛,按照足球规则,比赛时一个足球队的上场队员是11人,问:
(1) 这位教练从17名学员中可以形成多少种上场方案?
(2) 如果在选出11名队员时还要确定其中的守门员,则教练员有多少种方式做这件事?
[例3] 甲乙丙3项任务,甲需2人承担,乙、丙各需1人承担,从10人中选派4人承担3项任务,不同选法有 ( )
A.1260 B.2025
C.2520 D.5040
C
探究1: 从甲、乙、丙3名同学中选出2名同学。 (1)选两名同学参一项活动, 有多少种不同选法?
(2)若这两名同学分别参加上、下午的一项活动, 又有多少种选法?
(3)第1,2问选法上有什么区别?
问题探究
从n个不同元素中取出 m ( m ≤ n )个元素, 叫做从n个不同元素中取出m个元素的一个组合。
从n个不同元素中取出 m ( m ≤ n )个元素的所有不同组合的个数,叫做从n个不同元素中取出m个元素的组合数,用 表示,也可以用符号 表示。
知识归纳
思考: 排列和组合之间的联系和区别是什么?
思考: 排列和组合之间的联系和区别是什么?
联系:
两者都是从n个元素中取出m个元素
区别:
1、排列和顺序相关,组合和顺序无关;
2、元素相同且顺序也相同,排列才相同;
元素相同,不管顺序是否相同,组合就是相同的。
探究2. 从a、b、c、d这4个元素中取出3个不同元素 (1)将这3个不同元素形成一个组合, 则不同的组合有多少种? (2)将这3个不同元素形成一个排列, 则不同的排列有多少种?
a b c
a b d
a c d
b c d
组合
排列
a b c b a c c a b
a c b b c a c b a
a b d b a d d a b
a d b b d a d b a
a d c d a c c a d
a c d d c a c d a
d b c b d c c d b
d c b b c d c b d
知识归纳
一般的,从n个不同元素取出m个元素的排列数可以看成:
1、从n个元素中取出m个元素,共
2、将取出m个元素做全排列,共
运用1. ①计算:
新知运用
运用2.
运用2.
运用2.
[例1] (1)平面内有10个点, 以其中每2个点为端点的线段共有多少条? (2)平面内有10个点, 以其中每2个点为端点的有向线段共有多少条?
[例2] 在100件产品中, 有98件合格品,2件次品。从这100件产品中任意抽取3件。 (1)有多少种不同抽法? (2)抽出的3件中恰好有1件是次品的抽法有多少种? (3)抽出的3件中至少有1件是次品的抽法有多少种?
运用3. 一位教练的足球队共有17名初级学员,他们中以前没有一个参加比赛,按照足球规则,比赛时一个足球队的上场队员是11人,问:
(1) 这位教练从17名学员中可以形成多少种上场方案?
(2) 如果在选出11名队员时还要确定其中的守门员,则教练员有多少种方式做这件事?
[例3] 甲乙丙3项任务,甲需2人承担,乙、丙各需1人承担,从10人中选派4人承担3项任务,不同选法有 ( )
A.1260 B.2025
C.2520 D.5040
C
