2021-2022学年高二上学期数学人教版(2019)选择性必修第二册5.3.2函数的极值与最大(小)值---函数的极值课件(32张ppt)
文档属性
| 名称 | 2021-2022学年高二上学期数学人教版(2019)选择性必修第二册5.3.2函数的极值与最大(小)值---函数的极值课件(32张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 697.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-03 16:15:56 | ||
图片预览








文档简介
(共32张PPT)
函数的极值与最大(小)值
---函数的极值
设函数y=f(x)在某个区间内有导数,如果在这个区间内y'>0,那么函数y=f(x)为这个区间内的增函数;如果在这个区间内y'<0,那么函数y=f(x)为这个区间内的减函数.
1.函数的导数与函数的单调性的关系:
(1) 确定函数f(x)的定义域; (2) 求出函数的导数f '(x); (3) 解不等式f '(x)>0,得函数递增区间; 解不等式f '(x)<0,得函数递减区间.
2.用导数求函数单调区间的步骤:
探究(一):函数极值的有关概念
探究(一):函数极值的有关概念
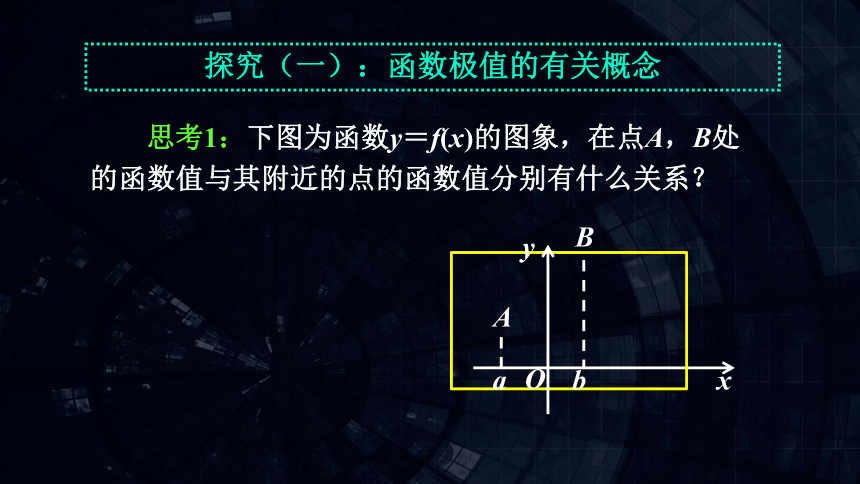
思考1:下图为函数y=f(x)的图象,在点A,B处的函数值与其附近的点的函数值分别有什么关系?
B
A
O
x
y
a
b
探究(一):函数极值的有关概念
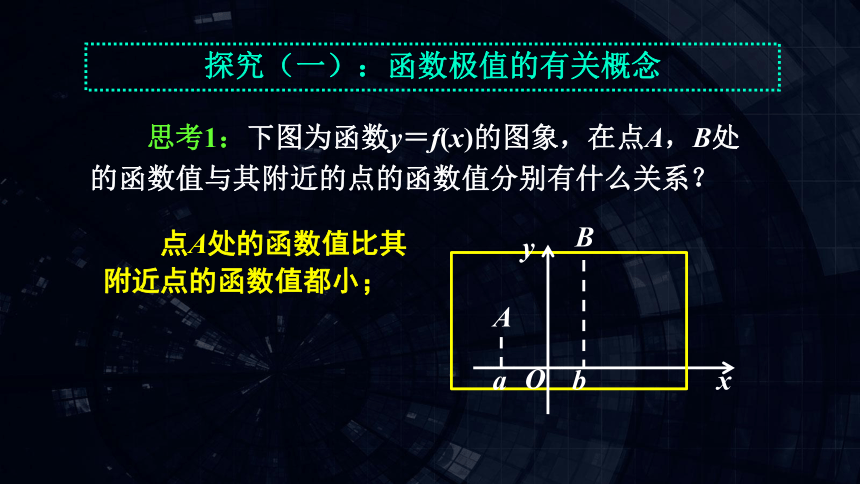
思考1:下图为函数y=f(x)的图象,在点A,B处的函数值与其附近的点的函数值分别有什么关系?
B
A
O
x
y
a
b
点A处的函数值比其 附近点的函数值都小;
探究(一):函数极值的有关概念
思考1:下图为函数y=f(x)的图象,在点A,B处的函数值与其附近的点的函数值分别有什么关系?
B
A
O
x
y
a
b
点A处的函数值比其 附近点的函数值都小;
点B处的函数值比其 附近点的函数值都大.
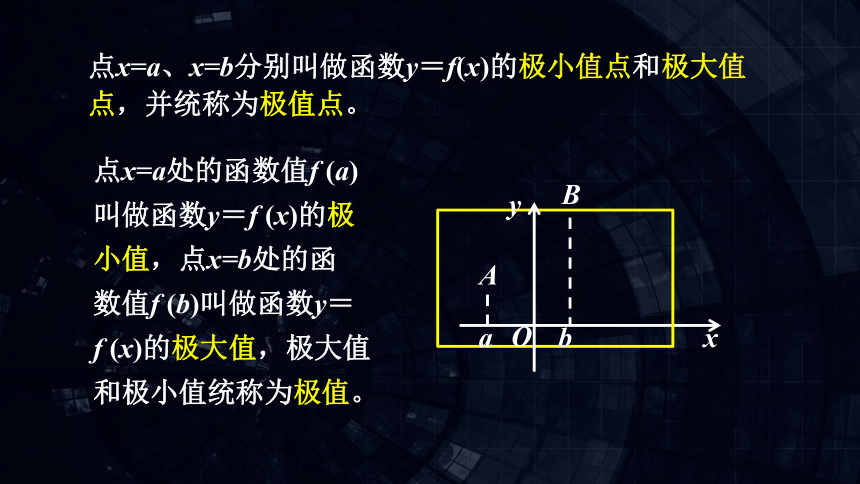
点x=a、x=b分别叫做函数y=f(x)的极小值点和极大值点,并统称为极值点。
B
A
O
x
y
a
b
点x=a处的函数值f (a)
叫做函数y=f (x)的极
小值,点x=b处的函
数值f (b)叫做函数y=
f (x)的极大值,极大值
和极小值统称为极值。
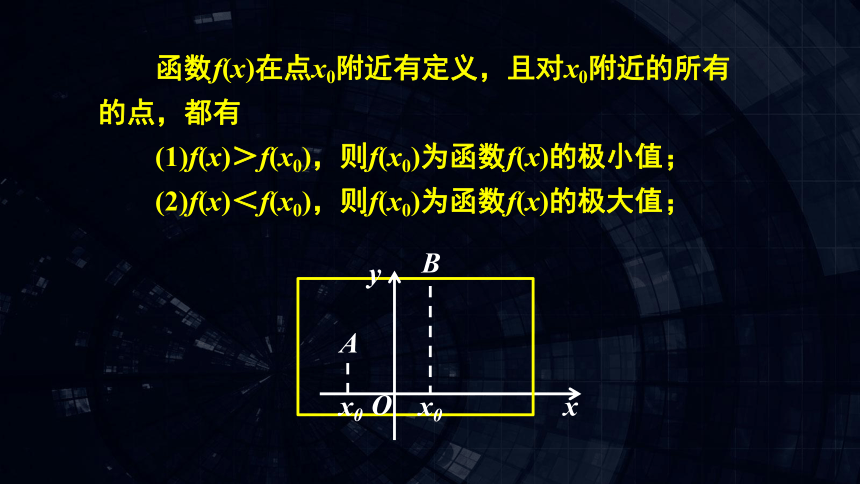
函数f(x)在点x0附近有定义,且对x0附近的所有的点,都有
(1)f(x)>f(x0),则f(x0)为函数f(x)的极小值;
(2)f(x)<f(x0),则f(x0)为函数f(x)的极大值;
B
A
O
x
y
x0
x0
思考2:函数的极大值都比极小值大吗?
思考2:函数的极大值都比极小值大吗?
O
x
y
A
B
思考2:函数的极大值都比极小值大吗?
不一定
O
x
y
A
B
探究(二):函数极值的判定原理
探究(二):函数极值的判定原理
思考1:下图中,在极大值点A左右两侧函数的单调性分别如何?
在x0附近,当x<x0,x>x0,x=x0时, f′(x0)的取值如何变化?
A
y=f(x)
O
x
y
x0
探究(二):函数极值的判定原理
思考1:下图中,在极大值点A左右两侧函数的单调性分别如何?
在x0附近,当x<x0,x>x0,x=x0时, f′(x0)的取值如何变化?
A
y=f(x)
O
x
y
x0
左侧递增,右侧递减.
在x0附近左侧f′(x)>0,
右侧f′(x)<0,则f(x0)
是极大值.
思考3:下图中,在极小点值点B左右两侧函数的单调性分别如何?
在x0附近,当x<x0,x>x0,x=x0时,f′(x0)的取值如何变化?
B
y=f(x)
O
x
y
x0
思考3:下图中,在极小点值点B左右两侧函数的单调性分别如何?
在x0附近,当x<x0,x>x0,x=x0时,f′(x0)的取值如何变化?
B
y=f(x)
O
x
y
x0
左侧递减,右侧递增.
在x0附近左侧f′(x)<0,
右侧f′(x)>0,则f(x0)
是极小值.
思考5:函数f(x)在极值点的导数一定为0吗?导数为0的点一定是极值点吗?
思考5:函数f(x)在极值点的导数一定为0吗?导数为0的点一定是极值点吗?
可导函数在极值点的导数一定为0,导数为0的点不一定是极值点(可疑点).
如果函数y=f(x)的导函数在(a,b)的图象如图所示,则函数y=f(x)在区间(a,b)内极小值点个数为_______
如果函数y=f(x)的导函数的图象如图所示,给出下列判断:
①函数y=f(x)在区间 内单调递增;
②函数y=f(x)在区间 内单调递减;
③函数y=f(x)在区间 ( 4 , 5 ) 内单调递增;
④当x=2时,函数y=f(x)有极小值;
⑤当x= 时,函数y=f(x)有极大值.
则上述判断中正确的是_________
[例1]
(2)求y=(x2 1)3+1的极值.
[例2]
求极值的具体步骤: 第一:求导数f '(x). 第二:令f '(x)=0,求方程的根. 第三:列表,检查f '(x)在方程根左右的值的符号,如果左正右负,那么f(x)在这个根处取得极大值;如果左负右正,那么f(x)在这个根处取得极小值;如果左右都是正,或者左右都是负,那么f(x)在这个根处无极值. 如果函数在某些点处连续但不可导,也需要考虑这些点是否是极值点.
已知函数 f(x)= x3+ax2+b. 若函数f(x)在x=0,x=4处取得极值,且极小值为 1,求a、b的值;
[例2]
已知函数 f(x)= x3+ax2+b. 若函数f(x)在x=0,x=4处取得极值,且极小值为 1,求a、b的值;
已知函数f(x)=x3-a(2x-1)在区间(0,1)内存在极小值,求实数a的取值范围.
[例2]
[变式训练]
1.函数的极大、极小值的定义以及判别方法.
2.求可导函数f(x)的极值的三个步骤.
3.还有要弄清楚函数的极值是就函数在某一点附近的小区间而言的,在整个定义区间可能有多个极值,且要在这点处连续.
4. 可导函数极值点的导数为0,但导数为零的点不一定是极值点,要看这点两侧的导数是否异号.
5. 函数的不可导点可能是极值点.
函数的极值与最大(小)值
---函数的极值
设函数y=f(x)在某个区间内有导数,如果在这个区间内y'>0,那么函数y=f(x)为这个区间内的增函数;如果在这个区间内y'<0,那么函数y=f(x)为这个区间内的减函数.
1.函数的导数与函数的单调性的关系:
(1) 确定函数f(x)的定义域; (2) 求出函数的导数f '(x); (3) 解不等式f '(x)>0,得函数递增区间; 解不等式f '(x)<0,得函数递减区间.
2.用导数求函数单调区间的步骤:
探究(一):函数极值的有关概念
探究(一):函数极值的有关概念
思考1:下图为函数y=f(x)的图象,在点A,B处的函数值与其附近的点的函数值分别有什么关系?
B
A
O
x
y
a
b
探究(一):函数极值的有关概念
思考1:下图为函数y=f(x)的图象,在点A,B处的函数值与其附近的点的函数值分别有什么关系?
B
A
O
x
y
a
b
点A处的函数值比其 附近点的函数值都小;
探究(一):函数极值的有关概念
思考1:下图为函数y=f(x)的图象,在点A,B处的函数值与其附近的点的函数值分别有什么关系?
B
A
O
x
y
a
b
点A处的函数值比其 附近点的函数值都小;
点B处的函数值比其 附近点的函数值都大.
点x=a、x=b分别叫做函数y=f(x)的极小值点和极大值点,并统称为极值点。
B
A
O
x
y
a
b
点x=a处的函数值f (a)
叫做函数y=f (x)的极
小值,点x=b处的函
数值f (b)叫做函数y=
f (x)的极大值,极大值
和极小值统称为极值。
函数f(x)在点x0附近有定义,且对x0附近的所有的点,都有
(1)f(x)>f(x0),则f(x0)为函数f(x)的极小值;
(2)f(x)<f(x0),则f(x0)为函数f(x)的极大值;
B
A
O
x
y
x0
x0
思考2:函数的极大值都比极小值大吗?
思考2:函数的极大值都比极小值大吗?
O
x
y
A
B
思考2:函数的极大值都比极小值大吗?
不一定
O
x
y
A
B
探究(二):函数极值的判定原理
探究(二):函数极值的判定原理
思考1:下图中,在极大值点A左右两侧函数的单调性分别如何?
在x0附近,当x<x0,x>x0,x=x0时, f′(x0)的取值如何变化?
A
y=f(x)
O
x
y
x0
探究(二):函数极值的判定原理
思考1:下图中,在极大值点A左右两侧函数的单调性分别如何?
在x0附近,当x<x0,x>x0,x=x0时, f′(x0)的取值如何变化?
A
y=f(x)
O
x
y
x0
左侧递增,右侧递减.
在x0附近左侧f′(x)>0,
右侧f′(x)<0,则f(x0)
是极大值.
思考3:下图中,在极小点值点B左右两侧函数的单调性分别如何?
在x0附近,当x<x0,x>x0,x=x0时,f′(x0)的取值如何变化?
B
y=f(x)
O
x
y
x0
思考3:下图中,在极小点值点B左右两侧函数的单调性分别如何?
在x0附近,当x<x0,x>x0,x=x0时,f′(x0)的取值如何变化?
B
y=f(x)
O
x
y
x0
左侧递减,右侧递增.
在x0附近左侧f′(x)<0,
右侧f′(x)>0,则f(x0)
是极小值.
思考5:函数f(x)在极值点的导数一定为0吗?导数为0的点一定是极值点吗?
思考5:函数f(x)在极值点的导数一定为0吗?导数为0的点一定是极值点吗?
可导函数在极值点的导数一定为0,导数为0的点不一定是极值点(可疑点).
如果函数y=f(x)的导函数在(a,b)的图象如图所示,则函数y=f(x)在区间(a,b)内极小值点个数为_______
如果函数y=f(x)的导函数的图象如图所示,给出下列判断:
①函数y=f(x)在区间 内单调递增;
②函数y=f(x)在区间 内单调递减;
③函数y=f(x)在区间 ( 4 , 5 ) 内单调递增;
④当x=2时,函数y=f(x)有极小值;
⑤当x= 时,函数y=f(x)有极大值.
则上述判断中正确的是_________
[例1]
(2)求y=(x2 1)3+1的极值.
[例2]
求极值的具体步骤: 第一:求导数f '(x). 第二:令f '(x)=0,求方程的根. 第三:列表,检查f '(x)在方程根左右的值的符号,如果左正右负,那么f(x)在这个根处取得极大值;如果左负右正,那么f(x)在这个根处取得极小值;如果左右都是正,或者左右都是负,那么f(x)在这个根处无极值. 如果函数在某些点处连续但不可导,也需要考虑这些点是否是极值点.
已知函数 f(x)= x3+ax2+b. 若函数f(x)在x=0,x=4处取得极值,且极小值为 1,求a、b的值;
[例2]
已知函数 f(x)= x3+ax2+b. 若函数f(x)在x=0,x=4处取得极值,且极小值为 1,求a、b的值;
已知函数f(x)=x3-a(2x-1)在区间(0,1)内存在极小值,求实数a的取值范围.
[例2]
[变式训练]
1.函数的极大、极小值的定义以及判别方法.
2.求可导函数f(x)的极值的三个步骤.
3.还有要弄清楚函数的极值是就函数在某一点附近的小区间而言的,在整个定义区间可能有多个极值,且要在这点处连续.
4. 可导函数极值点的导数为0,但导数为零的点不一定是极值点,要看这点两侧的导数是否异号.
5. 函数的不可导点可能是极值点.
