诱导公式(2)
图片预览


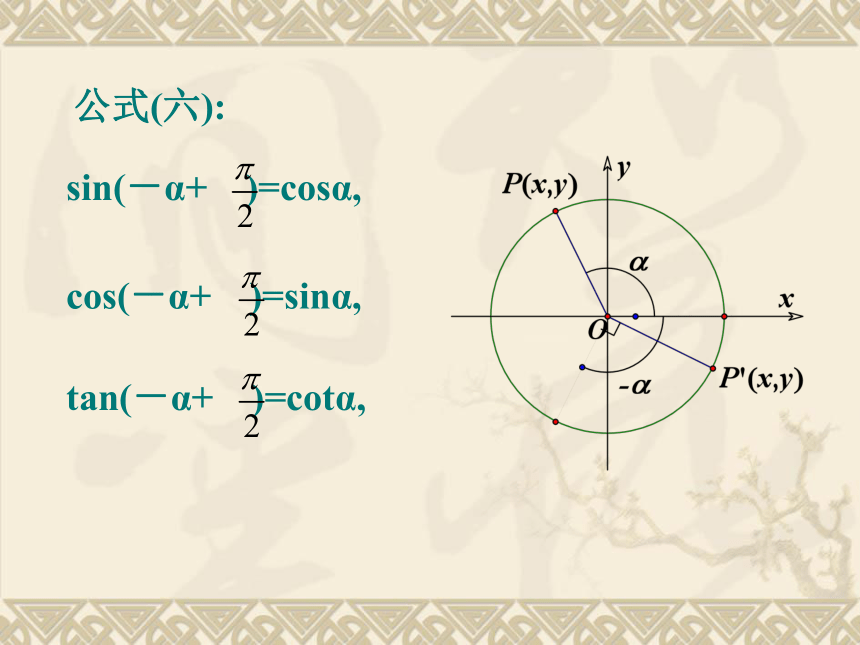




文档简介
课件19张PPT。1.2.4 诱导公式(二)公式(五):sin(α+ )=cosα,cos(α+ )=-sinα,tan(α+ )=-cotα, 这是因为,若设α的终边与单位圆交于点P(x,y),则角α+ 的终边与单位圆的交点必为P′(-y,x). 由三角函数的定义可得公式(四).公式(六):sin(-α+ )=cosα,cos(-α+ )=sinα,tan(-α+ )=cotα,四组诱导公式的作用 :任意一个角都可以表示为
的形式。 这样由前面的公式就可以把任意角的三角函数求值问题转化为0到 之间角的三角函数求值问题。 这样,诱导公式可以分为两大组:
(1) 由2kπ+α,-α,π+α,π-α等为一组,所得到的三角函数与原来的三角函数是相同三角函数;(2)由 +α, -α为一组,所得到的三角函数与原来的三角函数是互余的三角函数;记忆口诀:奇变偶不变. 所有的诱导公式的符号是由角度所在象限决定的,即把角α看做锐角,原来角度所在象限,原来函数所具有的符号为公式右边的符号。记忆口诀:符号看象限.例1 求证:证: 左边 = 右边 .∴ 原等式成立 .例2.解:=1.例3 .已知sinβ= ,sin(α+β)=1,求sin(2α+β).解: 从而 =sin(π-β)
=sinβ=例4. 已知f(cosx)=cos17x,求f(sinx)解:f(sinx)=f[cos(90?-x)]
=cos[17×(90?-x)]
=cos(4×360?+90?-17x)
=cos(90?-17x)
=sin17x.课堂练习: 1.计算:sin315??sin(?480?)+cos(?330?) .解:原式 = sin(360??45?) + sin(360?+120?) + cos(?360?+30?) = ?sin45? + sin60? + cos30? 2.已知解:3.求证:证:若k是偶数,即k = 2n (n?Z) 则:=-1若k是奇数,即k = 2n + 1 (n?Z) 则: =-1∴原式成立. 5.已知:解:由题设:由此:当a ? 0时,tan? < 0, cos? < 0, ?为第二象限角, 当a = 0时,tan? = 0, ? = k?, ∴cos? = ±1,
∵ cos ?≤0, ∴cos? = ?1 , 综上所述: 6.若关于x的方程2cos2(? + x) ? sinx + a = 0 有实根,求实数a的取值范围。 解:原方程变形为:2cos2x ? sinx + a = 0 ,
即 2 ? 2sin2x ? sinx + a = 0∴ ∵? 1≤sinx≤1 ∴ ∴ a的取值范围是[ ].小结: 应用诱导公式化简三角函数的一般步骤:
1? 用“? ?”公式化为正角的三角函数;
2? 用“2k? + ?”公式化为[0,2?]角的三角函数;
3? 用“?±?”或“2? ? ?”公式化为锐角的三角函数.
的形式。 这样由前面的公式就可以把任意角的三角函数求值问题转化为0到 之间角的三角函数求值问题。 这样,诱导公式可以分为两大组:
(1) 由2kπ+α,-α,π+α,π-α等为一组,所得到的三角函数与原来的三角函数是相同三角函数;(2)由 +α, -α为一组,所得到的三角函数与原来的三角函数是互余的三角函数;记忆口诀:奇变偶不变. 所有的诱导公式的符号是由角度所在象限决定的,即把角α看做锐角,原来角度所在象限,原来函数所具有的符号为公式右边的符号。记忆口诀:符号看象限.例1 求证:证: 左边 = 右边 .∴ 原等式成立 .例2.解:=1.例3 .已知sinβ= ,sin(α+β)=1,求sin(2α+β).解: 从而 =sin(π-β)
=sinβ=例4. 已知f(cosx)=cos17x,求f(sinx)解:f(sinx)=f[cos(90?-x)]
=cos[17×(90?-x)]
=cos(4×360?+90?-17x)
=cos(90?-17x)
=sin17x.课堂练习: 1.计算:sin315??sin(?480?)+cos(?330?) .解:原式 = sin(360??45?) + sin(360?+120?) + cos(?360?+30?) = ?sin45? + sin60? + cos30? 2.已知解:3.求证:证:若k是偶数,即k = 2n (n?Z) 则:=-1若k是奇数,即k = 2n + 1 (n?Z) 则: =-1∴原式成立. 5.已知:解:由题设:由此:当a ? 0时,tan? < 0, cos? < 0, ?为第二象限角, 当a = 0时,tan? = 0, ? = k?, ∴cos? = ±1,
∵ cos ?≤0, ∴cos? = ?1 , 综上所述: 6.若关于x的方程2cos2(? + x) ? sinx + a = 0 有实根,求实数a的取值范围。 解:原方程变形为:2cos2x ? sinx + a = 0 ,
即 2 ? 2sin2x ? sinx + a = 0∴ ∵? 1≤sinx≤1 ∴ ∴ a的取值范围是[ ].小结: 应用诱导公式化简三角函数的一般步骤:
1? 用“? ?”公式化为正角的三角函数;
2? 用“2k? + ?”公式化为[0,2?]角的三角函数;
3? 用“?±?”或“2? ? ?”公式化为锐角的三角函数.
