2021-2022学年人教版七年级数学上册2.2整式的加减-合并同类项课件(共16张PPT)
文档属性
| 名称 | 2021-2022学年人教版七年级数学上册2.2整式的加减-合并同类项课件(共16张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-04 16:37:31 | ||
图片预览






文档简介
(共16张PPT)
2.2整式的加减(1)
----合并同类项
1.理解同类项的概念
2.学会合并同类项
学习目标
如图:超市里新到的水果上架时怎样摆放呢?
情境导入:
8a
5a
5x2y
3x2y
6xy
-3xy
将下列单项式进行分类,并与同伴交流一下你为什么这么分类?
8a
3x2y
5x2y
-3xy
5a
6xy
探究新知:
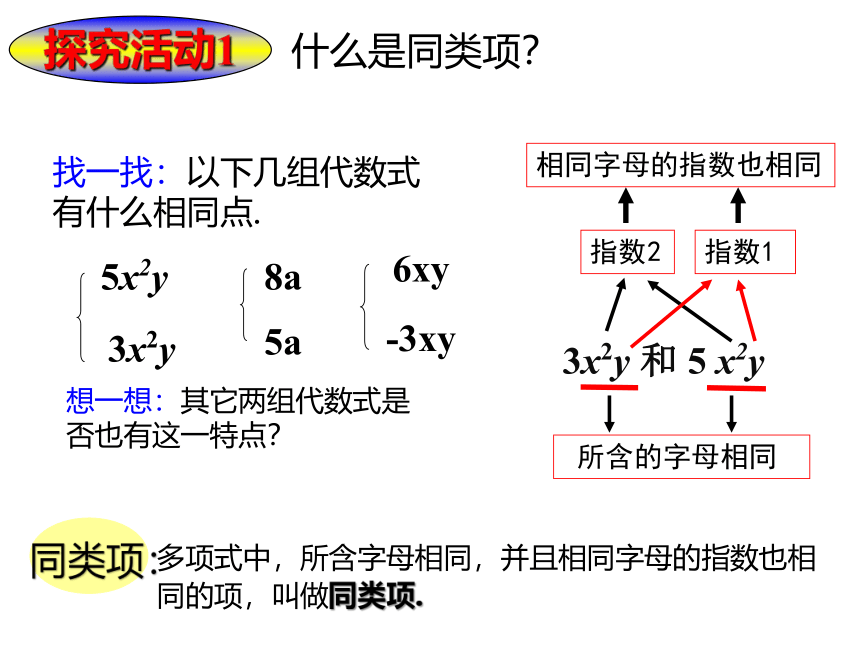
指数2
指数1
相同字母的指数也相同
所含的字母相同
3x2y 和 5 x2y
8a
5a
5x2y
3x2y
什么是同类项?
找一找:以下几组代数式有什么相同点.
6xy
-3xy
想一想:其它两组代数式是否也有这一特点?
多项式中,所含字母相同,并且相同字母的指数也相同的项,叫做同类项.
同类项:
探究活动1
★所含字母相同;
★相同字母的指数也相同.
★与字母顺序无关;
★与系数无关.
同类项的定义:所含字母相同,并且相同字母的指数也相同的项,叫做同类项.
★要注意:所有常数项都是同类项.
所有常数项都是同类项.
辨一辨:
下列各组中的两项是不是同类项?为什么?
(1)a3与b3 ( )
(3)3.5ab与0.5b a ( )
(4)-2 与 4 ( )
×
×
√
√
识别特征,深化概念
探究活动1
找同类项朋友
方法:
①现在老师有16张写有单项式的卡片分发给一些同学
②老师随意叫一位同学,这位同学站到前面来,并面对
全班同学高举自己的卡片。
③其他同学观察自己手中卡片和站起来这位同学卡片上的
单项式,若认为它们是同类项的,也请站到前面来。
④请其他同学做裁判,看看有没有找错朋友。
玩一玩:
找同类项的朋友
1号
-x2
3号
abc2
5号
-2yx2
10号
103c2ba
14号
-4x2y
2号
13号
- x2
11号
9 x2
15号
π
16号
-
6号
7号
abc2
8号
2×
9号
yx2
12号
3abc
4号
7x
玩一玩:
定义:把多项式中的同类项合并成一项叫做 合并同类项。
2
+
=
(2+1)
3
=
= 3y2
+
y2
2y2
=
y2
(2+1)
5x
2x
+
3x
=
=
(3+2) x
+
2
= 5
3
(3+2)
=
小明家里养了2头奶牛3只绵羊,
小红家里养了1头奶牛2只绵羊,
则他们两家共有多少奶牛和绵羊 ?
探究活动2
把同类项的系数相加,所得的结果作为系数,
字母及字母的指数不变。
x2y =
8
+
2
x2y
=
(10)
x2y
合并同类项法则:
合并下列同类项并归纳总结出合并同类项的方法:
+
-7m
4m =
(-3) m
=
(8+2) x2y
(-7+4)m
3ab2 - 4ab2 =
(简记为:一加,两不变)
系数
相加
系数
变了
字母和
字母指
数没变
合作学习
下列各题计算的结果对不对?如果不对,指出错在哪里?
( )
( )
( )
( )
×
×
√
×
错因:不是同类项不能合并
错因:系数合并对了,但是字母和字母的指数不变
错因:不是同类项不能合并
练一练
慧眼辨是非
既然要合并的是同类项,首先要做什么? 哪几项是同类项? 同类项不在相邻的位置,要怎么处理才便于合并?需要用什么方法进行变形? 没有同类项的项要怎么处理?
用不同的标记把同类项标出来!
解:4a2 + 2a + 3a - 8a2 - 2
- 8a2
= ( ) + ( )
+ 3a
2a
4a2
例、合并同类项:
找准、找全同类项.
结合同类项,连符号一起搬,没有同类项的照搬,括号之间是加号。
只把系数来相加,字母和字母的指数不变.
4a2 + 2a + 3a - 8a2 - 2
4
- 8
+ 3
2
= ( )a2 + ( ) a -2
=-4a2 + 5a -2
加法交换律加法结合律
- 2
通常我们把一个多项式的各项按照某个字母的指数从大到小(降幂)或者从小到大(升幂)的顺序排列,如-4a2 +5a-2也可以写成-2 +5a- 4a2
练一练
找出
结合
合并
灵活运用,延伸拓展
计算:
(1)x+7x-5x (2)-6ab+ba+8ab
(3)10y2-0.5y2 (4)3x2y-xy2 -2x2y+3xy2
练一练
同 类 项
合并同类项
定义
法则
(1)所含字母相同;
(2)相同字母的指数相同;
(1)系数相加
(2)字母连同它的指数不变。
一、概念
步骤
一找、二移、三并、
分类思想
(一加两不变)
两同两无关
对自己说,你有什么收获?
对老师说,你还有什么困惑?
几个常数项也是同类项
小结归纳:
2.选做题
教科书第65页练习第1、2题
1.必做题
已知单项式 和
都是 的同类项,则m +n=
3.预习课本65页例三
课后作业:
知识像一艘船,让它载着我们驶向理想的彼岸……
谢谢!
2.2整式的加减(1)
----合并同类项
1.理解同类项的概念
2.学会合并同类项
学习目标
如图:超市里新到的水果上架时怎样摆放呢?
情境导入:
8a
5a
5x2y
3x2y
6xy
-3xy
将下列单项式进行分类,并与同伴交流一下你为什么这么分类?
8a
3x2y
5x2y
-3xy
5a
6xy
探究新知:
指数2
指数1
相同字母的指数也相同
所含的字母相同
3x2y 和 5 x2y
8a
5a
5x2y
3x2y
什么是同类项?
找一找:以下几组代数式有什么相同点.
6xy
-3xy
想一想:其它两组代数式是否也有这一特点?
多项式中,所含字母相同,并且相同字母的指数也相同的项,叫做同类项.
同类项:
探究活动1
★所含字母相同;
★相同字母的指数也相同.
★与字母顺序无关;
★与系数无关.
同类项的定义:所含字母相同,并且相同字母的指数也相同的项,叫做同类项.
★要注意:所有常数项都是同类项.
所有常数项都是同类项.
辨一辨:
下列各组中的两项是不是同类项?为什么?
(1)a3与b3 ( )
(3)3.5ab与0.5b a ( )
(4)-2 与 4 ( )
×
×
√
√
识别特征,深化概念
探究活动1
找同类项朋友
方法:
①现在老师有16张写有单项式的卡片分发给一些同学
②老师随意叫一位同学,这位同学站到前面来,并面对
全班同学高举自己的卡片。
③其他同学观察自己手中卡片和站起来这位同学卡片上的
单项式,若认为它们是同类项的,也请站到前面来。
④请其他同学做裁判,看看有没有找错朋友。
玩一玩:
找同类项的朋友
1号
-x2
3号
abc2
5号
-2yx2
10号
103c2ba
14号
-4x2y
2号
13号
- x2
11号
9 x2
15号
π
16号
-
6号
7号
abc2
8号
2×
9号
yx2
12号
3abc
4号
7x
玩一玩:
定义:把多项式中的同类项合并成一项叫做 合并同类项。
2
+
=
(2+1)
3
=
= 3y2
+
y2
2y2
=
y2
(2+1)
5x
2x
+
3x
=
=
(3+2) x
+
2
= 5
3
(3+2)
=
小明家里养了2头奶牛3只绵羊,
小红家里养了1头奶牛2只绵羊,
则他们两家共有多少奶牛和绵羊 ?
探究活动2
把同类项的系数相加,所得的结果作为系数,
字母及字母的指数不变。
x2y =
8
+
2
x2y
=
(10)
x2y
合并同类项法则:
合并下列同类项并归纳总结出合并同类项的方法:
+
-7m
4m =
(-3) m
=
(8+2) x2y
(-7+4)m
3ab2 - 4ab2 =
(简记为:一加,两不变)
系数
相加
系数
变了
字母和
字母指
数没变
合作学习
下列各题计算的结果对不对?如果不对,指出错在哪里?
( )
( )
( )
( )
×
×
√
×
错因:不是同类项不能合并
错因:系数合并对了,但是字母和字母的指数不变
错因:不是同类项不能合并
练一练
慧眼辨是非
既然要合并的是同类项,首先要做什么? 哪几项是同类项? 同类项不在相邻的位置,要怎么处理才便于合并?需要用什么方法进行变形? 没有同类项的项要怎么处理?
用不同的标记把同类项标出来!
解:4a2 + 2a + 3a - 8a2 - 2
- 8a2
= ( ) + ( )
+ 3a
2a
4a2
例、合并同类项:
找准、找全同类项.
结合同类项,连符号一起搬,没有同类项的照搬,括号之间是加号。
只把系数来相加,字母和字母的指数不变.
4a2 + 2a + 3a - 8a2 - 2
4
- 8
+ 3
2
= ( )a2 + ( ) a -2
=-4a2 + 5a -2
加法交换律加法结合律
- 2
通常我们把一个多项式的各项按照某个字母的指数从大到小(降幂)或者从小到大(升幂)的顺序排列,如-4a2 +5a-2也可以写成-2 +5a- 4a2
练一练
找出
结合
合并
灵活运用,延伸拓展
计算:
(1)x+7x-5x (2)-6ab+ba+8ab
(3)10y2-0.5y2 (4)3x2y-xy2 -2x2y+3xy2
练一练
同 类 项
合并同类项
定义
法则
(1)所含字母相同;
(2)相同字母的指数相同;
(1)系数相加
(2)字母连同它的指数不变。
一、概念
步骤
一找、二移、三并、
分类思想
(一加两不变)
两同两无关
对自己说,你有什么收获?
对老师说,你还有什么困惑?
几个常数项也是同类项
小结归纳:
2.选做题
教科书第65页练习第1、2题
1.必做题
已知单项式 和
都是 的同类项,则m +n=
3.预习课本65页例三
课后作业:
知识像一艘船,让它载着我们驶向理想的彼岸……
谢谢!
