2021-2022学年湘教版九年级上学期数学期末练习试卷(word版含解析)
文档属性
| 名称 | 2021-2022学年湘教版九年级上学期数学期末练习试卷(word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 482.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-04 00:00:00 | ||
图片预览




文档简介
2021-2022学年湘教新版九年级上学期数学期末练习试卷
一.选择题(共10小题,满分40分,每小题4分)
1.把方程2x(x﹣1)=3x化成一元二次方程的一般形式,则二次项系数、一次项系数、常数项分别是( )
A.2,5,0 B.2,﹣5,0 C.2,5,1 D.2,3,0
2.已知反比例函数y=(k≠0)的图象在二、四象限,点(﹣1,y1),(2,y2),(3,y3)在此函数的图象上,则y1,y2,y3的大小关系是( )
A.y1>y2>y3 B.y3>y2>y1 C.y1>y3>y2 D.y2>y3>y1
3.不解方程,判别方程2x2﹣3x=3的根的情况( )
A.有两个相等的实数根 B.有两个不相等的实数根
C.有一个实数根 D.无实数根
4.点(﹣3,5)在反比例函数y=(k≠0)的图象上,则下列各点在该函数图象上的是( )
A.(5,﹣3) B.(﹣,3) C.(﹣5,﹣3) D.(,3)
5.某商场在销售一种日用品时发现,如果以单价20元销售,则每周可售出100件,若销售单价每提高0.5元,则每周销售量会相应减少2件.如果该商场这种日用品每周的销售额达到2024元.若设这种日用品的销售单价为x元,则根据题意所列方程正确的是( )
A.(20+x)(100﹣2x)=2024
B.(20+x)(100﹣)=2024
C.x[100﹣2(x﹣20)]=2024
D.x(100﹣×2)=2024
6.为调查某校1500名学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机抽取部分学生进行调查,并结合调查数据作出如图所示的扇形统计图.根据统计图提供的信息,可估算出该校喜爱体育节目的学生共有( )
A.1200名 B.450名 C.400名 D.300名
7.如图,在三角形纸片ABC中,AB=6,BC=8,AC=4.沿虚线剪下的涂色部分的三角形与△ABC相似的是( )
A. B.
C. D.
8.在下列网格中,小正方形的边长为1,点A、B、O都在格点上,则∠A的正弦值是( )
A. B. C. D.
9.矩形ABCD中,E为BC边中点,DG⊥AE交AE于点F,交AB于点G,连接CF,若tan∠AEB=3,AF=4,则线段CF的长为( )
A.4 B.5 C.6 D.
10.已知任意四边形ABCD中,对角线AC、BD交于点O,且AB=CD,若只增加下列条件中的一个:①AO=BO;②AC=BD;③;④∠OAD=∠OBC,一定能使∠BAC=∠CDB成立的可选条件是( )
A.② B.①② C.③④ D.②③④
二.填空题(共6小题,满分24分,每小题4分)
11.若一组数x1,x2,x3,…,xn的平均数为,方差为s2,则另一组数kx1,kx2,kx3,…,kxn的平均数和方差分别为 和 .
12.设m、n是方程x2+x﹣1001=0的两个实数根,则m2+2m+n的值为 .
13.在Rt△ABC中,∠C=90°,有两边长分别为3和4,则sinA的值为 .
14.《九章算术》中记载了一种测量古井水面以上部分深度的方法.如图所示,在井口A处立一根垂直于井口的木杆AB,从木杆的顶端B观察井水水岸D,视线BD与井口的直径AC交于点E,如果测得AB=1米,AC=1.6米,AE=0.4米,那么CD为 米.
15.在物理课中,同学们曾学过小孔成像:在较暗的屋子里,把一只点燃的蜡烛放在一块半透明的塑料薄膜前面,在它们之间放一块钻有小孔的纸板,由于光沿直线传播,塑料薄膜上就出现了蜡烛火焰倒立的像,这种现象就是小孔成像(如图1).如图2,如果火焰AB的高度是2cm,倒立的像A′B′的高度为5cm,
蜡烛火焰根B到小孔O的距离为4cm,则火焰根的像B′到O的距离是 cm.
16.如图,Rt△AOB的一条直角边OB在x轴上,双曲线y=经过斜边OA的中点C,与另一直角边交于点D.若S△OCD=9,则S△OBD的值为 .
三.解答题(共8小题,满分86分)
17.(10分)解方程:
(Ⅰ)(x+3)2=36;
(Ⅱ)3x2﹣1=6x.
18.(10分)计算:6sin45°﹣|1﹣|﹣×(π﹣2021)0﹣()﹣2.
19.(10分)如图,在第一象限内,点A,B在反比例函数(k>0)的图象上,AM⊥x轴于点M(3,0),△AOM的面积为3,BC∥AM交OA于点C,连结OB.
(1)求出k的值和直线OA的函数解析式.
(2)当点B的横坐标为2时,求△OBC的面积.
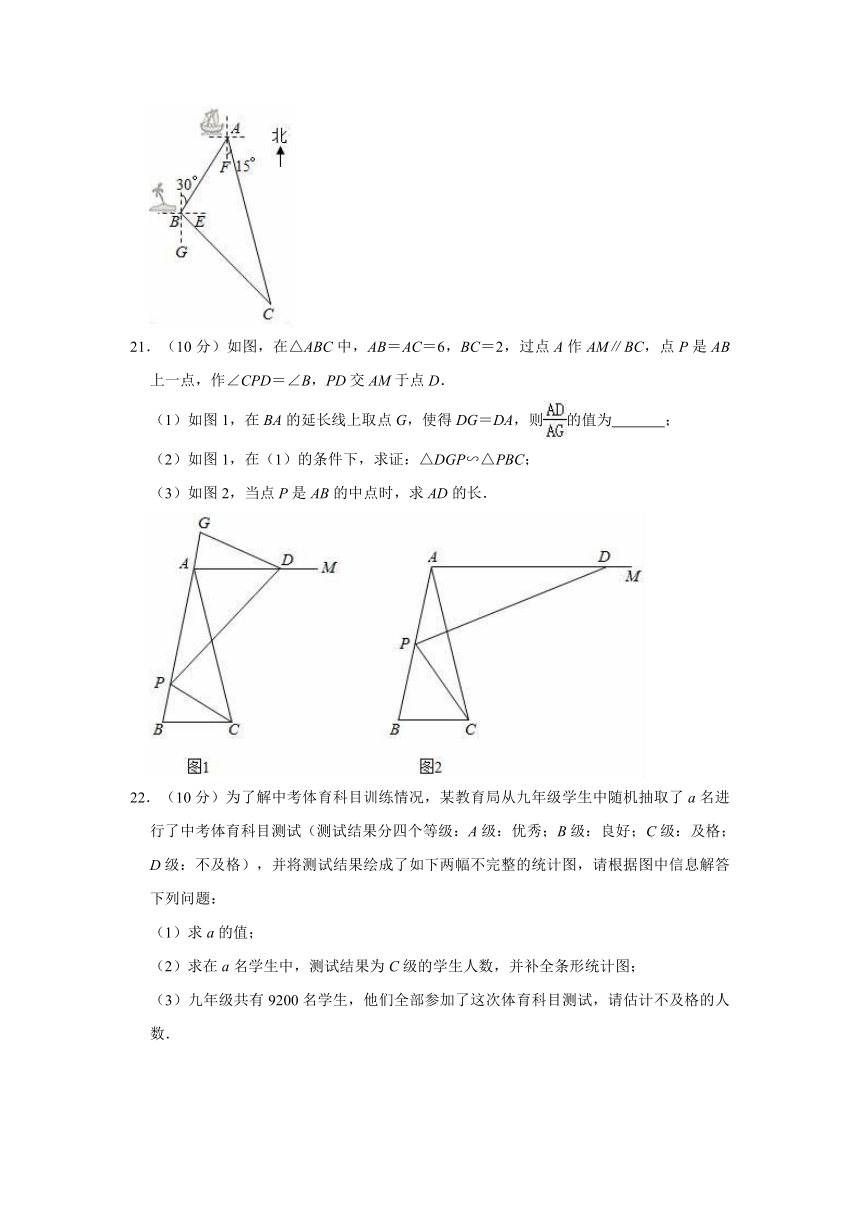
20.(10分)如图,一艘渔船位于小岛B的北偏东30°方向,距离小岛80nmile的点A处,它沿着点A的南偏东15°方向航行.
(1)渔船航行多远与小岛B的距离最近?(结果保留根号)
(2)渔船到达距离小岛B最近点后,按原航向继续航行40nmile到点C处时突然发生事故,渔船马上向小岛B上的救援队求救,问:救援队从B处出发沿着哪个方向航行到达事故地点航程最短,最短航程是多少?(结果保留根号)
21.(10分)如图,在△ABC中,AB=AC=6,BC=2,过点A作AM∥BC,点P是AB上一点,作∠CPD=∠B,PD交AM于点D.
(1)如图1,在BA的延长线上取点G,使得DG=DA,则的值为 ;
(2)如图1,在(1)的条件下,求证:△DGP∽△PBC;
(3)如图2,当点P是AB的中点时,求AD的长.
22.(10分)为了解中考体育科目训练情况,某教育局从九年级学生中随机抽取了a名进行了中考体育科目测试(测试结果分四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如下两幅不完整的统计图,请根据图中信息解答下列问题:
(1)求a的值;
(2)求在a名学生中,测试结果为C级的学生人数,并补全条形统计图;
(3)九年级共有9200名学生,他们全部参加了这次体育科目测试,请估计不及格的人数.
23.(12分)如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.
(1)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动,如果P,Q分别从A,B同时出发,经过几秒,点P,Q之间的距离为cm?
(2)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动,如果P,Q分别从A,B同时出发,经过几秒,使△PBQ的面积等于8cm2?
(3)若P点沿射线AB方向从A点出发以1cm/s的速度移动,点Q沿射线CB方向从C点出发以2cm/s的速度移动,P,Q同时出发,几秒后,△PBQ的面积为1cm2?
24.(14分)如图,在矩形ABCD中,E是BC的中点,DF⊥AE,垂足为F.
(1)求证△ADF∽△EAB;
(2)若AB=12,BC=10,求DF的长.
参考答案与试题解析
一.选择题(共10小题,满分40分,每小题4分)
1.解:方程2x(x﹣1)=3x,
整理得:2x2﹣5x=0,
则二次项系数为2,一次项系数为﹣5,常数项为0.
故选:B.
2.解:∵图象在二、四象限,
∴k<0,
∴在每个象限内,y随x值的增大而增大,
∴当x=﹣1时,y1>0,
∵2<3,
∴y2<y3<0,
∴y2<y3<y1,即y1>y3>y2.
故选:C.
3.解:方程整理得2x2﹣3x﹣3=0,
∵Δ=(﹣3)2﹣4×2×(﹣3)=18+24>0,
∴方程有两个不相等的实数根.
故选:B.
4.解:∵点(﹣3,5)在反比例函数y=(k≠0)的图象上,
∴k=﹣3×5=﹣15,
A、∵5×(﹣3)=﹣15,∴此点在反比例函数的图象上,故本选项符合题意;
B、∵﹣×3=﹣≠﹣15,∴此点不在反比例函数的图象上,故本选项不合题意;
C、∵﹣5×(﹣3)=15≠﹣15,∴此点不在反比例函数的图象上,故本选项不合题意;
D、∵×3=≠﹣15,∴此点不在反比例函数的图象上,故本选项不合题意.
故选:A.
5.解:由题意可得,
x(100﹣×2)=2024,
故选:D.
6.解;∵喜爱体育节目的学生占1﹣10%﹣5%﹣35%﹣30%=20%,该校共1500名学生,
∴该校喜爱体育节目的学生共有1500×20%=300(名),
故选:D.
7.解:在三角形纸片ABC中,AB=6,BC=8,AC=4.
A.∵==,对应边==,≠,
故沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
B.∵=,对应边==,≠,
故沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
C.∵=,对应边=,即:=,∠C=∠C,
故沿虚线剪下的涂色部分的三角形与△ABC相似,故此选项正确;
D.∵==,
=,≠,
故沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
故选:C.
8.解:由题意得,OC=2,AC=4,
由勾股定理得,AO==2,
∴sinA==,
故选:A.
9.解:延长AE交DC的延长线于点M,
∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,
∴∠B=∠ECM,
∵E为BC的中点,
∴BE=CE,
在△ABE和△MCE中,
,
∴△ABE≌△MCE(ASA),
∴AB=CM,
∴DC=CM,
∵DG⊥AE,
∴CF=DM=DC,
∵AD∥BC,
∴∠AEB=∠FAD,
∴tan∠AEB=tan∠FAD=3,
∵AF=4,
∴DF=12,
∴AD===4,
∴BE=2,
∴AB=3BE=6,
∴CF=CD=6.
故选:C.
10.解:①由AO=BO,只能得出△AOB为等腰三角形,不一定能使∠BAC=∠CDB成立;
②AC=BD,再由AB=CD,BC=BC,可证△ABC≌△DCB,则∠BAC=∠CDB,能使∠BAC=∠CDB成立;
③,可证AD∥BC,可再由AB=CD推出ABCD等腰梯形,一定能使∠BAC=∠CDB成立;
④∵∠OAD=∠OBC,∴A,B,C,D四点共圆,一定能使∠BAC=∠CDB成立.
故选:D.
二.填空题(共6小题,满分24分,每小题4分)
11.解:∵x1,x2,x3,…,xn的平均数为,方差为s2,
∴kx1,kx2,kx3,…,kxn的平均数为k,方差为k2s2,
故答案为:k,k2s2.
12.解:∵m、n是方程x2+x﹣1001=0的两个实数根,
∴m+n=﹣1,
并且m2+m﹣1001=0,
∴m2+m=1001,
∴m2+2m+n=m2+m+m+n=1001﹣1=1000.
故答案为:1000.
13.解:根据题意画图如下:
如图(1)当BC=4,AC=3时,AB=5,则sinA的值为;
如图(2)当BC=3,AC=4时,AB=5,则sinA的值为;
如图(3)当AB=4,BC=3时,则sinA的值为;
如图(4)当AB=4,AC=3时,BC=,则sinA的值为;
则sinA的值为或或或.
故答案为:或或或.
14.解:由题意知:AB∥CD,
则∠BAE=∠C,∠B=∠CDE,
∴△ABE∽△CDE,
∴,
∴,
∴CD=3米,
故答案为:3.
15.解:如图,
∵AB∥A′B′,
∴△ABO∽△A′B′O,
则=,即=,
解得:OB′=10,
故答案为:10.
16.解:如图,过C点作CE⊥x轴,垂足为E.
∵Rt△OAB中,∠OBA=90°,
∴CE∥AB,
∵C为Rt△OAB斜边OA的中点C,
∴CE为Rt△OAB的中位线,
∵△OEC∽△OBA,
∴=.
∵双曲线的解析式是y=,即xy=k
∴S△BOD=S△COE=|k|,
∴S△AOB=4S△COE=2|k|,
由S△AOB﹣S△BOD=S△AOD=2S△DOC=18,得2k﹣k=18,
k=12,
S△BOD=S△COE=k=6,
故答案为:6.
三.解答题(共8小题,满分86分)
17.解:(Ⅰ)(x+3)2=36,
x+3=±6,
x+3=6,
x1=3,
x+3=﹣6,
x2=﹣9,
∴x1=3,x2=﹣9,
(Ⅱ)3x2﹣1=6x,
3x2﹣6x﹣1=0,
a=3,b=﹣6,c=﹣1,
Δ=b2﹣4ac=(﹣6)2﹣4×3×(﹣1)=48>0,
∴方程有两个不相等的实数根,
∴x=,
∴x1=,x2=.
18.解:原式=6×﹣(﹣1)﹣2×1﹣4
=3﹣+1﹣2﹣4
=﹣3.
19.解:(1)∵△AOM的面积为3,设A(x,y),
∴=3,
则xy=6=k,
故A坐标为(3,2),
设直线OA的解析式为y=mx,代入点A(3,2),
得2=3m,m=,
故k=6,直线OA的解析式为y=x;
(2)延长BC交x轴于点N,
设B坐标为(2,m),
∴2m=6,m=3,
把x=2代入y=x中,得y=,
即C点纵坐标为,
∴BC=3﹣=,
又ON=2,
∴S△OBC===.
20.解:(1)过点B作BM⊥AC于点M,如图所示:
由题意,知∠BAM=45°,则∠ABM=45°.
在Rt△ABM中,∠BAM=45°,AB=80nmile,
∴△ABM是等腰直角三角形,
∴BM=AM=AB=40(nmile)
答:渔船航行40nmile与小岛B的距离最近.
(2)∵BM=40nmile,MC=40nmile,
∴,
∴∠MBC=60°,
∴∠CBG=180°﹣60°﹣45°﹣30°=45°,
在Rt△BCM中,∠MBC=60°,
∴∠BCM=30°,
∴BC=2BM=80(nmile),
答:救援队从B处出发沿着点B的南偏东45°方向航行到达事故地点航程最短,最短航程是80nmile.
21.解:(1)∵AM∥BC,
∴∠GAD=∠B,
∵AB=AC,
∴∠B=∠ACB,
∵AD=DG,
∴∠GAD=∠G,
∴∠G=∠ACB,
∴△ADG∽△ABC,
∴,
∵AB=6,BC=2,
∴,
∴;
故答案为:3.
(2)证明:∵∠APC=∠GPD+∠DPC,∠APC=∠B+∠BCP,
又∠CPD=∠B,
∴∠GPD=∠BCP,
又AD=DG,
∴∠G=∠GAD,
∵AM∥BC,
∴∠GAD=∠B,
∴∠G=∠B,
∴△DGP∽△PBC;
(3)在BA的延长线上取点G,使得DA=DG.
由(1)知,
∵点P是AB的中点,
∴AP=BP=3,
设AD=x,则DG=x,AG=,PG=3+,
由(2)得△DGP∽△PBC,
∴,
∴,
解得x=9,
∴AD=9.
22.解:(1)a=12÷30%=40;
(2)C级的人数为40×35%=14(名),
;
(3)9200×=1840(名).
答:不及格的人数是1840名.
23.解:(1)设经过x秒,点P,Q之间的距离为cm,
则AP=x(cm),QB=2x(cm),
∵AB=6cm,BC=8cm
∴PB=(6﹣x)(cm),
∵在△ABC中,∠B=90°
∴由勾股定理得:(6﹣x)2+(2x)2=6
化简得:5x2﹣12x+30=0
∵△=(﹣12)2﹣4×5×30=144﹣600<0
∴点P,Q之间的距离不可能为cm.
(2)设经过x秒,使△PBQ的面积等于8cm2,由题意得:
(6﹣x) 2x=8
解得:x1=2,x2=4
检验发现x1,x2均符合题意
∴经过2秒或4秒,△PBQ的面积等于8cm2.
(3)①点P在线段AB上,点Q在线段CB上
设经过m秒,0<m≤4,依题意有
(6﹣m)(8﹣2m)=1
∴m2﹣10m+23=0
解得;m1=5+(舍),m2=5﹣
∴m=5﹣符合题意;
②点P在线段AB上,点Q在射线CB上
设经过n秒,4<n≤6,依题意有
(6﹣n)(2n﹣8)=1
∴n2﹣10n+25=0
解得n1=n2=5
∴n=5符合题意;
③点P在射线AB上,点Q在射线CB上
设经过k秒,k>6,依题意有
(k﹣6)(2k﹣8)=1
解得k1=5+,k2=5﹣(舍)
∴k=5+符合题意;
∴经过(5﹣)秒,5秒,(5+)秒后,△PBQ的面积为1cm2.
24.(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,∠B=90°,
∴∠DAF=∠AEB,
∵DF⊥AE,
∴∠AFD=90°=∠B,
∴△ADF∽△EAB;
(2)解:∵BC=AD=10,E是BC边的中点,
∴BE=5,
∴AE===13,
由(1)得:△ADF∽△EAB,
∴=,
即=,
解得:DF=.
一.选择题(共10小题,满分40分,每小题4分)
1.把方程2x(x﹣1)=3x化成一元二次方程的一般形式,则二次项系数、一次项系数、常数项分别是( )
A.2,5,0 B.2,﹣5,0 C.2,5,1 D.2,3,0
2.已知反比例函数y=(k≠0)的图象在二、四象限,点(﹣1,y1),(2,y2),(3,y3)在此函数的图象上,则y1,y2,y3的大小关系是( )
A.y1>y2>y3 B.y3>y2>y1 C.y1>y3>y2 D.y2>y3>y1
3.不解方程,判别方程2x2﹣3x=3的根的情况( )
A.有两个相等的实数根 B.有两个不相等的实数根
C.有一个实数根 D.无实数根
4.点(﹣3,5)在反比例函数y=(k≠0)的图象上,则下列各点在该函数图象上的是( )
A.(5,﹣3) B.(﹣,3) C.(﹣5,﹣3) D.(,3)
5.某商场在销售一种日用品时发现,如果以单价20元销售,则每周可售出100件,若销售单价每提高0.5元,则每周销售量会相应减少2件.如果该商场这种日用品每周的销售额达到2024元.若设这种日用品的销售单价为x元,则根据题意所列方程正确的是( )
A.(20+x)(100﹣2x)=2024
B.(20+x)(100﹣)=2024
C.x[100﹣2(x﹣20)]=2024
D.x(100﹣×2)=2024
6.为调查某校1500名学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机抽取部分学生进行调查,并结合调查数据作出如图所示的扇形统计图.根据统计图提供的信息,可估算出该校喜爱体育节目的学生共有( )
A.1200名 B.450名 C.400名 D.300名
7.如图,在三角形纸片ABC中,AB=6,BC=8,AC=4.沿虚线剪下的涂色部分的三角形与△ABC相似的是( )
A. B.
C. D.
8.在下列网格中,小正方形的边长为1,点A、B、O都在格点上,则∠A的正弦值是( )
A. B. C. D.
9.矩形ABCD中,E为BC边中点,DG⊥AE交AE于点F,交AB于点G,连接CF,若tan∠AEB=3,AF=4,则线段CF的长为( )
A.4 B.5 C.6 D.
10.已知任意四边形ABCD中,对角线AC、BD交于点O,且AB=CD,若只增加下列条件中的一个:①AO=BO;②AC=BD;③;④∠OAD=∠OBC,一定能使∠BAC=∠CDB成立的可选条件是( )
A.② B.①② C.③④ D.②③④
二.填空题(共6小题,满分24分,每小题4分)
11.若一组数x1,x2,x3,…,xn的平均数为,方差为s2,则另一组数kx1,kx2,kx3,…,kxn的平均数和方差分别为 和 .
12.设m、n是方程x2+x﹣1001=0的两个实数根,则m2+2m+n的值为 .
13.在Rt△ABC中,∠C=90°,有两边长分别为3和4,则sinA的值为 .
14.《九章算术》中记载了一种测量古井水面以上部分深度的方法.如图所示,在井口A处立一根垂直于井口的木杆AB,从木杆的顶端B观察井水水岸D,视线BD与井口的直径AC交于点E,如果测得AB=1米,AC=1.6米,AE=0.4米,那么CD为 米.
15.在物理课中,同学们曾学过小孔成像:在较暗的屋子里,把一只点燃的蜡烛放在一块半透明的塑料薄膜前面,在它们之间放一块钻有小孔的纸板,由于光沿直线传播,塑料薄膜上就出现了蜡烛火焰倒立的像,这种现象就是小孔成像(如图1).如图2,如果火焰AB的高度是2cm,倒立的像A′B′的高度为5cm,
蜡烛火焰根B到小孔O的距离为4cm,则火焰根的像B′到O的距离是 cm.
16.如图,Rt△AOB的一条直角边OB在x轴上,双曲线y=经过斜边OA的中点C,与另一直角边交于点D.若S△OCD=9,则S△OBD的值为 .
三.解答题(共8小题,满分86分)
17.(10分)解方程:
(Ⅰ)(x+3)2=36;
(Ⅱ)3x2﹣1=6x.
18.(10分)计算:6sin45°﹣|1﹣|﹣×(π﹣2021)0﹣()﹣2.
19.(10分)如图,在第一象限内,点A,B在反比例函数(k>0)的图象上,AM⊥x轴于点M(3,0),△AOM的面积为3,BC∥AM交OA于点C,连结OB.
(1)求出k的值和直线OA的函数解析式.
(2)当点B的横坐标为2时,求△OBC的面积.
20.(10分)如图,一艘渔船位于小岛B的北偏东30°方向,距离小岛80nmile的点A处,它沿着点A的南偏东15°方向航行.
(1)渔船航行多远与小岛B的距离最近?(结果保留根号)
(2)渔船到达距离小岛B最近点后,按原航向继续航行40nmile到点C处时突然发生事故,渔船马上向小岛B上的救援队求救,问:救援队从B处出发沿着哪个方向航行到达事故地点航程最短,最短航程是多少?(结果保留根号)
21.(10分)如图,在△ABC中,AB=AC=6,BC=2,过点A作AM∥BC,点P是AB上一点,作∠CPD=∠B,PD交AM于点D.
(1)如图1,在BA的延长线上取点G,使得DG=DA,则的值为 ;
(2)如图1,在(1)的条件下,求证:△DGP∽△PBC;
(3)如图2,当点P是AB的中点时,求AD的长.
22.(10分)为了解中考体育科目训练情况,某教育局从九年级学生中随机抽取了a名进行了中考体育科目测试(测试结果分四个等级:A级:优秀;B级:良好;C级:及格;D级:不及格),并将测试结果绘成了如下两幅不完整的统计图,请根据图中信息解答下列问题:
(1)求a的值;
(2)求在a名学生中,测试结果为C级的学生人数,并补全条形统计图;
(3)九年级共有9200名学生,他们全部参加了这次体育科目测试,请估计不及格的人数.
23.(12分)如图所示,△ABC中,∠B=90°,AB=6cm,BC=8cm.
(1)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动,如果P,Q分别从A,B同时出发,经过几秒,点P,Q之间的距离为cm?
(2)点P从点A开始沿AB边向B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动,如果P,Q分别从A,B同时出发,经过几秒,使△PBQ的面积等于8cm2?
(3)若P点沿射线AB方向从A点出发以1cm/s的速度移动,点Q沿射线CB方向从C点出发以2cm/s的速度移动,P,Q同时出发,几秒后,△PBQ的面积为1cm2?
24.(14分)如图,在矩形ABCD中,E是BC的中点,DF⊥AE,垂足为F.
(1)求证△ADF∽△EAB;
(2)若AB=12,BC=10,求DF的长.
参考答案与试题解析
一.选择题(共10小题,满分40分,每小题4分)
1.解:方程2x(x﹣1)=3x,
整理得:2x2﹣5x=0,
则二次项系数为2,一次项系数为﹣5,常数项为0.
故选:B.
2.解:∵图象在二、四象限,
∴k<0,
∴在每个象限内,y随x值的增大而增大,
∴当x=﹣1时,y1>0,
∵2<3,
∴y2<y3<0,
∴y2<y3<y1,即y1>y3>y2.
故选:C.
3.解:方程整理得2x2﹣3x﹣3=0,
∵Δ=(﹣3)2﹣4×2×(﹣3)=18+24>0,
∴方程有两个不相等的实数根.
故选:B.
4.解:∵点(﹣3,5)在反比例函数y=(k≠0)的图象上,
∴k=﹣3×5=﹣15,
A、∵5×(﹣3)=﹣15,∴此点在反比例函数的图象上,故本选项符合题意;
B、∵﹣×3=﹣≠﹣15,∴此点不在反比例函数的图象上,故本选项不合题意;
C、∵﹣5×(﹣3)=15≠﹣15,∴此点不在反比例函数的图象上,故本选项不合题意;
D、∵×3=≠﹣15,∴此点不在反比例函数的图象上,故本选项不合题意.
故选:A.
5.解:由题意可得,
x(100﹣×2)=2024,
故选:D.
6.解;∵喜爱体育节目的学生占1﹣10%﹣5%﹣35%﹣30%=20%,该校共1500名学生,
∴该校喜爱体育节目的学生共有1500×20%=300(名),
故选:D.
7.解:在三角形纸片ABC中,AB=6,BC=8,AC=4.
A.∵==,对应边==,≠,
故沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
B.∵=,对应边==,≠,
故沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
C.∵=,对应边=,即:=,∠C=∠C,
故沿虚线剪下的涂色部分的三角形与△ABC相似,故此选项正确;
D.∵==,
=,≠,
故沿虚线剪下的涂色部分的三角形与△ABC不相似,故此选项错误;
故选:C.
8.解:由题意得,OC=2,AC=4,
由勾股定理得,AO==2,
∴sinA==,
故选:A.
9.解:延长AE交DC的延长线于点M,
∵四边形ABCD是矩形,
∴AB=CD,AB∥CD,
∴∠B=∠ECM,
∵E为BC的中点,
∴BE=CE,
在△ABE和△MCE中,
,
∴△ABE≌△MCE(ASA),
∴AB=CM,
∴DC=CM,
∵DG⊥AE,
∴CF=DM=DC,
∵AD∥BC,
∴∠AEB=∠FAD,
∴tan∠AEB=tan∠FAD=3,
∵AF=4,
∴DF=12,
∴AD===4,
∴BE=2,
∴AB=3BE=6,
∴CF=CD=6.
故选:C.
10.解:①由AO=BO,只能得出△AOB为等腰三角形,不一定能使∠BAC=∠CDB成立;
②AC=BD,再由AB=CD,BC=BC,可证△ABC≌△DCB,则∠BAC=∠CDB,能使∠BAC=∠CDB成立;
③,可证AD∥BC,可再由AB=CD推出ABCD等腰梯形,一定能使∠BAC=∠CDB成立;
④∵∠OAD=∠OBC,∴A,B,C,D四点共圆,一定能使∠BAC=∠CDB成立.
故选:D.
二.填空题(共6小题,满分24分,每小题4分)
11.解:∵x1,x2,x3,…,xn的平均数为,方差为s2,
∴kx1,kx2,kx3,…,kxn的平均数为k,方差为k2s2,
故答案为:k,k2s2.
12.解:∵m、n是方程x2+x﹣1001=0的两个实数根,
∴m+n=﹣1,
并且m2+m﹣1001=0,
∴m2+m=1001,
∴m2+2m+n=m2+m+m+n=1001﹣1=1000.
故答案为:1000.
13.解:根据题意画图如下:
如图(1)当BC=4,AC=3时,AB=5,则sinA的值为;
如图(2)当BC=3,AC=4时,AB=5,则sinA的值为;
如图(3)当AB=4,BC=3时,则sinA的值为;
如图(4)当AB=4,AC=3时,BC=,则sinA的值为;
则sinA的值为或或或.
故答案为:或或或.
14.解:由题意知:AB∥CD,
则∠BAE=∠C,∠B=∠CDE,
∴△ABE∽△CDE,
∴,
∴,
∴CD=3米,
故答案为:3.
15.解:如图,
∵AB∥A′B′,
∴△ABO∽△A′B′O,
则=,即=,
解得:OB′=10,
故答案为:10.
16.解:如图,过C点作CE⊥x轴,垂足为E.
∵Rt△OAB中,∠OBA=90°,
∴CE∥AB,
∵C为Rt△OAB斜边OA的中点C,
∴CE为Rt△OAB的中位线,
∵△OEC∽△OBA,
∴=.
∵双曲线的解析式是y=,即xy=k
∴S△BOD=S△COE=|k|,
∴S△AOB=4S△COE=2|k|,
由S△AOB﹣S△BOD=S△AOD=2S△DOC=18,得2k﹣k=18,
k=12,
S△BOD=S△COE=k=6,
故答案为:6.
三.解答题(共8小题,满分86分)
17.解:(Ⅰ)(x+3)2=36,
x+3=±6,
x+3=6,
x1=3,
x+3=﹣6,
x2=﹣9,
∴x1=3,x2=﹣9,
(Ⅱ)3x2﹣1=6x,
3x2﹣6x﹣1=0,
a=3,b=﹣6,c=﹣1,
Δ=b2﹣4ac=(﹣6)2﹣4×3×(﹣1)=48>0,
∴方程有两个不相等的实数根,
∴x=,
∴x1=,x2=.
18.解:原式=6×﹣(﹣1)﹣2×1﹣4
=3﹣+1﹣2﹣4
=﹣3.
19.解:(1)∵△AOM的面积为3,设A(x,y),
∴=3,
则xy=6=k,
故A坐标为(3,2),
设直线OA的解析式为y=mx,代入点A(3,2),
得2=3m,m=,
故k=6,直线OA的解析式为y=x;
(2)延长BC交x轴于点N,
设B坐标为(2,m),
∴2m=6,m=3,
把x=2代入y=x中,得y=,
即C点纵坐标为,
∴BC=3﹣=,
又ON=2,
∴S△OBC===.
20.解:(1)过点B作BM⊥AC于点M,如图所示:
由题意,知∠BAM=45°,则∠ABM=45°.
在Rt△ABM中,∠BAM=45°,AB=80nmile,
∴△ABM是等腰直角三角形,
∴BM=AM=AB=40(nmile)
答:渔船航行40nmile与小岛B的距离最近.
(2)∵BM=40nmile,MC=40nmile,
∴,
∴∠MBC=60°,
∴∠CBG=180°﹣60°﹣45°﹣30°=45°,
在Rt△BCM中,∠MBC=60°,
∴∠BCM=30°,
∴BC=2BM=80(nmile),
答:救援队从B处出发沿着点B的南偏东45°方向航行到达事故地点航程最短,最短航程是80nmile.
21.解:(1)∵AM∥BC,
∴∠GAD=∠B,
∵AB=AC,
∴∠B=∠ACB,
∵AD=DG,
∴∠GAD=∠G,
∴∠G=∠ACB,
∴△ADG∽△ABC,
∴,
∵AB=6,BC=2,
∴,
∴;
故答案为:3.
(2)证明:∵∠APC=∠GPD+∠DPC,∠APC=∠B+∠BCP,
又∠CPD=∠B,
∴∠GPD=∠BCP,
又AD=DG,
∴∠G=∠GAD,
∵AM∥BC,
∴∠GAD=∠B,
∴∠G=∠B,
∴△DGP∽△PBC;
(3)在BA的延长线上取点G,使得DA=DG.
由(1)知,
∵点P是AB的中点,
∴AP=BP=3,
设AD=x,则DG=x,AG=,PG=3+,
由(2)得△DGP∽△PBC,
∴,
∴,
解得x=9,
∴AD=9.
22.解:(1)a=12÷30%=40;
(2)C级的人数为40×35%=14(名),
;
(3)9200×=1840(名).
答:不及格的人数是1840名.
23.解:(1)设经过x秒,点P,Q之间的距离为cm,
则AP=x(cm),QB=2x(cm),
∵AB=6cm,BC=8cm
∴PB=(6﹣x)(cm),
∵在△ABC中,∠B=90°
∴由勾股定理得:(6﹣x)2+(2x)2=6
化简得:5x2﹣12x+30=0
∵△=(﹣12)2﹣4×5×30=144﹣600<0
∴点P,Q之间的距离不可能为cm.
(2)设经过x秒,使△PBQ的面积等于8cm2,由题意得:
(6﹣x) 2x=8
解得:x1=2,x2=4
检验发现x1,x2均符合题意
∴经过2秒或4秒,△PBQ的面积等于8cm2.
(3)①点P在线段AB上,点Q在线段CB上
设经过m秒,0<m≤4,依题意有
(6﹣m)(8﹣2m)=1
∴m2﹣10m+23=0
解得;m1=5+(舍),m2=5﹣
∴m=5﹣符合题意;
②点P在线段AB上,点Q在射线CB上
设经过n秒,4<n≤6,依题意有
(6﹣n)(2n﹣8)=1
∴n2﹣10n+25=0
解得n1=n2=5
∴n=5符合题意;
③点P在射线AB上,点Q在射线CB上
设经过k秒,k>6,依题意有
(k﹣6)(2k﹣8)=1
解得k1=5+,k2=5﹣(舍)
∴k=5+符合题意;
∴经过(5﹣)秒,5秒,(5+)秒后,△PBQ的面积为1cm2.
24.(1)证明:∵四边形ABCD是矩形,
∴AD∥BC,∠B=90°,
∴∠DAF=∠AEB,
∵DF⊥AE,
∴∠AFD=90°=∠B,
∴△ADF∽△EAB;
(2)解:∵BC=AD=10,E是BC边的中点,
∴BE=5,
∴AE===13,
由(1)得:△ADF∽△EAB,
∴=,
即=,
解得:DF=.
同课章节目录
