2021-2022学年沪科版八年级数学下册第18章勾股定理随堂练习(Word版,附答案)
文档属性
| 名称 | 2021-2022学年沪科版八年级数学下册第18章勾股定理随堂练习(Word版,附答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 131.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-04 00:00:00 | ||
图片预览

文档简介
第18章勾股定理
一、选择题(共15题)
下列四组线段中,可以构成直角三角形的是
A. ,, B. ,, C. ,, D. ,,
设三角形的三边长分别等于下列各组数,能构成直角三角形的是
A. ,, B. ,, C. ,, D. ,,
如图,已知在 中,,,分别以 , 为直径作半圆,面积分别记为 ,,则 的值等于
A. B. C. D.
如图,在 中,,,边 在数轴上.点 表示的数为 ,点 表示的数为 ,以 为圆心, 的长为半径画弧交数轴负半轴于点 ,则 表示的数是
A. B. C. D.
如图,两个较大正方形的面积分别为 ,,则字母 所代表的正方形的边长为
A. B. C. D.
以下列各组数据为三角形的三边,能构成直角三角形的是
A. ,, B. ,,
C. ,, D. ,,
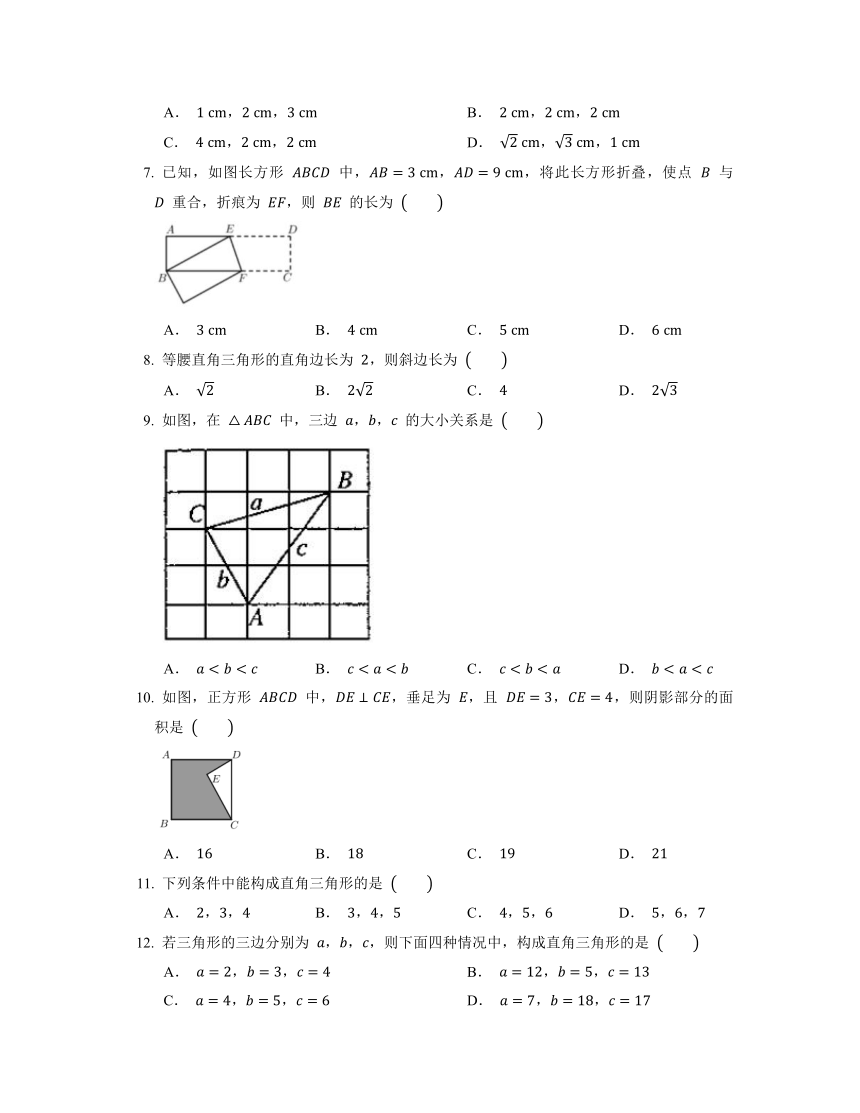
已知,如图长方形 中,,,将此长方形折叠,使点 与 重合,折痕为 ,则 的长为
A. B. C. D.
等腰直角三角形的直角边长为 ,则斜边长为
A. B. C. D.
如图,在 中,三边 ,, 的大小关系是
A. B. C. D.
如图,正方形 中,,垂足为 ,且 ,,则阴影部分的面积是
A. B. C. D.
下列条件中能构成直角三角形的是
A. ,, B. ,, C. ,, D. ,,
若三角形的三边分别为 ,,,则下面四种情况中,构成直角三角形的是
A. ,, B. ,,
C. ,, D. ,,
在 中,,,,则 的值
A. B. C. D.
下列各组数,可以作为直角三角形的三边长的是
A. ,, B. ,, C. ,, D. ,,
如果下列各组数是三角形的三边,那么不能组成直角三角形的一组数是
A. ,, B. ,, C. ,, D. ,,
二、填空题(共4题)
若一个三角形的三边长分别为 ,,,则这个三角形的面积为 .
已知 ,, 是 中 ,, 的对边,下列说法:
①若 ,则 ;②若 ,则 ;③若 则 ;④总有 .其中正确的有 (填序号).
若一个长方形的长与宽分别为 和 ,则它的对角线长为 .
已知 的三边长为 ,,,满足 ,,,则此三角形是 三角形.
三、解答题(共4题)
如图,在 的正方形网格中,每个小正方形的边长为 , 的顶点 ,, 均在格点上.
(1)求 的面积.
(2)试判断 的形状,并说明理由.
如图,在四边形 中,,,,.分别以点 , 为圆心,大于 的长为半径作弧,两弧交于点 ,作射线 交 于点 ,交 于点 ,点 是 的中点.
(1)求证:;
(2)求 的长.
如图,要修建一个育苗棚,棚高 ,棚宽 ,棚的长为 ,现要在棚顶上覆盖塑料薄膜,试求需要多少平方米塑料薄膜?
如图,在 的正方形网格中,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
(1) 在图①中,画一个直角三角形,使它的三边长都是有理数;
(2) 在图②中,画一个直角三角形,使它的一边长是有理数,另外两边长是无理数;
(3) 在图③中,画一个直角三角形,使它的三边长都是无理数.
答案
1. C
2. A
3. A
4. C
5. C
6. D
7. C
8. B
9. D
10. C
11. B
12. B
13. A
14. B
15. B
16.
17. ①②③
18.
19. 直角
20. (1) 所以 的面积为 .
(2) 判断 是直角三角形.理由如下:因为 ,,,所以 .所以 是直角三角形.
21. (1) , , ,, , .
(2) 连接 ,易证 垂直平分 , ,由()知 , ,.在 中, , , , .
22. 平方米.
23. (1) 如答图①, 即为所求.(2) 如答图②, 即为所求.(答案不唯一)
(3) 如答图③, 即为所求.(答案不唯一)
一、选择题(共15题)
下列四组线段中,可以构成直角三角形的是
A. ,, B. ,, C. ,, D. ,,
设三角形的三边长分别等于下列各组数,能构成直角三角形的是
A. ,, B. ,, C. ,, D. ,,
如图,已知在 中,,,分别以 , 为直径作半圆,面积分别记为 ,,则 的值等于
A. B. C. D.
如图,在 中,,,边 在数轴上.点 表示的数为 ,点 表示的数为 ,以 为圆心, 的长为半径画弧交数轴负半轴于点 ,则 表示的数是
A. B. C. D.
如图,两个较大正方形的面积分别为 ,,则字母 所代表的正方形的边长为
A. B. C. D.
以下列各组数据为三角形的三边,能构成直角三角形的是
A. ,, B. ,,
C. ,, D. ,,
已知,如图长方形 中,,,将此长方形折叠,使点 与 重合,折痕为 ,则 的长为
A. B. C. D.
等腰直角三角形的直角边长为 ,则斜边长为
A. B. C. D.
如图,在 中,三边 ,, 的大小关系是
A. B. C. D.
如图,正方形 中,,垂足为 ,且 ,,则阴影部分的面积是
A. B. C. D.
下列条件中能构成直角三角形的是
A. ,, B. ,, C. ,, D. ,,
若三角形的三边分别为 ,,,则下面四种情况中,构成直角三角形的是
A. ,, B. ,,
C. ,, D. ,,
在 中,,,,则 的值
A. B. C. D.
下列各组数,可以作为直角三角形的三边长的是
A. ,, B. ,, C. ,, D. ,,
如果下列各组数是三角形的三边,那么不能组成直角三角形的一组数是
A. ,, B. ,, C. ,, D. ,,
二、填空题(共4题)
若一个三角形的三边长分别为 ,,,则这个三角形的面积为 .
已知 ,, 是 中 ,, 的对边,下列说法:
①若 ,则 ;②若 ,则 ;③若 则 ;④总有 .其中正确的有 (填序号).
若一个长方形的长与宽分别为 和 ,则它的对角线长为 .
已知 的三边长为 ,,,满足 ,,,则此三角形是 三角形.
三、解答题(共4题)
如图,在 的正方形网格中,每个小正方形的边长为 , 的顶点 ,, 均在格点上.
(1)求 的面积.
(2)试判断 的形状,并说明理由.
如图,在四边形 中,,,,.分别以点 , 为圆心,大于 的长为半径作弧,两弧交于点 ,作射线 交 于点 ,交 于点 ,点 是 的中点.
(1)求证:;
(2)求 的长.
如图,要修建一个育苗棚,棚高 ,棚宽 ,棚的长为 ,现要在棚顶上覆盖塑料薄膜,试求需要多少平方米塑料薄膜?
如图,在 的正方形网格中,每个小格的顶点叫做格点,以格点为顶点分别按下列要求画三角形.
(1) 在图①中,画一个直角三角形,使它的三边长都是有理数;
(2) 在图②中,画一个直角三角形,使它的一边长是有理数,另外两边长是无理数;
(3) 在图③中,画一个直角三角形,使它的三边长都是无理数.
答案
1. C
2. A
3. A
4. C
5. C
6. D
7. C
8. B
9. D
10. C
11. B
12. B
13. A
14. B
15. B
16.
17. ①②③
18.
19. 直角
20. (1) 所以 的面积为 .
(2) 判断 是直角三角形.理由如下:因为 ,,,所以 .所以 是直角三角形.
21. (1) , , ,, , .
(2) 连接 ,易证 垂直平分 , ,由()知 , ,.在 中, , , , .
22. 平方米.
23. (1) 如答图①, 即为所求.(2) 如答图②, 即为所求.(答案不唯一)
(3) 如答图③, 即为所求.(答案不唯一)
