2021-2022学年华东师大版八年级数学上册12.2整式的乘法 期末综合复习训练(Word版含解析)
文档属性
| 名称 | 2021-2022学年华东师大版八年级数学上册12.2整式的乘法 期末综合复习训练(Word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 112.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-04 00:00:00 | ||
图片预览



文档简介
2021-2022学年华师大版八年级数学上册《整式的乘法》期末综合复习训练(附答案)
1.计算:﹣a2b (ab)﹣1=( )
A.a B.a3b2 C.﹣a D.﹣a3b2
2.计算:a2(a﹣2b)=( )
A.a3﹣a2b B.a3﹣2a2b C.a3﹣2ab2 D.a3﹣a2b2
3.计算2a3 5a3的结果是( )
A.10a6 B.10a9 C.7a3 D.7a6
4.如果(2x+m)与(x+3)的乘积中不含x的一次项,那么m的值为( )
A.﹣6 B.﹣3 C.0 D.1
5.今天数学课上,老师讲了单项式乘多项式,放学回到家,小明拿出课堂笔记复习,发现一道题:﹣7xy(2y﹣x﹣3)=﹣14xy2+7x2y□,□的地方被钢笔水弄污了,你认为□内应填写( )
A.+21xy B.﹣21xy C.﹣3 D.﹣10xy
6.已知m+n=3,mn=﹣1,则(1﹣m)(1﹣n)的值为( )
A.﹣3 B.﹣1 C.1 D.5
7.已知等式(x+p)(x+q)=x2+mx+36(p,q为正整数),则m的值不可能是( )
A.37 B.13 C.20 D.36
8.若(x+m)(x﹣5)=x2+nx﹣10,则mn﹣m+n的值是( )
A.﹣11 B.﹣7 C.﹣6 D.﹣5
9.若计算(x2+mx)(4x﹣8)所得的结果中不含x2项,则常数m的值为( )
A.1 B.﹣1 C.﹣2 D.2
10.已知﹣2xmy2与4x2yn﹣1的积与﹣x4y3是同类项,求mn( )
A.2 B.3 C.4 D.5
11.计算:(2a2)3﹣6a2 a4= .
12.计算:ab (a+1)= .
13.计算:(2x+1)(x﹣3)= .
14.(x2﹣mx+6)(4x﹣2)的积中不含x的二次项,则m的值是 .
15.已知M=(x﹣2)(x﹣6),N=(x﹣5)(x﹣3),则M与N的大小关系是 .
16.已知m﹣n=﹣1,mn=5,则(3﹣m)(3+n)的值为 .
17.计算(x+y)(x2﹣xy+y2)
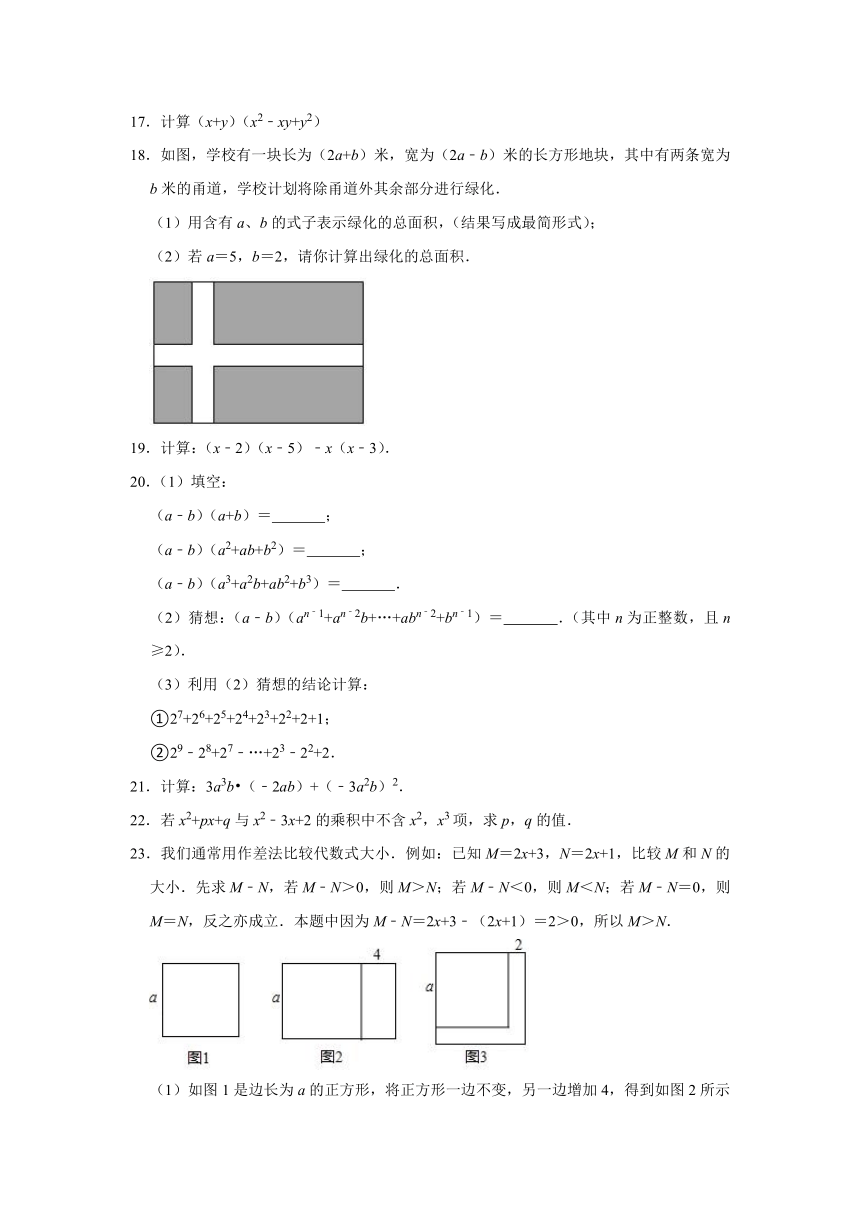
18.如图,学校有一块长为(2a+b)米,宽为(2a﹣b)米的长方形地块,其中有两条宽为b米的甬道,学校计划将除甬道外其余部分进行绿化.
(1)用含有a、b的式子表示绿化的总面积,(结果写成最简形式);
(2)若a=5,b=2,请你计算出绿化的总面积.
19.计算:(x﹣2)(x﹣5)﹣x(x﹣3).
20.(1)填空:
(a﹣b)(a+b)= ;
(a﹣b)(a2+ab+b2)= ;
(a﹣b)(a3+a2b+ab2+b3)= .
(2)猜想:(a﹣b)(an﹣1+an﹣2b+…+abn﹣2+bn﹣1)= .(其中n为正整数,且n≥2).
(3)利用(2)猜想的结论计算:
①27+26+25+24+23+22+2+1;
②29﹣28+27﹣…+23﹣22+2.
21.计算:3a3b (﹣2ab)+(﹣3a2b)2.
22.若x2+px+q与x2﹣3x+2的乘积中不含x2,x3项,求p,q的值.
23.我们通常用作差法比较代数式大小.例如:已知M=2x+3,N=2x+1,比较M和N的大小.先求M﹣N,若M﹣N>0,则M>N;若M﹣N<0,则M<N;若M﹣N=0,则M=N,反之亦成立.本题中因为M﹣N=2x+3﹣(2x+1)=2>0,所以M>N.
(1)如图1是边长为a的正方形,将正方形一边不变,另一边增加4,得到如图2所示的新长方形,此长方形的面积为S1;将图1中正方形边长增加2得到如图3所示的新正方形,此正方形的面积为S2.
①用含a的代数式分别表示S1和S2(结果需要化简);
②请用作差法比较S1与S2大小.
(2)若M=a2,N=4﹣(a+1)2,且M=N,求a(a+1)的值.
24.(1)如图是小颖家新房的户型图,小颖的爸爸打算把两个卧室以外的部分都铺上地砖,至少需要多少平方米的地砖?如果某种地砖的价格为每平方米a元,那么购买地砖至少需要多少元?
(2)如果房屋的高度是h米,现在需要在客厅和两个卧室四周的墙上贴墙纸,那么至少需要多少平方米的墙纸?如果某种墙纸的价格为每平方米b元,那么购买所需的墙纸至少要多少元?(计算时不扣除门、窗所占的面积,忽略墙的厚度)
25.已知(x﹣2)(x2﹣mx+n)的结果中不含x2项和x的项,求(m+n)(m2﹣mn+n2)的值.
参考答案
1.解:原式=﹣a2b a﹣1b﹣1
=﹣a2 a﹣1 b b﹣1
=﹣a2﹣1b1﹣1
=﹣a.
故选:C.
2.解:a2(a﹣2b)=a3﹣2a2b.
故选:B.
3.解:2a3 5a3=10a3+3=10a6,
故选:A.
4.解:(2x+m)(x+3)
=2x2+6x+mx+3m
=2x2+(6+m)x+3m,
∵(2x+m)与(x+3)的乘积中不含x的一次项,
∴6+m=0,
解得:m=﹣6,
故选:A.
5.解:﹣7xy(2y﹣x﹣3)=﹣14xy2+7x2y+21xy.
故选:A.
6.解:原式=1﹣n﹣m+mn
=1﹣(m+n)+mn,
∵m+n=3,mn=﹣1,
∴原式=1﹣3+(﹣1)=﹣3,
故选:A.
7.解:(x+p)(x+q)=x2+(p+q)x+pq,
∵(x+p)(x+q)=x2+mx+36,
∴p+q=m,pq=36,
∵36=4×9,则p+q=13,
36=1×36,则p+q=37,
36=2×18,则p+q=20,
36=3×12,则p+q=15,
36=6×6,则p+q=12,
∴p+q不可能为36,即m不可能为36.
故选:D.
8.解:(x+m)(x﹣5)
=x2﹣5x+mx﹣5m
=x2+(m﹣5)x﹣5m,
∵(x+m)(x﹣5)=x2+nx﹣10,
∴m﹣5=n,5m=10,
∴m=2,n=﹣3,
∴mn﹣m+n=2×(﹣3)﹣2+(﹣3)=﹣6﹣2﹣3=﹣11.
故选:A.
9.解:(x2+mx)(4x﹣8)
=4x3﹣8x2+4mx2﹣8mx
=4x3+(4m﹣8)x2﹣8mx,
∵不含x2项,
∴4m﹣8=0,
∴m=2.
故选:D.
10.解:(﹣2xmy2) (4x2yn﹣1)=﹣8xm+2yn+1,
∵﹣2xmy2与4x2yn﹣1的积与﹣x4y3是同类项,
∴m+2=4,n+1=3,
解得:m=2,n=2,
∴mn=4.
故选:C.
11.解:(2a2)3﹣6a2 a4
=8a6﹣6a6
=2a6,
故答案为:2a6.
12.解:原式=a2b+ab,
故答案为:a2b+ab.
13.解:原式=2x2﹣6x+x﹣3
=2x2﹣5x﹣3.
故答案是:2x2﹣5x﹣3.
14.解:原式=4x3﹣2x2﹣4mx2+2mx+24x﹣12
=4x3﹣(2+4m)x2+2mx+24x﹣12,
令2+4m=0,
∴m=﹣,
故答案为:.
15.解:∵M﹣N
=(x﹣2)(x﹣6)﹣(x﹣5)(x﹣3)
=x2﹣2x﹣6x+12﹣x2+3x+5x﹣15
=﹣3<0,
∴M<N,
故答案为:M<N.
16.解:(3﹣m)(3+n)
=9+3n﹣3m﹣mn
=9﹣3(m﹣n)﹣mn,
当m﹣n=﹣1,mn=5时,
原式=9﹣3×(﹣1)﹣5
=9﹣(﹣3)﹣5
=9+3﹣5
=7,
故答案为:7.
17.解:(x+y)(x2﹣xy+y2),
=x3﹣x2y+xy2+x2y﹣xy2+y3,
=x3+y3.
故答案为:x3+y3.
18.解:(1)绿化总面积=(2a+b﹣b)(2a﹣b﹣b)
=2a (2a﹣2b)
=4a2﹣4ab.
(2)当a=5,b=2时,
原式=4×52﹣4×5×2
=100﹣40
=60(米2).
19.解:原式=x2﹣5x﹣2x+10﹣x2+3x
=﹣4x+10,
故答案为:﹣4x+10.
20.解:(1)(a﹣b)(a+b)=a2﹣b2;
(a﹣b)(a2+ab+b2)=a3+a2b+ab2﹣a2b﹣ab2﹣b3=a3﹣b3;
(a﹣b)(a3+a2b+ab2+b3)=a4+a3b+a2b2+ab3﹣a3b﹣a2b2﹣ab3﹣b4=a4﹣b4;
故答案为:a2﹣b2;a3﹣b3;a4﹣b4.
(2)由(1)规律可得:原式=an﹣bn.
故答案为:an﹣bn.
(3)①27+26+25+24+23+22+2+1
=(2﹣1)(27+26+25+24+23+22+2+1)
=(2﹣1)(27+26×1+25×12+24×13+23×14+22×15+2×16+1)
=28﹣18
=255.
②∵[2﹣(﹣1)](29﹣28+27﹣…+23﹣22+2﹣1)=210﹣110,
∴.
∴29﹣28+27﹣…+23﹣22+2=341+1=342.
21.解:原式=﹣6a4b2+9a4b2
=3a4b2.
22.解:(x2+px+q)(x2﹣3x+2)
=x4﹣3x3+2x2+px3﹣3px2+2px+qx2﹣3qx+2q
=x4+(p﹣3)x3+(2﹣3p+q)x2+(2p﹣3q)x+2q
∵x2+px+q与x2﹣3x+2的乘积中不含x2,x3项,
∴p﹣3=0,2﹣3p+q=0.
∴p=3,q=7.
23.解:(1)①S1=a(a+4)=a2+4a,,
②∵,
∴S1<S2;
(2)由M=N,得到M﹣N=0,
∴a2﹣4+(a+1)2=0,
整理得:2a2+2a﹣3=0,
即2a2+2a=3,
则.
24.解:(1)由题意知,两个卧室以外的部分面积为:
3y y+2y (3x﹣x﹣y)
=3y2+4xy﹣2y2
=y2+4xy(平方米).
∴购买地砖所需的费用为:(y2+4xy)a=ay2+4axy(元).
(2)客厅贴墙纸的面积为:(2y+6y)h=8yh,
两个卧室贴墙纸的面积为:(4x+6y)h=4xh+6yh,
∴贴墙纸的总面积为:8yh+4xh+6yh=14yh+4xh(平方米),
∴购买墙纸所需的费用为:(14yh+4xh)b=14yhb+4xhb(元).
25.解:原式=x3﹣mx2+nx﹣2x2+2mx﹣2n=x3+(﹣m﹣2)x2+(n+2m)x﹣2n,
由结果不含x2项和x项,得到﹣m﹣2=0,n+2m=0,
解得:m=﹣2,n=4,
∴(m+n)(m2﹣mn+n2)=(﹣2+4)[(﹣2)2﹣(﹣2)×4+42]=2×28=56.
1.计算:﹣a2b (ab)﹣1=( )
A.a B.a3b2 C.﹣a D.﹣a3b2
2.计算:a2(a﹣2b)=( )
A.a3﹣a2b B.a3﹣2a2b C.a3﹣2ab2 D.a3﹣a2b2
3.计算2a3 5a3的结果是( )
A.10a6 B.10a9 C.7a3 D.7a6
4.如果(2x+m)与(x+3)的乘积中不含x的一次项,那么m的值为( )
A.﹣6 B.﹣3 C.0 D.1
5.今天数学课上,老师讲了单项式乘多项式,放学回到家,小明拿出课堂笔记复习,发现一道题:﹣7xy(2y﹣x﹣3)=﹣14xy2+7x2y□,□的地方被钢笔水弄污了,你认为□内应填写( )
A.+21xy B.﹣21xy C.﹣3 D.﹣10xy
6.已知m+n=3,mn=﹣1,则(1﹣m)(1﹣n)的值为( )
A.﹣3 B.﹣1 C.1 D.5
7.已知等式(x+p)(x+q)=x2+mx+36(p,q为正整数),则m的值不可能是( )
A.37 B.13 C.20 D.36
8.若(x+m)(x﹣5)=x2+nx﹣10,则mn﹣m+n的值是( )
A.﹣11 B.﹣7 C.﹣6 D.﹣5
9.若计算(x2+mx)(4x﹣8)所得的结果中不含x2项,则常数m的值为( )
A.1 B.﹣1 C.﹣2 D.2
10.已知﹣2xmy2与4x2yn﹣1的积与﹣x4y3是同类项,求mn( )
A.2 B.3 C.4 D.5
11.计算:(2a2)3﹣6a2 a4= .
12.计算:ab (a+1)= .
13.计算:(2x+1)(x﹣3)= .
14.(x2﹣mx+6)(4x﹣2)的积中不含x的二次项,则m的值是 .
15.已知M=(x﹣2)(x﹣6),N=(x﹣5)(x﹣3),则M与N的大小关系是 .
16.已知m﹣n=﹣1,mn=5,则(3﹣m)(3+n)的值为 .
17.计算(x+y)(x2﹣xy+y2)
18.如图,学校有一块长为(2a+b)米,宽为(2a﹣b)米的长方形地块,其中有两条宽为b米的甬道,学校计划将除甬道外其余部分进行绿化.
(1)用含有a、b的式子表示绿化的总面积,(结果写成最简形式);
(2)若a=5,b=2,请你计算出绿化的总面积.
19.计算:(x﹣2)(x﹣5)﹣x(x﹣3).
20.(1)填空:
(a﹣b)(a+b)= ;
(a﹣b)(a2+ab+b2)= ;
(a﹣b)(a3+a2b+ab2+b3)= .
(2)猜想:(a﹣b)(an﹣1+an﹣2b+…+abn﹣2+bn﹣1)= .(其中n为正整数,且n≥2).
(3)利用(2)猜想的结论计算:
①27+26+25+24+23+22+2+1;
②29﹣28+27﹣…+23﹣22+2.
21.计算:3a3b (﹣2ab)+(﹣3a2b)2.
22.若x2+px+q与x2﹣3x+2的乘积中不含x2,x3项,求p,q的值.
23.我们通常用作差法比较代数式大小.例如:已知M=2x+3,N=2x+1,比较M和N的大小.先求M﹣N,若M﹣N>0,则M>N;若M﹣N<0,则M<N;若M﹣N=0,则M=N,反之亦成立.本题中因为M﹣N=2x+3﹣(2x+1)=2>0,所以M>N.
(1)如图1是边长为a的正方形,将正方形一边不变,另一边增加4,得到如图2所示的新长方形,此长方形的面积为S1;将图1中正方形边长增加2得到如图3所示的新正方形,此正方形的面积为S2.
①用含a的代数式分别表示S1和S2(结果需要化简);
②请用作差法比较S1与S2大小.
(2)若M=a2,N=4﹣(a+1)2,且M=N,求a(a+1)的值.
24.(1)如图是小颖家新房的户型图,小颖的爸爸打算把两个卧室以外的部分都铺上地砖,至少需要多少平方米的地砖?如果某种地砖的价格为每平方米a元,那么购买地砖至少需要多少元?
(2)如果房屋的高度是h米,现在需要在客厅和两个卧室四周的墙上贴墙纸,那么至少需要多少平方米的墙纸?如果某种墙纸的价格为每平方米b元,那么购买所需的墙纸至少要多少元?(计算时不扣除门、窗所占的面积,忽略墙的厚度)
25.已知(x﹣2)(x2﹣mx+n)的结果中不含x2项和x的项,求(m+n)(m2﹣mn+n2)的值.
参考答案
1.解:原式=﹣a2b a﹣1b﹣1
=﹣a2 a﹣1 b b﹣1
=﹣a2﹣1b1﹣1
=﹣a.
故选:C.
2.解:a2(a﹣2b)=a3﹣2a2b.
故选:B.
3.解:2a3 5a3=10a3+3=10a6,
故选:A.
4.解:(2x+m)(x+3)
=2x2+6x+mx+3m
=2x2+(6+m)x+3m,
∵(2x+m)与(x+3)的乘积中不含x的一次项,
∴6+m=0,
解得:m=﹣6,
故选:A.
5.解:﹣7xy(2y﹣x﹣3)=﹣14xy2+7x2y+21xy.
故选:A.
6.解:原式=1﹣n﹣m+mn
=1﹣(m+n)+mn,
∵m+n=3,mn=﹣1,
∴原式=1﹣3+(﹣1)=﹣3,
故选:A.
7.解:(x+p)(x+q)=x2+(p+q)x+pq,
∵(x+p)(x+q)=x2+mx+36,
∴p+q=m,pq=36,
∵36=4×9,则p+q=13,
36=1×36,则p+q=37,
36=2×18,则p+q=20,
36=3×12,则p+q=15,
36=6×6,则p+q=12,
∴p+q不可能为36,即m不可能为36.
故选:D.
8.解:(x+m)(x﹣5)
=x2﹣5x+mx﹣5m
=x2+(m﹣5)x﹣5m,
∵(x+m)(x﹣5)=x2+nx﹣10,
∴m﹣5=n,5m=10,
∴m=2,n=﹣3,
∴mn﹣m+n=2×(﹣3)﹣2+(﹣3)=﹣6﹣2﹣3=﹣11.
故选:A.
9.解:(x2+mx)(4x﹣8)
=4x3﹣8x2+4mx2﹣8mx
=4x3+(4m﹣8)x2﹣8mx,
∵不含x2项,
∴4m﹣8=0,
∴m=2.
故选:D.
10.解:(﹣2xmy2) (4x2yn﹣1)=﹣8xm+2yn+1,
∵﹣2xmy2与4x2yn﹣1的积与﹣x4y3是同类项,
∴m+2=4,n+1=3,
解得:m=2,n=2,
∴mn=4.
故选:C.
11.解:(2a2)3﹣6a2 a4
=8a6﹣6a6
=2a6,
故答案为:2a6.
12.解:原式=a2b+ab,
故答案为:a2b+ab.
13.解:原式=2x2﹣6x+x﹣3
=2x2﹣5x﹣3.
故答案是:2x2﹣5x﹣3.
14.解:原式=4x3﹣2x2﹣4mx2+2mx+24x﹣12
=4x3﹣(2+4m)x2+2mx+24x﹣12,
令2+4m=0,
∴m=﹣,
故答案为:.
15.解:∵M﹣N
=(x﹣2)(x﹣6)﹣(x﹣5)(x﹣3)
=x2﹣2x﹣6x+12﹣x2+3x+5x﹣15
=﹣3<0,
∴M<N,
故答案为:M<N.
16.解:(3﹣m)(3+n)
=9+3n﹣3m﹣mn
=9﹣3(m﹣n)﹣mn,
当m﹣n=﹣1,mn=5时,
原式=9﹣3×(﹣1)﹣5
=9﹣(﹣3)﹣5
=9+3﹣5
=7,
故答案为:7.
17.解:(x+y)(x2﹣xy+y2),
=x3﹣x2y+xy2+x2y﹣xy2+y3,
=x3+y3.
故答案为:x3+y3.
18.解:(1)绿化总面积=(2a+b﹣b)(2a﹣b﹣b)
=2a (2a﹣2b)
=4a2﹣4ab.
(2)当a=5,b=2时,
原式=4×52﹣4×5×2
=100﹣40
=60(米2).
19.解:原式=x2﹣5x﹣2x+10﹣x2+3x
=﹣4x+10,
故答案为:﹣4x+10.
20.解:(1)(a﹣b)(a+b)=a2﹣b2;
(a﹣b)(a2+ab+b2)=a3+a2b+ab2﹣a2b﹣ab2﹣b3=a3﹣b3;
(a﹣b)(a3+a2b+ab2+b3)=a4+a3b+a2b2+ab3﹣a3b﹣a2b2﹣ab3﹣b4=a4﹣b4;
故答案为:a2﹣b2;a3﹣b3;a4﹣b4.
(2)由(1)规律可得:原式=an﹣bn.
故答案为:an﹣bn.
(3)①27+26+25+24+23+22+2+1
=(2﹣1)(27+26+25+24+23+22+2+1)
=(2﹣1)(27+26×1+25×12+24×13+23×14+22×15+2×16+1)
=28﹣18
=255.
②∵[2﹣(﹣1)](29﹣28+27﹣…+23﹣22+2﹣1)=210﹣110,
∴.
∴29﹣28+27﹣…+23﹣22+2=341+1=342.
21.解:原式=﹣6a4b2+9a4b2
=3a4b2.
22.解:(x2+px+q)(x2﹣3x+2)
=x4﹣3x3+2x2+px3﹣3px2+2px+qx2﹣3qx+2q
=x4+(p﹣3)x3+(2﹣3p+q)x2+(2p﹣3q)x+2q
∵x2+px+q与x2﹣3x+2的乘积中不含x2,x3项,
∴p﹣3=0,2﹣3p+q=0.
∴p=3,q=7.
23.解:(1)①S1=a(a+4)=a2+4a,,
②∵,
∴S1<S2;
(2)由M=N,得到M﹣N=0,
∴a2﹣4+(a+1)2=0,
整理得:2a2+2a﹣3=0,
即2a2+2a=3,
则.
24.解:(1)由题意知,两个卧室以外的部分面积为:
3y y+2y (3x﹣x﹣y)
=3y2+4xy﹣2y2
=y2+4xy(平方米).
∴购买地砖所需的费用为:(y2+4xy)a=ay2+4axy(元).
(2)客厅贴墙纸的面积为:(2y+6y)h=8yh,
两个卧室贴墙纸的面积为:(4x+6y)h=4xh+6yh,
∴贴墙纸的总面积为:8yh+4xh+6yh=14yh+4xh(平方米),
∴购买墙纸所需的费用为:(14yh+4xh)b=14yhb+4xhb(元).
25.解:原式=x3﹣mx2+nx﹣2x2+2mx﹣2n=x3+(﹣m﹣2)x2+(n+2m)x﹣2n,
由结果不含x2项和x项,得到﹣m﹣2=0,n+2m=0,
解得:m=﹣2,n=4,
∴(m+n)(m2﹣mn+n2)=(﹣2+4)[(﹣2)2﹣(﹣2)×4+42]=2×28=56.
