2021-2022学年华东师大版九年级数学上册第二十四章解直角三角形 期末综合复习训练(Word版含解析)
文档属性
| 名称 | 2021-2022学年华东师大版九年级数学上册第二十四章解直角三角形 期末综合复习训练(Word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 524.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2022-01-04 23:29:52 | ||
图片预览




文档简介
2021-2022学年华师大版九年级数学上册《解直角三角形》期末综合复习训练(附答案)
1.如图,点A,B,C在正方形网格的格点上,则sin∠BAC等于( )
A. B. C. D.
2.如图,在C处测得旗杆AB的顶端A的仰角为30°,向旗杆前进10米到达D处,在D处测得A的仰角为60°,则旗杆的高为( )米.
A.5+3 B.10 C.5 D.5+5
3.如图,垂直于地面的通信基地AB建在陡峭的山坡BC上,该山坡的坡度i=1:2.4.小明为了测得通信基地AB的高度,他首先在C处测得山脚与通信基地AB的水平距离CD=156米,然后沿着斜坡走了52米到达E处,他在E处测得通信基地顶端A的仰角为60°,则通信基地AB的高度约为( )(参考数据:≈1.414,≈1.732)
A.136米 B.142米 C.148米 D.87米
4.如图,△ABC的顶点在正方形网格的格点上,则cos∠ACB的值为( )
A. B. C. D.
5.如图1,是我们经常看到的一种折叠桌子,它是由下面的支架AD、BC与桌面构成,如图2,已知OA=OB=OC=OD=20cm,∠COD=60°,则点A到地面(CD所在的平面)的距离是( )
A.30cm B.60cm C.40cm D.60cm
6.如图,一个长方体木箱沿斜面滑至如图位置时,AB=2m,木箱高BE=1m,斜面坡角为α,则木箱端点E距地面AC的高度表示为( )m.
A.+2sinα B.2cosα+sinα
C.cosα+2sinα D.tanα+2sinα
7.在如图所示的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,连接AB、AC,则sin∠BAC的值为( )
A. B. C. D.
8.如图,在四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=,则CD的值为( )
A.2 B. C. D.
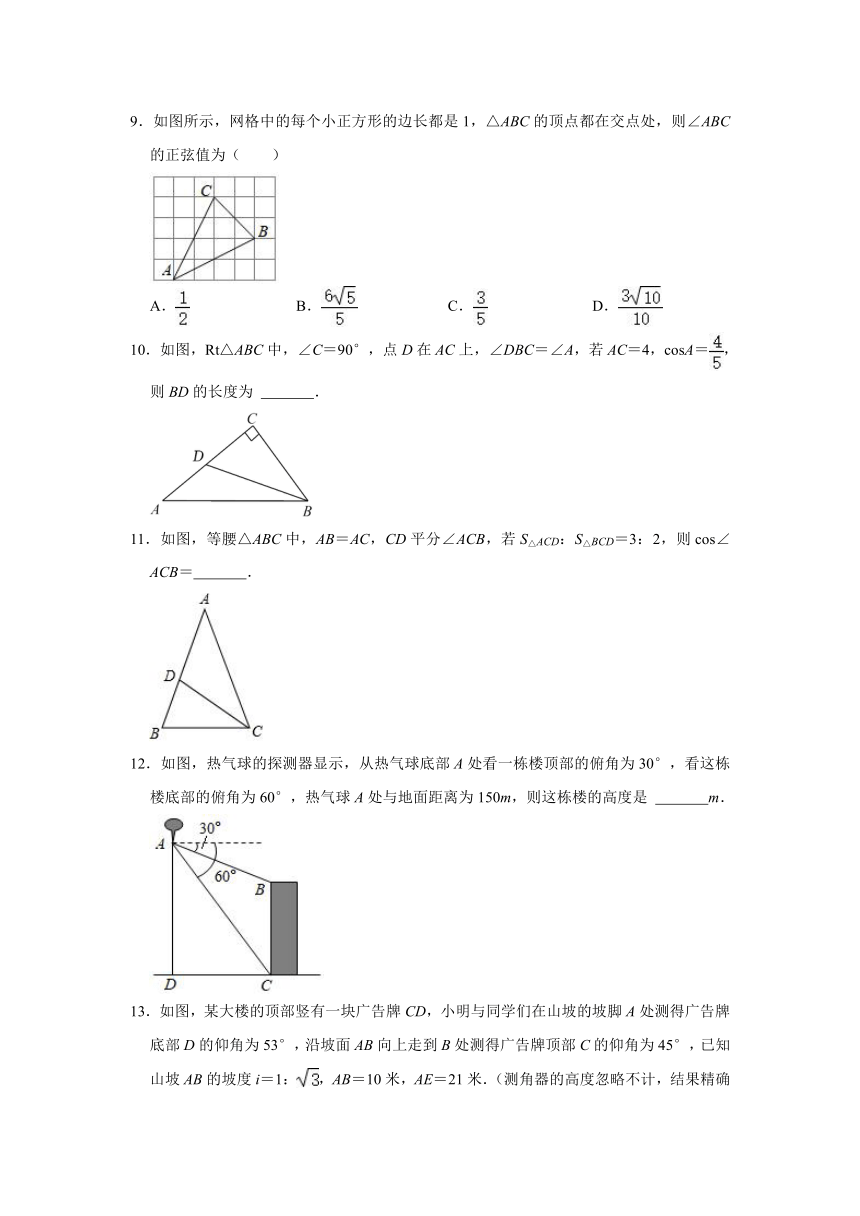
9.如图所示,网格中的每个小正方形的边长都是1,△ABC的顶点都在交点处,则∠ABC的正弦值为( )
A. B. C. D.
10.如图,Rt△ABC中,∠C=90°,点D在AC上,∠DBC=∠A,若AC=4,cosA=,则BD的长度为 .
11.如图,等腰△ABC中,AB=AC,CD平分∠ACB,若S△ACD:S△BCD=3:2,则cos∠ACB= .
12.如图,热气球的探测器显示,从热气球底部A处看一栋楼顶部的俯角为30°,看这栋楼底部的俯角为60°,热气球A处与地面距离为150m,则这栋楼的高度是 m.
13.如图,某大楼的顶部竖有一块广告牌CD,小明与同学们在山坡的坡脚A处测得广告牌底部D的仰角为53°,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:,AB=10米,AE=21米.(测角器的高度忽略不计,结果精确到0.1米,参考数据:≈1.41,≈1.73,sin53°≈,cos53°≈,tan53°≈)
(1)求点B距水平地面AE的高度;
(2)求广告牌CD的高度.(结果精确到0.1米)
14.测量计算是日常生活中常见的问题,如图,建筑物BC的屋顶有一根旗杆AB,从地面上D点处观测旗杆顶点A的仰角为50°,观测旗杆底部B点的仰角为45°.若已知旗杆的高度AB=5米,求建筑物BC的高度.(参考数据:sin50°≈0.8,tan50°≈1.2)
15.如图某船由西向东航行,在点A处测得小岛O在北偏东60°方向,船航行了10海里后到达点B.这时测得小岛O在北偏东45°方向,船继续航行到点C时,测得小岛O恰好在船的正北方,求此时船到小岛的距离.(结果保留根号)
16.如图,为了测量旗杆AB的高,一位学生在教学楼距地面6m高的窗口C处,测得正前方旗杆顶部A点的仰角为59°,旗杆底部B点的俯角为45°.求旗杆AB的高.(结果
精确到个位)[参考数据:sin59°=0.86,cos59°=0.52,tan59°=1.67]
17.如图,楼顶上有一个广告牌AB,从与楼BC相距12米的D处测得广告牌顶部A的仰角为37°,测得广告牌底部B的仰角为30°,求广告牌AB的高度.(结果保留根号,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
18.如图,从热气球C上测得两建筑物A、B底部的俯角分别为29.5°和45°,如果这时气球的高度CD为80米,且点A、D、B在同一直线上,求建筑物A、B之间的距离(结果精确到1米).
[参考数据:sin29.5°≈0.49,cos29.5°≈0.87,tan29.5°≈0.57]
19.2021年9月16号,泸县发生地震,救援队及时达到现场参与救援,在救援中用热气球进行探测.如图,探测器显示,从热气球看一栋高楼的顶部B的仰角(∠BAD)为45°,看这栋高楼底部C的俯角(∠CAD)为60°,热气球与高楼的水平距离AD为50m,求这栋高楼的高度(结果保留根号).
20.如图,平地上两栋建筑物AB和CD相距30m,在建筑物AB的顶部测得建筑物CD底部的俯角为26.6°,测得建筑物CD顶部的仰角为45°.求建筑物CD的高度.(参考数据:sin26.6°≈0.45,cos26.6°≈0.89,tan26.6°≈0.50)
21.大汉雄风坐落于河南省永城市芒砀山主峰,是为纪念刘邦在芒砀山斩蛇起义创建四百年大汉王朝而建,某数学兴趣小组想测量底座之上部分雕像AB的高度,如图在和雕塑底座上端水平的山坡C处测得雕塑顶端B的仰角为58.5°,沿山坡上行10米到达点D,测得雕塑顶端B的仰角为45°,已知山坡的坡度i=1:3,且A,C在同一水平地面上,求塑像AB的高度.(测倾器高度忽略不计,结果精确到0.1米,参考数据:sin58.5°≈0.85,cos58.5°≈0.52,tan58.5°≈1.63,≈1.4,≈1.7,≈3.2.)
22.如图,大楼AB高10米,远处有一雕像(含底座).某人在楼顶A测得雕像顶C点的仰角为30°,此人从楼底B向雕像水平方向前进2米到达点E,在E处测得C点的仰角为53°.已知雕像底座DF的高是8米,求雕像CF的高.(参考数据:sin53°=,cos53°=,tan53°=,≈1.7,计算结果精确到1m.)
23.如图,小明家在A处,门前有一口池塘,隔着池塘有一条公路l,AB是A到l的小路.现新修一条路AC到公路l,小明测量出∠ACD=31°,∠ABD=45°,BC=60m.请你帮小明计算他家到公路l的距离AD的长度?(精确到0.1m;参考数据tan31°≈0.60,sin31°≈0.51,cos31°≈0.86).
24.为了丰富学生的文化生活,学校利用假期组织学生到红色文化基地A和人工智能科技馆C参观学习.如图,学校在点B处,A位于学校的东北方向,C位于学校南偏东30°方向,C在A的南偏西15°方向(30+30)km处.学生分成两组,第一组前往A地,第二组前往C地,两组同学同时从学校出发,第一组乘客车,速度是40km/h,第二组乘公交车,速度是35km/h.
(1)求学校到红色文化基地A的距离?
(2)哪组同学先到达目的地?请说明理由(结果保留根号).
25.如图,在△ABC中,∠C=90°,点D,E分别在AC,AB上,BD平分∠ABC,DE⊥AB于点E,AE=6,cosA=.
(1)求CD的长;
(2)求tan∠DBC的值.
26.如图,一艘渔船位于小岛B的北偏东30°方向,距离小岛80nmile的点A处,它沿着点A的南偏东15°方向航行.
(1)渔船航行多远与小岛B的距离最近?(结果保留根号)
(2)渔船到达距离小岛B最近点后,按原航向继续航行40nmile到点C处时突然发生事故,渔船马上向小岛B上的救援队求救,问:救援队从B处出发沿着哪个方向航行到达事故地点航程最短,最短航程是多少?(结果保留根号)
参考答案
1.解:连接CD,点D在格点上,如右图所示:
设每个小正方形的边长为a,
则CD==a,
AC==a,
AD==2a,
∴CD2+AD2=(a)2+(2a)2=(a)2=AC2,
∴△ACD是直角三角形,
∴sin∠BAC=sin∠CAD===,
故选:D.
2.解:由题意得:∠C=30°,∠ADB=60°,
∴∠DAC=∠ADB﹣∠C=30°,
∴∠DAC=∠C,
∴AD=DC=10米,
在Rt△ADB中,sin∠ADB=,
则AB=AD sin∠ADB=10×=5(米),
故选:C.
3.解:如图作EH⊥CD于H,EF⊥AD于F.
在Rt△ECH中,∵EH:CH=1:2.4,EC=52m,
∴EH=DF=20m,CH=48m,
∴EF=DH=CD﹣CH=156﹣48=108m,
在Rt△AEF中,∵∠AEF=60°,
∴AF=EF tan60°=108,
∴AD=AF+DF=108+20≈207m,
在Rt△BCD中,∵BD:CD=1:2.4,
∴BD=65m,
∴AB=AD﹣BD=207﹣65=142m,
故选:B.
4.解:过A作AD⊥BC于D,
∴DC=1,AD=3,
∴AC=,
∴cos∠ACB=,
故选:D.
5.解:如图,连接CD,过O作OF⊥CD于点F,延长FO,交AB于点E,
∵OA=OB=OC=OD=20cm,∠COD=60°,
∴∠COF=30°,
∴OF=OC cos∠COF==30(cm),
∴EF=2OF=60(cm),
即点A到地面(CD所在的平面)的距离是60cm.
故选:D.
6.解:过E作EN⊥AC于N,交AB于M,过B作BG⊥AC于G,BH⊥EN于H,如图所示:
则四边形BHNG是矩形,
∴HN=BG,
在Rt△ABG中,∠BAG=α,sin∠BAG=,
∴BG=AB sin∠BAG=2sinα(m),
∴HN=2sinα(m),
∵∠EBM=∠ANM=90°,∠BME=∠AMN,
∴∠BEM=∠MAN=α,
在Rt△EHB中,∠BEM=α,BE=1m,
∵oos∠BEM=,
∴EH=BE cos∠BEM=1×cosα=cosα(m),
∴EN=EH+HN=(cosα+2sinα)m,
即木箱端点E距地面AC的高度为(cosα+2sinα)m,
故选:C.
7.解:连接BC,
∵AC2=42+22=20,
AB2=32+42=25,
BC2=12+22=5,
∴AC2+BC2=AB2.
∴∠ACB=90°.
∴sin∠BAC==.
故选:B.
8.解:延长AD、BC,两线交于O,
在Rt△ABO中,∠B=90°,tanA==,AB=3,
∴OB=4,
∵BC=2,
∴OC=OB﹣BC=4﹣2=2,
在Rt△ABO中,∠B=90°,AB=3,OB=4,
由勾股定理得:AO=5,
∵∠ADC=90°,
∴∠ODC=90°=∠B,
∵∠O=∠O,
∴△ODC∽△OBA,
∴=,
∴=,
解得:DC=,
故选:D.
9.解:如图,取BC的中点D,连接AD,
由网格可得,AC=AB==2,
∴AD⊥BC,
Rt△ABD中,
∵AD==3,
∴sin∠ABC===.
故选:D.
10.解:∵∠C=90°,AC=4,cosA=,
∴AB=5,
∴BC===3,
∵∠DBC=∠A.
∴cos∠DBC=cos∠A==,
∴BD=3×=,
故答案为:.
11.解:如图,过点A作AE⊥BC于点E,DN⊥AC于N,DM⊥BC于M.
∵CD平分∠ACB,DM⊥BC于M,DN⊥AC于点N,
∴DM=DN.
∵,,
∴S△ACD:S△BCD=AC:BC=3:2.
∵AB=AC,AE⊥BC,
∴BE=CE=.
∴CE:AC=1:3.
∴cos∠ACB=.
故答案为:.
12.解:如图,过A作AH⊥BC,交CB的延长线于点H,
在Rt△ACD中,
∵∠CAD=30°,AD=150m,
∴CD=AD tan30°=150×=50(m),
∴AH=CD=50m.
在Rt△ABH中,
∵∠BAH=30°,AH=50m,
∴BH=AH tan30°=50×=50(m),
∴BC=AD﹣BH=150﹣50=100(m),
答:这栋楼的高度为100m.
故答案为:100.
13.解:(1)如图,过点B作BM⊥AE,BN⊥CE,垂足分别为M、N,
由题意可知,∠CBN=45°,∠DAE=53°,i=1:,AB=10米,AE=21米.
∵i=1:==tan∠BAM,
∴∠BAM=30°,
∴BM=AB=5(米),
即点B距水平地面AE的高度为5米;
(2)在Rt△ABM中,∠BAM=30°,
∴BM=AB=5(米)=NE,AM=AB=5(米),
∴ME=AM+AE=(5+21)米=BN,
∵∠CBN=45°,
∴CN=BN=ME=(5+21)米,
∴CE=CN+NE=(5+26)米,
在Rt△ADE中,∠DAE=53°,AE=21米,
∴DE=AE tan53°≈21×=28(米),
∴CD=CE﹣DE=5+26﹣28=5﹣2≈6.7(米),
即广告牌CD的高度约为6.7米.
14.解:设BC=x米,则AC=(x+5)米,
在Rt△BDC中,∠BDC=45°,
∴DC=BC=x米,
在Rt△ADC中,tan∠ADC=,即=1.2,
解得:x=25,
答:建筑物BC的高度为25米.
15.解:设OC=x海里,
依题意得∠OAB=30°,∠OBC=∠BOC=45°,作OC⊥AB,
∴BC=OC=x海里,AC=x海里,
∵AC﹣BC=10,
∴(﹣1)x=10,
解得x==5(+1),
答:船与小岛的距离是5(+1)海里.
16.解:过C作CD⊥AB于D,
则∠ACD=59°,∠DCB=45°,BD=6m,
在Rt△BCD中,∵∠BDC=90°,∠BCD=45°,
∴△BCD是等腰直角三角形,
∴BD=CD=6(m),
在Rt△ADC中,∠ADC=90°,∠ACD=59°,
∴tan59°=,
∴AD=CD tan59°≈6×1.67≈10(m),
∴AB=AD+BD=10+6=16(m),
答:旗杆AB的高约为16m.
17.解:在Rt△BCD中,BC=DC tan30°=12×=4(m),
在Rt△ACD中,AC=DC tan37°≈12×0.75=9(m),
∴AB=AC﹣BC=(9﹣4)(m).
答:广告牌AB的高度约为(9﹣4)m.
18.解:由已知得:∠ECA=29.5°,∠FCB=45°,CD=80米,EF∥AB,CD⊥AB,
∴∠A=∠ECA=29.5°,∠B=∠FCB=45°,
∴△BCD是等腰直角三角形,
∴BD=CD=80米,
在Rt△ACD中,∠CDA=90°,tanA=,
∴AD==≈140.4(米),
∴AB=AD+BD≈140.4+80≈220(米),
即建筑物A、B之间的距离约为220米.
19.解:在Rt△ABD中,tan∠BAD=,
∴BD=ADtan45°=50×1=50(m),
在Rt△ADC中,tan∠CAD=,
∴CD=ADtan60°=50×=50(m),
∴BC=BD+CD=(50+50)m,
答:这栋高楼的高度为(50+50)m.
20.解:过A点作AE⊥CD于E点,
由题意得,四边形ABDE为矩形,
∵∠DAE=26.6°,BD=30m,
∴AE=BD=30m,tan26.6°=,
∴DE=tan26.6° AE=0.50×30=15m,
∵∠CAE=45°,
∴∠ACE=45°,
∴AE=EC,
∴CE=30m,
∴CD=CE+ED=30+15=45(m),
∴建筑物CD的高度是45m.
21.解:过点 D作 DE⊥AC 交 AC于点 E,DF⊥AB交 AB于点 F,
∵i=1:3,CD=10,
设 DE=xm,则 CE=3xm,
在 Rt△CED 中,x2+(3x)2=102,
解得:x=或x=﹣(舍),
∴DE=m,则CE=3m,
∵∠BDF=∠DBF=45°,
∴BF=DF,
设 BF=DF=m 米,则 AB=(m+)米,AC=(m﹣3)米,
在 Rt△CAB 中,,
解得:m≈29.9,
∴AB=29.9+≈33.1(米),
答:塑像的高度约为 33.1米.
22.解:如图,过点A作AG⊥CD于G,设CD=x,
∴四边形ABDG是矩形,
∴AG=BD,GD=AB,
∵∠CED=53°,
∴DE=,
∴AG=BD=+2,
∵∠CAG=30°,
∴CG=AG tan30°,即CD﹣GD=AG tan30°,
∴,
解得:x≈20,
∴CF=CD﹣DF=20﹣8=12(米),
答:雕像CF的高为12米.
23.解:设AD=xm,
∵∠ABD=45°,
∴BD=AD=xm,
∵∠ACD=31°,BC=60m,
∴tan31°==≈0.60,
解得x=90.0,
∴他家到公路l的距离AD的长度约90.0m.
24.解:(1)作BD⊥AC于D.
依题意得,
∠BAE=45°,∠ABC=105°,∠CAE=15°,
∴∠BAC=30°,
∴∠ACB=45°.
在Rt△BCD中,∠BDC=90°,∠ACB=45°,
∴∠CBD=45°,
∴∠CBD=∠DCB,
∴BD=CD,
设BD=xkm,则CD=xkm,
在Rt△ABD中,∠BAC=30°,
∴AB=2BD=2xkm,tan30°=,
∴=,
∴AD=x,
在Rt△BDC中,∠BDC=90°,∠DCB=45°,
∴sin∠DCB==,
∴BC=x,
∵CD+AD=30+30,
∴x+x=30+30,
∴x=30,
∴AB=2x=60(km);
(2)第二组先到达目的地,
理由:∵BD=30km,
∴BC=x=30km,
第一组用时:60÷40=1.5(h);第二组用时:30÷35=(h),
∵<1.5,
∴第二组先到达目的地,
答:第二组先到达目的地.
25.解:(1)在Rt△ADE中,∠AED=90°,AE=6,cosA=,
∴AD==10,
∴==8.
∵BD平分∠ABC,DE⊥AB,DC⊥BC,
∴CD=DE=8;
(2)由(1)AD=10,DC=8,
∴AC=AD+DC=18,
在△ADE与△ABC中,
∵∠A=∠A,∠AED=∠ACB,
∴△ADE∽△ABC,
∴,即=,
∴BC=24,
∴.
26.解:(1)过点B作BM⊥AC于点M,如图所示:
由题意,知∠BAM=45°,则∠ABM=45°.
在Rt△ABM中,∠BAM=45°,AB=80nmile,
∴△ABM是等腰直角三角形,
∴BM=AM=AB=40(nmile)
答:渔船航行40nmile与小岛B的距离最近.
(2)∵BM=40nmile,MC=40nmile,
∴,
∴∠MBC=60°,
∴∠CBG=180°﹣60°﹣45°﹣30°=45°,
在Rt△BCM中,∠MBC=60°,
∴∠BCM=30°,
∴BC=2BM=80(nmile),
答:救援队从B处出发沿着点B的南偏东45°方向航行到达事故地点航程最短,最短航程是80nmile.
1.如图,点A,B,C在正方形网格的格点上,则sin∠BAC等于( )
A. B. C. D.
2.如图,在C处测得旗杆AB的顶端A的仰角为30°,向旗杆前进10米到达D处,在D处测得A的仰角为60°,则旗杆的高为( )米.
A.5+3 B.10 C.5 D.5+5
3.如图,垂直于地面的通信基地AB建在陡峭的山坡BC上,该山坡的坡度i=1:2.4.小明为了测得通信基地AB的高度,他首先在C处测得山脚与通信基地AB的水平距离CD=156米,然后沿着斜坡走了52米到达E处,他在E处测得通信基地顶端A的仰角为60°,则通信基地AB的高度约为( )(参考数据:≈1.414,≈1.732)
A.136米 B.142米 C.148米 D.87米
4.如图,△ABC的顶点在正方形网格的格点上,则cos∠ACB的值为( )
A. B. C. D.
5.如图1,是我们经常看到的一种折叠桌子,它是由下面的支架AD、BC与桌面构成,如图2,已知OA=OB=OC=OD=20cm,∠COD=60°,则点A到地面(CD所在的平面)的距离是( )
A.30cm B.60cm C.40cm D.60cm
6.如图,一个长方体木箱沿斜面滑至如图位置时,AB=2m,木箱高BE=1m,斜面坡角为α,则木箱端点E距地面AC的高度表示为( )m.
A.+2sinα B.2cosα+sinα
C.cosα+2sinα D.tanα+2sinα
7.在如图所示的网格中,每个小正方形的边长均为1,点A,B,C都在格点上,连接AB、AC,则sin∠BAC的值为( )
A. B. C. D.
8.如图,在四边形ABCD中,∠B=∠D=90°,AB=3,BC=2,tanA=,则CD的值为( )
A.2 B. C. D.
9.如图所示,网格中的每个小正方形的边长都是1,△ABC的顶点都在交点处,则∠ABC的正弦值为( )
A. B. C. D.
10.如图,Rt△ABC中,∠C=90°,点D在AC上,∠DBC=∠A,若AC=4,cosA=,则BD的长度为 .
11.如图,等腰△ABC中,AB=AC,CD平分∠ACB,若S△ACD:S△BCD=3:2,则cos∠ACB= .
12.如图,热气球的探测器显示,从热气球底部A处看一栋楼顶部的俯角为30°,看这栋楼底部的俯角为60°,热气球A处与地面距离为150m,则这栋楼的高度是 m.
13.如图,某大楼的顶部竖有一块广告牌CD,小明与同学们在山坡的坡脚A处测得广告牌底部D的仰角为53°,沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:,AB=10米,AE=21米.(测角器的高度忽略不计,结果精确到0.1米,参考数据:≈1.41,≈1.73,sin53°≈,cos53°≈,tan53°≈)
(1)求点B距水平地面AE的高度;
(2)求广告牌CD的高度.(结果精确到0.1米)
14.测量计算是日常生活中常见的问题,如图,建筑物BC的屋顶有一根旗杆AB,从地面上D点处观测旗杆顶点A的仰角为50°,观测旗杆底部B点的仰角为45°.若已知旗杆的高度AB=5米,求建筑物BC的高度.(参考数据:sin50°≈0.8,tan50°≈1.2)
15.如图某船由西向东航行,在点A处测得小岛O在北偏东60°方向,船航行了10海里后到达点B.这时测得小岛O在北偏东45°方向,船继续航行到点C时,测得小岛O恰好在船的正北方,求此时船到小岛的距离.(结果保留根号)
16.如图,为了测量旗杆AB的高,一位学生在教学楼距地面6m高的窗口C处,测得正前方旗杆顶部A点的仰角为59°,旗杆底部B点的俯角为45°.求旗杆AB的高.(结果
精确到个位)[参考数据:sin59°=0.86,cos59°=0.52,tan59°=1.67]
17.如图,楼顶上有一个广告牌AB,从与楼BC相距12米的D处测得广告牌顶部A的仰角为37°,测得广告牌底部B的仰角为30°,求广告牌AB的高度.(结果保留根号,参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
18.如图,从热气球C上测得两建筑物A、B底部的俯角分别为29.5°和45°,如果这时气球的高度CD为80米,且点A、D、B在同一直线上,求建筑物A、B之间的距离(结果精确到1米).
[参考数据:sin29.5°≈0.49,cos29.5°≈0.87,tan29.5°≈0.57]
19.2021年9月16号,泸县发生地震,救援队及时达到现场参与救援,在救援中用热气球进行探测.如图,探测器显示,从热气球看一栋高楼的顶部B的仰角(∠BAD)为45°,看这栋高楼底部C的俯角(∠CAD)为60°,热气球与高楼的水平距离AD为50m,求这栋高楼的高度(结果保留根号).
20.如图,平地上两栋建筑物AB和CD相距30m,在建筑物AB的顶部测得建筑物CD底部的俯角为26.6°,测得建筑物CD顶部的仰角为45°.求建筑物CD的高度.(参考数据:sin26.6°≈0.45,cos26.6°≈0.89,tan26.6°≈0.50)
21.大汉雄风坐落于河南省永城市芒砀山主峰,是为纪念刘邦在芒砀山斩蛇起义创建四百年大汉王朝而建,某数学兴趣小组想测量底座之上部分雕像AB的高度,如图在和雕塑底座上端水平的山坡C处测得雕塑顶端B的仰角为58.5°,沿山坡上行10米到达点D,测得雕塑顶端B的仰角为45°,已知山坡的坡度i=1:3,且A,C在同一水平地面上,求塑像AB的高度.(测倾器高度忽略不计,结果精确到0.1米,参考数据:sin58.5°≈0.85,cos58.5°≈0.52,tan58.5°≈1.63,≈1.4,≈1.7,≈3.2.)
22.如图,大楼AB高10米,远处有一雕像(含底座).某人在楼顶A测得雕像顶C点的仰角为30°,此人从楼底B向雕像水平方向前进2米到达点E,在E处测得C点的仰角为53°.已知雕像底座DF的高是8米,求雕像CF的高.(参考数据:sin53°=,cos53°=,tan53°=,≈1.7,计算结果精确到1m.)
23.如图,小明家在A处,门前有一口池塘,隔着池塘有一条公路l,AB是A到l的小路.现新修一条路AC到公路l,小明测量出∠ACD=31°,∠ABD=45°,BC=60m.请你帮小明计算他家到公路l的距离AD的长度?(精确到0.1m;参考数据tan31°≈0.60,sin31°≈0.51,cos31°≈0.86).
24.为了丰富学生的文化生活,学校利用假期组织学生到红色文化基地A和人工智能科技馆C参观学习.如图,学校在点B处,A位于学校的东北方向,C位于学校南偏东30°方向,C在A的南偏西15°方向(30+30)km处.学生分成两组,第一组前往A地,第二组前往C地,两组同学同时从学校出发,第一组乘客车,速度是40km/h,第二组乘公交车,速度是35km/h.
(1)求学校到红色文化基地A的距离?
(2)哪组同学先到达目的地?请说明理由(结果保留根号).
25.如图,在△ABC中,∠C=90°,点D,E分别在AC,AB上,BD平分∠ABC,DE⊥AB于点E,AE=6,cosA=.
(1)求CD的长;
(2)求tan∠DBC的值.
26.如图,一艘渔船位于小岛B的北偏东30°方向,距离小岛80nmile的点A处,它沿着点A的南偏东15°方向航行.
(1)渔船航行多远与小岛B的距离最近?(结果保留根号)
(2)渔船到达距离小岛B最近点后,按原航向继续航行40nmile到点C处时突然发生事故,渔船马上向小岛B上的救援队求救,问:救援队从B处出发沿着哪个方向航行到达事故地点航程最短,最短航程是多少?(结果保留根号)
参考答案
1.解:连接CD,点D在格点上,如右图所示:
设每个小正方形的边长为a,
则CD==a,
AC==a,
AD==2a,
∴CD2+AD2=(a)2+(2a)2=(a)2=AC2,
∴△ACD是直角三角形,
∴sin∠BAC=sin∠CAD===,
故选:D.
2.解:由题意得:∠C=30°,∠ADB=60°,
∴∠DAC=∠ADB﹣∠C=30°,
∴∠DAC=∠C,
∴AD=DC=10米,
在Rt△ADB中,sin∠ADB=,
则AB=AD sin∠ADB=10×=5(米),
故选:C.
3.解:如图作EH⊥CD于H,EF⊥AD于F.
在Rt△ECH中,∵EH:CH=1:2.4,EC=52m,
∴EH=DF=20m,CH=48m,
∴EF=DH=CD﹣CH=156﹣48=108m,
在Rt△AEF中,∵∠AEF=60°,
∴AF=EF tan60°=108,
∴AD=AF+DF=108+20≈207m,
在Rt△BCD中,∵BD:CD=1:2.4,
∴BD=65m,
∴AB=AD﹣BD=207﹣65=142m,
故选:B.
4.解:过A作AD⊥BC于D,
∴DC=1,AD=3,
∴AC=,
∴cos∠ACB=,
故选:D.
5.解:如图,连接CD,过O作OF⊥CD于点F,延长FO,交AB于点E,
∵OA=OB=OC=OD=20cm,∠COD=60°,
∴∠COF=30°,
∴OF=OC cos∠COF==30(cm),
∴EF=2OF=60(cm),
即点A到地面(CD所在的平面)的距离是60cm.
故选:D.
6.解:过E作EN⊥AC于N,交AB于M,过B作BG⊥AC于G,BH⊥EN于H,如图所示:
则四边形BHNG是矩形,
∴HN=BG,
在Rt△ABG中,∠BAG=α,sin∠BAG=,
∴BG=AB sin∠BAG=2sinα(m),
∴HN=2sinα(m),
∵∠EBM=∠ANM=90°,∠BME=∠AMN,
∴∠BEM=∠MAN=α,
在Rt△EHB中,∠BEM=α,BE=1m,
∵oos∠BEM=,
∴EH=BE cos∠BEM=1×cosα=cosα(m),
∴EN=EH+HN=(cosα+2sinα)m,
即木箱端点E距地面AC的高度为(cosα+2sinα)m,
故选:C.
7.解:连接BC,
∵AC2=42+22=20,
AB2=32+42=25,
BC2=12+22=5,
∴AC2+BC2=AB2.
∴∠ACB=90°.
∴sin∠BAC==.
故选:B.
8.解:延长AD、BC,两线交于O,
在Rt△ABO中,∠B=90°,tanA==,AB=3,
∴OB=4,
∵BC=2,
∴OC=OB﹣BC=4﹣2=2,
在Rt△ABO中,∠B=90°,AB=3,OB=4,
由勾股定理得:AO=5,
∵∠ADC=90°,
∴∠ODC=90°=∠B,
∵∠O=∠O,
∴△ODC∽△OBA,
∴=,
∴=,
解得:DC=,
故选:D.
9.解:如图,取BC的中点D,连接AD,
由网格可得,AC=AB==2,
∴AD⊥BC,
Rt△ABD中,
∵AD==3,
∴sin∠ABC===.
故选:D.
10.解:∵∠C=90°,AC=4,cosA=,
∴AB=5,
∴BC===3,
∵∠DBC=∠A.
∴cos∠DBC=cos∠A==,
∴BD=3×=,
故答案为:.
11.解:如图,过点A作AE⊥BC于点E,DN⊥AC于N,DM⊥BC于M.
∵CD平分∠ACB,DM⊥BC于M,DN⊥AC于点N,
∴DM=DN.
∵,,
∴S△ACD:S△BCD=AC:BC=3:2.
∵AB=AC,AE⊥BC,
∴BE=CE=.
∴CE:AC=1:3.
∴cos∠ACB=.
故答案为:.
12.解:如图,过A作AH⊥BC,交CB的延长线于点H,
在Rt△ACD中,
∵∠CAD=30°,AD=150m,
∴CD=AD tan30°=150×=50(m),
∴AH=CD=50m.
在Rt△ABH中,
∵∠BAH=30°,AH=50m,
∴BH=AH tan30°=50×=50(m),
∴BC=AD﹣BH=150﹣50=100(m),
答:这栋楼的高度为100m.
故答案为:100.
13.解:(1)如图,过点B作BM⊥AE,BN⊥CE,垂足分别为M、N,
由题意可知,∠CBN=45°,∠DAE=53°,i=1:,AB=10米,AE=21米.
∵i=1:==tan∠BAM,
∴∠BAM=30°,
∴BM=AB=5(米),
即点B距水平地面AE的高度为5米;
(2)在Rt△ABM中,∠BAM=30°,
∴BM=AB=5(米)=NE,AM=AB=5(米),
∴ME=AM+AE=(5+21)米=BN,
∵∠CBN=45°,
∴CN=BN=ME=(5+21)米,
∴CE=CN+NE=(5+26)米,
在Rt△ADE中,∠DAE=53°,AE=21米,
∴DE=AE tan53°≈21×=28(米),
∴CD=CE﹣DE=5+26﹣28=5﹣2≈6.7(米),
即广告牌CD的高度约为6.7米.
14.解:设BC=x米,则AC=(x+5)米,
在Rt△BDC中,∠BDC=45°,
∴DC=BC=x米,
在Rt△ADC中,tan∠ADC=,即=1.2,
解得:x=25,
答:建筑物BC的高度为25米.
15.解:设OC=x海里,
依题意得∠OAB=30°,∠OBC=∠BOC=45°,作OC⊥AB,
∴BC=OC=x海里,AC=x海里,
∵AC﹣BC=10,
∴(﹣1)x=10,
解得x==5(+1),
答:船与小岛的距离是5(+1)海里.
16.解:过C作CD⊥AB于D,
则∠ACD=59°,∠DCB=45°,BD=6m,
在Rt△BCD中,∵∠BDC=90°,∠BCD=45°,
∴△BCD是等腰直角三角形,
∴BD=CD=6(m),
在Rt△ADC中,∠ADC=90°,∠ACD=59°,
∴tan59°=,
∴AD=CD tan59°≈6×1.67≈10(m),
∴AB=AD+BD=10+6=16(m),
答:旗杆AB的高约为16m.
17.解:在Rt△BCD中,BC=DC tan30°=12×=4(m),
在Rt△ACD中,AC=DC tan37°≈12×0.75=9(m),
∴AB=AC﹣BC=(9﹣4)(m).
答:广告牌AB的高度约为(9﹣4)m.
18.解:由已知得:∠ECA=29.5°,∠FCB=45°,CD=80米,EF∥AB,CD⊥AB,
∴∠A=∠ECA=29.5°,∠B=∠FCB=45°,
∴△BCD是等腰直角三角形,
∴BD=CD=80米,
在Rt△ACD中,∠CDA=90°,tanA=,
∴AD==≈140.4(米),
∴AB=AD+BD≈140.4+80≈220(米),
即建筑物A、B之间的距离约为220米.
19.解:在Rt△ABD中,tan∠BAD=,
∴BD=ADtan45°=50×1=50(m),
在Rt△ADC中,tan∠CAD=,
∴CD=ADtan60°=50×=50(m),
∴BC=BD+CD=(50+50)m,
答:这栋高楼的高度为(50+50)m.
20.解:过A点作AE⊥CD于E点,
由题意得,四边形ABDE为矩形,
∵∠DAE=26.6°,BD=30m,
∴AE=BD=30m,tan26.6°=,
∴DE=tan26.6° AE=0.50×30=15m,
∵∠CAE=45°,
∴∠ACE=45°,
∴AE=EC,
∴CE=30m,
∴CD=CE+ED=30+15=45(m),
∴建筑物CD的高度是45m.
21.解:过点 D作 DE⊥AC 交 AC于点 E,DF⊥AB交 AB于点 F,
∵i=1:3,CD=10,
设 DE=xm,则 CE=3xm,
在 Rt△CED 中,x2+(3x)2=102,
解得:x=或x=﹣(舍),
∴DE=m,则CE=3m,
∵∠BDF=∠DBF=45°,
∴BF=DF,
设 BF=DF=m 米,则 AB=(m+)米,AC=(m﹣3)米,
在 Rt△CAB 中,,
解得:m≈29.9,
∴AB=29.9+≈33.1(米),
答:塑像的高度约为 33.1米.
22.解:如图,过点A作AG⊥CD于G,设CD=x,
∴四边形ABDG是矩形,
∴AG=BD,GD=AB,
∵∠CED=53°,
∴DE=,
∴AG=BD=+2,
∵∠CAG=30°,
∴CG=AG tan30°,即CD﹣GD=AG tan30°,
∴,
解得:x≈20,
∴CF=CD﹣DF=20﹣8=12(米),
答:雕像CF的高为12米.
23.解:设AD=xm,
∵∠ABD=45°,
∴BD=AD=xm,
∵∠ACD=31°,BC=60m,
∴tan31°==≈0.60,
解得x=90.0,
∴他家到公路l的距离AD的长度约90.0m.
24.解:(1)作BD⊥AC于D.
依题意得,
∠BAE=45°,∠ABC=105°,∠CAE=15°,
∴∠BAC=30°,
∴∠ACB=45°.
在Rt△BCD中,∠BDC=90°,∠ACB=45°,
∴∠CBD=45°,
∴∠CBD=∠DCB,
∴BD=CD,
设BD=xkm,则CD=xkm,
在Rt△ABD中,∠BAC=30°,
∴AB=2BD=2xkm,tan30°=,
∴=,
∴AD=x,
在Rt△BDC中,∠BDC=90°,∠DCB=45°,
∴sin∠DCB==,
∴BC=x,
∵CD+AD=30+30,
∴x+x=30+30,
∴x=30,
∴AB=2x=60(km);
(2)第二组先到达目的地,
理由:∵BD=30km,
∴BC=x=30km,
第一组用时:60÷40=1.5(h);第二组用时:30÷35=(h),
∵<1.5,
∴第二组先到达目的地,
答:第二组先到达目的地.
25.解:(1)在Rt△ADE中,∠AED=90°,AE=6,cosA=,
∴AD==10,
∴==8.
∵BD平分∠ABC,DE⊥AB,DC⊥BC,
∴CD=DE=8;
(2)由(1)AD=10,DC=8,
∴AC=AD+DC=18,
在△ADE与△ABC中,
∵∠A=∠A,∠AED=∠ACB,
∴△ADE∽△ABC,
∴,即=,
∴BC=24,
∴.
26.解:(1)过点B作BM⊥AC于点M,如图所示:
由题意,知∠BAM=45°,则∠ABM=45°.
在Rt△ABM中,∠BAM=45°,AB=80nmile,
∴△ABM是等腰直角三角形,
∴BM=AM=AB=40(nmile)
答:渔船航行40nmile与小岛B的距离最近.
(2)∵BM=40nmile,MC=40nmile,
∴,
∴∠MBC=60°,
∴∠CBG=180°﹣60°﹣45°﹣30°=45°,
在Rt△BCM中,∠MBC=60°,
∴∠BCM=30°,
∴BC=2BM=80(nmile),
答:救援队从B处出发沿着点B的南偏东45°方向航行到达事故地点航程最短,最短航程是80nmile.
